Approximation de π
Dans l'histoire des mathématiques, les approximations de la constante π ont atteint une précision de 0,04 % de la valeur réelle avant le début de l'ère commune (Archimède). Au Ve siècle, des mathématiciens chinois les ont améliorées jusqu'à sept décimales.

De grandes avancées supplémentaires n'ont été réalisées qu'à partir du XVe siècle (Al-Kashi). Les premiers mathématiciens modernes ont atteint une précision de 35 décimales au début du XVIIe siècle (Ludolph van Ceulen) et 126 chiffres au XIXe siècle (Jurij Vega), dépassant la précision requise pour toute application concevable en dehors des mathématiques pures.
Le record de l'approximation manuelle de π est détenu par William Shanks, qui a calculé 527 décimales correctes vers 1873. Depuis le milieu du XXe siècle, l'approximation de π est effectuée sur ordinateurs par des logiciels spécifiques.
Le le record est établi avec 62,8 billions de décimales par Thomas Keller et Heiko Rölke de la Haute école des sciences appliquées (de) des Grisons en Suisse.
Histoire
Antiquité
Les approximations les plus connues de π datant avant l'ère commune étaient exactes à deux décimales ; cela a été amélioré avec les mathématiques chinoises en particulier au milieu du premier millénaire, à une précision de sept décimales. Après cela, aucun progrès n'a été réalisé jusqu'à la fin de la période médiévale.[pas clair]
Les mathématiques babyloniennes évaluaient généralement π à 3, ce qui suffisait pour les projets architecturaux de l'époque (notamment dans la description du temple de Salomon dans la Bible hébraïque)[1]. Les Babyloniens savaient qu'il s'agissait d'une approximation, et une vieille tablette mathématique babylonienne exhumée près de Suse en 1936 (datée entre le XIXe et le XVIIe siècle avant notre ère) apporte une meilleure approximation de π, 25⁄8 = 3,125, soit proche de 0,5% de la valeur exacte[2],[3],[4],[5].
À peu près au même moment, le papyrus Rhind (daté de la Deuxième Période intermédiaire égyptienne, soit 1600 avant notre ère) donne l'approximation 256⁄81 ≈ 3,16 (précis à 0,6 %) en calculant l'aire d'un octogone régulier approximant un cercle[6].
Les calculs astronomiques dans le Shatapatha Brahmana (vers le VIe siècle avant notre ère) utilisent l'approximation fractionnaire 339/108 ≈ 3,139[7].
Au IIIe siècle avant notre ère, Archimède a prouvé les inégalités strictes 223⁄71 < π < 22⁄7, au moyen d'un 96-gone (précision de 2 × 10−4 et 4 × 10−4, respectivement). Il est possible de prouver que 22 / 7 dépasse π grâce à un calcul d'intégrales élémentaire[précision nécessaire], mais cette technique n'existait pas à l'époque d'Archimède.
Au IIe siècle, Ptolémée a utilisé la valeur 377⁄120, la première approximation connue précise à trois décimales[8].
Le mathématicien chinois Liu Hui, en 263, a calculé que π serait compris entre 3,141024 et 3,142708, valeurs correspondant respectivement aux constructions d'un 96-gone et d'un 192-gone ; la moyenne de ces deux valeurs est 3,141866 (précision de 9 × 10−5). Il a également suggéré que 3,14 était une approximation suffisante pour des applications pratiques. Il a souvent été crédité d'un résultat plus précis π ≈ 3927/1250 = 3,1416 (précision de 2 × 10−6), bien que certains chercheurs pensent plutôt que celui-ci est dû au mathématicien chinois Zu Chongzhi[9]. Zu Chongzhi est connu pour avoir donné l'encadrement de π entre 3,1415926 et 3,1415927, correct à sept décimales près. Il a donné deux autres approximations de π : π ≈ 22/7 et π ≈ 355/113. La dernière fraction est la meilleure approximation rationnelle possible de π en utilisant moins de cinq chiffres décimaux au numérateur et au dénominateur. Le résultat de Zu Chongzhi restera l'approximation la plus juste pendant près d'un millénaire.
À l'époque de l'empire Gupta (VIe siècle), le mathématicien Aryabhata, dans son traité astronomique Āryabhaṭīya, a calculé la valeur de π à cinq chiffres significatifs (π ≈ 62832/20000 = 3,1416)[10]. Il l'a utilisée pour calculer une approximation de la circonférence de la Terre[11]. Aryabhata a affirmé que son résultat donnait « approximativement » (āsanna) la circonférence d'un cercle. Nilakantha Somayaji (école du Kerala) a fait remarquer, au XVe siècle, que le mot signifie non seulement que c'est une approximation, mais que la valeur est « incommensurable » (c.-à-d. irrationnelle)[12].
Moyen Âge
Au Ve siècle, π était connu à environ sept décimales dans les mathématiques chinoises, et à environ cinq dans les mathématiques indiennes. Les progrès suivants n'ont été réalisés que plus d'un millénaire après, au XIVe siècle, lorsque le mathématicien et astronome indien Madhava de Sangamagrama, fondateur de l'école du Kerala d'astronomie et de mathématiques, a découvert une série infinie pour π, maintenant connue sous le nom de formule de Madhava-Leibniz[13],[14], et a donné deux méthodes pour calculer la valeur de π. Ce faisant, il a obtenu la série infinie
et a utilisé les 21 premiers termes pour calculer les 11 premières décimales de π.
L'autre méthode qu'il utilisait était d'ajouter un terme restant à la série originale de π. Il a utilisé le terme restant
dans l'extension de série infinie de π⁄4 pour améliorer l'approximation de π à 13 décimales, lorsque n = 75.
En 1424, Al-Kashi, un astronome et mathématicien perse, a calculé correctement 2π à 9 chiffres sexagésimaux[15]. Convertie en base dix, cette approximation est donnée par 17 chiffres :
- ,
ce qui équivaut à
- .
Il a atteint ce niveau de précision en calculant le périmètre d'un polygone régulier à 3 × 228 côtés[16].
Du XVIe au XIXe siècle
Dans la seconde moitié du XVIe siècle, le mathématicien français François Viète a découvert un produit infini qui converge vers π, connu sous le nom de formule de Viète.
Le mathématicien germano-néerlandais Ludolph van Ceulen (vers 1600) a calculé les 35 premières décimales de π à l'aide d'un 262-gone. Il était si fier de ce résultat qu'il l'a fait inscrire sur sa pierre tombale.
Dans Cyclometricus (1621), Willebrord Snell affirme que le périmètre du polygone inscrit approche la circonférence deux fois plus vite que le périmètre du polygone circonscrit correspondant. La preuve sera apportée par Christiaan Huygens en 1654. Snell a obtenu 7 décimales de π avec un 96-gone (en)[17].
En 1789, le mathématicien slovène Jurij Vega a calculé les 140 premières décimales de π, cependant les 14 dernières étaient incorrectes[18] ; ce résultat a néanmoins été le record du monde pendant 52 ans, jusqu'en 1841, lorsque William Rutherford (en) a calculé 208 décimales dont les 152 premières étaient correctes. Vega a ensuite amélioré la formule de John Machin à partir de 1706 et sa méthode est encore mentionnée aujourd'hui.
Le mathématicien amateur anglais William Shanks a passé plus de 20 ans à calculer les 707 premières décimales de π. Lorsqu'il eut terminé sa tâche en 1873, les 527 premières décimales étaient correctes. Il calculait de nouvelles décimales toute la matinée et passait l'après-midi à vérifier le travail de la matinée. Il s'agissait de l'approximation la plus précise de π jusqu'à l'avènement de l'ordinateur, un siècle plus tard.
XXe siècle
En 1910, le mathématicien indien Srinivasa Ramanujan a trouvé plusieurs séries infinies de π à convergence rapide, comme
qui calcule à chaque nouvelle itération huit décimales supplémentaires de π. Ses séries sont maintenant la base des algorithmes les plus rapides actuellement utilisés pour calculer π.
À partir du milieu du XXe siècle, tous les calculs de π ont été effectués à l'aide de calculatrices ou d'ordinateurs.
En 1944, D. F. Ferguson, à l'aide d'une calculatrice mécanique, a constaté que William Shanks avait commis une erreur à la 528e décimale et que toutes les décimales suivantes étaient incorrectes.
Dans les premières années de l'ordinateur, un développement de π à 100 000 décimales[19] a été calculé par le mathématicien de l'université du Maryland Daniel Shanks (n'ayant aucun rapport avec William Shanks mentionné ci-dessus) et son équipe au Naval Research Laboratory à Washington. En 1961, Shanks et son équipe ont utilisé deux séries différentes pour calculer les décimales de π. Pour l'une, on savait que toute erreur produirait une valeur légèrement trop élevée, et pour l'autre, on savait que toute erreur produirait une valeur légèrement trop faible par rapport à la valeur réelle ; par conséquent, tant que les deux séries produisaient les mêmes chiffres, il n'y avait pratiquement aucun doute sur la justesse des décimales calculées. Les premiers 100 265 chiffres après la virgule de π ont été publiés en 1962[19].
En 1989, les frères Chudnovsky ont calculé correctement π à 4,8 × 108 décimales grâce au superordinateur IBM 3090 en utilisant la variation suivante de la série infinie de Ramanujan :
- .
En 1999, Yasumasa Kanada et son équipe de l'université de Tokyo ont calculé π à 2,061 584 3 × 1011 décimales, grâce au superordinateur Hitachi SR8000/MPP en utilisant une autre variante de la série infinie de Ramanujan.
XXIe siècle
Les records depuis lors ont tous été accomplis sur des ordinateurs personnels[Passage contradictoire] en utilisant l'algorithme de Chudnovsky (en).
Le 6 décembre 2002, Yasumasa Kanada et une équipe de 9 autres personnes, utilisant le Hitachi SR8000, un supercalculateur avec 1 téraoctet de mémoire, ont calculé π à environ 1,241 1 × 1012 décimales en environ 600 heures[20],[21].
Le 29 avril 2009, Daisuke Takahashi et al., de l'université de Tsukuba, avec un supercalculateur T2K, ont plus que doublé le record précédent, en calculant π à plus de 2,57 × 1012 décimales, en moins de 74 heures au total (calcul et vérification)[22].
Le 31 décembre 2009, Fabrice Bellard a utilisé un ordinateur personnel pour calculer un peu moins de 2,7 × 1012 décimales de π. Les calculs ont été effectués en binaire, puis le résultat a été converti en base 10. Les étapes de calcul, de conversion et de vérification ont pris au total 131 jours[23].
De 2010 à 2020, tous les records ont été obtenus à l'aide du logiciel « y-cruncher » d'Alexander Yee :
- En août 2010, Shigeru Kondo a calculé 5 × 1012 décimales de π[24]. Le calcul a été effectué entre le 4 mai et le 3 août, les vérifications primaires et secondaires ayant respectivement duré 64 et 66 heures[25].
- Le 16 octobre 2011, Shigeru Kondo a doublé son propre record en calculant 1013 décimales en utilisant la même méthode, mais assisté d'un meilleur matériel[26],[27],[28].
- En décembre 2013, Kondo a battu son propre record pour la seconde fois lorsqu'il a calculé 1,21 × 1013 décimales de π. La limitation était principalement due à l'espace de stockage[29].
- Le 8 octobre 2014, un individu non identifié, connu sous le pseudonyme de « houkouonchi », a calculé 1,33 × 1013 décimales de π[30].
- Le 15 novembre 2016, Peter Trueb et ses sponsors ont calculé, toujours grâce au programme y-cruncher, 2,245 915 771 836 1 × 1013 (πe × 1012) décimales de π. Le calcul a pris (avec 3 interruptions) 105 jours[30],[31].
- Le 14 mars 2019, Google, en la personne d'Emma Haruka Iwao, rend public[32] le nouveau record qui s'établit à 31 415 926 535 897 (la partie entière de π e13) décimales de π.
- Le 29 janvier 2020 un nouveau record est établi avec 50 billions de décimales ( 50 000 000 000 000 ) par Timothy Mullican[33],[34], après 303 jours de calcul[35].
Le un nouveau record est établi avec 62,8 billions de décimales par Thomas Keller et Heiko Rölke de la Haute école des sciences appliquées (de) des Grisons en Suisse[36]. Le temps de calcul a été d'un peu plus de 108 jours.
Développement de formules efficaces
Approximation polygonale d'un cercle
Archimède, dans De la mesure du cercle, a créé le premier algorithme pour le calcul de π, basé sur l'idée que le périmètre de n'importe quel polygone inscrit dans un cercle est inférieur à la circonférence du cercle qui, à son tour, est inférieur au périmètre de tout polygone circonscrit à ce cercle. Il a commencé par des hexagones réguliers inscrits et circonscrits, dont les périmètres sont facilement déterminés. Il montre alors comment calculer les périmètres des polygones réguliers ayant deux fois plus de côtés qui sont inscrits et circonscrits autour du même cercle. Il s'agit d'une procédure récursive qui serait décrite aujourd'hui comme suit :
Soit pk et Pk les périmètres de polygones réguliers à k côtés, inscrits et circonscrits autour du même cercle, respectivement. Alors,
Archimède a utilisé le processus décrit pour calculer successivement P12, p12, P24, p24, P48, p48, P96 et p96[37]. Il a obtenu l'encadrement suivant en partant des trois dernières valeurs
- .
On ne sait pas pourquoi Archimède s'est arrêté à un polygone de 96 côtés. Héron rapporte dans son Metrica qu'Archimède a continué le calcul dans un livre maintenant perdu, mais lui attribue une valeur incorrecte[38].
Archimède n'a pas utilisé la trigonométrie dans ce calcul et la difficulté d'appliquer la méthode réside dans l'obtention de bonnes approximations pour les racines carrées des calculs impliqués. La trigonométrie a probablement été utilisée par Claudius Ptolémée pour obtenir la valeur de π donnée dans l'Almageste (environ 150 après J.C.)[39].
La formule de Viète, publiée par François Viète en 1593, a été obtenue en utilisant une méthode polygonale, avec des aires (plutôt que des périmètres) de polygones dont les nombres de côtés sont des puissances de 2[40].
Une amélioration trigonométrique par Willebrord Snell (1621) a permis d'obtenir de meilleures limites à partir de la méthode du polygone. Ainsi, des résultats plus précis ont été obtenus, nécessitant moins de côtés[41]. La dernière tentative majeure de calculer π par cette méthode a été effectuée en 1630 par Christopher Grienberger, qui a calculé 39 décimales en utilisant l'amélioration de Snell.
Formules du type de Machin
Pour des calculs rapides, on peut utiliser des formules similaires à celle de John Machin :
avec le développement en série de Taylor de la fonction arc tangente. Cette formule se vérifie plus facilement à l'aide de coordonnées polaires de nombres complexes, produisant :
- .
((x, y) = (239, 132) est une solution de l'équation de Pell x2 − 2y2 = −1.)
Les formules de ce type sont connues sous le nom de formules du type de Machin. Elles ont bien été utilisées dans l'ère informatique pour calculer un nombre record de décimales de π mais plus récemment, d'autres formules similaires ont été utilisées.
Par exemple, Shanks et son équipe ont utilisé la formule suivante de Machin en 1961 pour calculer les 100 000 premiers chiffres de π :
- ,
ainsi que
- ,
servant de vérification.
Le record enregistré en décembre 2002 par Yasumasa Kanada (voir supra) utilisait les formules suivantes de Machin :
K. Takano (1982).
F. C. W. Störmer (1896).
Autres formules classiques
D'autres formules qui ont été utilisées pour calculer les estimations de π sont entre autres :
Liu Hui (voir aussi Formule de Viète) :
Madhava :
Euler :
Transformation de Newton/Euler[42] :
où (2k + 1)!! désigne le produit des entiers impairs jusqu'à 2k + 1.
Le travail de Ramanujan est à la base de l'algorithme de Chudnovsky, les algorithmes les plus rapides utilisés pour calculer π.
Algorithmes modernes
Les développements décimaux extrêmement longs de π sont généralement calculés avec des algorithmes tels que l'algorithme de Gauss-Legendre et l'algorithme de Borwein (en). Ce dernier, trouvé en 1985 par Jonathan et Peter Borwein, converge très rapidement :
Pour et
où , la suite converge de manière quartique vers π et donne 171 décimales en trois étapes[43], donc plus de 1012 décimales en 20 étapes. Cependant, l'algorithme de Chudnovsky (qui converge linéairement) est plus rapide que ces formules itératives.
Le premier million de décimales de π et 1/π sont disponibles grâce au projet Gutenberg (voir les liens externes ci-dessous).
Approximations diverses
Historiquement, la base 60 a été utilisée pour les calculs de π. Dans cette base, π peut être approché à huit chiffres (décimaux) significatifs avec le nombre 3:8:29:44_60, c'est-à-dire :
(Le chiffre sexagésimal suivant est 0, ce qui permet de tronquer ici pour obtenir une approximation relativement bonne.)
En outre, les expressions suivantes peuvent être utilisées pour estimer π :
- précision de trois décimales :
- précision de trois décimales :
- Karl Popper a spéculé[44] sur l'hypothèse que cette approximation, mentionnée par Émile Borel[45], aurait pu avoir déjà été remarquée par Platon.
- précision de quatre décimales:
- précision de quatre décimales :
- une approximation par Ramanujan, précise à 4 chiffres :
- précision de cinq décimales :
- précision de neuf décimales :
Provenant de Ramanujan, celui-ci a affirmé que la déesse de Namagiri lui était apparue dans un rêve et lui avait dit la vraie valeur de π[48].
- précision de dix décimales :
- précision de dix décimales :
Cette approximation curieuse résulte de l'observation que la 193e puissance de 1/π, produisant la suite 1122211125[49]...[précision nécessaire]
- précision de 18 décimales :
- précision à 30 chiffres :
- Dérivé du nombre de Heegner 640320³+744. Cette méthode n'admet pas de généralisations évidentes, car il n'y a qu'un nombre fini de nombres de Heegner.
- précision de 52 décimales :
- Comme celui ci-dessus, une conséquence du j-invariant.
- précision de 161 décimales :
- où u est un produit de quatre unités quartiques,
- et
- .
- Méthode basée sur le travail de Daniel Shanks. Semblable aux deux précédentes, mais qui est cette fois un quotient de forme modulaire, à savoir la fonction êta de Dedekind, et où l'argument implique .
- La fraction continue de π peut être utilisée pour générer des approximations rationnelles successives. Ce sont les meilleures approximations rationnelles possibles de π par rapport à la taille de leurs dénominateurs. Voici une liste des treize premières fractions :
- .
Approximation de l'aire d'un disque par quadrillage
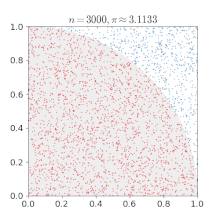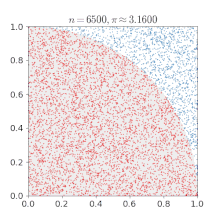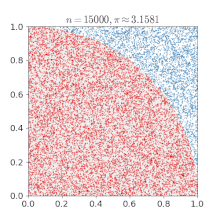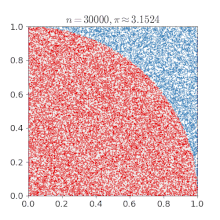
π peut être obtenu à partir d'un cercle, si son rayon et son aire sont connus, en utilisant la relation :
- .
Si on considère un cercle de rayon r avec son centre situé en (0, 0), tout point dont la distance à l'origine est inférieure à r sera situé dans le disque. Le théorème de Pythagore donne la distance de n'importe quel point (x, y) au centre :
Les carrés dont le centre se trouve à l'intérieur ou exactement à la limite du cercle peuvent ensuite être comptés en testant si, pour chaque point (x, y),
Le nombre total de point satisfaisant cette condition se rapproche ainsi de l'aire du cercle, qui peut ensuite être utilisée pour calculer une approximation de π.
Cette formule s'écrit :
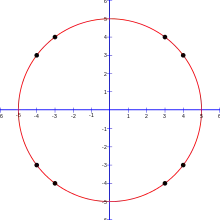
Autrement dit, on commence par choisir une valeur pour r. En considérant tous les points (x, y) dans lesquels x et y sont des entiers compris entre −r et r. Il suffit alors de diviser la somme représentant l'aire d'un cercle de rayon r, par r2 pour trouver une approximation de π. Par exemple, si r est égal à 5, alors les points considérés sont :
| (−5,5) | (−4,5) | (−3,5) | (−2,5) | (−1,5) | (0,5) | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) |
| (−5,4) | (−4,4) | (−3,4) | (−2,4) | (−1,4) | (0,4) | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) |
| (−5,3) | (−4,3) | (−3,3) | (−2,3) | (−1,3) | (0,3) | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) |
| (−5,2) | (−4,2) | (−3,2) | (−2,2) | (−1,2) | (0,2) | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) |
| (−5,1) | (−4,1) | (−3,1) | (−2,1) | (−1,1) | (0,1) | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) |
| (−5,0) | (−4,0) | (−3,0) | (−2,0) | (−1,0) | (0,0) | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) |
| (−5,−1) | (−4,−1) | (−3,−1) | (−2,−1) | (−1,−1) | (0,−1) | (1,−1) | (2,−1) | (3,−1) | (4,−1) | (5,−1) |
| (−5,−2) | (−4,−2) | (−3,−2) | (−2,−2) | (−1,−2) | (0,−2) | (1,−2) | (2,−2) | (3,−2) | (4,−2) | (5,−2) |
| (−5,−3) | (−4,−3) | (−3,−3) | (−2,−3) | (−1,−3) | (0,−3) | (1,−3) | (2,−3) | (3,−3) | (4,−3) | (5,−3) |
| (−5,−4) | (−4,−4) | (−3,−4) | (−2,−4) | (−1,−4) | (0,−4) | (1,−4) | (2,−4) | (3,−4) | (4,−4) | (5,−4) |
| (−5,−5) | (−4,−5) | (−3,−5) | (−2,−5) | (−1,−5) | (0,−5) | (1,−5) | (2,−5) | (3,−5) | (4,−5) | (5,−5) |
Les 12 points (0, ±5), (±5, 0), (±3, ±4), (±4, ±3) sont exactement sur le cercle, tandis que 69 points sont à l'intérieur. Par conséquent, l'aire est 81, et π est approximé à environ 3,24 car 81/52 = 3,24. Les résultats pour certaines valeurs de r sont présentés dans le tableau ci-dessous :
| r | Aire | Approximation de π |
|---|---|---|
| 2 | 13 | 3,25 |
| 3 | 29 | 3,22222 |
| 4 | 49 | 3,0625 |
| 5 | 81 | 3,24 |
| 10 | 317 | 3,17 |
| 20 | 1257 | 3,1425 |
| 100 | 31417 | 3,1417 |
| 1000 | 3141549 | 3,141549 |
Fractions continues
π a de nombreuses représentations en fraction continue généralisée générées par une règle simple :
- [51].
Série de Gregory-Leibniz
est la série de puissance pour arctan(x) en posant x = 1. Elle converge trop lentement pour avoir un intérêt pratique.
Arcsinus 1
Sachant que arcsin(1) = π/2, le développement en série entière de arc sin peut être simplifié pour obtenir :
- ,
mais avec une convergence presque aussi lente que la précédente (10 termes supplémentaires donnent trois décimales de plus).
Arcsinus 1/2
En notant que
nous avons
avec une convergence telle que chaque cinq termes supplémentaires donne au moins trois décimales de plus.
Calcul de la n-ième décimale de π
La formule Bailey-Borwein-Plouffe (BBP) pour calculer π a été découverte en 1995 par Simon Plouffe. En utilisant le système hexadécimal, la formule peut calculer n'importe quelle décimale de π sans avoir à calculer les décimales situées avant elle.
- .
En 1996, Simon Plouffe en a déduit un algorithme pour extraire le n-ième chiffre décimal de π, en base 10, en un temps de calcul amélioré d'un facteur O(n3(log n)3). L'algorithme ne nécessite presque aucune mémoire de stockage[52].
- .
Le temps de calcul de la formule de Plouffe a été amélioré de O(n2) par Fabrice Bellard, qui a démontré une formule alternative pour calculer π[53].
- .
Logiciels pour calculer π
Au cours des années, plusieurs logiciels ont été écrits pour calculer π sur les ordinateurs personnels. Ils impliquent généralement une vérification et un échange de disque efficace pour faciliter des calculs extrêmement coûteux en ressources.
- Super PI par Kanada Laboratory à l'université de Tokyo. Il pouvait calculer un million de chiffres en 40 minutes, deux millions de chiffres en 90 minutes et quatre millions de chiffres en 220 minutes sur un Pentium 90 MHz.
- PiFast par Xavier Gourdon était le programme le plus rapide sous Windows en 2003. Selon son auteur, il peut calculer un million de décimales en 3,5 secondes sur un Pentium de 2.4 GHz (ordinateur personnel haut-de-gamme à l'époque). PiFast peut également calculer d'autres nombres irrationnels comme e et .
- QuickPi par Steve Pagliarulo. Comme PiFast, QuickPi peut également calculer d'autres nombres irrationnels comme ou . Le logiciel est disponible sur Stu's Pi.
- y-cruncher[54] par Alexander Yee est le programme que Shigeru Kondo a utilisé pour calculer le record mondial de 2020 du nombre de décimales et qui a été utilisé pour la plupart des records subséquents. y-cruncher peut également être utilisé pour calculer d'autres constantes, et atteindre des records mondiaux pour plusieurs d'entre elles.
Notes et références
- Voir en:Approximations of π#Imputed biblical value.
- (en) David Gilman Romano, Athletics and Mathematics in Archaic Corinth: The Origins of the Greek Stadion, American Philosophical Society, 1993, p. 78, aperçu sur Google Livres.
- E. M. Bruins, Quelques textes mathématiques de la Mission de Suse, 1950.
- E. M. Bruins and M. Rutten, « Textes mathématiques de Suse », Mémoires de la Mission archéologique en Iran, vol. XXXIV, 1961.
- Voir aussi Beckmann 1971, p. 12, 21-22 « in 1936, a tablet was excavated some 200 miles from Babylon ».
- (en) Victor J. Katz (ed.), Annette Imhausen et al., The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, 2007 (ISBN 978-0-691-11485-9).
- (en) Krishna Chaitanya, A Profile of Indian Culture, Indian Book Company, 1975, p. 133.
- (en) Lazarus Mudehwe, « The story of pi ».
- (en) Lay Yong Lam et Tian Se Ang, « Circle measurements in ancient China », Historia Mathematica, vol. 13, no 4, , p. 325-340 (DOI 10.1016/0315-0860(86)90055-8, Math Reviews 875525).
- Āryabhaṭīya (gaṇitapāda 10), cité et traduit dans (en) Harold R. Jacobs, Geometry: Seeing, Doing, Understanding, 2003 (3e éd.), New York, W. H. Freeman and Company, p. 70.
- (en) John J. O'Connor et Edmund F. Robertson, « Aryabhata the Elder », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne).
- (en) S. Balachandra Rao, Indian Mathematics and Astronomy : Some Landmarks, Bangalore, Jnana Deep Publications, , 207 p. (ISBN 978-81-7371-205-0)
- (en) George E. Andrews et Richard Askey, Special Functions, Cambridge University Press, , 682 p. (ISBN 978-0-521-78988-2), p. 58.
- (en) R. C. Gupta, « On the remainder term in the Madhava–Leibniz's series », Ganita Bharati, vol. 14, nos 1-4, , p. 68-71.
- Al-Kashi, author: Adolf P. Youschkevitch, chief editor: Boris A. Rosenfeld, p. 256
- (en) Mohammad K. Azarian, « al-Risāla al-muhītīyya: A Summary », Missouri Journal of Mathematical Sciences, vol. 22, no 2, , p. 64-85 (lire en ligne).
- http://www.ijpam.eu/contents/2003-7-2/4/4.pdf
- (en) Edward Sandifer, « Why 140 Digits of Pi Matter », dans Jurij baron Vega in njegov čas: Zbornik ob 250-letnici rojstva, Ljubljana, DMFA, (ISBN 978-961-6137-98-0, OCLC 448882242, LCCN 2008467244, lire en ligne), p. 17 : « We should note that Vega's value contains an error in the 127th digit. Vega gives a 4 where there should be an, and all digits after that are incorrect. »
- (en) D. Shanks et J. W. Wrench, Jr. (en), « Calculation of π to 100,000 decimals », Math. Comp., vol. 16, no 77, , p. 76-99 (DOI 10.2307/2003813, JSTOR 2003813) (p. 80-99).
- (en) « Announcement », sur super-computing.org (Kanada Laboratory).
- (en) David H. Bailey, « Some Background on Kanada's Recent Pi Calculation », .
- (en) Daisuke Takahashi, « Declared record: 2,576,980,370,000 decimal digits », .
- (en) Fabrice Bellard, « Pi Computation Record ».
- (en) « McCormick Grad Sets New Pi Record » (version du 28 septembre 2011 sur l'Internet Archive), .
- (en) Alexander J. Yee et Shigeru Kondo, « 5 Trillion Digits of Pi - New World Record », .
- By Glenn, « Short Sharp Science: Epic pi quest sets 10 trillion digit record », Newscientist.com, (consulté le )
- (en) Alexander J. Yee et Shigeru Kondo, « Round 2... 10 Trillion Digits of Pi », .
- « Le nombre Pi : Historique du record de décimales », sur www.math93.com.
- (en) Alexander J. Yee et Shigeru Kondo, « 12.1 Trillion Digits of Pi, And we're out of disk space... », .
- (en) Alexander J. Yee, « y-cruncher: A Multi-Threaded Pi Program », sur www.numberworld.org, .
- (en) Peter Treub « Digit Statistics of the First 22.4 Trillion Decimal Digits of Pi », .
- « Google explose le record de calcul de décimales de pi », .
- (en-GB) « Most accurate value of pi », sur Guinness World Records (consulté le )
- (en-US) Timothy Mullican, « Calculating Pi: My attempt at breaking the Pi World Record », sur Bits and Bytes, (consulté le )
- (en) « y-cruncher - A Multi-Threaded Pi-Program », sur y-cruncher, (consulté le )
- Un nouveau record de calcul du nombre Pi établit en Suisse. RTS Info, 16 aout 2021. Lire en ligne
- Eves 1992, p. 131.
- Beckmann 1971, p. 66.
- Eves 1992, p. 118.
- Beckmann 1971, p. 94-95.
- Eves 1992, p. 119.
- (en) Eric W. Weisstein, « Pi Formulas », sur MathWorld.
- (en) Ronald Mak, Java Number Cruncher : The Java Programmer's Guide to Numerical Computing, Prentice Hall, (lire en ligne), p. 353.
- (en) The Open Society and Its Enemies, 1945, Notes on chapter six sur Google Livres.
- L'Espace et le temps, 1922, Note III, § 6, aperçu sur Google Livres de la traduction en anglais.
- (en) Martin Gardner, New Mathematical Diversions, MAA, , p. 92.
- (en) Martin Schneider, « A nested radical approximation for π » (version du 6 juillet 2011 sur l'Internet Archive).
- Cahiers de Ramanujan, p. 16.[réf. incomplète][réf. à confirmer]
- Suite
 A271452 de l'OEIS.
A271452 de l'OEIS. - (en) Cetin Hakimoglu, « Mathematics », sur Seeking Alpha.
- D'autres représentations sont disponibles dans la section « Fractions continues » de l'article sur π.
- (en) Simon Plouffe, On the computation of the n'th decimal digit of various transcendental numbers, November 1996; Revised December 2009.
- (en) Site web de Fabrice Bellard: Bellard.org.
- (en) Alexander J. Yee, « y-cruncher - A Multi-Threaded Pi-Program »
Voir aussi
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) David H. Bailey, Peter B. Borwein et Simon Plouffe, « On the Rapid Computation of Various Polylogarithmic Constants », Math. Comp., vol. 66, no 218, , p. 903-913 (DOI 10.1090/S0025-5718-97-00856-9, lire en ligne).
- (en) Petr Beckmann (en), A History of π (en), New York, St. Martin's Press (en), (ISBN 978-0-88029-418-8, Math Reviews 0449960).

- (en) Howard Eves, An Introduction to the History of Mathematics, Saunders College Publishing (en), , 6th éd. (ISBN 978-0-03-029558-4).

- (en) K. Jackson et J. Stamp, Pyramid : Beyond Imagination. Inside the Great Pyramid of Giza, Londres, BBC, .
- (en) George G. Joseph, The Crest of the Peacock : Non-European Roots of Mathematics, Londres, Penguin, (ISBN 978-0-14-027778-4).
Articles connexes
- Journée de pi
- Point de Feynman
- Chronologie du calcul de π (en)
Lien externe
(en) « PI Competition », sur The Contest Center (listes d'approximations de π et liens vers d'autres telles listes)
- Portail des mathématiques