On appelle composante connexe d’un point ${\displaystyle x\in E}$, ${\displaystyle E}$ espace topologique, la plus grande partie connexe de ${\displaystyle E}$ (au sens de l'inclusion) contenant ce point. On note ${\displaystyle C_{x}}$ cet ensemble. On appelle composantes connexes d’une partie de ${\displaystyle E}$ les composantes connexes des points de cette partie.

• ${\displaystyle \mathbb {R} ^{*}}$ a deux composantes connexes : ${\displaystyle \mathbb {R} _{+}^{*}}$ et ${\displaystyle \mathbb {R} _{-}^{*}}$.
• L'espace ${\displaystyle \mathrm {GL} _{n}(\mathbb {R} )}$ des matrices inversibles de taille ${\displaystyle n}$ admet deux composantes connexes, données par le signe du déterminant.
• Dans ${\displaystyle \mathbb {N} }$ et plus généralement dans tout espace discret, les composantes connexes sont les singletons.

• ${\displaystyle \mathbb {N} }$ est totalement discontinu.
• L'ensemble (triadique) de Cantor est totalement discontinu.

Dans un espace topologique ${\displaystyle E}$, la composante connexe d’un point quelconque est un ensemble fermé. La relation « y appartient à ${\displaystyle C_{x}}$ » définie une relation d'équivalence ${\displaystyle {\mathcal {R}}}$ dans ${\displaystyle E}$, donc les classes d'équivalences sont les composantes connexes de ${\displaystyle E}$. De plus, l'espace quotient ${\displaystyle E/{\mathcal {R}}}$ est totalement discontinu.

Dans un espace produit ${\displaystyle E=\prod _{i\in I}E_{i}}$, la composante connexe d’un point ${\displaystyle x}$ est le produit des composantes connexes des points ${\displaystyle x_{i}}$ dans les espaces ${\displaystyle E_{i}}$.

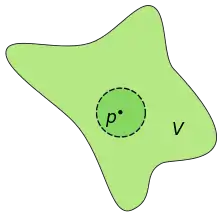
Un espace topologique ${\displaystyle E}$ est dit localement connexe si tout point de ${\displaystyle E}$ possède un système fondamental de voisinages connexes.

Soit ${\displaystyle E}$ un espace topologique. Les propositions suivantes sont équivalentes :

1. ${\displaystyle E}$ est localement connexe ;
2. pour tout ouvert ${\displaystyle U}$ de ${\displaystyle E}$, les composantes connexes de ${\displaystyle U}$ sont des ouverts de ${\displaystyle E}$ ;
3. les ouverts connexes forment une base d'ouverts de ${\displaystyle E}$.

• ${\displaystyle \mathbb {R} }$, ${\displaystyle \mathbb {C} }$, ${\displaystyle \mathbb {R} ^{n}}$ et plus généralement, tous les ${\displaystyle \mathbb {R} }$-espaces vectoriels normés, sont des espaces connexes et localement connexes.
• ${\displaystyle [0,1]\cup [2,3]}$ est localement connexe mais non connexe.
• On considère la partie ${\displaystyle A=(\{0\}\times \mathbb {R} )\cup (\mathbb {R} \times \mathbb {Q} )}$ de ${\displaystyle \mathbb {R} ^{2}}$. Elle est connexe mais non localement connexe : tout point de ${\displaystyle A}$ admet un voisinage connexe, à savoir ${\displaystyle A}$, mais non une base de voisinages connexes.
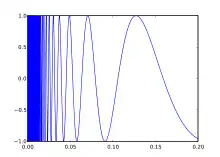
• Le graphe de la fonction ${\displaystyle x\mapsto \sin(1/x)}$ définie sur ${\displaystyle \mathbb {R} _{+}^{*}}$ est connexe mais non localement connexe.

Soit ${\displaystyle U}$ un ensemble ouvert d’un espace localement connexe ${\displaystyle E}$ et ${\displaystyle V}$ une composante connexe de ${\displaystyle U}$. Alors la frontière de ${\displaystyle V}$ est contenue dans la frontière de ${\displaystyle U}$.

• Tout quotient d’un espace localement connexe est localement connexe.
• Tout produit d'espaces localement connexes est localement connexe.

Soit ${\displaystyle E}$ un espace topologique et ${\displaystyle x}$, ${\displaystyle y}$ deux points de ${\displaystyle E}$. On appelle chemin d'origine ${\displaystyle x}$ et d'extrémité ${\displaystyle y}$ toute application continue ${\displaystyle \gamma$ :[0,1]\to E} telle que ${\displaystyle \gamma (0)=x}$ et ${\displaystyle \gamma (1)=y}$.

On dit que ${\displaystyle x}$ et ${\displaystyle y}$ sont reliés s'il existe un chemin d'origine ${\displaystyle x}$ et d'extrémité ${\displaystyle y}$ dans ${\displaystyle E}$.

La relation « x est relié à y » est une relation d'équivalence dans ${\displaystyle E}$.

Un espace topologique ${\displaystyle E}$ est dit connexe par arcs si tout couple de points de ${\displaystyle E}$ est relié par un chemin dans ${\displaystyle E}$.

Une partie A de E est dite connexe par arcs si tout couple de points de A est relié par un chemin restant dans A.

Soit E un espace vectoriel topologique réel (par exemple ${\displaystyle \mathbb {R} ^{n}}$).

• Si E est de dimension supérieure ou égale à 2 alors E* est connexe par arcs : on peut joindre x, y ∈ E* par le segment [x, y] si 0 ∉ ]x, y[ ou, si 0 ∈ ]x, y[, par la réunion de deux segments [x, z] et [z, y], en choisissant z ∉ (x0y).
• Tout convexe de E — ou plus généralement : toute partie étoilée, cf. définition ci-dessous — est connexe par arcs.

On dit qu'une partie ${\displaystyle {\mathcal {U}}}$ d'un espace vectoriel réel est étoilée depuis un pôle ${\displaystyle a\in {\mathcal {U}}}$ si :

${\displaystyle \forall x\in {\mathcal {U}}\quad [a,x]\subset {\mathcal {U}}}$.

Contrairement à la connexité, la connexité par arcs « ne passe pas aux adhérences ». Par exemple, le graphe de la fonction ${\displaystyle x\mapsto \sin(1/x)}$ (voir supra) est connexe par arcs mais son adhérence ne l'est pas (voir infra).

Soit ${\displaystyle X}$ un espace connexe. Si tout point de ${\displaystyle X}$ a un voisinage connexe par arcs, alors ${\displaystyle X}$ est connexe par arcs.

Dans un espace localement connexe par arcs, un ouvert est connexe (si et) seulement s'il est connexe par arcs.

On appelle composante connexe par arcs d'un point ${\displaystyle x}$ d'un espace topologique ${\displaystyle E}$, la classe de ${\displaystyle x}$ dans ${\displaystyle E}$ par la relation définie ci-dessus.

Voir les exercices sur : la connexité par arcs (Ex. 7).

L'adhérence du graphe de la fonction ${\displaystyle x\mapsto \sin(1/x)}$ (voir supra), munie de la topologie induite, admet deux « composantes connexes par arcs », à savoir le graphe et le segment ${\displaystyle \{(0,x)\mid x\in [-1,1]\}}$.