Théorème des valeurs intermédiaires
Soit une fonction continue sur un intervalle .
![{\displaystyle \left[a,b\right]}](../../I/f30926fb280a9fdf66fd931e14d4363cb824feaa.svg)
Pour tout réel compris entre et ,
il existe (au moins) un réel tel que .
![{\displaystyle c\in \left[a,b\right]}](../../I/b48d674e0c628e1da26f4ca2f6b1079842954555.svg)
Quitte à considérer et passer le problème à l'opposé, on peut supposer .
La méthode de dichotomie consiste à construire une suite d'intervalles In = [an, bn] tels que pour tout n :
- In+1 soit inclus dans In
- la longueur de In+1 soit la moitié de celle de In
- f(an) ≤ u ≤ f(bn).
On procède de la manière suivante :
- on pose initialement I0 = [a, b] ;
- quand, à un rang n, l'intervalle In est construit, on note mn son milieu et
- si f(mn) < u, on prend pour In+1 l'intervalle [mn, bn] et l'on pose an+1 = mn et bn+1 = bn ;
- si f(mn) ≥ u, on prend pour In+1 l'intervalle [an, mn] et l'on pose an+1 = an et bn+1 = mn.
Les suites (an) et (bn) sont alors adjacentes : en effet, la première est croissante (au sens large), la seconde est décroissante, et la différence entre les deux suites est égale à la longueur de In, soit (b – a)/2n qui tend vers 0.
Ces deux suites convergent donc vers une même limite c. Comme f est continue, les suites (f(an)) et (f(bn)) convergent vers f(c).
Comme, d'autre part, f(an) ≤ u pour tout n, on obtient f(c) ≤ u par passage à la limite.
Comme, enfin, f(bn) ≥ u pour tout n, on obtient f(c) ≥ u par passage à la limite.
Il en résulte que f(c) = u.
Pour montrer qu'une fonction continue s'annule sur ,
il suffit de montrer qu'elle change de signe sur .
Interprétation graphique
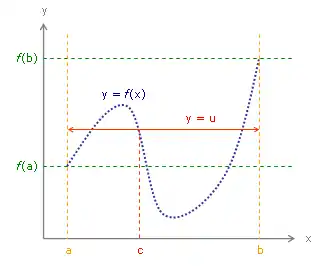
La droite d'équation coupe au moins une fois la courbe représentative de f.
Interprétation en termes d'équations
Soit f une fonction continue d'un intervalle I, a et b deux réels de I.
Pour tout réel u compris entre f(a) et f(b),
l'équation admet (au moins) une solution c comprise entre a et b. On peut démontrer l'unicité de cette solution si est strictement monotone sur et les conditions d'application du théorème.
Remarque : Le théorème des valeurs intermédiaires est un théorème d'existence qui ne précise pas la valeur des solutions.
Néanmoins des méthodes algorithmiques (comme la méthode de dichotomie) l'utilisent pour déterminer des valeurs approchées des solutions.