Vitesse de la lumière

La vitesse de la lumière dans le vide, communément notée c pour « célérité »[2],[3], est une constante physique universelle et un invariant relativiste (vitesse limite des théories relativistes), importante dans de nombreux domaines de la physique. Sa valeur exacte[alpha 1] est 299 792 458 m/s (environ 3 × 108 m/s ou 300 000 km/s). Selon la relativité restreinte, la vitesse de la lumière dans le vide est la vitesse maximale que peuvent atteindre toutes formes de matière ou d'information dans l'univers.

Vitesse de la lumière dans le vide
Unités SI mètre par seconde (m/s ou m s−1)
Autres unités CGS : centimètre par seconde (cm/s ou cm s−1)
Dimension
Nature Grandeur scalaire
Symbole usuel c
Valeur 299 792 458 m/s
Schéma représentant à l'échelle (spatiale et temporelle) le déplacement de la lumière entre la Terre et la Lune. La lumière met entre 1,2 et 1,35 seconde pour rejoindre la Lune (selon sa distance avec la Terre)[1].

Si cette vitesse est le plus souvent associée avec la lumière, elle définit plus largement la vitesse de toutes les particules sans masse et des variations de leurs champs associés dans le vide (y compris les rayonnements électromagnétiques et les ondes gravitationnelles). Ces particules et ondes voyagent à la vitesse c quel que soit le mouvement de la source émettrice ou le référentiel de l'observateur. Dans la théorie de la relativité, c permet de lier l'espace et le temps, et apparaît également dans la célèbre équation d'équivalence masse-énergie E = m c2[4].

La vitesse de la lumière n'est pas la même dans tous les milieux et se propage dans les matériaux transparents (tels que le verre, l'air, l'eau) à une vitesse inférieure à c. Le rapport de c sur v (vitesse dans un milieu) correspond à l'indice de réfraction n du milieu (n = c/v). Par exemple le verre a un indice de réfraction proche de 1,5, ce qui signifie que la lumière dans le verre se déplace à c/1,5 ≈ 200 000 km/s ; l'indice de réfraction de l'air pour la lumière visible est d'environ 1,0003, de sorte que la vitesse de la lumière dans l'air est d'environ 299 700 km/s.

Dans la vie de tous les jours, la lumière (et les autres ondes électromagnétiques) semble se propager instantanément, mais dans les calculs sur de longues distances sa vitesse entraîne des effets notables. Dans les communications avec des sondes spatiales par exemple, un message peut prendre de quelques minutes à quelques heures pour atteindre la sonde. De même, la lumière des étoiles a quitté ces astres depuis fort longtemps[alpha 2], de sorte que l'on peut étudier l'histoire de l'univers par l'observation de ces objets distants : « plus l'on regarde loin, plus l'on regarde dans le passé ». La vitesse finie de la lumière limite également la vitesse théorique maximale des ordinateurs, car l'information envoyée de puce à puce prend un temps fini incompressible.

En 1676, Ole Rømer est le premier à démontrer que la lumière voyage à une vitesse finie en observant le mouvement apparent et les émersions de la lune de Jupiter, Io. Malgré la rigueur de ses observations, de nombreux savants restent sceptiques quant à ce résultat. Par l'observation du phénomène d'aberration stellaire, dont on rend compte en tenant compte respectivement de la vitesse de la lumière d'une étoile observée et de la vitesse de rotation de la Terre autour du Soleil, James Bradley confirma néanmoins en 1729 le résultat de Rømer et parvint à en donner une valeur acceptable. En 1810, l'expérience du Français Arago démontre que la vitesse de la lumière est constante (toujours la même). En 1865, James Clerk Maxwell définit la lumière comme une onde électromagnétique, et sa vitesse de déplacement comme c (notation présente en premier dans sa théorie sur l'électromagnétisme)[5]. En 1905, Albert Einstein postule que la vitesse de la lumière, c, est, dans tout référentiel, une constante, et est indépendante du mouvement de la source de lumière[6]. Il explore les conséquences de ce postulat en décrivant la théorie de la relativité et, ce faisant, montre que le paramètre c est pertinent même en dehors des contextes de lumière et d'électromagnétisme.

Après des siècles d'amélioration des mesures, en 1975, la vitesse de la lumière est estimée à 299 792 458 m/s avec une incertitude de mesure d'environ 1 m/s. En 1983, le mètre est redéfini dans le Système international d'unités (SI) comme la distance parcourue par la lumière dans le vide en 1/299 792 458 seconde[3] ; en conséquence, la valeur numérique de c en mètres par seconde est maintenant exacte, comme résultant de la définition du mètre.

Avant-propos

Le nom de cette constante est souvent source de confusions. Il est important de comprendre que la vitesse de la lumière n'est pas une constante physique en soi : elle coïncide avec la constante physique c à condition que les photons aient une masse identiquement nulle et que la propagation s'effectue dans le vide absolu.

Par ailleurs, il est nécessaire de définir soigneusement la vitesse dont on parle. En effet, lorsqu'une impulsion lumineuse est émise, la description de sa propagation peut faire intervenir différentes notions comme la vitesse de phase (vitesse de propagation d'une composante spectrale monochromatique), la vitesse de groupe (vitesse de propagation du maximum de l'impulsion lumineuse, parfois abusivement considérée comme la vitesse de propagation de l'information), la vitesse du front d'onde (vitesse du point initial de l'onde), etc. En réalité, elle n'a pas toujours un sens physique simple ; elle peut être supérieure à c ou même négative ; la vitesse de transport de l'énergie n'est pas directement mesurable et pose également des problèmes de sens physique simple.

D'après Sylvan C. Bloch[7], au moins huit vitesses différentes peuvent être utilisées pour caractériser la propagation de la lumière, à savoir : les vitesses (1) de phase, (2) de groupe, (3) d'énergie, (4) de signal, (5) la constante de vitesse relativiste, (6) la vitesse de rapport d'unités, (7) la centrovitesse et (8) la vitesse de corrélation[8]. Dans le vide, toutes ces vitesses sont égales à la constante c, mais dans un autre milieu, seule la vitesse du front d'onde conserve cette valeur.

En toute rigueur, la question de la constance de la vitesse de la lumière dans le vide, telle qu’observée par quanta d’énergie transportés par les photons, ne peut être totalement tranchée puisqu'il est théoriquement possible que les photons aient une masse non nulle : les mesures ne peuvent que plafonner cette masse hypothétique et non prouver qu'elle est rigoureusement nulle. Toutefois, même s'il était avéré que les photons ont une masse, cela ne remettrait pas en cause le principe de la constante c, mais donnerait plutôt une limite de précision de son observabilité dans les modèles de référence ; on conserverait avec c une limite absolue de vitesse que les photons observés ne pourraient pas eux-mêmes atteindre dans le vide[9].

Notations
Notations usuelles

La vitesse de la lumière dans le vide est couramment notée c, initiale de constante et de célérité. Sa vitesse dans tout autre milieu est couramment notée v, initiale de vitesse.

Bref historique

Le symbole V a été utilisé pour la vitesse de la lumière par James Clerk Maxwell en 1865. En 1856, Wilhelm Eduard Weber et Rudolf Kohlrausch utilisèrent c pour noter une autre constante égale à la vitesse de la lumière dans le vide multipliée par la racine carrée de deux. En 1894, Paul Drude redéfinit c comme le symbole pour la vitesse des ondes électromagnétiques. En 1905, Albert Einstein utilise V dans ses publications sur la relativité restreinte. Mais, en 1907, il opte pour c[10],[11].

Notations alternatives

La vitesse de la lumière dans un milieu transparent est parfois notée c. Sa vitesse dans le vide est alors notée c0, conformément à la recommandation du Bureau international des poids et mesures[12]. L'indice 0 indiquant que le milieu est le vide, comme dans les notations usuelles de la perméabilité magnétique du vide μ0, de la permittivité diélectrique du vide ε0 (on a ε0 μ0 c02 = 1) et de l'impédance caractéristique du vide Z0.

Dimension et unités

En analyse dimensionnelle, la vitesse de la lumière, dans le vide ou dans un milieu, a la dimension d'une vitesse.

Son équation aux dimensions est :

[c] = [V] = L T-1.

Dans le Système international d'unités, elle s'exprime en mètres par seconde (m s−1).

Valeur

Depuis 1983, la vitesse de la lumière dans le vide est exacte, par la définition du mètre. Celui-ci étant défini comme « la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 seconde », la vitesse de la lumière dans le vide est ainsi :

On peut se souvenir de la valeur de c en remplaçant chaque mot de la phrase suivante par le nombre de lettres qui le composent : « La constante lumineuse restera désormais là, dans votre cervelle », soit 2 9 9 7 9 2 4 5 8 m/s.

En unités géométriques et en unités de Planck, la vitesse de la lumière dans le vide est, par définition, réduite à un : c = 1.

Historique
Chronologie des valeurs estimées de c
AnnéeAuteur(s)TechniqueValeur
(en km/s)		Incertitude
(en km/s)		Référence(s)
< 1638GaliléeLanternes masquéesNon concluant-[13],[14],[15]
< 1667Accademia del CimentoLanternes masquéesNon concluant-[16],[15]
1675Ole Rømer et Christiaan HuygensObservation des lunes de Jupiter220 000 ?[17],[18]
1729James BradleyAberration de la lumière301 000 ?[19]
1849Hippolyte FizeauRoue dentée315 000 ?[19]
1862Léon FoucaultMiroir en rotation298 000500[19]
1907Bennett Rosa et Noah DorseyConstantes électromagnétiques299 71030[20],[21]
1926Albert A. MichelsonMiroir en rotation299 7964[22]
1950Louis Essen et Albert Gordon-SmithCavité résonnante299 792,53,0[23]
1958K. D. FroomeInterférométrie radio299 792,500,10[24]
1972Evenson et al.Interférométrie laser299 792,456 20,001 1[25]
1978Woods, Shotton et RowleyInterférométrie laser299 792,458 80,000 2[26]
1983Conférence générale des poids et mesures (définition du mètre)299 792,4580 (par construction)[27]

L'histoire des mesures de la vitesse de la lumière ne compte pas moins de douze méthodes pour déterminer la valeur de c[28]. Après les spéculations d’Empédocle, d’Alhazen ou de Roger Bacon, et les tentatives malheureuses de Galilée avec des aides démasquant des lanternes, la première estimation expérimentale est due à l’astronome danois Ole Christensen Rømer : en étudiant le cycle des éclipses de Io, satellite de Jupiter, il trouve que quarante révolutions observées lors d’une quadrature de Jupiter avec la Terre sont décalées dans le temps par rapport à quarante autres observées lorsque les deux planètes sont au plus proche. Il en déduit que quand Jupiter et la Terre sont en positions opposées par rapport au soleil, la lumière de Jupiter met 22 minutes de plus pour nous parvenir que lorsque les deux planètes sont au plus proche, ce retard correspondant au temps supplémentaire de parcours par la lumière du diamètre de l’orbite terrestre.

En , il prédit ainsi pour une émersion de Io, un retard de 10 minutes (observé le 9 novembre) par rapport à la table établie par Cassini. La lumière mettait ainsi 11 min pour parcourir le rayon de l’orbite terrestre, mais ce rayon était mal connu[29], les mesures étant dispersées entre 68 et 138 millions de kilomètres, valeurs toutes fausses. Ce travail est publié dans le Journal des sçavans, la plus ancienne revue littéraire et scientifique[30].

Rømer (qui trouva ensuite 7 min), Cassini, Newton et bien d’autres améliorèrent la précision du temps de parcours, mais il fallut attendre que Delambre analyse un millier d’éclipses, réparties sur 140 ans, pour trouver la valeur de 8 min 13 s (la valeur correcte est de 8 min 19 s).

L’étape suivante est due à James Bradley : en 1727, étudiant les variations de déclinaison de l’étoile Gamma du Dragon, il découvre le phénomène de l’aberration de la lumière, dû à la combinaison de la vitesse de la lumière avec celle de la Terre ; il en déduit que la vitesse de la lumière vaut 10 188 fois celle de la Terre. Mais la vitesse de la Terre était mal connue, puisqu’elle dépend du rayon de son orbite.

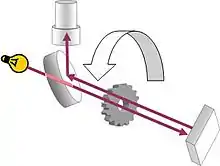
Schéma illustrant la mesure de la vitesse de la lumière par le système de roue dentée de Fizeau. La lumière passe à travers un miroir semi-réfléchissant puis à travers une échancrure de la roue dentée. Elle parcourt une certaine distance, se réfléchit sur un miroir et revient vers la roue qui, entre-temps, a tourné. La connaissance de la distance totale parcourue par la lumière et de la vitesse de rotation de la roue nécessaire à ce que la lumière, lors de son retour, soit bloquée par une dent de la roue, permet de déterminer la vitesse de la lumière.

La première mesure, indépendante d’une autre mesure, est faite par Hippolyte Fizeau, en 1849. En opérant entre Suresnes et Montmartre avec un dispositif à roue dentée, il trouve 315 000 km/s (donc majorée avec une erreur de seulement 5 %), un résultat déjà impressionnant pour l’époque, tout autant que l'instrumentation construite par Gustave Froment, avec une roue comprenant 720 dents usinées au centième de millimètre près.

Un nouveau progrès est fait par Léon Foucault avec un dispositif à miroir tournant, qui lui permet d’opérer sans sortir du laboratoire. En 1850, il montre que la lumière se déplace moins vite dans l’eau, en accord avec la théorie des ondulations. À l'Observatoire de Paris, en , il trouve[31] la valeur de 298 000 km/s.

Les mesures (et les méthodes) vont alors se multiplier. Sans les citer toutes :

  • en 1870, Alfred Cornu sur le principe de la roue dentée, invente une nouvelle méthode et trouve 298 500 km/s, en opérant entre l’École polytechnique et le mont Valérien. Il disqualifie peu après cette mesure, et en 1874, entre l’observatoire et la tour de Montlhéry, trouve 300 400 ± 300 km/s ;
  • en 1878, Albert Michelson (alors âgé de 25 ans) « bricole » un dispositif à miroir tournant et trouve 300 140 ± 480 km/s : c’est la première valeur donnant une mesure avec un intervalle de précision contenant la valeur actuelle, même si la valeur moyenne estimée est encore excessive ;
  • en 1882, Simon Newcomb, avec un miroir tournant, trouve 299 810 ± 50 km/s, pendant que Michelson trouve 299 853 ± 60 km/s. Ces résultats, compte tenu des intervalles de précision affichés, sont en contradiction avec ceux de Cornu, ce qui donne lieu à une controverse entre scientifiques français et américains. La méthode du miroir tournant n'est pas jugée assez fiable en France, les questions théoriques de physique soulevées par le mouvement du miroir n'ayant pas de réponse ;
  • Henri Perrotin en 1898 et en 1902 effectue deux séries de mesures, depuis l'Observatoire de Nice, sur des distances de 12 et 46 km avec l'instrument de Cornu, et trouve 299 880 ± 50 km/s, valeur plus proche de celles de Newcomb et Michelson que de celle de Cornu ;
  • en 1926, Michelson opère avec une base de 35 km, entre le mont Wilson et le mont San Antonio avec un dispositif s'inspirant du miroir tournant et de la roue dentée, pour s'affranchir d'éventuels effets dus à la vitesse de miroir. Il trouve 299 796 ± 4 km/s : cette fois l’intervalle de précision donné contient la valeur actuelle, même si c’est à sa limite inférieure.
Expérience de mesure de la lumière par Michelson en 1930.

Michelson imagina de faire l'expérience dans le vide. En 1929, il entreprit de faire construire près de Pasadena, un tube en acier d'un mile de long pour y faire une ultime expérience. Il mourut en 1931 sans en voir les résultats. Malgré des erreurs de mesures dues à des effets géologiques et des problèmes de construction du tube, les résultats finaux, 299 774 ± 11 km/s, étaient en accord avec les mesures électro-optiques de l'époque[32],[33].

Après la Seconde Guerre mondiale, le géodimètre, la cavité résonnante, le radar, le radio-interféromètre, la spectrométrie de bande, et surtout le laser, vont permettre un bond dans la précision :

  • en 1947, avec une cavité résonnante (un guide d'onde fermé), Louis Essen trouve 299 792 ± 3 km/s ;
  • en 1949, avec un radar, C.I. Aslakson trouve 299 792,4 ± 2,4 km/s. L’incertitude relative donnée passe sous la barre de ±1/125 000, mais l’erreur relative commise sur la valeur moyenne estimée n’est que de 1/5 200 000 ;
  • en 1958, Keith Davy Froome, avec un radio-interféromètre à ondes millimétriques, trouve 299 792,5 ± 0,1 km/s. C’est la meilleure mesure avant l’entrée en scène du laser ;
  • en 1972, Kenneth Evenson, avec un laser hélium-néon stabilisé, trouve 299 792,457 4 ± 0,001 1 km/s. La précision a fait un bond d’un facteur 100 ;
  • en 1975, à la suite des changements de plus en plus fréquents de la valeur moyenne estimée, et d’après les meilleurs résultats expérimentaux obtenus jusqu’alors (dont il reste à vérifier les conditions de reproductibilité), la 15e Conférence générale des poids et mesures recommande alors dans sa deuxième résolution la valeur de c égale à 299 792 458 m s-1[34] et invite ses membres et toute la communauté scientifique à réfléchir sur les différentes possibilités de corrélation avec les autres unités et constantes de référence, et notamment pour la redéfinition et l’étalonnage du mètre et/ou celle de la seconde ;
  • en 1978, Woods, Shotton et Rowley, avec le même type de laser qu’Evenson mais dans des conditions expérimentales plus strictes, trouvent 299 792,458 8 ± 0,000 2 km/s, avec la définition encore en vigueur du mètre de 1960[26]. La vitesse de la lumière est maintenant connue avec une meilleure précision que l’ancien mètre étalon ;
  • en 1983, la 17e Conférence générale des poids et mesures[35] en prend acte dans sa première résolution et change la définition du mètre :
    « Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 seconde. »

Par cette dernière définition, la communauté scientifique entérine la définition de la vitesse de la lumière dans le vide absolu (un vide théorique car il est seulement approché et simulé dans les modèles expérimentaux actuels) comme une constante universelle, sur laquelle se fondent ensuite toutes les mesures d’espace et de temps.

Elle comporte aussi l’avantage conséquent de ne plus se baser sur les raies spectrales d’éléments atomiques (auparavant une raie du krypton 86 depuis 1960, déjà difficile à purifier et isoler dans des états stables sur des échantillons suffisamment significatifs pour obtenir la précision souhaitée), ce qui élimine en même temps d’une part les sources d’imprécision ou d’incertitude relatives aux variétés isotopiques ou subatomiques (qui influent sur la largeur des raies spectrales encore actuellement mesurées) et d’autre part la nécessité de reproduire plus exactement des conditions de mesure basées sur un modèle expérimental (des conditions qui peuvent désormais évoluer indépendamment de cette définition et s’améliorer en précision à un coût moindre, en fonction des nouvelles découvertes), notamment à l'aide de mesure des fréquences (ou de façon équivalente) de longueurs d’onde de raies spectrales caractéristiques (qui restent à étudier pour mettre en pratique cette définition).

Cependant, elle présuppose encore l’existence d’un modèle expérimental pour l’établissement de la définition de la seconde, dont dépend alors celle du mètre puisque la vitesse de la lumière dans le vide dont dépend aussi cette définition est maintenant établie comme une constante universelle. C’est tout de même une amélioration du système puisqu’un des deux éléments de variabilité a été éliminé, et aussi parce que c’est dans le domaine de la mesure du temps (ou des fréquences) que les progrès les plus importants ont été obtenus en termes de précision.

Une définition similaire concernant l’unité de masse (ou de façon équivalente de celle d’énergie) pourrait aussi utiliser à terme la définition d’une constante universelle, quand le phénomène de gravitation sera mieux connu et maîtrisé pour mieux préciser la vitesse de la lumière dans un vide non idéal (puisque l’espace et le temps subissent l’influence de la gravitation, ce qui influe sur la vitesse effectivement mesurée de la lumière dans le vide réel toujours observé).

Vitesse de la lumière dans le vide

D’après les théories de la physique moderne, et notamment les équations de Maxwell, la lumière visible, et même le rayonnement électromagnétique en général, a une vitesse constante dans le vide ; c'est cette vitesse qu'on appelle vitesse de la lumière dans le vide.

C'est donc une constante physique fondamentale. Elle est notée c (du latin celeritas, « vitesse »). Elle n’est pas seulement constante en tout lieu (et à tout âge) de l’Univers (principes cosmologiques faible et fort, respectivement) ; elle est également constante d’un repère inertiel à un autre (Principe de relativité). En d’autres termes, quel que soit le repère inertiel de référence d’un observateur ou la vitesse de l’objet émettant la lumière, tout observateur obtiendra la même mesure.

La vitesse de la lumière dans le vide est notée c (valeur exacte recommandée depuis 1975, devenue exacte par définition depuis 1983) :

c = 299 792 458 mètres par seconde

Constance de c

Cette valeur est exacte par définition. En effet, depuis 1983, le mètre est défini à partir de la vitesse de la lumière dans le vide dans le Système international d'unités, comme étant la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1/299 792 458 de seconde[34]. Ce qui fait que le mètre est aujourd’hui défini par la seconde, via la vitesse fixée pour la lumière[34].

On pourrait objecter que la constance de la vitesse de la lumière quelle que soit la direction, pilier de la physique, est vraie par construction, par le choix des définitions des unités du système international. Cette objection est fausse parce que le choix d’une définition du mètre basée sur la seconde et la lumière est en fait une conséquence de la confiance absolue des physiciens en la constance de la vitesse de la lumière dans le vide ; cette confiance était exprimée alors que la définition du mètre de 1960 reposait sur un phénomène radiatif indépendant de celui définissant la seconde.

Cependant, il a été suggéré dans diverses théories que la vitesse de la lumière pourrait avoir varié au cours du temps[36],[37]. Aucune preuve concluante de tels changements n'a encore été mise en évidence, mais cela reste à ce jour un sujet de recherche[38],[39].

Interaction de la lumière avec la matière

La différence de vitesse de propagation de la lumière dans des milieux différents est à l’origine du phénomène de réfraction. La vitesse dans un milieu donné par rapport à la vitesse dans le vide est égale à l'inverse de l’indice de réfraction (ce dernier dépendant par ailleurs de la longueur d’onde) :

où :
  • c est la vitesse de la lumière dans le vide ;
  • v est la vitesse de la lumière dans le milieu d'indice n. L'indice n du vide est égal par définition à 1.

Cependant, la vitesse de la lumière, sans autre précision, s’entend généralement pour la vitesse de la lumière dans le « vide ».

Notons que si aucun objet dans quelque milieu que ce soit ne peut dépasser la vitesse de la lumière dans le vide, dépasser la vitesse de la lumière dans un même milieu est possible : par exemple dans l’eau, les neutrinos vont considérablement plus vite que la lumière (qui s’y trouve elle-même considérablement ralentie). Dans le cas de particules chargées, comme les électrons ou positons issus de la désintégration β cela provoque l'équivalent du bang supersonique pour la lumière, c'est l’effet Tcherenkov qui « teinte » en bleu le fond des piscines contenant du matériel radioactif.

Pour finir, dans un milieu dit biréfringent, la vitesse de la lumière dépend aussi de son plan de polarisation. Ce phénomène très particulier est utilisé dans de très nombreux domaines comme en microscopie ou pour les lunettes de soleil[40].

Limite de la vitesse de la lumière
Composition de vitesses relativistes. Les vitesses sont exprimées en prenant pour unité la vitesse de la lumière.

La vitesse de la lumière dans le vide n’est pas une vitesse limite au sens conventionnel. Nous avons l’habitude d’additionner des vitesses, par exemple nous estimerons normal que deux voitures roulant à 60 kilomètres à l’heure en sens opposés se voient l’une et l’autre comme se rapprochant à une vitesse de 60 km/h + 60 km/h = 120 km/h. Et cette formule approchée est parfaitement légitime pour des vitesses de cet ordre (60 km/h ≈ 16,67 m/s).

Mais, lorsque l’une des vitesses est proche de celle de la lumière dans le vide, un tel calcul classique s’écarte trop des résultats observés ; en effet, dès la fin du XIXe siècle, diverses expériences (notamment, celle de Michelson) et observations laissaient apparaître une vitesse de la lumière dans le vide identique dans tous les repères inertiels.

Minkowski, Lorentz, Poincaré et Einstein introduisirent cette question dans la théorie galiléenne, et s’aperçurent de la nécessité de remplacer un principe implicite et inexact par un autre compatible avec les observations :

  • il fallait renoncer à l’additivité des vitesses (admise par Galilée sans démonstration) ;
  • introduire un nouveau concept, la constance de c (constatée par l’expérience).
Diagramme des compositions de vitesses. Le côté asymptotique de la vitesse c (ici, 1) apparaît nettement.

Après mise en forme calculatoire, il se dégagea que la nouvelle formule de composition comportait un terme correctif en 1/(1 + v w/c2), de l’ordre de 2,7×10-10 seulement à la vitesse du son.

L’effet devient plus grand lorsque les vitesses dépassent c/10, et de plus en plus visible à mesure que v/c se rapproche de 1 : deux vaisseaux spatiaux voyageant l’un vers l’autre à la vitesse de 0,8 c (par rapport à un troisième observateur), ne percevront pas une vitesse d’approche (ou vitesse relative) égale à 1,6 c, mais seulement 0,98 c (voir tableau ci-contre).

Ce résultat est donné par la transformation de Lorentz :

où :
  • v et w sont les vitesses des vaisseaux spatiaux ;
  • u est la vitesse perçue d'un vaisseau depuis l’autre.

Ainsi, quelle que soit la vitesse à laquelle se déplace un objet par rapport à un autre, chacun mesurera la vitesse de l’impulsion lumineuse reçue comme ayant la même valeur : la vitesse de la lumière ; en revanche, la fréquence observée d’un rayonnement électromagnétique transmis entre deux objets en déplacement relatif (ainsi que les quantums d’énergie associée entre le rayonnement émis et le rayonnement perçu par l’objet cible) sera modifiée par effet Doppler-Fizeau.

Albert Einstein unifia les travaux de ses trois collègues en une théorie de la relativité homogène, appliquant ces étranges conséquences à la mécanique classique. Les confirmations expérimentales de la théorie de la relativité furent au rendez-vous, à la précision des mesures de l’époque près.

Dans le cadre de la théorie de la relativité, les particules sont classées en trois groupes :

  • les bradyons, particules de masse au repos réelle, se déplacent à des vitesses inférieures à c ;
  • les luxons, particules de masse au repos nulle, se déplacent uniquement à la vitesse c dans le vide ;
  • les tachyons, particules hypothétiques dont la masse au repos est un nombre imaginaire, se déplacent, par définition, uniquement à des vitesses supérieures à c, s'ils existent ; la plupart des physiciens considèrent que ces particules n’existent pas (pour des raisons de causalité selon les principes actuels).

Les masses au repos combinées avec le facteur multiplicatif donnent une énergie réelle pour chacun des groupes définis précédemment.

Cas de dépassements apparents

Ce qu'interdit la relativité restreinte, c'est de violer la causalité : c'est donc l'information au sens causal du terme qui ne peut pas aller plus vite que c. L'un des problèmes est d'arriver à définir cette notion d'information. En effet, il est par exemple possible qu'une impulsion lumineuse ait une vitesse de groupe supérieure à c sans que cela viole la causalité car le front d'onde se propage lui à la vitesse c.

Il a en fait été montré que l'information se propage toujours à la vitesse c[alpha 3] : les vitesses de la lumière infra ou supraluminiques peuvent transporter un signal, mais pas de l'information au sens causal. De manière générale, il est donc important de faire attention à la définition de la vitesse considérée. En plus de la vitesse de l'information (le concept d'information étant parfois difficile à définir), on peut ainsi considérer différentes vitesses qui peuvent prendre des valeurs inférieures ou supérieures à c, voire des valeurs négatives[41],[42] :

Le paradoxe EPR a également montré que la physique quantique donne des exemples pour lesquels les particules se comportent comme si elles pouvaient se coordonner, alors que les écarts dans l'espace et le temps réclameraient pour cela de dépasser c. Cependant, ce phénomène ne peut pas être utilisé pour transmettre de l'information.

En , la collaboration de physiciens travaillant sur l'expérience OPERA annonce que le temps de vol mesuré des neutrinos produits au CERN est inférieur de 60,7 ns à celui attendu pour des particules se déplaçant à la vitesse de la lumière[43],[44]. Le , les scientifiques de l'expérience OPERA annoncent que l'anomalie était en fait liée à une erreur de mesure due au branchement défectueux d’un câble de synchronisation optique des horloges atomiques, et que la vitesse mesurée des neutrinos était compatible avec celle de la lumière[45].

Notes et références

Notes
  1. Cette valeur est prise comme définition du mètre (en fonction de la seconde) depuis 1983.
  2. Depuis quelques années pour les étoiles les plus proches jusqu'à quelques milliards d'années pour les plus lointaines.
  3. (en) Stenner et al., Nature, 425, p. 695 (2003) montrent que dans le cas d'une impulsion lumineuse supraluminique, l'information se propage à c, et Stenner et al., Phys. Rev. Lett., 94, p053902 (2005) montrent que c'est également vrai dans le cas de vitesses de groupe petites.

Références
  1. « Combien de temps faut-il à la lumière réfléchie par la Lune pour parvenir jusqu'à nous ? - L'Étoile des enfants », sur etoile-des-enfants.ch (consulté le )
  2. Marc Séguin et Benoît Villeuneuve, Astronomie et astrophysique : Cinq grandes idées pour explorer et comprendre l'Univers, vol. 2, ERPI, , 618 p. (ISBN 978-2-7613-1184-7), p. 121
  3. « Résolution 2 de la 15e CGPM (1975) - Valeur recommandée pour la vitesse de la lumière », sur bipm.org, Bureau international des poids et mesures, (consulté le )
  4. (en) Jean-Philippe Uzan et Bénédicte Leclercq, The Natural Laws of the Universe : Understanding Fundamental Constants, New York, NY, Springer Science & Business Media, (ISBN 978-0-387-74081-2, lire en ligne)
  5. « How is the speed of light measured? », (consulté le )
  6. (en) John Stachel, Einstein from 'B' to 'Z', Springer Science & Business Media, , 556 p. (ISBN 978-0-8176-4143-6, lire en ligne)
  7. (en) Sylvan C. Bloch, « Eight velocities of light », American Journal of Physics, vol. 45, no 6,‎ , p. 538-549 (DOI 10.1119/1.10953, lire en ligne, consulté le )
  8. (en) Richard L. Smith, « The velocities of light », American Journal of Physics, vol. 38, no 8,‎ , p. 978-984 (DOI 10.1119/1.1976551, Bibcode 1970AmJPh..38..978S)
  9. Cours d'Optique de l'École normale supérieure
  10. (en) Philip Gibbs, « Why is c the symbol for the speed of light? », sur Department of Mathematics. University of California. Riverside, (consulté le )
  11. (en) Kenneth S. Mendelson, « The story of c », American Journal of Physics, vol. 74, no 11,‎ , p. 995-997 (DOI 10.1119/1.2238887, Bibcode 2006AmJPh..74..995M)
  12. Bureau international des poids et mesures, Le Système international d'unités (SI), Sèvres, BIPM, , 9e éd., 216 p. (ISBN 978-92-822-2272-0, lire en ligne [PDF]), chap. 2.3.1 (« Unités de base »), p. 19
  13. G. Galilei (Crew, H. ; de Salvio A. (trans.)), Dialogues Concerning Two New Sciences, Dover Publications, (1re éd. 1638) (ISBN 0-486-60099-8, lire en ligne), p. 43
  14. (en) C.B. Boyer, « Early Estimates of the Velocity of Light », Isis, vol. 33, no 1,‎ , p. 24 (DOI 10.1086/358523)
  15. Renato Foschi et Matteo Leone, « Galileo, measurement of the velocity of light, and the reaction times », Perception, vol. 38,‎ , p. 1251–9 (DOI 10.1068/p6263, lire en ligne, consulté le )
  16. Magalotti, « Saggi di Naturali Esperienze fatte nell' Accademia del Cimento », Saggi di Naturali, Florence, Istituto e Museo di Storia delle Scienze,‎ (lire en ligne, consulté le )
  17. « Touchant le mouvement de la lumière trouvé par M. Rŏmer de l'Académie Royale des Sciences », Journal des sçavans,‎ , p. 233–36 (lire en ligne)
  18. C. Huygens, Traitée de la Lumière, Pieter van der Aa, , 8–9 p. (lire en ligne)
  19. (en) P. Gibbs, « How is the speed of light measured? », Usenet Physics FAQ, University of California, Riverside, (consulté le )
  20. (en) L. Essen et A.C. Gordon-Smith, « The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator », Proceedings of the Royal Society of London A, vol. 194, no 1038,‎ , p. 348–361 (DOI 10.1098/rspa.1948.0085, JSTOR 98293, Bibcode 1948RSPSA.194..348E)
  21. (en) E.B. Rosa et N.E. Dorsey, « The Ratio of the Electromagnetic and Electrostatic Units », Bulletin of the Bureau of Standards, vol. 3, no 6,‎ , p. 433 (DOI 10.1103/PhysRevSeriesI.22.367, Bibcode 1906PhRvI..22..367R)
  22. A.A. Michelson, « Measurement of the Velocity of Light Between Mount Wilson and Mount San Antonio », The Astrophysical Journal, vol. 65,‎ , p. 1 (DOI 10.1086/143021, Bibcode 1927ApJ....65....1M)
  23. (en) L. Essen, « The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator », Proceedings of the Royal Society of London A, vol. 204, no 1077,‎ , p. 260–277 (DOI 10.1098/rspa.1950.0172, JSTOR 98433, Bibcode 1950RSPSA.204..260E)
  24. (en) K.D. Froome, « A New Determination of the Free-Space Velocity of Electromagnetic Waves », The Royal Society, vol. 247, no 1248,‎ , p. 109–122 (DOI 10.1098/rspa.1958.0172, JSTOR 100591, Bibcode 1958RSPSA.247..109F)
  25. (en) K.M. Evenson et al., « Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser », Physical Review Letters, vol. 29, no 19,‎ , p. 1346–49 (DOI 10.1103/PhysRevLett.29.1346, Bibcode 1972PhRvL..29.1346E)
  26. Résolution 6 de la 11e CGPM (1960) - Définition du mètre.
  27. « Résolution 1 de la 17e CGPM (1983) : Définition du mètre », BIPM, (consulté le )
  28. Dominique Raynaud, « Les déterminations de la vitesse de la lumière (1676-1983) : Étude de sociologie internaliste des sciences », L'Année sociologique, vol. 63, no 2,‎ , p. 359-398 (DOI 10.3917/anso.132.0359)
  29. James Lequeux, Römer démontre que la vitesse de la lumière n'est pas infinie, Encyclopædia Universalis (lire en ligne).
  30. « Demonstration touchant le mouvement de la lumiere »,
  31. Observatoire de Paris — « c » à Paris, vitesse de la lumière : histoire et expérience
  32. « Michelson's Last Experiment », Science, vol. 73, no 1899,‎ , p. 10–14 (PMID 17843974, DOI 10.1126/science.73.1899.10)
  33. A. A. Michelson, F. G. Pease et F. Pearson, « Measurement of the velocity of light in a partial vacuum », Contributions from the Mount Wilson Observatory, vol. 522, no 2091,‎ , p. 100–1 (PMID 17816642, DOI 10.1126/science.81.2091.100-a, lire en ligne)
  34. « Brochure sur le Système international d'unités (SI) », sur Bipm.org, Bureau international des poids et mesures, (consulté le )
  35. Résolution 1 de la 17e CGPM (1983).
  36. G.F.R. Ellis et J.-P. Uzan, « ‘c’ is the speed of light, isn’t it? », American Journal of Physics, vol. 73, no 3,‎ , p. 240–7 (DOI 10.1119/1.1819929, Bibcode 2005AmJPh..73..240E, arXiv gr-qc/0305099) :
    « The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today. »
  37. D.F. Mota, « Variations of the Fine Structure Constant in Space and Time » (PhD), Thèse,‎ (Bibcode 2004astro.ph..1631M, arXiv astro-ph/0401631, lire en ligne)
  38. J.-P. Uzan, « The fundamental constants and their variation: observational status and theoretical motivations », Reviews of Modern Physics, vol. 75, no 2,‎ , p. 403 (DOI 10.1103/RevModPhys.75.403, Bibcode 2003RvMP...75..403U, arXiv hep-ph/0205340)
  39. G. Amelino-Camelia, « Quantum Gravity Phenomenology », Living Reviews in Relativity, vol. 16,‎ (DOI 10.12942/lrr-2013-5, Bibcode 2013LRR....16....5A, arXiv 0806.0339)
  40. « STROCK - Verre - Tensions », sur strock.pi.r2.3.14159.free.fr (consulté le )
  41. (en) D. Gauthier et R. Boyd, « Fast Light, Slow Light and Optical Precursors: What Does It All Mean? », Photonics Spectra,‎ (lire en ligne [PDF]).
  42. (en) Peter W. Milonni, Fast light, slow light, and left-handed light, Bristol Philadelphia, Institute of Physics, , 247 p. (ISBN 978-0-7503-0926-4, OCLC 57283882).
  43. L’expérience OPERA annonce une anomalie dans le temps de vol des neutrinos allant du CERN au Gran Sasso (communiqué de presse), CERN, 23 septembre 2011.
  44. (en) T. Adam et al., « Measurement of the neutrino velocity with the OPERA detector in the CNGS beam », sur arXiv, (consulté le )
  45. Sylvestre Huet, « Neutrinos plus rapides que la lumière ? Non et fin de l'histoire », sur Libération, (consulté le ).

Voir aussi

Bibliographie

Articles connexes

Liens externes
  • Portail de la physique
  • Portail de l’optique
  • Portail de l’astronomie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.