< Matrice
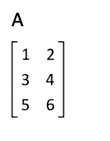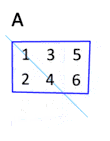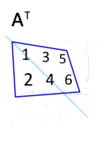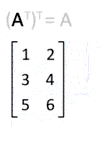

La transposée AT d'une matrice A s'obtient par symétrie axiale par rapport à la diagonale principale de la matrice. La transposée de la transposée (AT)T est la matrice A d'origine.
Définition
La matrice transposée (on dit aussi la transposée) d'une matrice est la matrice notée (aussi parfois notée ou ), obtenue en échangeant les lignes et les colonnes de .
Si B = tA alors .
Propriétés
On suppose ici que K est un corps commutatif (par exemple ou ).
- L'application « transposition » est linéaire :.
- La transposée de est . L'application « transposition » est par conséquent (non seulement linéaire, mais aussi) bijective. C'est donc un isomorphisme d'espaces vectoriels. Sur l'espace de matrices carrées , c'est une involution donc une symétrie.
- La transposée du produit de deux matrices est égale au produit des transposées de ces deux matrices, mais dans l’ordre inverse :.
Démonstration
- Si une matrice carrée est inversible, alors sa transposée l'est aussi, et la transposée de l'inverse de est égale à l'inverse de sa transposée :.
- Une matrice carrée et sa transposée ont même diagonale principale (et par conséquent même trace).
- Plus généralement, deux matrices carrées transposées l'une de l'autre ont même polynôme caractéristique donc mêmes valeurs propres, comptées avec leurs multiplicités (en particulier, non seulement même trace mais aussi même déterminant), et même polynôme minimal.
| Pour plus de détails sur la transposée, voir la leçon Trace et transposée de matrice (de niveau 15). |
Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.