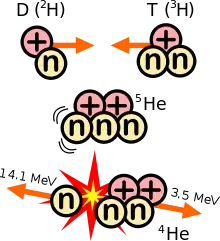
Fusion nucléaire
La fusion nucléaire (ou thermonucléaire) est le processus dans lequel deux noyaux atomiques s’assemblent pour former un noyau plus lourd. Cette réaction est à l’œuvre de manière naturelle dans le Soleil et la plupart des étoiles de l'Univers, dans lesquelles sont créés tous les éléments chimiques autres que l'hydrogène et la majeure partie de l'hélium. Elle est, avec la fission nucléaire, l’un des deux principaux types de réactions nucléaires appliquées.
Ne doit pas être confondu avec Fusion du cœur d'un réacteur nucléaire ou Fusion (changement d'état).
Cet article concerne la recherche sur la fusion nucléaire contrôlée. Pour la fusion nucléaire explosive, voir Bombe H. Pour la fusion nucléaire naturelle, voir Nucléosynthèse stellaire.
La fusion nucléaire dégage une quantité d’énergie colossale par unité de masse, provenant de l’attraction entre les nucléons due à l’interaction forte (voir énergie de liaison nucléaire). La masse du ou des produits d'une réaction de fusion étant inférieure à la somme des masses des noyaux fusionnés, la différence est transformée en énergie cinétique (puis en chaleur) selon la formule d'Einstein E = mc2.
La fusion nucléaire est utilisée dans les bombes H et, de façon plus anecdotique, dans les générateurs de neutrons. Elle pourrait être utilisée pour la production d'électricité, pour laquelle elle présente deux intérêts majeurs :
- la disponibilité de son « combustible » :
- le deutérium, présent à l'état naturel en quantités importantes dans les océans,
- le tritium (pour la réaction de fusion « deutérium + tritium »), qui peut être produit par bombardement neutronique du lithium 6. Les réserves mondiales en minerai de lithium suffiraient théoriquement à garantir plus d'un million d'années de fonctionnement ;
- son caractère essentiellement « propre » : les produits de la fusion eux-mêmes (principalement de l’hélium 4) ne sont pas radioactifs. Les déchets potentiels se limitent, lorsque la réaction utilisée émet des neutrons rapides, aux matériaux environnants, qui peuvent capturer ces neutrons et devenir à leur tour des isotopes radioactifs.
En dépit de travaux de recherche réalisés dans le monde entier depuis les années 1950, aucune application industrielle de la fusion à la production d’énergie n’a encore abouti. Les ingénieurs se heurtent à la difficulté de créer et de maintenir une température de plusieurs millions de degrés dans un espace confiné.
La fusion nucléaire n'a rien à voir avec la fusion du cœur d'un réacteur nucléaire, qui est un accident nucléaire particulièrement redoutable[alpha 1].
Histoire
La découverte des réactions de fusion date du début du XXe siècle. Après quelques expériences, l'astrophysicien Arthur Eddington suggère en 1920 que l'énergie des étoiles est due à la fusion de noyaux d'hydrogène en hélium. En 1934, Ernest Rutherford réalise la première réaction de fusion en laboratoire (entre atomes de deutérium)[1].
En 1938, les travaux de Hans Bethe et Carl Friedrich von Weizsäcker aboutissent à la formule de Weizsäcker, qui donne une valeur approximative de l'énergie de liaison entre les nucléons dans le noyau atomique. À partir de cette formule, ils imaginent les réactions qui se produisent à l'intérieur des étoiles. En 1950, George Gamow étudie celles qui ont pu avoir lieu juste après le Big Bang[2]. Il analyse notamment l'effet tunnel quantique comme permettant d'expliquer la fréquence des réactions de fusions de nucléons se produisant dans les étoiles[3].
Dans les années 1940, ces études montrent que les éléments produits dans une réaction de fusion sont beaucoup moins nombreux et ont une période radioactive nettement plus courte que les déchets générés par la fission nucléaire, sans compter que les ressources naturelles permettant la fusion sont disponibles en quantités gigantesques[4]. La fusion créée dans les étoiles grâce à la très forte gravité est alors envisagée sur Terre à l'aide de champs magnétiques, procédé appelé fusion magnétique[5].
En 1946, les physiciens britanniques George Paget Thomson et Moses Blackman déposent le premier brevet de réacteur à fusion nucléaire. Ils proposent une chambre à vide de forme torique pour confiner un plasma[6]. Inventé au début des années 1950 par les physiciens soviétiques Igor Tamm et Andreï Sakharov sur une idée originale du physicien Oleg Lavrentiev, l’acronyme tokamak vient du russe et se traduit par « chambre toroïdale avec bobines magnétiques ».
Du fait de la guerre froide, plusieurs pays lancent leurs recherches isolément et dans le plus grand secret (États-Unis, URSS, Angleterre, France, Allemagne et Japon)[4].
En janvier 1958, les Anglais annoncent avoir obtenu des neutrons issus de réactions de fusion : les vérifications montrent que ces neutrons viennent en fait de l'instabilité du plasma. Cet échec provoque la mutualisation des recherches au niveau mondial, annoncée en septembre de la même année à Genève, pendant le congrès du programme Atoms for Peace (« Atomes pour la paix »)[6]. En 1968, deux tokamaks russes, T3 et TM3, permettent à un plasma de dépasser la température de dix millions de degrés Celsius pendant 20 millisecondes. Cette voie de recherche est dès lors considérée comme la plus prometteuse[7].
La perspective d'une source d'énergie quasiment inépuisable attise les convoitises alors que le premier choc pétrolier et la prospective démographique démontrent la précarité des ressources eu égard aux besoins énergétiques croissants[8]. Les années 1970-1980 sont le théâtre d'une course effrénée à la recherche expérimentale[9] et des sommes considérables sont dépensées sans que l'objectif d'obtenir un bilan énergétique positif soit atteint[10] ; les États-Unis dépensent jusqu'à 500 millions de dollars par an dans ce cadre. La plupart des crédits sont destinés au développement de tokamaks de plus en plus puissants. D'autres domaines de recherche sont explorés. Le confinement inertiel par laser de plasma est expérimenté avec des lasers de puissance, le confinement radial par solénoïde est envisagé (field-reversed configuration (en), FRC), des expérimentations de faible puissance de confinement par auto-organisation du plasma en raison de ses propriétés magnétohydrodynamiques dans un volume sphérique ou sphéromak [11]sont réalisées.
Dans les années 1990, l'avenir du tokamak traditionnel s'assombrit en raison de la prise de conscience de ses limites portant sur la performance. Celle-ci est exprimée par le rapport β (bêta) du plasma, défini comme le rapport de la pression du plasma à la pression magnétique. À l’époque, le confinement magnétique est considéré comme la seule voie permettant d’atteindre les températures nécessaires à l’obtention de réactions de fusions autorisant un bilan énergétique positif. Il est unanimement convenu que ce facteur ne peut pas dépasser 5 %[12], ce qui implique de dépenser beaucoup d’énergie dans la réalisation d’aimants de plus en plus puissants. Les crédits de recherche se tarissent. Le projet ITER voit son budget de construction décupler et les retards se multiplier[13]. En 1997, le premier tokamak sphérique « moderne », le START (en)[14], établit un nouveau record, portant le β toroïdal à 38 %. En Allemagne une autre voie de recherche, variation autour du tokamak, est réalisée avec la construction d'un stellarator[15], le Wendelstein 7-X[16],[17], projet datant de 1994 mais finalement livré en 2015.
L'espoir renaît, le projet ITER décolle enfin et la construction est lancée en 2011. Les premiers plasmas sont prévus pour 2025[18]. L'on pense déjà à l'après-ITER, que préfigurent de nouveaux designs de dispositif plus compacts et plus puissants. Plusieurs designs de tokamak sphérique de démonstration (Spherical Tokamak for Energy Production (en)) sont proposés et les entreprises privées se lancent dans la course[19],[20],[21].
Le , la Chine met en marche le plus performant de ses tokamaks, HL-2M. Situé dans la province du Sichuan, il s'inscrit dans le programme ITER[22].
Mécanisme de la fusion
Répulsion électrique
Une réaction de fusion nucléaire[23] nécessite que deux noyaux atomiques s’interpénètrent. Il faut pour cela que les noyaux surmontent l'intense répulsion due à leurs charges électriques toutes deux positives (phénomène dit de « barrière coulombienne »). Si l’on appliquait uniquement les lois de la mécanique classique, la probabilité d’obtenir la fusion des noyaux serait très faible, en raison de l’énergie cinétique (correspondant à l’agitation thermique) extrêmement élevée nécessaire au franchissement de la barrière. Cependant, la mécanique quantique prévoit, ce qui se vérifie en pratique, que la barrière coulombienne peut également être franchie par effet tunnel, à des énergies plus faibles.
Température très élevée
Les énergies nécessaires à la fusion restent très élevées, correspondant à des températures de plusieurs dizaines ou même centaines de millions de degrés Celsius selon la nature des noyaux (voir plus bas : plasmas de fusion). Au sein du Soleil, par exemple, la fusion de l’hydrogène, qui aboutit, par étapes, à produire de l’hélium, s’effectue à des températures de l’ordre de quinze millions de kelvins, mais suivant des schémas de réaction différents de ceux étudiés pour la production d’énergie de fusion sur Terre. Dans certaines étoiles plus massives, des températures plus élevées permettent la fusion de noyaux plus lourds.
Émission de particules
Lorsque deux noyaux fusionnent, le noyau résultant se retrouve dans un état instable et doit revenir à un état stable d’énergie plus faible, en éjectant une ou plusieurs particules (photon, neutron, proton, noyau d’hélium, selon le type de réaction). L’énergie excédentaire se répartit entre le noyau et les particules émises, sous forme d’énergie cinétique.
Bilan d'énergie
Dans une perspective d'exploitation commerciale, pour que la fusion puisse être énergétiquement rentable, il est nécessaire que l’énergie produite soit supérieure à l’énergie consommée pour l’entretien des réactions et par pertes thermiques vers le milieu extérieur. Dans les réacteurs à fusion, il faut ainsi éviter tout contact entre le milieu de réaction et les matériaux de l’environnement, ce que l’on réalise par un confinement immatériel (magnétique ou inertiel).
Des noyaux légers et stables
Les réactions de fusion qui dégagent le plus d’énergie sont celles qui impliquent les noyaux les plus légers. Ainsi, les noyaux de deutérium 2
1D (un proton p+ et un neutron n) et de tritium 3
1T (un proton et deux neutrons) sont impliqués dans les réactions suivantes (où 3
2He est l'hélium 3 et 4
2He l'hélium 4) :
Dispositifs expérimentaux
Si la fission nucléaire est contrôlée depuis longtemps pour la production d'électricité, ce n'est pas le cas de la fusion.
Cette réaction est difficile à réaliser car il faut rapprocher deux noyaux qui ont tendance naturellement à se repousser. Maîtriser sur Terre la fusion de noyaux légers, tels que le deutérium, donnerait accès à des ressources énergétiques dans des quantités jamais rencontrées jusqu'alors par l'espèce humaine et produirait beaucoup moins de déchets nucléaires que la fission. Cet enjeu considérable a mené les communautés scientifiques nationales et internationales à lancer plusieurs projets d'envergure.
Il existe différents procédés concevables permettant d’arriver à confiner le milieu de réaction pour produire des réactions de fusion nucléaire, notamment la fusion par confinement magnétique et la fusion par confinement inertiel.
Fusion par confinement magnétique
Dans ces configurations, les particules composant le plasma suivent une trajectoire dépendant de leurs propriétés magnétohydrodynamiques et des lignes d'un champ magnétique généré par le plasma lui-même ou par des aimants. Les particules reviennent ainsi à leur position initiale (configuration fermée) ou suivent un chemin les amenant à sortir du dispositif (configuration ouverte).

Le tokamak torique
Le tokamak est le candidat favori au développement d'une centrale de production d'électricité par fusion contrôlée[24]. Il fonctionne selon le principe d'un échange de chaleur et d'un fluide caloporteur.
Dans un premier temps, il s'agit de démontrer, avec le réacteur expérimental ITER, que l'énergie produite par les réactions de fusion est supérieure à l'énergie consommée pour maintenir le plasma en conditions.
Le tokamak sphérique
Les tokamaks sphériques sont des dispositifs de confinement magnétique de plasma permettant de réaliser des réactions de fusion de nucléons de manière beaucoup plus efficace que les tokamaks traditionnels toriques.
Les expérimentations actuelles confirment le potentiel des tokamaks sphériques. Tous les marqueurs d’efficience sont d’un ordre dix fois supérieur au tokamak traditionnel[25],[26],[27].
Le stellarator
Dans un stellarator, le confinement du plasma est entièrement réalisé par un champ magnétique hélicoïdal généré par l'arrangement complexe de bobines autour du tore[28]. L'objectif est de maîtriser la trajectoire de chaque particule, ce qui est impossible dans un tokamak traditionnel torique en raison de la géométrie du tore : pour réaliser un tour, les particules coté intérieur au tore parcourent une distance plus petite que celles du coté extérieur au tore. Exemple de stellarator : le Wendelstein 7-X.
Le sphéromak
De forme sphérique, le sphéromak suit un principe d’auto-organisation du plasma grâce à ses propriétés magnétohydrodynamiques. Le flux de plasma, par sa forme, génère un champ magnétique qui à son tour le renforce et le stabilise. Certains dispositifs sont des hybrides de sphéromak et de tokamak sphérique (ex. : Proto-Sphera[29],[30]).
La startup canadienne General Fusion, qui développe à Vancouver un prototype de sphéromak avec le soutien d'investisseurs, dont le gouvernement britannique et Jeff Bezos[31], annonce le qu'elle construira de 2022 à 2025 son premier démonstrateur sur le campus de l'Autorité britannique de l'énergie atomique à Culham, à l'ouest de Londres. La puissance de la centrale sera de 115 MW[32].
Configurations ouvertes
Les dispositifs à piège à miroirs magnétiques et field-reversed configuration (en) (FRC)[33],[34] pourraient être utilisés pour la propulsion spatiale de type électrique.
Chauffage dans la fusion par confinement magnétique
Divers moyens sont à la disposition des physiciens de la fusion pour chauffer le plasma de deutérium et de tritium.
Un premier moyen est constitué par un système permettant d’engendrer un intense courant électrique au sein du plasma. Dans la mesure où des électrodes pollueraient le plasma, les chercheurs induisent ce courant grâce à un champ magnétique variable, soit croissant, soit décroissant. Ainsi, le courant induit possède des limites.
Il est aussi possible de chauffer le plasma au moyen d’un faisceau d’atomes neutres. Ces derniers sont, dans un dispositif distinct, ionisés pour pouvoir être accélérés par un champ électrique. Ils sont ensuite neutralisés par rattachement de leurs électrons, puis injectés dans le plasma. Ces atomes doivent nécessairement être neutres, puisque des ions seraient déviées par le champ de confinement et ne seraient pas en mesure d’accéder au centre du plasma. Une fois au centre de ce dernier, les atomes neutres s’ionisent à nouveau et, du fait de leur excédent énergie cinétique par rapport à celle du tritium et du deutérium, cèdent une partie de leur énergie au milieu par des collisions. Ces atomes neutres sont eux-mêmes de tritium et de deutérium. Ils assurent donc ainsi également l’approvisionnement en combustible.
Fusion par confinement inertiel
Dans cette voie, l'énergie est apportée par un faisceau de lumière laser ou bien par un faisceau de particules chargées (électrons ou ions) à une bille de combustible de quelques millimètres de diamètre. L'ionisation et le chauffage rapide de la paroi externe de la cible conduit à une expansion du plasma, à une vitesse égale à environ c/1 000, (c désignant la célérité de la lumière dans le vide, soit environ 3 × 108 m/s). Il s'ensuit l'apparition d'une onde de choc centripète, qui va concentrer le combustible deutérium-tritium au centre de la cible, dans un diamètre environ dix fois plus faible que le diamètre initial. On parle d'effet fusée pour qualifier cette convergence de la masse de la cible opposée à l'expansion du plasma périphérique (principe des actions réciproques de la troisième loi de Newton). Cette compression conduit à la fois à densifier le milieu combustible (environ 1 000 fois, soit : 10×10×10), pour donner une densité nulle part accessible sur Terre, à savoir 1026, et une température d'environ dix millions de degrés. Ces conditions conduisent à un nombre très important de réactions de fusion, pendant environ 10 picosecondes.
- Les machines à confinement inertiel par laser, où une microbille de deutérium-tritium enfermée dans une coquille de plastique est éclairée par de puissants lasers dont la puissance dépasse un pétawatt (exemple : Laser Mégajoule, National Ignition Facility) ; un gain de 10 entre l'énergie de fusion et l'énergie apportée par laser (environ 1,8 MJ) est attendu dans les expériences qui commenceront dans les années 2010. En 2014, les chercheurs du NIF sont parvenus à dégager le premier rendement positif (de l'ordre de 1,7 soit de 170 %) pour ce type de dispositif[35],[36].
- Les machines à striction axiale (ou Z-pinch), où une pastille d’isotopes est comprimée par des impulsions de rayons X (exemple : Z machine (plus de deux milliards de degrés atteints) des Laboratoires Sandia). Les conditions de fusion ont été obtenues en mars 2006 dans une Z machine à confinement axial[37]. Les travaux ont commencé sur la conception d’un réacteur expérimental à impulsion utilisant ce principe.
État d'avancement des projets
État d'avancement des principaux projets de fusion nucléaire contrôlée () :
| Projet | Catégorie | Date de mise en service | Résultats | Difficultés rencontrées | Commentaires |
|---|---|---|---|---|---|
| Commonwealth Fusion Systems | Tokamak | 2025 | (projet en construction) | ||
| ITER | Tokamak | 2025[38] | N/A
(projet en construction) |
Délai de construction,
budget dépassé[13] |
Projet international (35 pays) qui s'inscrit dans une démarche à long terme visant à l'industrialisation de la fusion nucléaire, dont l'objectif est d'atteindre Q = 10 (dix fois plus d'énergie produite que consommée). Après la 1re mise en service, la machine sera mise à l'arrêt le temps de préparer la phase suivante (plasmas à puissance nominale), puis à la phase nucléaire et à la production d'énergie à l'horizon 2035. |
| Joint European Torus | Tokamak | 1989 | Q=0,65 (aujourd'hui le meilleur rapport entre puissance produite et puissance induite par la fusion nucléaire). | N/A | Plus grand Tokamak fonctionnel existant, fruit d'une collaboration entre différents laboratoires nationaux européens. Depuis 2004, subit des travaux de mise à jour dans le but d'augmenter ses capacités pour participer au développement du projet ITER. |
| MAST-U (en) | Tokamak sphérique | 2019 | record actuel du béta toroïdal à 38 % | N/A | Plus grand tokamak sphérique en fonctionnement aujourd'hui[39], en attendant que le NSTX-U (en) soit réparé. Ses fonctions actuelles sont de tester des configurations du divertor pour ITER |
| Wendelstein 7-X | Stellarator | 2015 | En phase de test - les premiers résultats montrent que les spécifications du cahier des charges sont atteintes. | N/A |
|
| Z machine | Striction axiale | 2010 | Fusion réalisée en 2014[40]. Température trois fois inférieure à celle d'ITER. | Taux de réaction 10 000 fois trop faible pour obtenir un rendement Q>1 | Programme privé américain développé par Lockheed Martin dans les laboratoires de sa filiale Sandia (soucis de confidentialité). C'est un simulateur dont les expériences de fusion ne représentent qu'une partie de son utilité. |
| CFR (en) | Piège magnétique | N/A | Avancées théoriques. Compacité potentielle du système. | Avancées floues, pas de prototype fonctionnel | Programme privé américain. Lockheed Martin cherche à mettre au point un prototype à court terme. |
| Laser Mégajoule | Confinement laser | 2014 | N/A | Financement | L'objectif premier est d'être un simulateur permettant de remplacer les essais nucléaires conventionnels. Produire de l'énergie n'est qu'un axe secondaire de recherche. |
| National Ignition Facility | Confinement laser | NC | NC | NC |
Records
Température atteinte
- T-3 (
 Union soviétique), ~10 millions de degrés Celsius (1968)[41]
Union soviétique), ~10 millions de degrés Celsius (1968)[41] - TFTR (
 États-Unis), ~100 millions de degrés Celsius (1985)
États-Unis), ~100 millions de degrés Celsius (1985) - TFTR (
 États-Unis), ~510 millions de degrés Celsius (1995)[42]
États-Unis), ~510 millions de degrés Celsius (1995)[42] - JT-60 (
 Japon), ~522 millions de degrés Celsius (1996)[43]
Japon), ~522 millions de degrés Celsius (1996)[43] - JET (
 Royaume-Uni), ~325 millions de degrés (1997)[44]
Royaume-Uni), ~325 millions de degrés (1997)[44] - KSTAR (
 Corée du Sud), ~100 millions de degrés Celsius (20 sec, 2020)[45],[46]
Corée du Sud), ~100 millions de degrés Celsius (20 sec, 2020)[45],[46]
Temps d'entretien du plasma
- T-3 (
 Union soviétique), 20 millisecondes (1968)[47].
Union soviétique), 20 millisecondes (1968)[47]. - Tore Supra (
 France), 4 minutes 25 sec (2002)
France), 4 minutes 25 sec (2002) - Tore Supra (
 France), 6 minutes 30 secondes (4 décembre 2003)[48]
France), 6 minutes 30 secondes (4 décembre 2003)[48]
Puissance fusion nucléaire
- JET (
 Royaume-Uni), 16 MW (1 sec, octobre 1997)[49]
Royaume-Uni), 16 MW (1 sec, octobre 1997)[49]
Plasmas de fusion
À la température à laquelle la fusion est susceptible de se produire, la matière est à l’état de plasma.
Il s’agit d’un état particulier de la matière première dans lequel les atomes ou les molécules forment un gaz ionisé.
Un ou plusieurs électrons du nuage électronique qui entoure chaque noyau ont été arrachés, laissant des ions chargés positivement et des électrons libres, l’ensemble étant électriquement neutre.
Dans un plasma thermique, la grande agitation des ions et des électrons produit de nombreuses collisions entre les particules. Pour que ces collisions soient suffisamment violentes et entraînent une fusion, trois grandeurs interviennent : la température T, la densité N et le temps de confinement τ.
Le critère de Lawson établit que le rapport entre l’énergie produite et l’énergie perdue doit atteindre un certain seuil pour que le système soit rentable. L’ignition se produit à un stade plus élevé de production d’énergie[Passage contradictoire], encore impossible à créer dans les réacteurs actuels. Il s’agit du seuil à partir duquel la réaction est capable de s’auto-entretenir. Pour la réaction deutérium-tritium, ce seuil est de 1014 s/cm3[50].
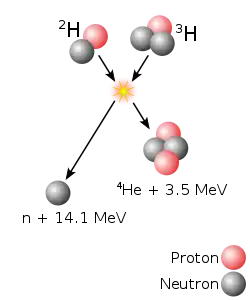
Analyse de la réaction deutérium plus tritium
L’énergie de liaison des constituants provient de la force d’interaction nucléaire forte, l’une des quatre forces d’interaction fondamentales de l’Univers.
Or, l’investissement énergétique à fournir pour obtenir cette liaison est proportionnel au produit des charges électriques des deux noyaux atomiques en présence. C’est pourquoi le choix pour la fusion s’est porté sur le deutérium et le tritium, deux isotopes lourds de l’hydrogène, pour lesquels ce produit vaut 1.
L’énergie minimale à fournir pour obtenir une fusion est de 4 keV (équivalent à une température de 40 millions de kelvins) ; l’énergie cinétique libérée est alors de 17,6 MeV, répartie pour 80 % dans le neutron émis et pour 20 % dans l’hélium 4 produit.
Mais l’énergie nécessaire pour atteindre le critère de Lawson et un rendement suffisamment positif se situe vers 10 keV soit 100 millions de degrés Celsius.
La réaction « deutérium + tritium » se traduit par une émission de neutrons rapides. Ces neutrons sont impossibles à confiner électromagnétiquement car ils ont une charge électrique nulle. Ils sont donc susceptibles d’être capturés par les noyaux d’atomes de la paroi de l’enceinte, qu’ils transmutent parfois en isotopes radioactifs (phénomène d’activation). L’activation peut à son tour s’accompagner de production de noyaux d’hélium, susceptibles de fragiliser les matériaux de structure. Elle pourrait compliquer l’usage industriel de la fusion et fait l’objet d’études avec différentes propositions de solutions (par exemple, des parois en matériaux composites, ou en alliages spécifiques de fer), mais elles nécessitent des études expérimentales difficiles à réaliser à court terme.
Les réactions générant des neutrons ne sont donc pas totalement « propres », mais sont toutefois nettement moins[Combien ?] génératrices de déchets que les réactions de fission nucléaire et la durée de vie de ces déchets est bien inférieure[Combien ?] à celle des produits radioactifs créés dans les centrales à fission nucléaire.
Approvisionnement en deutérium
Le deutérium est naturellement présent en grandes quantités dans les océans, à hauteur de 33 g/m3[51],[52]. Ces ressources théoriques permettraient de satisfaire la consommation d'énergie de l'espèce humaine pendant des millions d'années[53]. En effet, le deutérium contenu dans 1 m3 d'eau peut potentiellement fournir autant d'énergie que la combustion de 668 t de pétrole[54].
Le procédé d'extraction, la séparation isotopique de l'eau lourde par procédé de Girdler, est déjà industrialisé.
Approvisionnement en tritium
Le tritium est très rare dans la nature, avec environ un atome de tritium pour 1018 atomes d'hydrogène, soit 3,5 kg dans le monde[55]. Il doit donc être préparé artificiellement et assez rapidement utilisé, car sa nature d’isotope radioactif à courte durée de demi-vie fait que la moitié du tritium naturel ou artificiel produit disparaît en 12,3 ans. De plus, il est difficile à confiner, car c'est un atome si petit qu'il percole dans l'acier et peut le traverser.
- Le tritium est actuellement produit par les centrales nucléaires (filières CANDU majoritairement) mais il pourrait rapidement manquer (en quelques décennies dès les phases d'expérimentation et premières applications)[56].
- Une autre voie de production, choisie pour l'approvisionnement du projet ITER, est l'irradiation neutronique de lithium 6 suivant la réaction 6
3Li + 1
0n ⟶ 3
1T + 4
2He. Le neutron nécessaire est d'une énergie de l'ordre de 2,5 MeV, inférieure à celle des neutrons de fusion (14 MeV). Les réserves mondiales de lithium, estimées à 9,5 millions de tonnes sous forme de minerai, suffiraient théoriquement à garantir plus d'un million d'années de fonctionnement[53],[57]. - Enfin, une troisième voie de production pourrait être la régénération du tritium au cours de sa réaction de fusion. Toutefois, le bilan neutronique de celle-ci ne lui permet pas de produire son propre combustible :
- chaque réaction de fusion consomme un atome de tritium et produit un neutron de forte énergie qui peut être dédoublé par spallation s'il bombarde un atome lourd ;
- la production d'un atome de tritium à partir du lithium 6 nécessite un neutron.
- Pour boucler le cycle de régénération du tritium, il faudrait donc qu'au moins un neutron sur deux produit dans le réacteur à fusion dédoublé par spallation convertisse deux atomes de 6Li en tritium ; ceci semble irréaliste. Le fonctionnement des réacteurs de fusion D + T n'est donc pas capable à lui seul d'assurer l'approvisionnement en tritium.
Applications
Si la fusion a pu être utilisée dans le domaine militaire avec les bombes H, il n’existe pas encore d’application civile pour la production d'électricité. Seuls des prototypes d’étude ont pu être construits, cf. section #État d'avancement des projets.
Il existe quelques autres usages, comme les générateurs de neutrons.
Réactions de fusion importantes
Chaînes de réactions en astrophysique
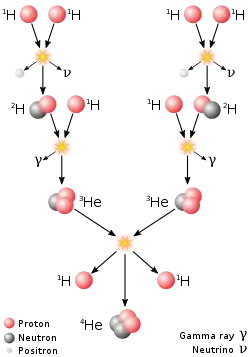 |
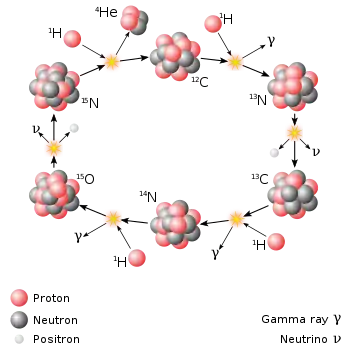 | |
La branche PP1 de la chaîne proton-proton prédomine dans les étoiles d’une taille similaire ou inférieure à celle du Soleil. |
Le cycle carbone-azote-oxygène prédomine dans les étoiles de masse supérieure à celle du Soleil. |
Le processus de fusion le plus important dans la nature est celui qui alimente les étoiles. Le résultat net est la fusion de quatre protons en une particule alpha (noyau d’hélium 4), accompagnée de la libération de deux positrons, de deux neutrinos (qui transforment deux des protons en neutrons) et d’énergie, mais diverses réactions individuelles sont impliquées selon la masse de l’étoile. Dans les étoiles de taille similaire ou inférieure à celle du Soleil, la chaîne proton-proton prédomine. Dans les étoiles plus lourdes, le cycle carbone-azote-oxygène (CNO) est le plus important. Les deux types de processus sont à l’origine de la création de nouveaux éléments dans le cadre de la nucléosynthèse stellaire. D'autres processus entrent en jeu dans les explosions d'étoiles massives en supernovas, qui mènent à la création d'éléments lourds, dans le cadre de la nucléosynthèse explosive.
Aux températures et densités du cœur des étoiles, le taux de réaction de fusion est notablement peu élevé. Par exemple, à la température (T ≈ 15 MK) et à la densité (160 g/cm3) du cœur du Soleil, le taux de libération d’énergie est seulement de 276 μW/cm3 — environ le quart du débit de chaleur par unité de volume d’un humain au repos[58]. Ainsi, la reproduction en laboratoire des conditions du cœur des étoiles à des fins de production d’énergie de fusion est totalement impossible à mettre en pratique. Les taux de réaction dépendant fortement de la température (exp(−E/kT)), il est nécessaire, pour atteindre des taux raisonnables de production d’énergie dans des réacteurs à fusion nucléaire, de travailler à des températures dix à cent fois plus élevées que celles du cœur des étoiles, soit T ≈ 0,1 à 1 GK (de l’ordre de cent millions à un milliard de kelvins).
Critères et candidats pour les réactions terrestres
Dans la fusion mise en œuvre par l’homme, rien n’impose que le combustible utilisé soit constitué de protons, et il est possible d’employer des températures plus élevées pour accéder à des réactions de plus grande section efficace. Cela implique une valeur plus faible du critère de Lawson, et donc moins d’efforts à produire pour le démarrage des réactions. La production de neutrons, qui constitue un sujet de préoccupation car elle entraine une activation radiologique de la structure du réacteur, possède en contrepartie l’avantage d’autoriser l’extraction de l’énergie de fusion ainsi que la production de tritium. Les réactions qui ne produisent pas de neutrons sont dites aneutroniques.
Pour être utilisable comme source d’énergie, une réaction de fusion doit satisfaire à plusieurs critères. Elle doit :
- être exothermique : cette condition semble évidente, mais elle limite les réactifs à la partie de la courbe des énergies de liaison correspondant aux faibles numéros atomiques Z (nombre de protons). Elle fait également de l’hélium 4He le produit le plus fréquent en raison de ses liaisons extrêmement étroites, bien que l’on rencontre également 3He et 3T ;
- impliquer des noyaux à Z faible : la répulsion électrostatique doit être vaincue pour que les noyaux puissent se rapprocher suffisamment pour fusionner ;
- avoir deux réactifs : à toutes les densités inférieures à celles des étoiles, la collision simultanée de trois particules est trop improbable. Dans le cas du confinement inertiel, on dépasse à la fois les densités et les températures stellaires, ce qui permet de compenser la faiblesse du troisième paramètre du critère de Lawson, la très brève durée de confinement ;
- avoir deux produits ou plus : ceci permet la conservation simultanée de l’énergie et de l’impulsion ;
- conserver à la fois les protons et les neutrons : les sections efficaces pour l’interaction faible sont trop petites.
Peu de réactions satisfont tous ces critères. Les suivantes sont celles dont les sections efficaces sont les plus grandes[59],[60] :
(1) 2
1D+ 3
1T⟶ 4
2He(3,52 MeV) + 1
0n (14,06 MeV)(2a) 2
1D+ 2
1D⟶ 3
1T(1,01 MeV) + 1
1p (3,02 MeV)50% (2b) ⟶ 3
2He(0,82 MeV) + 1
0n (2,45 MeV)50% (3) 2
1D+ 3
2He⟶ 4
2He(3,6 MeV) + 1
1p (14,7 MeV)(4) 3
1T+ 3
1T⟶ 4
2He+ 1
0n + 1
0n+ 11,3 MeV (5) 3
2He+ 3
2He⟶ 4
2He+ 1
1p + 1
1p+ 12,9 MeV (6a) 3
2He+ 3
1T⟶ 4
2He+ 1
1p + 1
0n+ 12,1 MeV 57% (6b) ⟶ 4
2He(4,8 MeV) + 2
1D (9,5 MeV)43% (7a) 2
1D+ 6
3Li⟶ 4
2He+ 4
2He+ 22,4 MeV (7b) ⟶ 3
2He+ 4
2He + 1
0n+ 2,56 MeV (7c) ⟶ 7
3Li+ 1
1p+ 5,0 MeV (7d) ⟶ 7
4Be+ 1
0n+ 3,4 MeV (8) 1
1p+ 6
3Li⟶ 4
2He(1,7 MeV) + 3
2He (2,3 MeV)(9) 3
2He+ 6
3Li⟶ 4
2He+ 4
2He + 1
1p+ 16,9 MeV (10) 1
1p+ 11
5B⟶ 4
2He+ 4
2He + 4
2He+ 8,7 MeV.
Pour les réactions avec deux produits, l’énergie est répartie entre eux en proportion inverse de leurs masses, comme indiqué. Dans la plupart des réactions avec trois produits, la distribution des énergies est variable. Pour les réactions qui peuvent donner naissance à plus d’un ensemble de produits, les proportions sont indiquées. Certaines réactions candidates peuvent être éliminées immédiatement[61]. La réaction D-6Li ne présente aucun avantage par rapport à p-11B car, si elle est pratiquement aussi difficile à déclencher, elle produit considérablement plus de neutrons à travers des réactions 2D-2D annexes. Il existe également une réaction p-7Li, cependant sa section efficace est bien trop faible, sauf peut-être quand Ti > 1 MeV, mais à de telles températures une réaction endothermique, produisant directement des neutrons, devient très significative. Il existe enfin une réaction p-9Be, qui non seulement est difficile à déclencher, mais dans laquelle 9Be peut être aisément amené à se scinder en deux alphas et un neutron.
Outre les réactions de fusion, les réactions suivantes impliquant des neutrons sont importantes pour la production de tritium dans les bombes à fusion « sèches » et certains réacteurs en projet :
Pour évaluer l’utilité de ces réactions, outre les réactifs, les produits, et l’énergie libérée, on doit aussi disposer d’informations sur la section efficace. Tout dispositif de fusion possède une pression maximale qu’il est capable de maintenir, et un dispositif économique devra toujours travailler à proximité de ce maximum. Cette pression étant donnée, l’énergie de fusion maximale est obtenue en choisissant une température telle que <σv>/T2 soit maximal. C’est aussi la température à laquelle la valeur du triple produit nTτ requise pour l’ignition est minimale, cette dernière étant inversement proportionnelle à <σv>/T2 (voir critère de Lawson). Cette température optimale ainsi que la valeur de <σv>/T2 à cette température sont données pour quelques-unes de ces réactions dans la table suivante.
| Combustible | T [keV] | <σv>/T2 [m3 s−1 keV−2] |
|---|---|---|
| 2D-3T | 13,6 | 1,24 × 10−24 |
| 2D-2D | 15 | 1,28 × 10−26 |
| 2D-3He | 58 | 2,24 × 10−26 |
| p+-6Li | 66 | 1,46 × 10−27 |
| p+-11B | 123 | 3,01 × 10−27 |
Nombre de ces réactions forment des chaines. Par exemple, un réacteur alimenté en 3T et 3He crée un peu de 2D, qu’il est alors possible d’utiliser dans la réaction 2D + 3He si les énergies sont « correctes ». Une idée élégante consiste à combiner les réactions (8) et (9). 3He produit par la réaction (8) est susceptible de réagir avec 6Li produit par la réaction (9), avant sa thermalisation complète. On produit ainsi un proton qui à son tour peut subir la réaction (8) avant thermalisation. Une analyse détaillée montre que cette idée ne fonctionnera en fait pas très bien, mais c’est un bon exemple d’un cas où l’hypothèse habituelle d’un plasma maxwellien n’est pas appropriée.
Neutronicité, exigences en confinement et densité de puissance
N’importe laquelle des réactions ci-dessus peut en principe être à la base de la production d’énergie de fusion. Outre la température et la section efficace abordées plus haut, il est nécessaire d'examiner l’énergie totale des produits de fusion Efusion, l’énergie des produits de fusion électriquement chargés Ech, et le numéro atomique Z des réactifs autres que les isotopes de l’hydrogène.
Cependant, la spécification de la réaction 2D-2D entraine certaines difficultés. Tout d’abord, il faut effectuer une moyenne sur les deux branches (2i) et (2ii). Il faut ensuite, ce qui est plus difficile, décider comment traiter les produits 3T et 3He. 3T « brûle » si bien dans un plasma de deutérium qu’il est pratiquement impossible de l’en extraire. La réaction 2D-3He est optimale à une température bien plus élevée et la combustion à la température optimale pour 2D-2D peut être faible ; il semble donc raisonnable de supposer que 3T va brûler, mais pas 3He, et que l’énergie ainsi libérée va s’ajouter à celle de la réaction. L’énergie de fusion 2D-2D sera donc Efusion = (4,03 +17,6 + 3,27) / 2 = 12,5 MeV, et celle des particules chargées Ech = (4,03 + 3,5 + 0,82) / 2 = 4,2 MeV.
Un autre aspect spécifique de la réaction 2D-2D tient à la présence d’un seul réactif, ce que l’on doit prendre en compte lors du calcul du taux de réaction.
En se fondant sur ces choix, les paramètres de quatre des réactions les plus importantes sont présentés dans la table suivante.
| Combustible | Z | Efusion [MeV] | Ech [MeV] | Neutronicité |
|---|---|---|---|---|
| 2D-3T | 1 | 17,6 | 3,5 | 0,80 |
| 2D-2D | 1 | 12,5 | 4,2 | 0,66 |
| 2D-3He | 2 | 18,3 | 18,3 | ~0,05 |
| p+-11B | 5 | 8,7 | 8,7 | ~0,001 |
La dernière colonne correspond à la neutronicité de la réaction, définie comme la fraction de l’énergie de fusion libérée sous forme de neutrons. C’est un indicateur important de l’ampleur des problèmes associés aux neutrons, tels que les dommages provoqués par les radiations, la protection biologique, la télémanipulation et la sécurité. Pour les deux premières réactions, elle est donnée par (Efusion - Ech)/Efusion. Pour les deux dernières, où cette formule donnerait un résultat égal à 0, les valeurs indiquées sont des estimations grossières basées sur des réactions annexes qui produisent des neutrons dans un plasma en équilibre thermique.
Il est nécessaire de mélanger les réactifs dans les proportions optimales. C’est le cas lorsque chaque ion de réactif et ses électrons associés participent pour moitié à la pression. En supposant que la pression totale est fixée, cela signifie que la densité des ions non hydrogène est plus faible que celle des ions hydrogène d’un facteur 2/(Z+1). En conséquence, le taux de ces réactions est réduit du même facteur, ce qui constitue la différence la plus importante dans les valeurs de <σv>/T2. D’autre part, comme la réaction 2D-2D n’a qu’un seul réactif, le taux est deux fois plus élevé que si le combustible était constitué de deux isotopes d’hydrogène.
Il existe donc une « pénalité » de (2/(Z+1)) pour les combustibles autres que l’hydrogène, provenant du fait qu’ils ont besoin de plus d’électrons, ce qui absorbe de la pression sans participer à la réaction de fusion. Il est généralement correct de supposer que la température électronique et la température ionique sont pratiquement égales. Certains auteurs envisagent que les électrons puissent être maintenus à une température nettement inférieure à celle des ions. Dans de telles situations, connues sous le nom de « modes à ions chauds », la « pénalité » ne s'appliquerait pas. Il existe de la même façon un « bonus » d’un facteur 2 pour la réaction 2D-2D dû au fait que chaque ion peut réagir avec n’importe lequel des autres ions, et pas seulement avec une fraction d’entre eux.
La table suivante permet de comparer ces réactions.
| Combustible | <σv>/T2 | Pénalité/bonus | Réactivité | Critère de Lawson | Densité de puissance (W m−3 kPa−2) | Rapport de densité de puissance |
|---|---|---|---|---|---|---|
| 2D-3T | 1,24 × 10−24 | 1 | 1 | 1 | 34 | 1 |
| 2D-2D | 1,28 × 10−26 | 2 | 48 | 30 | 0,5 | 68 |
| 2D-3He | 2,24 × 10−26 | 2/3 | 83 | 16 | 0,43 | 80 |
| p+-6Li | 1,46 × 10−27 | 1/2 | 1 700 | 0,005 | 6 800 | |
| p+-11B | 3,01 × 10−27 | 1/3 | 1 240 | 500 | 0,014 | 2 500 |
La valeur maximale de <σv>/T2 est reprise d’une table précédente. Le facteur « pénalité/bonus » est celui lié soit à un réactif non hydrogène, soit à une réaction sur une espèce unique. Les valeurs de la colonne « réactivité » sont obtenues en divisant 1,24 × 10−24 par le produit des deuxième et troisième colonnes ; chaque valeur indique le facteur de ralentissement des réactions par rapport à la réaction 2D-3T dans des conditions comparables. La colonne « critère de Lawson » pondère ces résultats par Ech et donne une indication de la difficulté d’atteindre l’ignition avec ces réactions, par rapport à la réaction 2D-3T. La dernière colonne, étiquetée « densité de puissance », pondère la réactivité pratique par Efusion ; elle donne le facteur de réduction de la densité de puissance de fusion pour une réaction particulière par rapport à la réaction 2D-3T, et peut être considérée comme une mesure du potentiel économique.
Pertes par Bremsstrahlung dans les plasmas quasi-neutres isotropes
Les ions subissant la fusion ne le font quasiment jamais de façon isolée, mais sont mélangés à des électrons qui neutralisent la charge électrique des ions en formant un plasma. Les électrons ayant généralement une température comparable ou supérieure à celle des ions, ils entrent en collision avec ceux-ci et émettent des rayons X dont l'énergie est de l'ordre de 10 à 30 keV (Bremsstrahlung ou rayonnement de freinage). Le Soleil et les étoiles sont opaques aux rayons X, mais la plupart des réacteurs de fusion terrestre ont une épaisseur optique faible pour les X de cette gamme d'énergie. La réflexion des rayons X est difficile à obtenir, mais ils sont absorbés (et convertis en chaleur) par une épaisseur de moins d'1 mm d'acier inoxydable (qui fait partie du blindage d'un réacteur). Le rapport entre la puissance de fusion produite et ces pertes est un critère de qualité important de la réaction. La valeur maximale de ce rapport est généralement obtenue à une température bien plus élevée que celle qui rend la densité de puissance maximale (voir le sous-chapitre précédent). La table suivante montre la température optimale approximative ainsi que le rapport de puissance à cette température pour plusieurs réactions.
| Combustible | Ti (keV) | Pfusion/PBremsstrahlung |
|---|---|---|
| 2D-3T | 50 | 140 |
| 2D-2D | 500 | 2,9 |
| 2D-3He | 100 | 5,3 |
| 3He-3He | 1 000 | 0,72 |
| p+-6Li | 800 | 0,21 |
| p+-11B | 300 | 0,57 |
Il est probable que les véritables rapports entre puissance de fusion et puissance de Bremsstrahlung sont notablement plus faibles, et ce pour diverses raisons. En premier lieu, les calculs supposent que l’énergie des produits de fusion est entièrement transmise aux ions du combustible, qui la perdent ensuite par collision au profit des électrons, qui à leur tour perdent de l’énergie par Bremsstrahlung. Cependant, comme les produits de fusion ont une vitesse bien plus grande que les ions du combustible, ils abandonnent une partie significative de leur énergie directement aux électrons. En deuxième lieu, le plasma est supposé ne comporter que des ions de combustible. En pratique, il existe une proportion significative d’ions d’impuretés, qui vont faire diminuer le rapport. En particulier, les produits de fusion eux-mêmes doivent demeurer dans le plasma jusqu’à ce qu’ils aient abandonné leur énergie, et y resteront encore quelque temps, quel que soit le procédé de confinement envisagé. En dernier lieu, tous les canaux de perte d’énergie autres que le Bremsstrahlung ont été considérés comme négligeables. Les deux derniers facteurs sont apparentés. Sur les plans théorique et expérimental, le confinement des particules et le confinement de l’énergie semblent étroitement apparentés. Dans un procédé de confinement qui retient efficacement l’énergie, les produits de fusion vont s’accroître. Si les produits de fusion sont expulsés efficacement, alors le confinement énergétique sera médiocre.
Les températures pour lesquelles le rapport entre puissances de fusion et de Bremsstrahlung est maximal sont dans tous les cas plus élevées que celles pour lesquelles la densité de puissance est maximale et le triple produit de fusion minimal. Cela ne change pas beaucoup le point de fonctionnement optimal pour 2D-3T car la part de Bremsstrahlung est faible, mais cela pousse les autres combustibles vers des régimes où la densité de puissance relativement à 2D-3T est encore plus faible, et le confinement requis encore plus difficile à obtenir. Pour 2D-2D et 2D-3He, les pertes par Bremsstrahlung constituent un problème sérieux, peut-être même bloquant. Pour 3He-3He, p+-6Li et p+-11B, les pertes par Bremsstrahlung paraissent rendre impossible la réalisation d’un réacteur à fusion utilisant ces combustibles avec un plasma quasi-neutre isotrope[62]. Cette limitation ne s'applique ni aux plasmas non neutres, ni aux plasmas anisotropes[réf. nécessaire], qui ont cependant leurs propres défis à relever.
Sécurité
De nombreuses difficultés sont à relever en ce qui concerne la fiabilité et la sécurité pour un fonctionnement sur le long terme. Elles varient selon le type de réacteur.
Elles concernent notamment :
- le confinement magnétique qui doit être constant ;
- la gestion de températures et pression très élevées ;
- la gestion du tritium dans les filières en produisant et consommant ;
- les risques combinés de corrosion et radiolyse pour les solutions fonctionnant à température et/ou pression élevée[63]. De nouvelles modalités de test d'effort et de résistance des matériaux doivent être inventées pour simuler les conditions régnant à l'intérieur de ce type de réacteurs[64] ;
- le risque sismique et de tsunami.
Formations universitaires
Après la décision prise en 2006 de réaliser le projet ITER en France, plusieurs institutions françaises d'enseignement supérieur se sont jointes en une fédération de « Formation aux Sciences de la Fusion »[65]. Cette formation vise à préparer des scientifiques et des ingénieurs de très haut niveau, français ou étrangers, aptes à s'investir dans les programmes concernant les recherches sur les plasmas, la fusion et l'énergie. En particulier dans l'exploitation scientifique et technique de grands équipements associés. La spécialité de master couvre donc tous les domaines scientifiques et technologiques concernant les milieux ionisés par les approches théoriques, de simulation et d'expérimentation et propose un enseignement multidisciplinaire sur les plasmas, dans toute leur variété, les matériaux sous irradiation, la cryotechnologie et la supraconductivité, les chauffages de très haute puissance par microondes ou lasers et l'instrumentation en milieu extrême. La formation se fait au travers de trois parcours : deux portent essentiellement sur la physique (fusion par confinement magnétique et plasmas magnétisés d'une part, fusion par confinement inertiel et plasmas denses d'autre part), un troisième parcours est à contenu plus technologique et embrasse la physique et les technologies des plasmas et de la fusion.
Avec la fusion de certaines universités, huit établissements, répartis sur quatre sites du territoire français, sont cohabilités pour délivrer ce diplôme, avec des enseignements qui ont lieu en parallèle dans ces sites et lors de regroupement des étudiants à Cadarache et Bordeaux :
- université d'Aix-Marseille, École centrale de Marseille en région PACA ;
- université de Bordeaux en Nouvelle-Aquitaine ;
- université de Lorraine, Faculté des sciences à Nancy ;
- université Pierre-et-Marie-Curie (Paris 6), université Paris-Sud (Paris 11), École polytechnique (ParisTech), INSTN pour l'Île-de-France.
Quatre écoles d'ingénieur sont également associées :
- École centrale Paris ;
- Supélec ;
- SupOptique (ParisTech) ;
- ENSAM (ParisTech).
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Nuclear fusion » (voir la liste des auteurs).
Notes
- Cette confusion semble avoir été faite par de nombreux journalistes les premiers jours de l'accident de la centrale nucléaire de Fukushima Daiichi, ainsi que par Michèle Rivasi, experte auprès d'Europe Écologie Les Verts pour les questions de radioactivité (sur Europe 1 le , pendant l'émission Europe matin).
Références
- Benuzzi-Mounaix 2008, p. 21.
- Benuzzi-Mounaix 2008, p. 36.
- Laurent Sacco, « Une énigme quantique avec l'effet tunnel a été résolue », sur Futura (consulté le ).
- Benuzzi-Mounaix 2008, p. 22.
- Benuzzi-Mounaix 2008, p. 51.
- Benuzzi-Mounaix 2008, p. 52.
- (en) « L'avènement des tokamaks », sur ITER (consulté le ).
- « la crise des années 1970-1990 », sur Encyclopédie Larousse en ligne (consulté le ).
- (en) « History of Fusion », sur EUROfusion (consulté le ).
- « La fusion sur Terre : histoire de la fusion », sur Futura (consulté le ).
- (en) Bellan Paul M, Spheromaks : A Practical Application Of Magnetohydrodynamic Dynamos And Plasma Self-organization, World Scientific, -, , 356 pages p., p. 11-13
- (en) Pierre-Alexandre Gourdain, « Is the Troyon limit a beta limit? », Physics of Plasmas, .
- « Nucléaire : nouveau surcoût de 4 milliards pour le projet ITER », sur Les Échos, (consulté le ).
- A Sykes, R Akers, L Appel et P G Carolan, « High- performance of the START spherical tokamak », Plasma Physics and Controlled Fusion, vol. 39, no 12B, , B247–B260 (ISSN 0741-3335 et 1361-6587, DOI 10.1088/0741-3335/39/12B/019, lire en ligne, consulté le )
- (en) « Stellarators - an overview », sur ScienceDirect (consulté le ).
- (en) R. C. Wolf, A. Ali, A. Alonso et J. Baldzuhn, « Major results from the first plasma campaign of the Wendelstein 7-X stellarator », Nuclear Fusion, vol. 57, no 10, , p. 102020 (ISSN 0029-5515, DOI 10.1088/1741-4326/aa770d, lire en ligne, consulté le )
- R. C. Wolf, A. Alonso, S. Äkäslompolo et J. Baldzuhn, « Performance of Wendelstein 7-X stellarator plasmas during the first divertor operation phase », Physics of Plasmas, vol. 26, no 8, , p. 082504 (ISSN 1070-664X, DOI 10.1063/1.5098761, lire en ligne, consulté le )
- « L’assemblage du réacteur du projet international ITER est lancé, près de 15 ans après ses débuts », Le Monde, (consulté le ).
- « Fusion nucléaire contrôlée : au Royaume-Uni, les chercheurs avancent à grands pas », sur L'EnerGeek, (consulté le ).
- Thomas Burgel, « La fusion nucléaire fait un bond en avant », sur korii., (consulté le ).
- (en) Elizabeth Gibney, « UK hatches plan to build world's first fusion power plant », Nature, , d41586–019–03039-9 (ISSN 0028-0836 et 1476-4687, DOI 10.1038/d41586-019-03039-9, lire en ligne, consulté le ).
- Nathalie Mayer, « Fusion nucléaire : la Chine a allumé son « soleil artificiel » », sur Futura, (consulté le ).
- Définitions lexicographiques et étymologiques de « fusion » (sens C4) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- ITER Physics Basis Editors, ITER Physics Expert Group Chairs an Co-Chairs et ITER Joint Central Team and Physics Unit, « Chapter 1: Overview and summary », Nuclear Fusion, vol. 39, no 12, , p. 2137–2174 (ISSN 0029-5515, DOI 10.1088/0029-5515/39/12/301).
- J.E. Menard, T. Brown, L. El-Guebaly et M. Boyer, « Fusion nuclear science facilities and pilot plants based on the spherical tokamak », Nuclear Fusion, vol. 56, no 10, , p. 106023 (ISSN 0029-5515 et 1741-4326, DOI 10.1088/0029-5515/56/10/106023, lire en ligne, consulté le ).
- Melanie Windridge, « Smaller and quicker with spherical tokamaks and high-temperature superconductors », Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 377, no 2141, , p. 20170438 (PMID 30967052, PMCID PMC6365856, DOI 10.1098/rsta.2017.0438, lire en ligne, consulté le ).
- (en-GB) Amit Lakhani, « System Studies of Spherical Tokamaks », sur UKAEA Scientific Publications (consulté le ).
- Allen H. Boozer, « What is a stellarator? », Physics of Plasmas, vol. 5, no 5, , p. 1647–1655 (ISSN 1070-664X et 1089-7674, DOI 10.1063/1.872833).
- (en) Alessandro Lampasi, Giuseppe Maffia, Franco Alladio et Luca Boncagni, « Progress of the plasma centerpost for the PROTO-SPHERA spherical tokamak », Energies, vol. 9, no 7, , p. 508 (ISSN 1996-1073, DOI 10.3390/en9070508).
- « Proto-Sphera Homepage », ENEA (consulté le ).
- (en-US) Bryson Masse, « This Vancouver startup is chasing the dream of clean, limitless energy forever », sur Motherboard, Vice Media, (consulté le ).
- Fusion nucléaire : Jeff Bezos soutient le projet d'une première centrale près de Londres, Les Échos, 17 juin 2021.
- Loren C. Steinhauer, « Review of field-reversed configurations », Physics of Plasmas, vol. 18, no 7, , p. 070501 (ISSN 1070-664X, DOI 10.1063/1.3613680, lire en ligne, consulté le )
- (en) M. Tuszewski, « Field reversed configurations », Nuclear Fusion, vol. 28, no 11, , p. 2033–2092 (ISSN 0029-5515, DOI 10.1088/0029-5515/28/11/008, lire en ligne, consulté le ).
- (en) O.A Hurricane et al., Fuel gain exceeding unity in an inertially confined fusion implosion, Nature, 2014 (13008)
- (en) We're one step closer to nuclear fusion energy, Wired.co.uk, février 2014.
- (en) Sandia’s Z machine exceeds two billion degrees Kelvin, sur sandia.gov, 8 mars 2006 (consulté le 7 juin 2016).
- « ITER Mag - Objectif 2025 », sur www.iter.org, (consulté le ).
- J.R. Harrison, R.J. Akers, S.Y. Allan et J.S. Allcock, « Overview of new MAST physics in anticipation of first results from MAST Upgrade », Nuclear Fusion, vol. 59, no 11, , p. 112011 (ISSN 0029-5515 et 1741-4326, DOI 10.1088/1741-4326/ab121c, lire en ligne, consulté le )
- (en) M.R. Gomez, S.A. Slutz, A.B. Sefkow et al., « Experimental Demonstration of Fusion-Relevant Conditions in Magnetized Liner Inertial Fusion », Physical Review Letters, vol. 113, no 15, , p. 5 (DOI 10.1103/PhysRevLett.113.155003, lire en ligne, consulté le ).
- (en) The JET Team presented by J. Jacquinot (initialement publié in J Jacquinot and the JET team, « Deuterium-tritium operation in magnetic confinement experiments: results and underlying physics », Plasma Physics and Controlled Fusion, vol. 41, no 3A, ), « Deuterium-Tritium Operation in Magnetic Confinement Experiments: Results and Underlying Physics », sur EUROfusion,
- « L'avènement des tokamaks », ITER Mag, no 11, (lire en ligne, consulté le ).
- Sylvie Briet, « Iter : l'Europe accélère », sur Libération, (consulté le ).
- Voir Critère de Lawson#Exemple sur la configuration deutérium-tritium.
- Georges Vendryes, « Les ressources énergétiques de la fission et de la fusion nucléaires », (consulté le ).
- « Les combustibles », sur ITER (consulté le ).
- David J. C. MacKay (trad. Association AMIDES), « Du nucléaire ? », dans L’énergie durable — Pas que du vent ! [« Sustainable Energy – without the hot air »], De Boeck, , 443 p. (ISBN 978-0-9544529-3-3 et 978-1-906860-01-1, amides.fr, lire en ligne [PDF]), p. 204.
- Aurélie, « L'énergie du futur : (ITER), fusion, loi de décroissance radioactive (bac S Inde 2009) », sur www.chimix.com, (consulté le ).
- « Livre blanc du tritium », sur Autorité de sûreté nucléaire, (consulté le ).
- (en) Scott Willms, « Tritium Supply Considerations » [« Considérations sur la fourniture de tritium »], Fusion Development Paths Workshop, Los Alamos National Laboratory, (lire en ligne [PDF], consulté le ).
- Jean-Louis Boutard, « Réacteurs de fusion : le défi majeur des matériaux », Reflets de la physique, no 38, , p. 22–27 (ISSN 1953-793X et 2102-6777, DOI 10.1051/refdp/201438022, lire en ligne, consulté le )
- (en) « From Core to Corona : Layers of the Sun », sur FusEdWeb - Fusion Education, Lawrence Livermore National Laboratory (consulté le ).
- (en) M. Kikuchi, K. Lackner et M. Q. Tran, Fusion Physics, AIEA, 2012, p. 22. (ISBN 978-92-0-130410-0)
- (en) K. Miyamoto, Plasma Physics and Controlled Nuclear Fusion, Springer-Verlag, 2005. (ISBN 3-540-24217-1)
- « Non trouvé le 7 juin 2016 »(Archive • Wikiwix • Archive.is • Google • Que faire ?), sur mit.edu.
- Diverses solutions possibles à ce dilemme sont envisagées - et rejetées - dans ce document : Todd Rider, Fundamental limitations on plasma fusion systems not in thermodynamic equilibrium.
- (en) A. Bruggeman, M. Snykers, W.F. Bogaerts, R. Waeben, M.J. Embrechts et D. Steiner, « Radiolysis and corrosion aspects of the aqueous self-cooled blanket concept », Fusion Engineering and Design, vol. 8, , p. 133-137 (DOI 10.1016/S0920-3796(89)80097-3, résumé).
- (en) D.J. Duquette, K.L. Wrisley1, E. Coomer et D. Steiner, « Corrosion behavior of stainless steels in aqueous salt blanket option solutions for ITER », Journal of Nuclear Materials, vol. 191-194, , p. 992-996 (DOI 10.1016/0022-3115(92)90623-S, résumé).
- Fédération regroupant les masters en science des plasmas et de la fusion, sur Fédération Sciences plasama fusion (consulté le ).
Voir aussi
Bibliographie
- Alessandra Benuzzi-Mounaix, La fusion nucléaire : Un espoir pour une énergie propre et inépuisable, Paris, Belin - Pour la science, coll. « Bibliothèque scientifique », , 127 p. (ISBN 978-2-7011-4724-6).

- (en) Cornelius Marius Braams et Peter E. Stott, Nuclear Fusion, New York, CRC Press, (ISBN 978-0-7503-0705-5, lire en ligne)
- (en) Stefano Atzeni et Jürgen Meyer-ter-Vehn, The physics of inertial fusion : beam plasma interaction, hydrodynamics, hot dense matter, Oxford, Oxford University Press, , 458 p. (ISBN 978-0-19-856264-1, lire en ligne)
Articles connexes
- Énergie nucléaire
- Fusion par confinement magnétique
- Fusion par confinement inertiel
- Fusion aneutronique
- ITER (International Thermonuclear Experimental Reactor)
- Arme à fusion pure
- Fusion froide
- Nucléosynthèse
- Physique des plasmas
- Procédé COLEX
- Centre d'étude de l'énergie nucléaire
- Agence internationale de l'énergie atomique
- TAE Technologies (en)
Liens externes
- « Fusion nucléaire : la quête du Graal », La Méthode scientifique, France Culture, 31 août 2021.
- « Fusion nucléaire : l’énergie à profusion », La Méthode scientifique, France Culture, 12 juin 2019.
- Fusion magnétique, dossier du CEA.
- Portail de la physique
- Portail de l’astronomie
- Portail du nucléaire
- Portail de l’énergie