Numération grecque
La numération grecque de l'Antiquité était double : on pouvait écrire les chiffres et les nombres soit au moyen de signes dits « acrophoniques » correspondant grosso modo à la première lettre de leur nom en grec ancien, soit au moyen de lettres, comme en numération hébraïque ou arabe. On connaît également un système de numération scientifique, inspiré des mathématiques babyloniennes. Actuellement, ce sont les chiffres arabes que l'on utilise le plus fréquemment en Grèce.

Numération acrophonique
Dès le Ve siècle av. J.-C., en Attique, région d'Athènes, apparaissent des chiffres dont chaque signe (à l'exception de celui pour 1) n'est autre que la première lettre du nom du nombre, tracée dans l'alphabet local athénien, lequel fut remplacé en -403 par l'alphabet ionien dans lequel certaines lettres ont changé de tracé et/ou de valeur (Voir Histoire de l'alphabet grec).
- Ι pour 1 (ΙΩΤΑ, ιώτα, iota) (comme on dirait un iota pour peu),
 pour 5 (ΠΕΝΤΕ, πέντε, pénte)[1] (comme le penta dans pentagone en français),
pour 5 (ΠΕΝΤΕ, πέντε, pénte)[1] (comme le penta dans pentagone en français),- Δ pour 10 (ΔΕΚΑ, δέκα, déka) (comme le déca dans décathlon, décamètre, ...),
- Η pour 100 (ΗΕΚΑΤΟΝ, ἑκατόν, hekatón)[2] (comme dans hectare),
- Χ pour 1 000 (ΧΙΛΙΟΙ, χίλιοι, khílioi) (comme dans kilogramme),
- Μ pour 10 000 (ΜΥΡΙΟΙ, μύριοι, múrioi) (comme dans myriade).
La notation des nombres suivait le principe additif que l'on retrouve dans les chiffres romains. Ainsi, 3 s'exprimait par ΙΙΙ, 9 par ΓΙΙΙΙ, 400 par ΗΗΗΗ, etc.
Il existait des signes notant des valeurs intermédiaires, représentés par une ligature des deux chiffres fondamentaux pour :
- 50 →
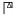 (Γ×Δ) ;
(Γ×Δ) ; - 500 →
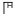 (Γ×Η) ;
(Γ×Η) ; - 5000 →
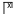 (Γ×Χ) ;
(Γ×Χ) ; - 50 000 →
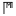 (Γ×Μ).
(Γ×Μ).
- 50 →
Chacun de ces nombres est composé du signe de valeur 5 auquel on a souscrit celui du multiplicateur.
Unicode réserve des emplacements spécifiques pour ces chiffres. On ne pourra les visualiser ci-dessous que si l'on utilise une police de caractères les contenant, comme ALPHABETUM Unicode, Cardo ou New Athena Unicode : 𐅃 (5), 𐅄 (50), 𐅅 (500), 𐅆 (5 000) 𐅇 (50 000).
Presque exclusivement attesté par des sources épigraphiques, ce système numéral était surtout utilisé pour indiquer des sommes d'argent et des mesures. Bien que s'étant étendu, en raison du rayonnement d'Athènes, à d'autres cités grecques, avec de nombreuses variantes dans les alphabets dits « épichoriques » (ou locaux), il a été détrôné par le système alphabétique.
Numération alphabétique
Ce système utilise, outre les lettres courantes de l'alphabet grec, trois lettres archaïques: le digamma (tracé le plus souvent comme un stigma), le koppa (distinct du koppa littéral ancien) et le sampi (combinaison d'une ancienne lettre sémitique et du pi). Purement additive, cette numération ne nécessite pas l'utilisation du zéro, alors inconnu. Le calcul basé sur ces écritures étant impossible, les anciens Grecs utilisaient des jetons placés sur des abaques de bois ou de marbre, divisés en colonnes.
La numération alphabétique est plus récente que la numération acrophonique. Elle a été introduite à Athènes en même temps que l'adoption du modèle ionien de Milet, en −403. Elle est cependant bien plus ancienne car on en trouve déjà des traces à Milet vers −700. On la nomme aussi pour cette raison « numération milésienne » ; l'alphabet de Milet, devenu « classique » grâce à Athènes, n'utilisait pas les trois lettres supplémentaires mentionnées dans l'écriture des mots : leur maintien dans la numération est donc un archaïsme qui s'explique par la nécessité d'avoir à disposition trois fois neuf signes différents.
Liste des signes
| Chiffre grec | Valeur | Prononciation |
|---|---|---|
| αʹ | 1 | alpha |
| βʹ | 2 | bêta |
| γʹ | 3 | gamma |
| δʹ | 4 | delta |
| εʹ | 5 | epsilon |
| ϝʹ (digamma δίγαμμα)/ϛʹ (stigma στίγμα) | 6 | digamma/stigma |
| ζʹ | 7 | dzêta |
| ηʹ | 8 | êta |
| θʹ | 9 | thêta |
| ιʹ | 10 | iota |
| κʹ | 20 | kappa |
| λʹ | 30 | lambda |
| μʹ | 40 | mu |
| νʹ | 50 | nu |
| ξʹ | 60 | ksi |
| οʹ | 70 | omicron |
| πʹ | 80 | pi |
| ϟʹ (koppa κόππα) | 90 | koppa |
| ρʹ | 100 | rô |
| σʹ | 200 | sigma |
| τʹ | 300 | tau |
| υʹ | 400 | upsilon |
| φʹ | 500 | phi |
| χʹ | 600 | khi |
| ψʹ | 700 | psi |
| ωʹ | 800 | oméga |
| ϡʹ (sampi σάμπι) | 900 | sampi |
| ͵α | 1000 | |
| ͵β | 2000 | |
| ͵γ | 3000 | |
| ͵δ | 4000 | |
| ͵ε | 5000 | |
| ͵ϛ | 6000 | |
| ͵ζ | 7000 | |
| ͵η | 8000 | |
| ͵θ | 9000 |
Usages

| Valeur | Chiffres grecs | Lecture |
|---|---|---|
| 28 | κηʹ | kappa (20) + êta (8) + keréa (fin de nombre) |
| 666 | χξϛʹ | khi (600) + xi (60) + stigma (6) + keréa (fin de nombre) |
| 750 | ψνʹ | psi (700) + nu (50) + keréa (fin de nombre) |
| 1910 | ͵αϡιʹ | aristerí keréa (1000×) alpha (1) + sampi (900) + iota (10) + keréa |
| 4094 | ͵δϟδʹ | aristerí keréa (1000×) delta (4) + koppa (90) + delta (4) + keréa |
Dans l'Antiquité, l'usage était de surligner les lettres utilisées avec une valeur numérale afin de les distinguer du reste du texte. Avec l'arrivée de l'imprimerie, en raison de contraintes typographiques, le surlignement s'est mué en un signe unique placé à droite des lettres numériques et ressemblant à un accent aigu. Ce signe, nommé en grec κεραία keréa (corne) — κεραῖα keraĩa en grec ancien — ou parfois aussi désigné « apex[3] », est codé indépendamment par Unicode avec le point de code U+0374, « signe numéral grec » (équivalent au symbole prime avec le point de code U+02B9) pour keréa et avec le point de code U+0375, « signe numéral grec souscrit », pour aristerí keréa. De nombreux éditeurs ont confondu la κεραία avec l'accent aigu ou l'apostrophe, ce qui est sémantiquement incorrect.
Ainsi, le nombre 11 s’écrivait ιαʹ, avec la keréa. Pour les nombres supérieurs à 999, la keréa est remplacée par un autre caractère se plaçant à gauche, l’αριστερή κεραία (aristerí keréa) (corne placée à gauche) : ͵. Les deux keréas sont parfois employées conjointement.
Enfin, la lettre ϛ n'étant plus utilisée aujourd'hui, le chiffre 6 correspondant est noté par le digramme στ’ (ou plus souvent par la lettre ς avec laquelle ϛ se confond facilement, notamment dans les anciennes écritures onciales médiévales).
Pour signifier un nombre ordinal ou un dénominateur de fraction, on ajoutait en exposant la désinence du mot tel qu'il aurait été écrit en toutes lettres. Le dixième (Τὸ δέκατον) s'écrivait Τὸ ῑον.
Sur l'image ci-contre, la deuxième ligne se lit : ...τό ιβ αὐτοκράτορι, τό κε ὑπατίῳ, τό ιε ἐπιτειμήτῃ : « (à l'Empereur Domitien,...) chef suprême pour la 12e fois, consul pour la 25e fois, percepteur d'impôt pour la 15e fois... ». Dans notre transcription, les chiffres sont en gras. Sur les inscriptions lapidaires, on néglige très souvent les surlignages et les désinences. La kéréa est également absente, puisqu'elle est apparue à une date postérieure.
On employait les lettres de l'alphabet classique, sans lettres intercalaires, pour désigner les divisions d'un ouvrage. Ainsi, les 24 chants de l'Iliade ou de l'Odyssée étaient numérotés au moyen des 24 lettres de l'alphabet[4]. Cependant, le douzième livre, dit « Lambda » (Λ), de Métaphysique, d'Aristote, est donné avec la onzième lettre de l'alphabet ; il faut donc retenir une lettre intercalaire : en l'occurrence, le deuxième livre est numéroté avec un alpha minuscule (α).
Le système de numération alphabétique existe encore aujourd'hui en Grèce, à la manière des chiffres romains dans les pays de langues romanes. Il s'est transmis à certains alphabets dérivés du grec, notamment en copte, en arménien, dans la numération cyrillique utilisée en vieux slave, et mutatis mutandis en gotique. Parfois, les lettres sont aussi soulignées. En vieux slave, la barre de surlignement est devenue un tilde nommé titlo. Les dizaines suivent les unités jusqu'à dix-neuf inclus.
Numération « scientifique »
Outre la myriade (M') représentant dix mille (), on utilisait aussi la myriade de myriades (MM') pour représenter cent millions (). Diverses méthodes ont été proposées pour noter les grands nombres, notamment par Aristarque de Samos, Diophante d'Alexandrie et Apollonios de Perga. Ce dernier notait au moyen d'un symbole les diverses « classes » de myriades, dont chacune était un multiple de la précédente : en cinq ou six lettres, il était ainsi possible de noter des chiffres qui, dans notre système, seraient suivis de douzaines de zéros[5].
Dans l'Arénaire, Archimède proposa une méthode encore plus élaborée et proche de notre notation scientifique moderne pour nommer des nombres aussi grands que celui des grains de sable sur une plage, ou des grains de sable nécessaires pour remplir tout l'univers alors connu. Ce système de notation permet en fait d'atteindre des nombres aussi élevés que .
Le zéro
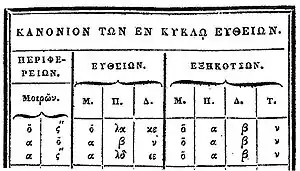
Les astronomes grecs étendirent le système alphabétique à un système sexagésimal en limitant chaque position à 50 + 9 et en créant un symbole spécial pour le zéro, qui était généralement utilisé isolément comme notre symbole moderne, plutôt que comme marqueur positionnel[6]. Cependant, contrairement à l'exemple reproduit ci-contre où aucune ambiguïté n'est possible, le symbole n'était généralement utilisé que pour la représentation de la partie fractionnaire des nombres (sous le nom de minutes (d'angle ou d'arc), secondes, etc.) et non pour la partie entière, sous peine d'être confondu avec le omicron de valeur 70. Le système qui consiste à diviser le cercle en 360 degrés, eux-mêmes divisés en minutes, secondes, tierces etc., et l'usage du zéro pour indiquer une valeur nulle furent probablement adaptés de la méthode babylonienne par Hipparque vers -140. Ces méthodes de notation furent ensuite utilisées notamment par Ptolémée (vers 140), Théon d'Alexandrie (vers 380), et la fille de Théon, Hypatie (morte en 415).
On suppose que le symbole utilisé pour zéro est issu de l'initiale de οὐδέν (rien), puisque le mot est parfois écrit en entier ou abrégé en οὐδ dans les tables et les textes astronomiques, surtout pour la partie entière des angles. Cependant cette hypothèse est contestée[7]. En effet, ces notations οὐδέν et οὐδ ne se rencontrent que dans des manuscrits relativement tardifs. Dans les papyri les plus anciens, il revêt la forme d'un très petit cercle surmonté d'une longue barre, symbole qui, selon Neugebauer, proviendrait d'une notation babylonienne en cunéiforme[8]. Il devint ensuite un omicron surmonté d'un macron moderne (ō), et finalement un simple omicron (ο).
Notes et références
- Le πῖ pĩ athénien ne se traçait pas comme le Π actuel.
- Le Η athénien notait encore /h/ et non /ɛː/.
- Marcel Cohen, 2005, p. 377.
- Marcel Cohen, 2005, p. 378.
- Georges Ifrah, p. 536-538.
- Voir, par exemple, HALMA, Almageste de Ptolémée, Eberhart, 1813 (cf. image) ou Les Tables faciles de Théon d'Alexandrie, Merlin, 1822 éditées et traduites également par l'abbé Halma
- Otto Neugebauer, The Exact Sciences in Antiquity (2e éd., Providence, RI: Brown University Press, 1957) 13-14.
- Les arguments de Neugebauer sont défendus par Raymond Mercier, Consideration of the Greek symbol "zero", en ligne sur Consideration of the Greek symbol 'zero'. On y constate cependant que la ressemblance avec le signe cunéiforme n'est pas évidente. La controverse reste donc ouverte.
Voir aussi
Bibliographie
- Marcel Cohen, « Histoire de l'écriture », dans M. Cohen et J. Peignot, Histoire et art de l'écriture, Paris, Robert Laffont, Coll. Bouquins, 2005. (ISBN 9782-221-102251)
- Georges Ifrah, Histoire universelle des chiffres, Paris, Robert Laffont, Coll. Bouquins, volume 1, chapitre 16. (ISBN 2-221-05779-1) (notice BnF no FRBNF35701745)
Articles connexes
Lien externe
- Portail de l’écriture
- Portail de la Grèce antique
- Portail des mathématiques
