Chiffres arabes
Les chiffres arabes sont, dans le langage courant, la graphie occidentale des dix chiffres (1, 2, 3, 4, 5, 6, 7, 8, 9, 0) et le système d'écriture décimale positionnelle qui les accompagne. Le principe est né en Inde et sa numération indienne, il est ensuite parvenu à l'Occident médiéval au contact des mathématiciens arabes via la civilisation andalouse. La graphie européenne est donc issue de la graphie du monde arabe médiéval occidental, d'où leur nom de chiffres arabes. Cette terminologie étant ambiguë, ils portent également d'autres noms permettant d'éviter les confusions, mais dont certains sont spécifiques à l'informatique : « chiffres ASCII », en référence à l'histoire ancienne de leur encodage, « chiffres européens », « chiffres latins », en référence au jeu de caractères auquel ils ont été associés, « chiffres occidentaux ».

Le nom « chiffres arabes » réfère parfois aussi aux chiffres utilisés dans l'écriture arabe. Aujourd'hui, le standard Unicode et la norme ISO/CEI 10646 permettent trois notations pour ces derniers[1]. Les différentes écritures de chiffres indiens et persans y sont également incluses.
Historique

La graphie des chiffres arabes pourrait s'inspirer d'une numération décimale non positionnelle Indienne datant du IIIe siècle av. J.-C., la numération Brahmi[2].
Un témoignage de leur utilisation en Inde est avéré en Syrie, au milieu du VIIe siècle, dans un commentaire de l'évêque Sévère Sebôkht sur les sciences grecques et les sciences orientales[3]. Ils sont repris par les mathématiques arabes et décrits dans un ouvrage du IXe siècle du mathématicien persan Al-Khwârizmî sur la numération décimale positionnelle[4].
Les chiffres arabes ont gagné l'Europe au Xe siècle par la péninsule Ibérique, alors sous domination omeyyade. Puis leur diffusion dans le reste de l'Occident s'est poursuivie par divers modes.
Certains mettent l'accent sur les travaux de Gerbert d'Aurillac (940–1003), le futur pape Sylvestre II, qui, selon la légende, aurait étudié à l'Université Al Quaraouiyine de Fès au Maroc[5], s'initiant aux sciences et techniques islamiques, étudiant les mathématiques et l'astronomie; plus probablement a-t-il simplement visité Cordoue et s'est-il appuyé sur les sources catalanes directement au contact du monde arabo-musulman. Ce dernier écrit un ouvrage sur la division, Libellus de numerorum divisione, Regulae de divisionibus, où Gerbert invente une méthode de division euclidienne qui sera rapportée par Bernelin (Bernélinus ou Bernelinus) de Paris, un de ses élèves ; et un traité concernant les multiplications, Libellus multiplicationum, qui prescrit l'antique multiplication par les doigts (calcul digital)[6].
D'autres attribuent un rôle majeur au mathématicien italien Leonardo Fibonacci (1175 — 1250), qui avait étudié auprès de professeurs musulmans à Béjaïa (dans l'actuelle Algérie), ramena à Pise en 1198 une partie de leur savoir et publia, en 1202, le Liber abaci (Le livre du calcul), un traité sur les calculs et la comptabilité fondée sur le calcul décimal.
Finalement, il est difficile d'établir lequel de ces deux érudits aura le plus promu la diffusion des mathématiques arabes en Occident, mais il n'en reste pas moins que Gerbert d’Aurillac et plus tard Fibonacci furent les auteurs des principaux ouvrages de vulgarisation des chiffres dits arabes.

Comme beaucoup de solutions qui nous paraissent simples, utiles et ingénieuses parce qu'elles nous sont familières, la diffusion des chiffres arabes s'est heurtée aux habitudes traditionnelles, et leur apprentissage a été progressif. À Florence (Italie), il fut d'abord interdit aux marchands de les employer dans les contrats et les documents officiels[7]. En 1299, ils sont partout interdits, y compris dans la comptabilité privée des banquiers et marchands florentins[8]. Tant que les opérations restent simples, l'abaque pour le calcul et les chiffres romains pour la représentation graphique suffisent. À partir de la Renaissance, avec le développement exponentiel du commerce, puis des sciences, en particulier de l'astronomie et de la balistique, la nécessité d'un système de calcul puissant et rapide s'impose : les chiffres indo-arabes écartent définitivement leurs prédécesseurs romains. Leur tracé définitif, normalisé, est attesté dès le XVe siècle.
Étymologie
Le mot chiffre vient de l'arabe صفر (ṣifr), signifiant « zéro » qui est calqué sur le sanskrit « sunya » désignant le vide et aussi le « zéro »[9]. Le zéro constituant l'innovation la plus importante du système de chiffres, il a fini par désigner l'ensemble des chiffres. « Zéro » dérive d'ailleurs du mot italien « zefiro », signifiant « vide », lui-même étant dérivé du même mot arabe صفر (ṣifr)[10].
Graphies d'origine commune
 Clavier téléphonique en Égypte : chaque touche est indiquée à la fois en chiffres arabes « occidentaux » et « orientaux ».
Clavier téléphonique en Égypte : chaque touche est indiquée à la fois en chiffres arabes « occidentaux » et « orientaux ». Présentation d'un numéro de téléphone avec la numération utilisée en Europe et la numération utilisée en Égypte.
Présentation d'un numéro de téléphone avec la numération utilisée en Europe et la numération utilisée en Égypte.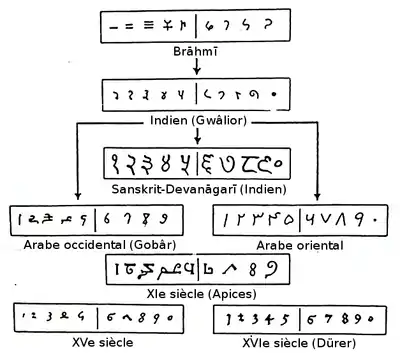
La graphie des chiffres arabes « occidentaux », dits « ghûbar »[11], diffère de leurs aînés arabes proprement dits et de leurs équivalents indiens.
Voici une comparaison rapide entre les tracés actuels des chiffres dits « arabes », utilisés notamment en Occident, par rapport aux chiffres que certains pays arabes utilisent aujourd'hui (chiffres hindî) et les chiffres tels que tracés dans plusieurs écritures indiennes.
| Tracé | Système d'écriture | Caractères | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Occidental/Maghreb/Andalous | Arabe/Latin | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Arabe | Arabe oriental (hors persan et ourdou) | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Persan | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | |
| Ourdou | |||||||||||
| Indien | Bengalais | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Devanagari | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | |
| Gujarati | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | |
| Gurmukhi | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | |
Les pays du Maghreb utilisent uniquement les tracés modernes, contrairement au pays du Machreq (ou Moyen-Orient) qui utilisent les deux. Ce type de tracé européen a été probablement inventé en Espagne, probablement dans al-Andalus.
Le développement des chiffres décimaux dans l'Europe jusqu'au XVIIIe siècle est montré dans l'illustration ci-dessous de Jean-Étienne Montucla, qui fut publiée 1758 dans son Histoire de la mathématique :

Variantes graphiques en écriture manuscrite
- Les informaticiens et les militaires représentent parfois le chiffre zéro, « 0 », en le traversant d'une barre oblique, pour éviter la confusion avec la lettre « O », ce qui le rapproche de la lettre scandinave « Ø ».
- Les francophones et les Européens en général écrivent très souvent le chiffre « 1 » muni d'une barre courte oblique descendant vers la gauche à partir du sommet, ainsi que muni d'une courte barre horizontale en bas du chiffre (« 1 »). Les anglophones et les francophones d'Amérique du Nord se contentent souvent d'une barre verticale (|). En informatique, la forme francophone (« 1 ») est la plus couramment utilisée, car elle permet d'éviter toute confusion avec la lettre I majuscule.
- Les francophones et les Européens en général écrivent souvent le chiffre « 7 » muni d'une traverse médiane (ressemblant plus ou moins à «
7») qui évite la confusion avec leur chiffre « 1 ». Ceci est très rare chez les anglophones et les francophones d'Amérique du Nord.
- La variante graphique ouverte de 4 est couramment utilisée en écriture manuscrite.
Notes et références
- Zghibi Rachid, « Le codage informatique de l'écriture arabe : d'ASMO 449 à Unicode et ISO/CEI 10646 », Document numérique, Lavoisier, vol. 6, , p. 155-182 (DOI 10.3166/dn.6.3-4.155-182, lire en ligne, consulté le )
- (en) J J O'Connor and E F Robertson, « Indian numerals », sur MacTutor History of Mathematics archive, (consulté le )
- Georges Ifrah, Histoire universelle des chiffres, Seghers,1981, p. 466.
- Georges Ifrah, Histoire universelle des chiffres, Seghers,1981, p. 493.
- « Histoire : Le pape Sylvestre II, lauréat d'Al Quaraouiyine à l’origine des croisades ? », sur Yabiladi.com (consulté le ).
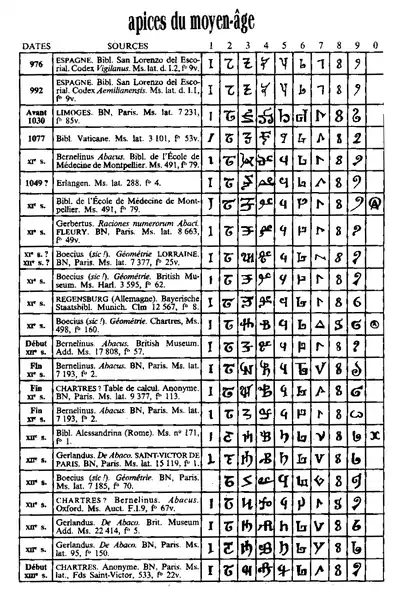
- Gerbert est aussi à l'origine d'un type particulier d'abaque, l’abaque de Gerbert où les jetons multiples sont remplacés par un jeton unique portant comme étiquette un chiffre dit « arabe » : les sept jetons de la colonne unité sont remplacés par un jeton portant le numéro 7, les trois jetons de la colonne dizaine par un jeton portant le chiffre 3, etc. Selon Jacques Halbronn (Mathématiques Divinatoires, Paris, La Grande Conjonction -Trédaniel, 1983), il conviendrait de rapprocher la graphie de ces chiffres de la cursive hébraïque, notamment les lettres Daleth, Tsadé, Samekh, Vav, Zayin pour le 2, le 3, le 0, le 1 et le 5 ; dont dérivent les cinq autres par l'adjonction d'un trait : 4, 9, 8, 7 et 6.
- . Sans doute parce qu'il est très facile de rajouter un zéro pour faire, par exemple, passer une somme de cent à mille (risque de fraude ou d'erreur qui existe encore aujourd'hui). D’où l’obligation, encore actuelle[réf. souhaitée], d’écrire une somme à la fois en chiffres et en toutes lettres dans les contrats.
- John D. Barrow, Pi in the sky.
- Cf. l'étymologie du mot dans TLFi
- (en) David Eugene Smith & Louis Charles Karpinski The Hindu-Arabic Numerals p. 58
- Chiffres anglés et arabisés à tort
Voir aussi
Articles connexes
- Numération indienne
- Numération arabe
- Al-Khwârizmî
- Système décimal
- Système de numération
- Nombres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Nombres dans le monde
- Nombres en français
- Système de numération indo-arabe
- Portail des mathématiques