Mathématiques en MP/Exercices/Intégrales dépendant d'un paramètre

Rappels de cours

Dans les trois théorèmes suivants, toutes les fonctions seront supposées (outre les hypothèses spécifiques à chacun) continues par morceaux, pour éviter de faire appel à la notion de mesurabilité, plus générale mais peu utile dans les cas concrets. $J$ désignera un intervalle réel et $f$ une application définie sur $J\times \left[a,b\right[$ et à valeurs dans $\mathbb {R}$ ou $\mathbb {C}$ ( $b$ peut être infini). On définit

F(x):=\int _{a}^{b}f(x,t)\,\mathrm {d} t

(pour les $x\in J$ pour lesquels cette intégrale converge).

Limite

Soit $x_{0}$ une extrémité (éventuellement infinie) de l'intervalle $J$ . Si :

$\forall t\in \left[a,b\right[\quad \lim _{x\to x_{0}}f(x,t)$ existe ;
$\forall (x,t)\in J\times \left[a,b\right[\quad |f(x,t)|\leq g(t)$ pour une certaine fonction $g$ intégrable sur $\left[a,b\right[$ ,

alors :

$F$ est bien définie sur $J$ et $\lim _{x\to x_{0}}F(x)=\int _{a}^{b}\lim _{x\to x_{0}}f(x,t)\,\mathrm {d} t$ .

Continuité

Si :

$\forall t\in \left[a,b\right[\quad x\mapsto f(x,t)$ est continue sur $J$ ;
$\forall (x,t)\in J\times \left[a,b\right[\quad |f(x,t)|\leq g(t)$ pour une certaine fonction $g$ intégrable sur $\left[a,b\right[$ ,

alors :

$F$ est bien définie et continue sur $J$ .

Classe C¹

Si $F$ est bien définie sur $J$ et si :

$\forall t\in \left[a,b\right[\quad x\mapsto f(x,t)$ est de classe C¹ sur $J$ ;
$\forall (x,t)\in J\times \left[a,b\right[\quad \left|{\frac {\partial f}{\partial x}}(x,t)\right|\leq g(t)$ pour une certaine fonction $g$ intégrable sur $\left[a,b\right[$ ,

alors :

$F$ est de classe C¹ sur $J$ et $\forall x\in J\quad F'(x)=\int _{a}^{b}{\frac {\partial f}{\partial x}}(x,t)\,\mathrm {d} t$ .

Exercice 2-1

On considère $g(x):=\int _{0}^{+\infty }f(x,t)\,\mathrm {d} t$ , pour $f:\mathbb {R} \times \left[0,+\infty \right[\to \mathbb {R} ,\,(x,t)\mapsto {\frac {x}{1+x^{2}t^{2}}}$ .

Montrer que $f$ est continue (sur $\mathbb {R} \times \left[0,+\infty \right[$ ) et que $g$ est bien définie sur $\mathbb {R}$ .
Pour tout $x\in \mathbb {R}$ , calculer $g(x)$ .
Pour tout $t\in \left]0,+\infty \right[$ , calculer $h(t):=\sup _{x\in \mathbb {R} }\left|f(x,t)\right|$ .
L'intégrale $\int _{0}^{+\infty }h(t)\,\mathrm {d} t$ est-elle convergente ?
Étudier de même $h_{\varepsilon ,M}(t):=\sup _{\varepsilon \leq |x|\leq M}\left|f(x,t)\right|$ , pour $0<\varepsilon \leq M$ .

Solution

$f(0,t)=0$ donc $g(0)=0$ .
$f$ est continue car c'est une fraction rationnelle (en deux variables) dont le dénominateur ne s'annule pas.
De plus, pour $x\in \mathbb {R} ^{*}$ fixé, $t\mapsto f(x,t)$ est intégrable en $+\infty$ car (par changement de variable $s=|x|t$ )
$\int _{0}^{+\infty }{\frac {|x|}{1+x^{2}t^{2}}}\,\mathrm {d} t=\int _{0}^{+\infty }{\frac {1}{1+s^{2}}}\,\mathrm {d} s={\frac {\pi }{2}}<+\infty$ .
Donc $g$ est bien définie sur $\mathbb {R}$ .
Par le même calcul, $g(x)={\begin{cases}{\frac {\pi }{2}}&{\text{si }}x>0,\\-{\frac {\pi }{2}}&{\text{si }}x<0,\\0&{\text{si }}x=0.\end{cases}}$
$h(t)=\sup _{x\in \mathbb {R} }{\frac {|x|}{1+x^{2}t^{2}}}={\frac {1}{t}}\sup _{s\geq 0}{\frac {s}{1+s^{2}}}={\frac {1}{2t}}$ .
Non ( $h$ $h$ n'est même intégrable ni en $0$ $0$ , ni en $+\infty$ $+\infty$ ) : d'après la question 3, ou simplement d'après la question 2.
Sinon, les théorèmes de continuité et d'interversion des limites pour une intégrale à paramètre s'appliqueraient, or :
- $g$ n'est pas continue en $0$ ;
- $\int _{0}^{+\infty }\lim _{x\to +\infty }{\frac {x}{1+x^{2}t^{2}}}\,\mathrm {d} t=\int _{0}^{+\infty }0\,\mathrm {d} t=0\neq {\frac {\pi }{2}}$ .
$h_{\varepsilon ,M}(t)=\sup _{\varepsilon \leq |x|\leq M}{\frac {|x|}{1+x^{2}t^{2}}}={\frac {1}{t}}\sup _{\varepsilon t\leq s\leq Mt}{\frac {s}{1+s^{2}}}={\begin{cases}{\frac {M}{1+M^{2}t^{2}}}&{\text{si }}t\leq 1/M\\{\frac {1}{2t}}&{\text{si }}1/M\leq t\leq 1/\varepsilon \\{\frac {\varepsilon }{1+\varepsilon ^{2}t^{2}}}&{\text{si }}t\geq 1/\varepsilon \end{cases}}$
donc $h_{\varepsilon ,M}$ est (continue et) intégrable en $0$ et en $+\infty$ . Ceci permettrait, si l'on n'avait pas déjà calculé $g$ , de démontrer que cette fonction est continue sur $\mathbb {R} ^{*}$ .

Sur le même thème : pour $x\in \mathbb {R}$ , on pose $f(x,t)={\frac {x\sin(xt)}{t}}$ et $\psi (x)=\int _{0}^{+\infty }f(x,t)\;\mathrm {d} t$ .

Montrer que $\psi$ est de classe C^∞ sur $\mathbb {R} ^{*}$ mais que $\psi '(x)\neq \int _{0}^{+\infty }{\frac {\partial f}{\partial x}}(x,t)\;\mathrm {d} t$ .

Solution

Par changement de variable $y=xt$ , on obtient : $\psi (x)=|x|\psi (1)$ donc $\psi$ est C^∞ sur $\mathbb {R} ^{*}$ .

Mais pour tout $x\neq 0$ , l'intégrale de $0$ à $+\infty$ de $t\mapsto {\frac {\partial f}{\partial x}}(x,t)={\frac {\sin(xt)}{t}}+x\cos(xt)$ diverge, comme somme d'une intégrale (semi-)convergente et d'une intégrale divergente.

Exercice 2-2

On pose $I_{n}:=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{\left(1+t^{2}\right)^{n}}}$ pour tout $n\in \mathbb {N} ^{*}$ et $g(x):=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{x+t^{2}}}$ pour tout $x>0$ .

À l'aide du théorème de dérivation pour les intégrales à paramètre, montrer que $g$ est de classe C^∞ sur $\mathbb {R} _{+}^{*}$ et donner une relation entre la suite $\left(I_{n}\right)$ et la suite des dérivées successives de $g$ au point $1$ .
Calculer directement $g$ à partir de sa définition, et en déduire l'expression de ses dérivées.
En déduire $I_{n}$ .

Solution

Pour tout $k\in \mathbb {N}$ , $(x,t)\mapsto {\frac {\partial ^{k}}{\partial x^{k}}}\left({\frac {1}{x+t^{2}}}\right)={\frac {(-1)^{k}k!}{\left(x+t^{2}\right)^{k+1}}}$ est continue sur $\mathbb {R} _{+}^{*}\times \mathbb {R} _{+}$ mais
$t\mapsto \sup _{x>0}{\frac {1}{\left(x+t^{2}\right)^{k+1}}}={\frac {1}{t^{2k+2}}}$ n'est pas intégrable (en 0) donc
les hypothèses ne sont pas satisaites pour appliquer directement le théorème de dérivation pour $x\in \left]0,+\infty \right[$ .
Appliquons-le alors (pour s'écarter de $x=0$ en lequel ce sup non intégrable est atteint) pour $x\in \left]\varepsilon ,+\infty \right[$ (avec $\varepsilon >0$ ) :
$t\mapsto \sup _{x>\varepsilon }{\frac {1}{\left(x+t^{2}\right)^{k+1}}}={\frac {1}{\left(\varepsilon +t^{2}\right)^{k+1}}}$ est (continue et) intégrable sur $\left[0,+\infty \right[$ , ce qui prouve (par récurrence) que
$\forall k\in \mathbb {N} \quad \forall x>\varepsilon \quad g^{(k)}(x)=\int _{0}^{+\infty }{\frac {(-1)^{k}k!}{\left(x+t^{2}\right)^{k+1}}}\,\mathrm {d} t$ .
Ceci étant vrai pour tout $x\in \cup _{\varepsilon >0}\left]\varepsilon ,+\infty \right[=\left]0,+\infty \right[$ , $g$ est bien de classe C^∞ sur $\mathbb {R} _{+}^{*}$ .
En particulier, $g^{(k)}(1)=(-1)^{k}k!\,I_{k+1}$ .
Par changement de variable $t=s{\sqrt {x}}$ ,
$g(x)={\frac {1}{\sqrt {x}}}\int _{0}^{+\infty }{\frac {\mathrm {d} s}{1+s^{2}}}=x^{-1/2}{\frac {\pi }{2}}$ donc
$\forall k\in \mathbb {N} \quad g^{(k)}(x)=x^{-(2k+1)/2}\pi \,{\frac {(-1)^{k}\cdot 1\cdot 3\cdots (2k-1)}{2^{k+1}}}=x^{-(2k+1)/2}\pi \,{\frac {(-1)^{k}(2k)!}{2^{2k+1}k!}}$ .
$\forall k\in \mathbb {N} \quad (-1)^{k}k!\,I_{k+1}=g^{(k)}(1)=(-1)^{k}\pi \,{\frac {(2k)!}{2^{2k+1}k!}}$ donc (en remplaçant $k$ par $n-1$ )
$\forall n\in \mathbb {N} ^{*}\quad I_{n}=\pi \,{\frac {(2n-2)!}{2^{2n-1}\left((n-1)!\right)^{2}}}$ .

Variante : pour $n\in \mathbb {N} ^{*}$ et $x\in \left]0,+\infty \right[$ , on pose

I_{n}(x)=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{(t^{2}+x^{2})^{n}}}

.

Montrer que $I_{n}(x)$ est bien définie et dérivable sur $\left]0,+\infty \right[$ . Calculer sa dérivée.
En déduire la valeur de $\int _{0}^{+\infty }{\frac {\mathrm {d} t}{(t^{2}+1)^{3}}}$ .

Solution

Cf. exercice 2-8 ci-dessus. Pour $t\in \mathbb {R} _{+}$ et $x\in \mathbb {R} _{+}^{*}$ , notons $f(t,x)={\frac {1}{(t^{2}+x^{2})^{n}}}$ . L'intégrale $I_{n}(1)$ converge et pour tout $t\in \mathbb {R} _{+}$ , $x\mapsto f(t,x)$ est de classe C¹ sur $\mathbb {R} _{+}^{*}$ . De plus, pour tout $x>\varepsilon >0$ et tout $t\in \mathbb {R} _{+}$ , $\left|{\frac {\partial f}{\partial x}}(t,x)\right|=\left|-{\frac {2nx}{(t^{2}+x^{2})^{n+1}}}\right|\leq {\frac {2n}{(t^{2}+x^{2})^{n+{\frac {1}{2}}}}}\leq {\frac {2n}{(t^{2}+\varepsilon ^{2})^{n+{\frac {1}{2}}}}}$ , or $\int _{0}^{+\infty }{\frac {\mathrm {d} t}{(t^{2}+x^{2})^{n+{\frac {1}{2}}}}}<+\infty$ . Par conséquent, $I_{n}$ est bien définie et C¹ sur la réunion des $\left]\varepsilon ,+\infty \right[\subset \mathbb {R} _{+}^{*}$ c'est-à-dire sur $\mathbb {R} _{+}^{*}$ , et sur cet ensemble on a : $I_{n}'(x)=-2nx\int _{0}^{+\infty }{\frac {\mathrm {d} t}{(t^{2}+x^{2})^{n+1}}}=-2nxI_{n+1}(x)$ . (Le « garde-fou » $\varepsilon >0$ était indispensable car sans même calculer la fonction $t\mapsto \sup _{x>0}{\frac {x}{(t^{2}+x^{2})^{n+1}}}$ , on peut affirmer que son intégrale de $0$ à $+\infty$ diverge, sinon on en déduirait que $I_{n}$ est de classe C¹ sur $\mathbb {R} _{+}$ , alors qu'en réalité elle n'est même pas définie en $0$ .)
Soit $x>0$ . Par changement de variable $t=xs$ , $I_{1}(x)={\frac {1}{x}}\int _{0}^{+\infty }{\frac {\mathrm {d} s}{s^{2}+1}}={\frac {\pi }{2x}}$ . On en déduit que $\forall x>0\quad I_{2}(x)=-{\frac {1}{2x}}I'_{1}(x)={\frac {\pi }{2x^{3}}}$ , puis $\forall x>0\quad I_{3}(x)=-{\frac {1}{4x}}I'_{2}(x)={\frac {3\pi }{16x^{5}}}$ .

$I_{n}(x)$ peut aussi se déduire de $I_{n}(1)$ par changement de variable, et $I_{n}(1)$ peut se calculer par récurrence à l'aide d'une IPP (cf. Intégration de Riemann/Exercices/Intégrales impropres#Exercice 5-7 question 1). Il s'agit en fait d'une intégrale de Wallis.

Exercice 2-3

On sait bien que l'intégrale de Dirichlet $I:=\int _{0}^{+\infty }{\frac {\sin t}{t}}\,\mathrm {d} t$ converge, mais non absolument.

Le but de cet exercice est de retrouver sa valeur en appliquant le théorème de dérivation d'une intégrale à paramètre à la fonction

g(x):=\int _{0}^{+\infty }{\frac {\sin t}{t}}\,\operatorname {e} ^{-xt}\,\mathrm {d} t

.

Montrer que $g$ est de classe C¹ sur $\mathbb {R} _{+}^{*}$ et calculer $g'(x)$ , $\lim _{+\infty }g$ , puis $g(x)$ .
Montrer que $\lim _{0^{+}}g=I$ $\lim _{0^{+}}g=I$ . Pour cela, on est certain de ne pas pouvoir appliquer le théorème d'interversion de $\lim _{x\to 0^{+}}$ $\lim _{x\to 0^{+}}$ avec $\int _{0}^{+\infty }$ $\int _{0}^{+\infty }$ , car si pour tout $x>0$ $x>0$ (ou au moins tout $x>0$ $x>0$ proche de $0$ $0$ ) $\left|{\frac {\sin t}{t}}\,\operatorname {e} ^{-xt}\right|\leq \varphi (t)$ $\left|{\frac {\sin t}{t}}\,\operatorname {e} ^{-xt}\right|\leq \varphi (t)$ , alors (par passage à la limite) $\varphi (t)\geq \left|{\frac {\sin t}{t}}\right|$ $\varphi (t)\geq \left|{\frac {\sin t}{t}}\right|$ , or $\left|{\frac {\sin t}{t}}\right|$ $\left|{\frac {\sin t}{t}}\right|$ n'est pas intégrable en $+\infty$ $+\infty$ . Par contre, on pourra facilement intervertir $\lim _{x\to 0^{+}}$ $\lim _{x\to 0^{+}}$ avec $\int _{0}^{A}$ $\int _{0}^{A}$ pour $A$ $A$ fixé (la question de l'intégrabilité en $+\infty$ $+\infty$ ne se posant plus). La méthode préconisée ici est de montrer que pour tout $A>0$ $A>0$ :
- $\forall x\geq 0\quad \left|\int _{A}^{+\infty }\sin t\,{\frac {\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t\right|\leq {\frac {2}{A}}$ ;
- $\lim _{x\to 0^{+}}\int _{0}^{A}{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\,\mathrm {d} t=0$ .
Conclure.

Solution

$(x,t)\mapsto {\frac {\sin t}{t}}\operatorname {e} ^{-xt}$ $(x,t)\mapsto {\frac {\sin t}{t}}\operatorname {e} ^{-xt}$ est de classe C^∞ sur $\left(\mathbb {R} _{+}^{*}\right)^{2}$ $\left(\mathbb {R} _{+}^{*}\right)^{2}$ ainsi, donc, que sa dérivée partielle par rapport à $x$ $x$ , $(x,t)\mapsto -\sin t\operatorname {e} ^{-xt}$ $(x,t)\mapsto -\sin t\operatorname {e} ^{-xt}$ .
De plus, pour tout $\varepsilon >0$ $\varepsilon >0$ , ces deux fonctions sont majorées en valeur absolue sur $\left]\varepsilon ,+\infty \right[\times \mathbb {R} _{+}^{*}$ $\left]\varepsilon ,+\infty \right[\times \mathbb {R} _{+}^{*}$ par $\operatorname {e} ^{-\varepsilon t}$ $\operatorname {e} ^{-\varepsilon t}$ , qui est intégrable sur $\mathbb {R} _{+}$ $\mathbb{R} _{+}$ .
Par conséquent, $g$ $g$ est (au moins) de classe C¹ sur $\mathbb {R} _{+}^{*}$ $\mathbb {R} _{+}^{*}$ et
- $\forall x>0\quad g'(x)=-\int _{0}^{+\infty }\sin t\operatorname {e} ^{-xt}\,\mathrm {d} t=-{\frac {1}{1+x^{2}}}$ $\forall x>0\quad g'(x)=-\int _{0}^{+\infty }\sin t\operatorname {e} ^{-xt}\,\mathrm {d} t=-{\frac {1}{1+x^{2}}}$ , par l'un ou l'autre des deux calculs suivants :
  - double intégration par parties : $g'(x)={\frac {1}{x}}{\cancel {\left[\sin t\operatorname {e} ^{-xt}\right]_{0}^{+\infty }}}-{\frac {1}{x}}\int _{0}^{+\infty }\cos t\operatorname {e} ^{-xt}\,\mathrm {d} t={\frac {1}{x^{2}}}\left[\cos t\operatorname {e} ^{-xt}\right]_{0}^{+\infty }-{\frac {g'(x)}{x^{2}}}$
  - simple intégration d'une exponentielle complexe : $g'(x)=\operatorname {Im} \left(\int _{0}^{+\infty }\operatorname {e} ^{-\left(x+\mathrm {i} \right)t}\,\mathrm {d} t\right)=\operatorname {Im} \left(\left[{\frac {\operatorname {e} ^{-\left(x+\mathrm {i} \right)t}}{-x-\mathrm {i} }}\right]_{0}^{+\infty }\right)=\operatorname {Im} \left({\frac {1}{x+\mathrm {i} }}\right)=\operatorname {Im} \left({\frac {x-\mathrm {i} }{x^{2}+1}}\right)$ ;
- $\lim _{+\infty }g=\int _{0}^{+\infty }\lim _{x\to +\infty }{\frac {\sin t}{t}}\operatorname {e} ^{-xt}\,\mathrm {d} t=0$ , d'où :
- $\forall x>0\quad g(x)={\frac {\pi }{2}}-\arctan x$ .
$\left|g(x)-I\right|\leq \left|\int _{A}^{+\infty }{\frac {\sin t}{t}}\,\operatorname {e} ^{-xt}\,\mathrm {d} t\right|+\left|\int _{A}^{+\infty }{\frac {\sin t}{t}}\,\operatorname {e} ^{-0t}\,\mathrm {d} t\right|+\left|\int _{0}^{A}{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\,\mathrm {d} t\right|$ $\left|g(x)-I\right|\leq \left|\int _{A}^{+\infty }{\frac {\sin t}{t}}\,\operatorname {e} ^{-xt}\,\mathrm {d} t\right|+\left|\int _{A}^{+\infty }{\frac {\sin t}{t}}\,\operatorname {e} ^{-0t}\,\mathrm {d} t\right|+\left|\int _{0}^{A}{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\,\mathrm {d} t\right|$ .
Pour prouver que $\lim _{0^{+}}g=I$ $\lim _{0^{+}}g=I$ , il suffit donc, pour tout $\varepsilon >0$ $\varepsilon >0$ , de montrer qu'il existe $A>0$ $A>0$ (indépendant de $x>0$ $x>0$ ) tel que les deux premiers des trois termes de cette somme soient majorés chacun par $\varepsilon /3$ $\varepsilon /3$ , puis de montrer qu'une fois fixé un tel $A$ $A$ , il existe $\delta >0$ $\delta >0$ tel que pour $x\in \left]0,\delta \right[$ $x\in \left]0,\delta \right[$ , le troisième terme soit également majoré par $\varepsilon /3$ $\varepsilon /3$ .
- Deux premiers termes :
  - par simple intégration d'une fonction à valeurs complexes :
    pour tout $x\geq 0$ , $\left|\int _{A}^{+\infty }\sin t\,{\frac {\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t\right|=\left|\operatorname {Im} \left(\int _{A}^{+\infty }{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{t}}\,\mathrm {d} t\right)\right|\leq \left|\int _{A}^{+\infty }{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{t}}\,\mathrm {d} t\right|$ et
    $\int _{A}^{+\infty }{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{t}}\,\mathrm {d} t=\left[{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{-x+\mathrm {i} }}{\frac {1}{t}}\right]_{A}^{+\infty }+\int _{A}^{+\infty }{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{-x+\mathrm {i} }}{\frac {\mathrm {d} t}{t^{2}}}=-{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)A}}{-x+\mathrm {i} }}{\frac {1}{A}}+\int _{A}^{+\infty }{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{-x+\mathrm {i} }}{\frac {\mathrm {d} t}{t^{2}}}$ , d'où
    $\left|\int _{A}^{+\infty }\sin t\,{\frac {\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t\right|\leq \left|{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)A}}{-x+\mathrm {i} }}{\frac {1}{A}}\right|+\int _{A}^{+\infty }\left|{\frac {\operatorname {e} ^{\left(-x+\mathrm {i} \right)t}}{-x+\mathrm {i} }}\right|{\frac {\mathrm {d} t}{t^{2}}}={\frac {\operatorname {e} ^{-xA}}{\sqrt {x^{2}+1}}}{\frac {1}{A}}+\int _{A}^{+\infty }{\frac {\operatorname {e} ^{-xt}}{\sqrt {x^{2}+1}}}{\frac {\mathrm {d} t}{t^{2}}}\leq {\frac {1}{A}}+\int _{A}^{+\infty }{\frac {\mathrm {d} t}{t^{2}}}={\frac {2}{A}}$ .
  - ou si l'on préfère vraiment, par une double intégration par parties :
    $\int _{A}^{+\infty }{\frac {\sin t\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t=\left[-\cos t{\frac {\operatorname {e} ^{-xt}}{t}}\right]_{A}^{+\infty }-x\int _{A}^{+\infty }{\frac {\cos t\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t-\int _{A}^{+\infty }\cos t{\frac {\operatorname {e} ^{-xt}}{t^{2}}}\,\mathrm {d} t$ et
    $\int _{A}^{+\infty }{\frac {\cos t\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t=\left[\sin t{\frac {\operatorname {e} ^{-xt}}{t}}\right]_{A}^{+\infty }+x\int _{A}^{+\infty }{\frac {\sin t\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t+\int _{A}^{+\infty }\sin t{\frac {\operatorname {e} ^{-xt}}{t^{2}}}\,\mathrm {d} t$ , donc
    $\left(1+x^{2}\right)\int _{A}^{+\infty }{\frac {\sin t\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t=(\cos A+x\sin A){\frac {\operatorname {e} ^{-xA}}{A}}-\int _{A}^{+\infty }(\cos t+x\sin t){\frac {\operatorname {e} ^{-xt}}{t^{2}}}\,\mathrm {d} t$ , si bien que
    $\left|\int _{A}^{+\infty }\sin t\,{\frac {\operatorname {e} ^{-xt}}{t}}\,\mathrm {d} t\right|\leq {\frac {1}{1+x^{2}}}\left({\sqrt {1+x^{2}}}{\frac {\operatorname {e} ^{-xA}}{A}}+\int _{A}^{+\infty }{\sqrt {1+x^{2}}}{\frac {\operatorname {e} ^{-xt}}{t^{2}}}\,\mathrm {d} t\right)$ ,
    et l'on conclut comme par la première méthode.
- Troisième terme (pour $A$ fixé) : $\left|{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\right|\leq 1$ , intégrable sur $\left]0,A\right[$ , donc
  $\lim _{x\to 0^{+}}\int _{0}^{A}{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\,\mathrm {d} t=\int _{0}^{A}\lim _{x\to 0^{+}}{\frac {\sin t}{t}}\,\left(\operatorname {e} ^{-xt}-1\right)\,\mathrm {d} t=\int _{0}^{A}0\,\mathrm {d} t=0$ .
$I=\lim _{x\to 0^{+}}\left({\frac {\pi }{2}}-\arctan x\right)={\frac {\pi }{2}}$ .

Exercice 2-4

On considère la fonction Gamma d'Euler, définie par

\Gamma (x):=\int _{0}^{+\infty }t^{x-1}\operatorname {e} ^{-t}\,\mathrm {d} t

.

On sait déjà (cf. devoir sur la fonction Gamma et la formule de Stirling) que :

son domaine de définition est $\mathbb {R} _{+}^{*}$ ;
$\Gamma (x+1)=x\,\Gamma (x)$ (pour $x>0$ ) ;
$\Gamma (n+1)=n!$ (pour $n\in \mathbb {N}$ ).

Montrer que $\Gamma$ est de classe C^∞ et donner l'expression de $\Gamma ^{(k)}$ pour tout $k\in \mathbb {N}$ .
Montrer que $\Gamma ''>0$ et en déduire que $\Gamma '$ s'annule au plus une fois.
Montrer que $\Gamma '$ s'annule entre 1 et 2.
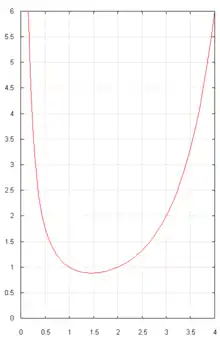
Déterminer $\lim _{x\to 0^{+}}x\,\Gamma (x)$ , $\lim _{0^{+}}\Gamma$ , $\lim _{+\infty }\Gamma$ , $\lim _{x\to +\infty }\Gamma (x)/x$ et donner l'allure du graphe de $\Gamma$ .
Calculer $\Gamma (1/2)$ , connaissant la valeur de l'intégrale de Gauss ( $\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\,\mathrm {d} s={\frac {\sqrt {\pi }}{2}}$ ).

Solution

Pour tout $k\in \mathbb {N}$ , la fonction $(x,t)\mapsto {\frac {\partial ^{k}}{\partial x^{k}}}\left(t^{x-1}\operatorname {e} ^{-t}\right)=(\ln t)^{k}\,t^{x-1}\,\operatorname {e} ^{-t}$ est continue sur $\mathbb {R} \times \mathbb {R} _{+}^{*}$ . Pour $0<\varepsilon <M$ , la fonction $t\mapsto \sup _{\varepsilon <x<M}|\ln t|^{k}\,t^{x-1}\,\operatorname {e} ^{-t}={\begin{cases}|\ln t|^{k}\,t^{\varepsilon -1}\,\operatorname {e} ^{-t}&{\text{si }}t\leq 1\\0^{k}\,\operatorname {e} ^{-1}&{\text{si }}t=1\\|\ln t|^{k}\,t^{M-1}\,\operatorname {e} ^{-t}&{\text{si }}t\geq 1\\\end{cases}}$ est (continue par morceaux et) intégrable sur $\left]0,+\infty \right[$ donc (par récurrence) $\Gamma$ est au moins de classe C^k sur $\cup _{0<\varepsilon <M}\left]\varepsilon ,M\right[=\left]0,+\infty \right[$ et $\Gamma ^{(k)}(x)=\int _{0}^{+\infty }(\ln t)^{k}\,t^{x-1}\,\operatorname {e} ^{-t}\,\mathrm {d} t$ .
$\Gamma ''(x)=\int _{0}^{+\infty }(\ln t)^{2}\,t^{x-1}\,\operatorname {e} ^{-t}\,\mathrm {d} t>0$ donc $\Gamma '$ est strictement croissante. Par conséquent, elle s'annule au plus une fois.
$\Gamma (1)=0!=1$ et $\Gamma (2)=1!=1$ donc (théorème de Rolle) $\Gamma '$ s'annule entre 1 et 2.
$\lim _{x\to 0^{+}}x\,\Gamma (x)=\lim _{x\to 0^{+}}\Gamma (x+1)=\Gamma (1)=1$ donc $\lim _{0^{+}}\Gamma =+\infty$ .
Puisque $\Gamma$ est strictement croissante sur $\left[2,+\infty \right[$ , sa convexité implique que $\lim _{+\infty }\Gamma =+\infty$ (ou plus élémentairement : $\lim _{+\infty }\Gamma =\lim n!=+\infty$ , ou même : $\Gamma (x)\geq 2^{x}\int _{2}^{+\infty }t^{-1}\operatorname {e} ^{-t}\,\mathrm {d} t$ ), donc $\lim _{x\to +\infty }{\frac {\Gamma (x)}{x}}=\lim _{y\to +\infty }{\frac {\Gamma (y+1)}{y+1}}=\lim _{y\to +\infty }{\frac {y}{y+1}}\,\Gamma (y)=1\times \lim _{+\infty }\Gamma =+\infty$ . On en déduit le graphe ci-contre.
$\Gamma (1/2)=\int _{0}^{+\infty }\operatorname {e} ^{-t}\,{\frac {\mathrm {d} t}{\sqrt {t}}}=\int _{0}^{+\infty }\operatorname {e} ^{-s^{2}}\,2\mathrm {d} s={\sqrt {\pi }}$ .

Exercice 2-5

On définit la fonction bêta par : $\mathrm {B} (x,y):=\int _{0}^{1}t^{x-1}(1-t)^{y-1}\,\mathrm {d} t$ .

Montrer que cette intégrale converge si et seulement si les deux réels $x$ et $y$ sont strictement positifs.
Montrer que $\mathrm {B} (x,y)={\frac {\Gamma (x)\,\Gamma (y)}{\Gamma (x+y)}}$ (la définition de $\Gamma$ est rappelée dans l'exercice précédent). Pour cette question, on admettra le théorème de Fubini car explicitement hors programme en classe de MP.
En déduire une expression simple de $\mathrm {B} (x,n+1)$ si $n\in \mathbb {N}$ .
Démontrer que $\forall x>0\quad \Gamma (x)=\lim _{n\to +\infty }\int _{0}^{n}t^{x-1}\left(1-{\frac {t}{n}}\right)^{n}\,\mathrm {d} t=\lim _{n\to +\infty }{\frac {n!\;n^{x}}{x\;(x+1)\cdots (x+n)}}={\frac {1}{x}}\lim _{n\to +\infty }\prod _{k=1}^{n}{\frac {\left(1+{\frac {1}{k}}\right)^{x}}{1+{\frac {x}{k}}}}$ .
En déduire que la fonction ${\frac {1}{\Gamma }}$ se prolonge en une fonction holomorphe sur $\mathbb {C}$ , dont les seuls zéros sont les entiers négatifs ou nuls.

Solution

L'intégrande est continu sur $\left]0,1\right[$ et équivalent à $t^{x-1}$ en 0 et à $(1-t)^{y-1}$ en 1, donc l'intégrale converge si et seulement si $x,y>0$ .
$\Gamma (x)\,\Gamma (y)=\int _{0}^{+\infty }s^{x-1}\operatorname {e} ^{-s}\mathrm {d} s\int _{0}^{+\infty }t^{y-1}\operatorname {e} ^{-t}\mathrm {d} t$ .
Soit le changement de variables $s=uv,~t=u\left(1-v\right)$ , dont le jacobien vaut $u$ . Alors, par le théorème de Fubini,
$\Gamma (x)\,\Gamma (y)=\int _{0}^{+\infty }u^{x+y-1}\operatorname {e} ^{-u}\,\mathrm {d} u\int _{0}^{1}v^{x-1}(1-v)^{y-1}\,\mathrm {d} v=\Gamma (x+y)\,\mathrm {B} (x,y)$ .
$\mathrm {B} (x,n+1)={\frac {\Gamma (x)\,\Gamma (n+1)}{\Gamma (x+n+1)}}={\frac {n!}{x\;(x+1)\cdots (x+n)}}$ .
Pour $x>0$ fixé, les fonctions $f_{n}:t\mapsto {\begin{cases}t^{x-1}\left(1-{\frac {t}{n}}\right)^{n}&{\text{si }}0<t\leq n\\0&{\text{si }}t\geq n\end{cases}}$ sont continues, positives et majorées par leur limite simple, la fonction $t\mapsto t^{x-1}\operatorname {e} ^{-t}$ , intégrable sur $\mathbb {R} _{+}$ . Ceci justifie la première égalité. La seconde se déduit de la question précédente par changement de variable : $\int _{0}^{n}t^{x-1}\left(1-{\frac {t}{n}}\right)^{n}\,\mathrm {d} t=n^{x}\int _{0}^{1}s^{x-1}\left(1-s\right)^{n}\,\mathrm {d} s=n^{x}\,\mathrm {B} (x,n+1)$ . La troisième est immédiate.
Le produit infini ${\frac {1}{\Gamma (z)}}:=z\prod _{k\in \mathbb {N} ^{*}}{\frac {1+{\frac {z}{k}}}{\left(1+{\frac {1}{k}}\right)^{z}}}$ converge uniformément sur tout disque $D(0,R)$ car pour tout $z$ dans ce disque, on a $\left|\operatorname {Log} \left(1+{\frac {z}{k}}\right)-{\frac {z}{k}}\right|\leq {\frac {R^{2}}{k^{2}}}$ dès que $k\geq 2R$ (où $\mathrm {Log}$ désigne le logarithme complexe) et de même, $\left|z\operatorname {Log} \left(1+{\frac {1}{k}}\right)-{\frac {z}{k}}\right|\leq {\frac {R}{k^{2}}}$ dès que $k\geq 2$ , donc $\sum _{k\geq \max(2R,2)}\left|\operatorname {Log} \left(1+{\frac {z}{k}}\right)-z\operatorname {Log} \left(1+{\frac {1}{k}}\right)\right|\leq (R^{2}+R)\sum _{k\geq 2}{\frac {1}{k^{2}}}<\infty$

Exercice 2-6

On pose $f\left(x,t\right)={\frac {\ln \left(x^{2}+t^{2}\right)}{1+t^{2}}}$ puis $I\left(x\right)=\int _{0}^{+\infty }f\left(x,t\right)\,\mathrm {d} t$ .

Montrer que l'application $I$ est définie et continue sur $\mathbb {R}$ .
Montrer qu'elle est de classe C¹ sur $\mathbb {R} ^{*}$ .
Calculer $I'\left(x\right)$ .
À l'aide du changement de variable $s={\frac {1}{t}}$ , montrer que $I\left(0\right)=0$ .
En déduire une expression de $I\left(x\right)$ .

Solution

Pour tout $M>0$ , $f$ est continue sur $\left]-M,M\right[\times \mathbb {R} _{+}^{*}$ et $\forall \left(x,t\right)\in \left]-M,M\right[\times \mathbb {R} _{+}^{*}\quad \left|f\left(x,t\right)\right|\leq g\left(t\right):={\frac {\max \left(\left|\ln \left(t^{2}\right)\right|,\left|\ln \left(M^{2}+t^{2}\right)\right|\right)}{1+t^{2}}}$ .
La fonction positive $g$ est intégrable de $0$ à $+\infty$ car elle est continue sur $\mathbb {R} _{+}^{*}$ et $g(t)\sim _{t\to 0^{+}}2\left|\ln t\right|$ , intégrable en $0^{+}$ et $g(t)\sim _{t\to +\infty }{\frac {2\ln t}{t^{2}}}=o\left({\frac {1}{t^{3/2}}}\right)$ , intégrable en $+\infty$ .
Donc $I$ est définie et continue sur $\left]-M,M\right[$ , et ce pour tout $M>0$ . Par conséquent, elle est définie et continue sur $\cup _{M>0}\left]-M,M\right[=\mathbb {R}$ .
$I$ est paire donc il suffit de montrer qu'elle est de classe C¹ sur $\mathbb {R} _{+}^{*}$ .
La fonction $x\mapsto {\frac {\partial f\left(x,t\right)}{\partial x}}={\frac {2x}{\left(x^{2}+t^{2}\right)\left(1+t^{2}\right)}}$ est continue pour tout $t>0$ mais $\sup _{x>0}{\frac {2x}{\left(x^{2}+t^{2}\right)\left(1+t^{2}\right)}}$ est atteint pour $x=t$ et vaut ${\frac {1}{t\left(1+t^{2}\right)}}$ , non intégrable en $0$ .
Il faut donc fixer provisoirement pour $x$ un « garde-fou » $\varepsilon >0$ . En calculant, pour $t>0$ fixé, $h\left(t\right):=\sup _{x>\varepsilon }{\frac {2x}{\left(x^{2}+t^{2}\right)\left(1+t^{2}\right)}}$ , on trouve :
$\forall \left(x,t\right)\in \left]\varepsilon ,+\infty \right[\times \mathbb {R} _{+}^{*}\quad \left|{\frac {\partial f\left(x,t\right)}{\partial x}}\right|\leq h\left(t\right)={\begin{cases}{\frac {1}{t\left(1+t^{2}\right)}}&{\text{si }}t\geq \varepsilon \\{\frac {2\varepsilon }{\left(\varepsilon ^{2}+t^{2}\right)\left(1+t^{2}\right)}}&{\text{si }}t\leq \varepsilon .\end{cases}}$
La fonction positive $h$ est intégrable de $0$ à $+\infty$ car elle est continue sur $\mathbb {R} _{+}$ et $h(t)\sim _{t\to +\infty }{\frac {1}{t^{3}}}$ , intégrable en $+\infty$ .
Donc $I$ est de classe C¹ sur $\left]\varepsilon ,+\infty \right[$ avec $\forall x>\varepsilon \quad I'\left(x\right)=\int _{0}^{+\infty }{\frac {\partial f\left(x,t\right)}{\partial x}}\,\mathrm {d} t$ , et ce pour tout $\varepsilon >0$ . Par conséquent, elle est bien de classe C¹ sur $\cup _{\varepsilon >0}\left]\varepsilon ,+\infty \right[=\mathbb {R} _{+}^{*}$ .
Soit $x\in \mathbb {R} ^{*}$ , différent de $\pm 1$ (on en aura besoin au cours du calcul).
${\begin{aligned}\forall x\in \mathbb {R} ^{*}\setminus \{-1,1\}\quad I'\left(x\right)&=\int _{0}^{+\infty }{\frac {2x}{\left(x^{2}+t^{2}\right)\left(1+t^{2}\right)}}\,\mathrm {d} t\\&={\frac {2x}{x^{2}-1}}\int _{0}^{+\infty }\left({\frac {1}{1+t^{2}}}-{\frac {1}{x^{2}+t^{2}}}\right)\,\mathrm {d} t\\&={\frac {2x}{x^{2}-1}}\left(\int _{0}^{+\infty }{\frac {1}{1+t^{2}}}\,\mathrm {d} t-{\frac {1}{|x|}}\int _{0}^{+\infty }{\frac {1}{1+s^{2}}}\,\mathrm {d} s\right)\\&={\frac {2x}{x^{2}-1}}\left(1-{\frac {1}{|x|}}\right){\frac {\pi }{2}}\\&={\frac {x}{|x|}}{\frac {\pi }{|x|+1}}.\end{aligned}}$
Par continuité, cette expression de $I'\left(x\right)$ est encore valide pour $x=\pm 1$ .
$I\left(0\right)=2\int _{0}^{+\infty }{\frac {\ln t}{1+t^{2}}}\,\mathrm {d} t=2\int _{+\infty }^{0}{\frac {-\ln s}{1+1/s^{2}}}\,{\frac {-\mathrm {d} s}{s^{2}}}=-2\int _{0}^{+\infty }{\frac {\ln s}{s^{2}+1}}\,\mathrm {d} s=-I\left(0\right)$ donc $I\left(0\right)=0$ .
D'après la question 3, il existe une constante $C$ telle que $\forall x>0\quad I\left(x\right)=\pi \ln \left(x+1\right)+C$ . D'après les questions 1 et 4, $C=0$ .
Donc $I\left(x\right)=\pi \ln \left(x+1\right)$ pour tout $x\geq 0$ et par parité, $I\left(x\right)=\pi \ln \left(|x|+1\right)$ pour tout $x\in \mathbb {R}$ .

Exercice 2-7

Soient $F$ et $G$ définies sur $\mathbb {R}$ par

F(x)=\int _{0}^{x}\mathrm {e} ^{-t^{2}}\,\mathrm {d} t,\quad G(x)=\int _{0}^{1}{\frac {\mathrm {e} ^{-x^{2}(1+t^{2})}}{1+t^{2}}}\,\mathrm {d} t

.

Montrer que $F$ et $G$ sont de classe C¹ et calculer leurs dérivées.
En déduire que $G+F^{2}$ est constante. Que vaut cette constante ?
Déterminer la limite en $+\infty$ de $G$ puis de $F$ , et retrouver ainsi la valeur de l'intégrale de Gauss, $\int _{-\infty }^{+\infty }\mathrm {e} ^{-t^{2}}\,\mathrm {d} t$ .

Solution

- D'après le théorème fondamental de l'analyse, $F$ est de classe C¹ et $\forall x\in \mathbb {R} \quad F'(x)=\mathrm {e} ^{-x^{2}}$ .
- D'après le théorème adhoc sur les intégrales à paramètre, $G$ est de classe C¹ et $\forall x\in \mathbb {R} \quad G'(x)=-2x\int _{0}^{1}\mathrm {e} ^{-x^{2}(1+t^{2})}\,\mathrm {d} t$ .
Par changement de variable $s=xt$ , $G'(x)=-2\int _{0}^{1}\mathrm {e} ^{-x^{2}-s^{2}}\,\mathrm {d} s=-2F'(x)F(x)$ donc $(G+F^{2})'=0$ .
Par conséquent, $\forall x\in \mathbb {R} \quad (G+F^{2})(x)=(G+F^{2})(0)=0+\int _{0}^{1}{\frac {1}{1+t^{2}}}\,\mathrm {d} t=[\arctan ]_{0}^{1}={\frac {\pi }{4}}$ .
D'après le théorème adhoc sur les intégrales à paramètre (ou simplement parce que $0\leq G(x)\leq \mathrm {e} ^{-x^{2}}$ ), $\lim _{+\infty }G=0$ .
On déduit alors de la question précédente que $\lim _{+\infty }F^{2}={\frac {\pi }{4}}$ , c'est-à-dire (puisque $F\geq 0$ ) $\lim _{+\infty }F={\frac {\sqrt {\pi }}{2}}$ .
Par conséquent, $\int _{-\infty }^{+\infty }\mathrm {e} ^{-t^{2}}\,\mathrm {d} t=2\int _{0}^{+\infty }\mathrm {e} ^{-t^{2}}\,\mathrm {d} t=2\lim _{+\infty }F={\sqrt {\pi }}$ .

Variante : pour $x\geq 0$ , on pose

\psi (x)=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-(t^{2}+1)x}}{t^{2}+1}}\;\mathrm {d} t

.

Montrer que sur $\left[0,+\infty \right[$ , $\psi$ est bien définie et continue.
Montrer que $\psi$ est de classe C¹ sur $\left]0,+\infty \right[$ .
Calculer $\psi (0)$ et étudier la limite de $\psi$ en $+\infty$ .
Montrer que pour tout $x\in \mathbb {R} ^{*}$ on a $\psi '(x)=-{\frac {\mathrm {e} ^{-x}}{\sqrt {x}}}\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\;\mathrm {d} s$ .
Montrer que $\int _{0}^{+\infty }\psi '(x)\;\mathrm {d} x=-2\left(\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\;\mathrm {d} s\right)^{2}$ .
En déduire que $\int _{0}^{+\infty }\mathrm {e} ^{-u^{2}}\;\mathrm {d} u={\frac {\sqrt {\pi }}{2}}$ .

Solution

La fonction $(t,x)\mapsto {\frac {\mathrm {e} ^{-(t^{2}+1)x}}{t^{2}+1}}$ est continue sur $\mathbb {R} _{+}\times \mathbb {R} _{+}$ comme quotient de composées de fonctions usuelles dont le dénominateur ne s'annule pas.
En outre pour tout $(t,x)\in (\mathbb {R} _{+})^{2}$ on a $0\leq {\frac {\mathrm {e} ^{-(t^{2}+1)x}}{t^{2}+1}}\;\mathrm {d} t\leq {\frac {1}{1+t^{2}}}$ .
Or l'intégrale $\int _{0}^{+\infty }{\frac {1}{t^{2}+1}}\;\mathrm {d} t$ est convergente, donc par le théorème de continuité sous l'intégrale on obtient que $\psi$ est définie et continue sur $\mathbb {R} _{+}$ .
Soit $\varepsilon >0$ . Montrons que $\psi$ est dérivable sur $\left]\varepsilon ,+\infty \right[$ . Pour tout $t\in \mathbb {R} _{+}$ , l'application $x\mapsto {\frac {\mathrm {e} ^{-(t^{2}+1)x}}{t^{2}+1}}$ est de classe C¹ sur $\left]\varepsilon ,+\infty \right[$ .
En outre pour tout $(t,x)\in \mathbb {R} _{+}\times \left]\varepsilon ,+\infty \right[$ on a $\left|{\frac {\partial }{\partial x}}{\frac {\mathrm {e} ^{-(t^{2}+1)x}}{t^{2}+1}}\right|=\mathrm {e} ^{-(t^{2}+1)x}\leq \mathrm {e} ^{-(t^{2}+1)\varepsilon }$ .
Or l'intégrale $\int _{0}^{+\infty }\mathrm {e} ^{-(t^{2}+1)\varepsilon }\;\mathrm {d} t$ est convergente, donc par le théorème de dérivation sous l'intégrale, on obtient que $\psi$ est C¹ sur $\left]\varepsilon ,+\infty \right[$ et ce pour tout $\varepsilon >0$ donc en définitive sur $\left]0,+\infty \right[$ , et que sur cet intervalle,
$\psi '(x)=-\int _{0}^{+\infty }{\mathrm {e} ^{-(t^{2}+1)x}}\;\mathrm {d} t$ .
Remarquons que le « garde-fou » $\varepsilon >0$ était indispensable puisqu'en $0$ , $\psi$ n'est pas dérivable. En effet, $\lim _{x\to 0^{+}}\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-(t^{2}+1)x}-1}{x(t^{2}+1)}}\;\mathrm {d} t=-\infty$ car $\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-(t^{2}+1)x}-1}{x(t^{2}+1)}}\;\mathrm {d} t=\int _{x}^{+\infty }{\frac {\mathrm {e} ^{-s}-1}{s}}\;{\frac {\mathrm {d} s}{2x{\sqrt {{\frac {s}{x}}-1}}}}<{\frac {1}{2{\sqrt {x}}}}\int _{x}^{+\infty }{\frac {\mathrm {e} ^{-s}-1}{s^{3/2}}}\;\mathrm {d} s\sim _{x\to 0^{+}}-{\frac {C}{2{\sqrt {x}}}}$ avec $C=\int _{0}^{+\infty }{\frac {1-\mathrm {e} ^{-s}}{s^{3/2}}}\;\mathrm {d} s>0$ .
On a
$\psi (0)=\int _{0}^{+\infty }{\frac {1}{1+t^{2}}}\;\mathrm {d} t={\frac {\pi }{2}}$ .
Pour tout $x\geq 0$ on a
$0\leq \psi (x)\leq \int _{0}^{+\infty }{\frac {\mathrm {e} ^{-x}}{t^{2}+1}}\;\mathrm {d} t\leq {\frac {\pi }{2}}\mathrm {e} ^{-x}{\xrightarrow[{x\to {+\infty }}]{}}0$ .
Soit $x>0$ . On a vu que $\psi '(x)=-\int _{0}^{+\infty }\mathrm {e} ^{-(t^{2}+1)x}\;\mathrm {d} t=-\mathrm {e} ^{-x}\int _{0}^{+\infty }\mathrm {e} ^{-t^{2}x}\;\mathrm {d} t$ .
On effectue le changement de variable $s={\sqrt {x}}t$ , $\mathrm {d} s={\sqrt {x}}\;\mathrm {d} t$ , et l'on obtient
$\psi '(x)=-{\frac {\mathrm {e} ^{-x}}{\sqrt {x}}}\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\;\mathrm {d} s$ .
On a alors
$\int _{0}^{+\infty }\psi '(x)\;\mathrm {d} x=-\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-x}}{\sqrt {x}}}\;\mathrm {d} x\times \int _{0}^{+\infty }\mathrm {\mathrm {e} } ^{-s^{2}}\;\mathrm {d} s$ .
Dans la première intégrale, on effectue le changement de variables $x=s^{2}$ , $\mathrm {d} x=2s\;\mathrm {d} s$ , ce qui donne bien l'égalité demandée.
D'autre part on a
$\int _{0}^{+\infty }\psi '(x)\;\mathrm {d} x=\lim _{+\infty }\psi -\lim _{0}\psi =-{\frac {\pi }{2}}$
et donc
$\left(\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\;\mathrm {d} s\right)^{2}={\frac {\pi }{4}}$ .

Exercice 2-8

Toutes les fonctions considérées sont encore supposées continues par morceaux.

1. À l'aide des deux premiers théorèmes des rappels ci-dessus, démontrer la variante suivante du troisième :

Classe C¹, hypothèses faibles

Si :

il existe $x_{0}\in J$ tel que $f(x_{0},\cdot )$ soit (absolument) intégrable
$\forall t\in \left[a,b\right[\quad x\mapsto f(x,t)$ est de classe C¹ sur $J$ ;
$\forall (x,t)\in J\times \left[a,b\right[\quad \left|{\frac {\partial f}{\partial x}}(x,t)\right|\leq g(t)$ pour une certaine fonction $g$ intégrable sur $\left[a,b\right[$ ,

alors :

$F$ est bien définie et de classe C¹ sur $J$ et $\forall x\in J\quad F'(x)=\int _{a}^{b}{\frac {\partial f}{\partial x}}(x,t)\,\mathrm {d} t$ .

2. Démontrer la généralisation suivante, pour $k\in \mathbb {N}$ :

Classe C^k, hypothèses faibles

Si :

$\forall j\in \{0,1,\dots ,k-1\}\quad \exists x_{j}\in J\quad {\frac {\partial ^{j}f}{\partial x^{j}}}(x_{j},\cdot )$ est (absolument) intégrable sur $\left[a,b\right[$ ;
$\forall t\in \left[a,b\right[\quad f(\cdot ,t)$ est de classe C^k sur $J$ ;
$\forall x\in J\quad \left|{\frac {\partial ^{k}f}{\partial x^{k}}}(x,\cdot )\right|\leq g$ , intégrable sur $\left[a,b\right[$ ,

alors $F$ est bien définie et de classe C^k sur $J$ et $\forall j\leq k\quad \forall x\in J\quad F^{(j)}(x)=\int _{a}^{b}{\frac {\partial ^{j}f}{\partial x^{j}}}(x,t)\,\mathrm {d} t$ .

Solution

Remarquons d'abord que les hypothèses suffisent pour que pour tout $x\in J$ , $f(x,\cdot )$ soit intégrable (donc $F$ bien définie sur $J$ ). En effet, d'après le théorème des accroissements finis, $|f(x,t)|\leq |f(x_{0},t)|+\left|x-x_{0}\right|g(t)$ .
Fixons $x\in J$ et posons, pour tout $y\in J\setminus \{x\}$ : $h(y,t)={\frac {f(y,t)-f(x,t)}{y-x}}$ . Alors, $|h(\cdot ,t)|$ est dominée par $g(t)$ donc d'après le 1^er théorème des rappels (Limite), $\lim _{y\to x}\int _{a}^{b}h(y,t)\,\mathrm {d} t=\int _{a}^{b}\lim _{y\to x}h(y,t)\,\mathrm {d} t$ , c'est-à-dire $F'(x)=\int _{a}^{b}{\frac {\partial f}{\partial x}}(x,t)\,\mathrm {d} t$ .
De plus, $F'$ est continue d'après le 2^e théorème des rappels (Continuité).
Démontrons le théorème « Classe C^k » par récurrence sur k. Pour k = 0, il s'agit simplement du 2^e théorème (Continuité) des rappels. Supposons le théorème « Classe C^k » vrai pour un certain k ≥ 0, et soit $f$ une fonction vérifiant les hypothèses du théorème « Classe C^k+1 », en particulier $\left|{\frac {\partial ^{k+1}f}{\partial x^{k+1}}}(x,\cdot )\right|\leq g$ intégrable. En supposant (sans perte de généralité) que l'intervalle $J$ est borné, de longueur $L$ , on a alors (comme dans la question 1) $\left|{\frac {\partial ^{k}f}{\partial x^{k}}}(x,\cdot )\right|\leq \left|{\frac {\partial ^{k}f}{\partial x^{k}}}(x_{k},\cdot )\right|+Lg$ , intégrable donc (par hypothèse de récurrence) $F$ est bien définie et de classe C^k et $\forall j\leq k\quad \forall x\in J\quad F^{(j)}(x)=\int _{a}^{b}{\frac {\partial ^{j}f}{\partial x^{j}}}(x,t)\,\mathrm {d} t$ . On conclut en appliquant le théorème « Classe C¹ » à ${\frac {\partial ^{k}f}{\partial x^{k}}}$ .

Référence : Michel Stainer, « Intégrales dépendant d'un paramètres : démonstrations »

Exercice 2-9

Soient

H(x)=\int _{-\infty }^{+\infty }{\frac {\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t\quad {\text{et}}\quad F(x)=\int _{-\infty }^{+\infty }{\frac {\mathrm {e} ^{\mathrm {i} xt}}{1+t^{2}}}\,\mathrm {d} t

.

Montrer que $H$ est bien définie sur $\mathbb {R}$ et de classe C² et que $H-H''=F$ .
Montrer que $2H'(x)=-xF(x)$ (pour tout $x\in \mathbb {R}$ ).
Déduire des deux points précédents que sur $\mathbb {R} ^{*}$ $\R^*$ :
1. $F$ est dérivable et $xF'(x)=F(x)-2H(x)$ (pour tout $x\in \mathbb {R} ^{*}$ ), puis
2. $F$ est deux fois dérivable et $F''=F$ .
Calculer $F(0)$ et montrer que $F$ est bornée.
Déduire des questions 3.2 et 4 l'expression explicite de $F(x)$ pour tout $x\geq 0$ .
Donner les valeurs explicites des deux intégrales suivantes :
$\int _{0}^{+\infty }{\frac {\cos {t}}{1+t^{2}}}\,\mathrm {d} t\quad {\text{et}}\quad \int _{0}^{+\infty }{\frac {t\sin {t}}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t$ .

Solution

Posons $h(x,t)={\frac {\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}$ .
Pour tout $t\in \mathbb {R}$ , $h(\cdot ,t)$ est de classe C² sur $\mathbb {R}$ , ${\frac {\partial h}{\partial x}}(x,t)={\frac {\mathrm {i} t\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}$ et ${\frac {\partial ^{2}h}{\partial x^{2}}}(x,t)={\frac {-t^{2}\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}$ .
Pour tout $x\in \mathbb {R}$ , $h(x,\cdot )$ , ${\frac {\partial h}{\partial x}}(x,\cdot )$ et ${\frac {\partial ^{2}h}{\partial x^{2}}}(x,\cdot )$ sont localement intégrables (car continues) et
$|h(x,t)|={\frac {1}{\left(1+t^{2}\right)^{2}}},\left|{\frac {\partial h}{\partial x}}(x,t)\right|={\frac {|t|}{\left(1+t^{2}\right)^{2}}},\left|{\frac {\partial ^{2}h}{\partial x^{2}}}(x,t)\right|={\frac {t^{2}}{\left(1+t^{2}\right)^{2}}}$ sont fonctions seulement de $t$ et intégrables (par équivalent en l'infini et critère de Riemann).
$H$ est donc bien définie sur $\mathbb {R}$ et de classe C², et l'on a
$H'(x)=\int _{-\infty }^{+\infty }{\frac {\mathrm {i} t\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t\quad {\text{et}}\quad H''(x)=\int _{-\infty }^{+\infty }{\frac {-t^{2}\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t$ donc
$H(x)-H''(x)=\int _{-\infty }^{+\infty }(1+t^{2}){\frac {\mathrm {e} ^{\mathrm {i} xt}}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t=F(x)$ (ce qui prouve que $F$ est bien définie sur $\mathbb {R}$ et continue).
Par intégration par parties,
${\begin{aligned}2H'(x)&=\int _{-\infty }^{+\infty }{\frac {2t}{\left(1+t^{2}\right)^{2}}}\mathrm {i} \mathrm {e} ^{\mathrm {i} xt}\,\mathrm {d} t\\&=\left[{\frac {-1}{1+t^{2}}}\mathrm {i} \mathrm {e} ^{\mathrm {i} xt}\right]_{-\infty }^{+\infty }-\int _{-\infty }^{+\infty }{\frac {-1}{1+t^{2}}}\mathrm {i} ^{2}x\mathrm {e} ^{\mathrm {i} xt}\,\mathrm {d} t\\&=0-x\int _{-\infty }^{+\infty }{\frac {\mathrm {e} ^{\mathrm {i} xt}}{1+t^{2}}}\,\mathrm {d} t\\&=-xF(x).\end{aligned}}$
Sur $\mathbb {R} ^{*}$ $\R^*$ :
1. $x\mapsto F(x)=-{\frac {2H'(x)}{x}}$ est dérivable et (en dérivant l'équation obtenue dans 2 puis en utilisant 1)
  $-F(x)-xF'(x)=2H''(x)=2\left(H(x)-F(x)\right)$ , ce qui se simplifie en $xF'(x)=F(x)-2H(x)$ ;
2. $x\mapsto F'(x)={\frac {F(x)-2H(x)}{x}}$ est dérivable et (en dérivant l'équation obtenue au point précédent puis en utilisant 2)
  $F'(x)+xF''(x)=F'(x)-2H'(x)=F'(x)+xF(x)$ , autrement dit $F$ est deux fois dérivable et $F''=F$ .
$|F(x)|\leq F(0)=\int _{-\infty }^{+\infty }{\frac {\mathrm {d} t}{1+t^{2}}}=\left[\arctan t\right]_{-\infty }^{+\infty }=\pi$ .
D'après 3.2, pour tout $x>0$ et même (par continuité de $F$ en $0$ ) pour tout $x\geq 0$ , $F(x)=a\operatorname {e} ^{x}+b\operatorname {e} ^{-x}$ , pour certains nombres complexes $a$ et $b$ à déterminer.
D'après 4, $a+b=\pi$ et $a=0$ . Donc $\forall x\in \mathbb {R} _{+}\quad F(x)=\pi \operatorname {e} ^{-x}$ .
Par parité de $\cos$ et imparité de $\sin$ , $\int _{0}^{+\infty }{\frac {\cos t}{1+t^{2}}}\,\mathrm {d} t={\frac {F(1)}{2}}={\frac {\pi }{2\mathrm {e} }}$ et $\int _{0}^{+\infty }{\frac {t\sin t}{\left(1+t^{2}\right)^{2}}}\,\mathrm {d} t=-{\frac {H'(1)}{2}}={\frac {F(1)}{4}}={\frac {\pi }{4\mathrm {e} }}$ .

Exercice 2-10

On pose

f(x,t)={\frac {1-\cos(xt)}{t^{2}}}\operatorname {e} ^{-t}

et

F(x)=\int _{0}^{+\infty }f(x,t)\,\mathrm {d} t

.

Montrer que $F$ est (au moins) de classe C² sur $\mathbb {R}$ et calculer $F''$ , puis $F'$ , puis $F$ .

Solution

Pour tout $t\in \left]0,+\infty \right[$ , $f(\cdot ,t)$ est de classe C² sur $\mathbb {R}$ , ${\frac {\partial f}{\partial x}}(x,t)={\frac {\sin(xt)}{t}}\operatorname {e} ^{-t}$ et ${\frac {\partial ^{2}f}{\partial x^{2}}}(x,t)=\cos(xt)\operatorname {e} ^{-t}$ .

$f(0,t)={\frac {\partial f}{\partial x}}(0,t)=0$ .

$\left|{\frac {\partial ^{2}f}{\partial x^{2}}}(x,t)\right|\leq \operatorname {e} ^{-t}$ et $\int _{0}^{+\infty }\operatorname {e} ^{-t}\,\mathrm {d} t=1<\infty$ .

D'après le « théorème Classe C^k, hypothèses faibles », $F$ est donc de classe C² sur $\mathbb {R}$ et

$F''(x)=\int _{0}^{+\infty }\cos(xt)\operatorname {e} ^{-t}\,\mathrm {d} t=\operatorname {Re} \left(\int _{0}^{+\infty }\operatorname {e} ^{(x\mathrm {i} -1)t}\,\mathrm {d} t\right)=\operatorname {Re} \left({\frac {-1}{x\mathrm {i} -1}}\right)={\frac {1}{1+x^{2}}}$ donc (comme $F'(0)=0$ )

$F'=\arctan$ et (comme $F(0)=0$ )

$F(x)=\int _{0}^{x}\arctan u\,\mathrm {d} u=\left[u\arctan u\right]_{0}^{x}-\int _{0}^{x}{\frac {u}{1+u^{2}}}\,\mathrm {d} u=x\arctan x-{\frac {1}{2}}\ln \left(1+x^{2}\right)$ .

Exercice 2-11

Soit $f_{n}(t)=\cos ^{n}t$ . Montrer de deux façons que $\lim _{n\to +\infty }\int _{0}^{\pi /2}f_{n}(t)\;\mathrm {d} t=0$ :

en étudiant l'uniformité de la convergence de la suite de fonctions $f_{n}$ sur les intervalles de la forme $[\alpha ,\pi /2]$ avec $\alpha >0$ ;
en utilisant le théorème de convergence dominée.

Solution

$\forall t\in [\alpha ,\pi /2]\quad \cos t\in [0,\cos \alpha ]$ et $0\leq \cos \alpha <1$ donc $f_{n}\to 0$ uniformément sur $[\alpha ,\pi /2]$ donc $\int _{\alpha }^{\pi /2}f_{n}(t)\;\mathrm {d} t\to 0$ donc pour $n$ suffisamment grand, $\int _{\alpha }^{\pi /2}f_{n}(t)\;\mathrm {d} t\leq \alpha$ et alors, $\int _{0}^{\pi /2}f_{n}(t)\;\mathrm {d} t\leq 2\alpha$ .
Soit $f(t)=0$ si $t\in \left]0,\pi /2\right]$ et $f(0)=1$ . Alors, $f_{n}\to f$ simplement sur $[0,\pi /2]$ et $|f_{n}|\leq 1$ (intégrable sur le segment) donc par convergence dominée, $\int _{0}^{\pi /2}f_{n}(t)\;\mathrm {d} t\to \int _{0}^{\pi /2}f(t)\;\mathrm {d} t=0$ .

Exercice 2-12

Justifier la convergence des intégrales $I_{n}:=\int _{0}^{+\infty }\mathrm {e} ^{-t}\sin ^{n}t\;\mathrm {d} t$ et étudier $\lim _{n\to +\infty }I_{n}$ .
Soient $f$ une fonction continue sur $[0,1]$ et $I_{n}:=\int _{0}^{1}f(t^{n})\;\mathrm {d} t$ . Étudier $\lim _{n\to +\infty }I_{n}$ .
Calculer $\lim _{n\to +\infty }\int _{0}^{+\infty }{\frac {\sin(\pi x)}{1+x^{n}}}\;\mathrm {d} x$ .

Solution

$f_{n}(t):=\mathrm {e} ^{-t}\sin ^{n}t\to 0$ pour tout $t\notin {\frac {\pi }{2}}+\mathbb {Z} \pi$ donc pour presque tout $t$ . D'autre part, pour tout $n\in \mathbb {N}$ , $|f_{n}(t)|\leq \mathrm {e} ^{-t}$ , dont l'intégrale de $0$ à $+\infty$ converge. Par conséquent, les intégrales $I_{n}$ sont convergentes et leur limite est $0$ .
$f(t^{n})\to f(0)$ pour tout $t\in [0,1[$ . D'autre part, $|f(t^{n})|\leq \max _{s\in [0,1]}|f(s)|$ , fonction constante donc intégrable sur le segment. Donc $I_{n}\to \int _{0}^{1}f(0)\;\mathrm {d} t=f(0)$ .
Quand $n\to +\infty$ , ${\frac {\sin(\pi x)}{1+x^{n}}}$ tend vers $0$ si $x\geq 1$ et vers $\sin(\pi x)$ si $0\leq x<1$ . De plus, à partir de $n=2$ , $\left|{\frac {\sin(\pi x)}{1+x^{n}}}\right|\leq {\frac {1}{1+x^{2}}}$ , intégrable. Donc $\lim _{n\to +\infty }\int _{0}^{+\infty }{\frac {\sin(\pi x)}{1+x^{n}}}\;\mathrm {d} x=\int _{0}^{+\infty }\sin(\pi x)\;\mathrm {d} x={\frac {2}{\pi }}$ .

Exercice 2-13

L'objectif est de calculer $I:=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t$ .

Pour $x\geq 0$ , on pose $F(x):=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}\;\mathrm {d} t$ .

Justifier que $F$ est bien définie.
Montrer que $F$ est dérivable et solution d'une équation différentielle linéaire d'ordre $1$ avec second membre.
En déduire que $F(x)=\mathrm {e} ^{x}\left(F(0)-\int _{0}^{x}{\frac {\mathrm {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t\right)$ .
Calculer $F(0)$ .
Montrer que $\lim _{+\infty }F=0$ . En déduire la valeur de $I$ .
Retrouver ainsi la valeur de l'intégrale de Gauss, $\int _{-\infty }^{+\infty }\mathrm {e} ^{-s^{2}}\,\mathrm {d} s$ .

Solution

$t\mapsto {\frac {\mathrm {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}$ est continue (donc localement intégrable) sur $\left]0,+\infty \right[$ et pour tout $x\geq 0$ , $0<{\frac {\mathrm {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}<{\frac {1}{(1+t){\sqrt {t}}}}$ , dont l'intégrale de $0$ à $+\infty$ converge.
$\left|{\frac {\partial }{\partial x}}\left({\frac {\operatorname {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}\right)\right|=\left|{\frac {-t\operatorname {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}\right|\leq {\frac {{\sqrt {t}}\operatorname {e} ^{-\varepsilon t}}{1+t}}$ pour $x\geq \varepsilon >0$ . Donc $F$ est dérivable sur $\cup _{\varepsilon >0}\left]\varepsilon ,+\infty \right[=\left]0,+\infty \right[$ et
$F'(x)=\int _{0}^{+\infty }{\frac {-t\operatorname {e} ^{-xt}}{\left(1+t\right){\sqrt {t}}}}\;\mathrm {d} t$ , d'où $F(x)-F'(x)=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-xt}}{\sqrt {t}}}\;\mathrm {d} t={\frac {I}{\sqrt {x}}}$ .
Variation de la constante : $F(x)=C(x)\operatorname {e} ^{x}$ avec $-C'(x)\operatorname {e} ^{x}={\frac {I}{\sqrt {x}}}$ , c.-à-d. $C'(x)=-{\frac {I\operatorname {e} ^{-x}}{\sqrt {x}}}$ .
Donc $\operatorname {e} ^{-x}F(x)-\operatorname {e} ^{0}F(0)=C(x)-C(0)=-I\int _{0}^{x}{\frac {\operatorname {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t$ , ce qui donne bien $F(x)=\mathrm {e} ^{x}\left(F(0)-\int _{0}^{x}{\frac {\mathrm {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t\right)$ .
$F(0)=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{\left(1+t\right){\sqrt {t}}}}=\int _{0}^{+\infty }{\frac {2{\cancel {s}}\mathrm {d} s}{\left(1+s^{2}\right){\cancel {s}}}}=\pi$ .
$0<F(x)\leq \int _{0}^{+\infty }{\frac {\mathrm {e} ^{-xt}}{\sqrt {t}}}\;\mathrm {d} t={\frac {I}{\sqrt {x}}}$ donc $\lim _{+\infty }F=0$ et a fortiori, $\lim _{x\to +\infty }F(x)\operatorname {e} ^{-x}=0$ , c.-à-d. (d'après la question 3)
$I\lim _{x\to +\infty }\int _{0}^{x}{\frac {\mathrm {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t=F(0)$ . Ceci équivaut à $I^{2}=\pi$ , soit $I={\sqrt {\pi }}$ .
${\sqrt {\pi }}=I=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-t}}{\sqrt {t}}}\;\mathrm {d} t=2\int _{0}^{+\infty }\mathrm {e} ^{-s^{2}}\;\mathrm {d} s=\int _{-\infty }^{+\infty }\mathrm {e} ^{-s^{2}}\,\mathrm {d} s$ .

Exercice 2-14

Pour $x\geq 0$ , on pose $F(x)=\int _{0}^{+\infty }{\frac {1-\cos t}{t^{2}}}\operatorname {e} ^{-xt}\;\mathrm {d} t$ .

Montrer que $F$ est définie et continue sur $\mathbb {R} _{+}$ .
Montrer que $F$ est de classe C² sur $\mathbb {R} _{+}^{*}$ et que $\lim _{+\infty }F'=0$ .
En déduire l'expression explicite de $F''$ puis $F'$ , puis la limite de $F'$ en $0^{+}$ .
Retrouver directement cette limite.

Solution

$x\mapsto {\frac {1-\cos t}{t^{2}}}\operatorname {e} ^{-xt}$ est continue (et même C^∞) sur $\mathbb {R} _{+}$ pour tout $t>0$ et $0\leq {\frac {1-\cos t}{t^{2}}}\operatorname {e} ^{-xt}\leq {\frac {1-\cos t}{t^{2}}}$ , dont l'intégrale de $0$ à $+\infty$ converge. Donc $F$ est continue sur $\mathbb {R} _{+}$ .
$F$ est C² sur $\mathbb {R} _{+}^{*}$ et pour tout $x>0$ , $F'(x)=\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t$ . En effet, pour tout $x\geq \varepsilon >0$ (et tout $t>0$ ), ${\frac {1-\cos t}{t}}$ est positif et (d'après le théorème des accroissements finis) majoré par $1$ , donc $\left|{\frac {\partial }{\partial x}}\left({\frac {1-\cos t}{t^{2}}}\operatorname {e} ^{-xt}\right)\right|=\left|{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\right|\leq \operatorname {e} ^{-\varepsilon t}$ , dont l'intégrale de $0$ à $+\infty$ converge. Cette majoration permet de plus d'affirmer que $\lim _{+\infty }F'=\int _{0}^{+\infty }\lim _{x\to +\infty }{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t=\int _{0}^{+\infty }0\;\mathrm {d} t=0$ . Ou plus élémentairement : $-F'(x)$ est positif et majoré par $\int _{0}^{+\infty }\operatorname {e} ^{-xt}\;\mathrm {d} t={\frac {1}{x}}$ , donc $\lim _{+\infty }F'=0$ .
De même, $\left|{\frac {\partial }{\partial x}}\left({\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\right)\right|=\left(1-\cos t\right)\operatorname {e} ^{-xt}\leq \operatorname {e} ^{-\varepsilon t}$ et pour tout $x>0$ , $F''(x)=\int _{0}^{+\infty }(1-\cos t)\operatorname {e} ^{-xt}\;\mathrm {d} t$ .
$F''(x)=\int _{0}^{+\infty }\operatorname {e} ^{-xt}\;\mathrm {d} t-\int _{0}^{+\infty }\operatorname {Re} \left(\operatorname {e} ^{(\mathrm {i} -x)t}\right)\;\mathrm {d} t={\frac {1}{x}}+\operatorname {Re} \left({\frac {1}{\mathrm {i} -x}}\right)={\frac {1}{x}}-{\frac {x}{x^{2}+1}}$ .
$F'(x)=C+\ln x-{\frac {1}{2}}\ln \left(x^{2}+1\right)=C-\ln {\frac {\sqrt {x^{2}+1}}{x}}$ avec $C=\lim _{+\infty }F'=0$ , soit $F'(x)=-{\frac {1}{2}}\ln \left(1+{\frac {1}{x^{2}}}\right)$ , donc $\lim _{0}F'=-\infty$ .
Pour tout $t>0$ , $x\mapsto {\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}$ est croissante donc par convergence monotone, $\lim _{x\to 0^{+}}\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t=\int _{0}^{+\infty }\lim _{x\to 0^{+}}{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t=\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\;\mathrm {d} t$
ou plus élémentairement : $\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t\leq \int _{0}^{1/x}{\frac {\cos t-1}{t}}\operatorname {e} ^{-xt}\;\mathrm {d} t\leq \operatorname {e} ^{-1}\int _{0}^{1/x}{\frac {\cos t-1}{t}}\;\mathrm {d} t\,{\xrightarrow[{x\to 0^{+}}]{}}\operatorname {e} ^{-1}\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\;\mathrm {d} t$ .
Or $\int _{0}^{+\infty }{\frac {\cos t-1}{t}}\;\mathrm {d} t\leq \int _{1}^{+\infty }{\frac {\cos t-1}{t}}\;\mathrm {d} t=\int _{1}^{+\infty }{\frac {\cos t}{t}}\;\mathrm {d} t-\int _{1}^{+\infty }{\frac {\mathrm {d} t}{t}}=\int _{1}^{+\infty }{\frac {\cos t}{t}}\;\mathrm {d} t-(+\infty )=-\infty$ , donc $\lim _{0}F'=-\infty$ .

Exercice 2-15

Soit $J:\mathbb {R} \to \mathbb {R} ,\;x\mapsto \int _{0}^{\pi }\cos(x\cos \theta )\;\mathrm {d} \theta$ .

Montrer que $J$ est de classe C² et donner les expressions intégrales de $J'$ et $J''$ .
Vérifier que $\forall x\in \mathbb {R} \quad x\left(J(x)+J''(x)\right)=-J'(x)$ .
On admet que de même, la fonction
$K:\left]0,+\infty \right[\to \mathbb {R} ,\;x\mapsto \int _{0}^{\pi }\sin(x\sin \theta )\;\mathrm {d} \theta -2\int _{0}^{+\infty }\operatorname {e} ^{-x\sinh t}\;\mathrm {d} t$
est de classe C² et vérifie $\forall x\in \left]0,+\infty \right[\quad x\left(K(x)+K''(x)\right)=-K'(x)$ . Quel en est l'intérêt ?

Solution

$J$ est même C^∞ puisque $x\mapsto \cos(x\cos \theta )$ l'est et qu'on intègre sur un segment.
$J'(x)=-\int _{0}^{\pi }\cos \theta \sin(x\cos \theta )\;\mathrm {d} \theta$ et $J''(x)=-\int _{0}^{\pi }\cos ^{2}\theta \cos(x\cos \theta )\;\mathrm {d} \theta$ .
$x\left(J(x)+J''(x)\right)=x\int _{0}^{\pi }(1-\cos ^{2}\theta )\cos(x\cos \theta )\;\mathrm {d} \theta =\int _{0}^{\pi }x\sin ^{2}\theta \cos(x\cos \theta )\;\mathrm {d} \theta$
$=-\int _{0}^{\pi }\sin \theta {\frac {\mathrm {d} }{\mathrm {d} \theta }}\sin(x\cos \theta )\;\mathrm {d} \theta =-\left[\sin \theta \sin(x\cos \theta )\right]_{0}^{\pi }+\int _{0}^{\pi }\cos \theta \sin(x\cos \theta )\;\mathrm {d} \theta =0-J'(x)$ .
L'intérêt est que $(J,K)$ forme alors une base du plan vectoriel des solutions sur $\left]0,+\infty \right[$ de $xy''+y'+xy=0$ . En effet, elle est libre, puisque $J(0)\neq 0$ et $\lim _{0}K=-\infty$ (par convergence monotone pour la seconde intégrale dans $K$ , ou par minoration explicite : $\int _{0}^{+\infty }\operatorname {e} ^{-x\sinh t}\;\mathrm {d} t\geq \operatorname {e} ^{-1}\operatorname {arsinh} (1/x)$ ).

Exercice 2-16

Soient $f:\mathbb {R} ^{2}\to \mathbb {R}$ une fonction de classe C² et ${\displaystyle \varphi$ la fonction définie par

\varphi (x,y,z)=\int _{0}^{2\pi }f(x+z\cos \theta ,y+z\sin \theta )\;\mathrm {d} \theta

.

Montrer que $\varphi$ est bien définie et de classe C² et que

z\left({\frac {\partial ^{2}\varphi }{\partial x^{2}}}+{\frac {\partial ^{2}\varphi }{\partial y^{2}}}-{\frac {\partial ^{2}\varphi }{\partial z^{2}}}\right)-{\frac {\partial \varphi }{\partial z}}=0

.

Solution

\partial _{x}\varphi (x,y,z)=\int _{0}^{2\pi }\partial _{x}f(x+z\cos \theta ,y+z\sin \theta )\;\mathrm {d} \theta

\partial _{xx}\varphi (x,y,z)=\int _{0}^{2\pi }\partial _{xx}f(x+z\cos \theta ,y+z\sin \theta )\;\mathrm {d} \theta

\partial _{yy}\varphi (x,y,z)=\int _{0}^{2\pi }\partial _{yy}f(x+z\cos \theta ,y+z\sin \theta )\;\mathrm {d} \theta

\partial _{z}\varphi (x,y,z)=\int _{0}^{2\pi }{\big (}\cos \theta \,\partial _{x}f(x+z\cos \theta ,y+z\sin \theta )+\sin \theta \,\partial _{y}f(x+z\cos \theta ,y+z\sin \theta ){\big )}\;\mathrm {d} \theta

\partial _{zz}\varphi (x,y,z)=\int _{0}^{2\pi }{\big (}\cos ^{2}\theta \,\partial _{xx}f+2\cos \theta \sin \theta \partial _{xy}f+\sin ^{2}\theta \,\partial _{yy}f{\big )}\;\mathrm {d} \theta

\partial _{xx}f+\partial _{yy}f-\partial _{zz}f=\int _{0}^{2\pi }{\big (}\sin ^{2}\theta \,\partial _{xx}f+\cos ^{2}\theta \,\partial _{yy}f-2\cos \theta \sin \theta \partial _{xy}f{\big )}\;\mathrm {d} \theta

et par IPP :

\partial _{z}\varphi =\int _{0}^{2\pi }{\big (}z\sin ^{2}\theta \partial _{xx}f-z\sin \theta \cos \theta \partial _{xy}f{\big )}\;\mathrm {d} \theta +\int _{0}^{2\pi }{\big (}z\cos ^{2}\theta \partial _{yy}f-z\sin \theta \cos \theta \partial _{xy}f{\big )}\;\mathrm {d} \theta

.

Exercice 2-17

Soit $x\in \mathbb {R}$ . Montrer que l'intégrale $\int _{0}^{+\infty }\operatorname {e} ^{-t^{2}}\cos(tx)\;\mathrm {d} t$ est convergente. On note alors $\varphi (x)$ sa valeur.
Montrer que la fonction $\varphi$ est de classe C¹ (sur $\mathbb {R}$ ).
Montrer que $\varphi '(x)=-{\frac {x\varphi (x)}{2}}$ (pour tout $x\in \mathbb {R}$ ).
En déduire que $\varphi (x)={\frac {\sqrt {\pi }}{2}}\operatorname {e} ^{-x^{2}/4}$ , connaissant la valeur de l'intégrale de Gauss ( $\int _{0}^{+\infty }\mathrm {e} ^{-t^{2}}\,\mathrm {d} t={\frac {\sqrt {\pi }}{2}}$ ).

Solution

Convergence absolue.
$\left|{\frac {\partial }{\partial x}}\left(\operatorname {e} ^{-t^{2}}\cos(tx)\right)\right|=\left|-t\operatorname {e} ^{-t^{2}}\sin(tx)\right|\leq t\operatorname {e} ^{-t^{2}}\in \mathrm {L} ^{1}(\mathbb {R} _{+})$ donc $\varphi$ est de classe C¹ et $\varphi '(x)=-\int _{0}^{+\infty }t\operatorname {e} ^{-t^{2}}\sin(tx)\;\mathrm {d} t$ .
Par IPP, $\varphi '(x)=\left[{\frac {\operatorname {e} ^{-t^{2}}}{2}}\sin(tx)\right]_{0}^{+\infty }-{\frac {x}{2}}\int _{0}^{+\infty }\operatorname {e} ^{-t^{2}}\cos(tx)\;\mathrm {d} t=-{\frac {x\varphi (x)}{2}}$ .
On résout $\varphi '(x)+{\frac {x\varphi (x)}{2}}=0$ . Les solutions sont $\varphi (x)=C\operatorname {e} ^{-x^{2}/4}$ , avec ici $C=\varphi (0)={\frac {\sqrt {\pi }}{2}}$ .

Exercice 2-18

Pour $x\geq 0$ on pose $F(x)=\int _{0}^{+\infty }{\frac {\sin t}{t+x}}\;\mathrm {d} t$ .

Montrer que $F$ est continue, décroissante et que $F(x)=2\int _{0}^{+\infty }{\frac {\sin ^{2}(t/2)}{(t+x)^{2}}}\;\mathrm {d} t$ .
Montrer que $F$ est dérivable sur $\mathbb {R} _{+}^{*}$ et calculer sa dérivée.
Est-elle dérivable à droite en $0$ ?

Solution

$F(x)=\left[{\frac {1-\cos t}{t+x}}\right]_{0}^{+\infty }+\int _{0}^{+\infty }{\frac {1-\cos t}{(t+x)^{2}}}\;\mathrm {d} t=\int _{0}^{+\infty }{\frac {1-\cos t}{(t+x)^{2}}}\;\mathrm {d} t=2\int _{0}^{+\infty }{\frac {\sin ^{2}(t/2)}{(t+x)^{2}}}\;\mathrm {d} t$ .
Avec cette deuxième expression on voit que $F$ est continue et décroissante.
Puisque $0\leq {\frac {\sin ^{2}(t/2)}{(t+x)^{3}}}\leq {\frac {1}{(t+\varepsilon )^{3}}}$ pour $x>\varepsilon >0$ , on en déduit aussi que pour tout $x>0$ , $F'(x)=-4\int _{0}^{+\infty }{\frac {\sin ^{2}(t/2)}{(t+x)^{3}}}\;\mathrm {d} t$ .
Non car ${\frac {F(x)-F(0)}{x}}=-\int _{0}^{+\infty }{\frac {\sin t}{t(t+x)}}\;\mathrm {d} t{\xrightarrow[{x\to 0^{+}}]{}}-\infty$ ${\frac {F(x)-F(0)}{x}}=-\int _{0}^{+\infty }{\frac {\sin t}{t(t+x)}}\;\mathrm {d} t{\xrightarrow[{x\to 0^{+}}]{}}-\infty$ . En effet, on a (par exemple) :
- d'une part $-\int _{0}^{\frac {\pi }{4}}{\frac {\sin t}{t(t+x)}}\;\mathrm {d} t{\xrightarrow[{x\to 0^{+}}]{}}-\infty$ par convergence monotone et parce qu'en $0^{+}$ , $-{\frac {\sin t}{t^{2}}}$ est équivalent à $-{\frac {1}{t}}$ , négatif et dont l'intégrale diverge, ou plus calculatoirement : parce que $-\int _{0}^{\frac {\pi }{4}}{\frac {\sin t}{t(t+x)}}\;\mathrm {d} t\leq -{\frac {1}{\sqrt {2}}}\int _{0}^{\frac {\pi }{4}}{\frac {1}{t+x}}\;\mathrm {d} t=-{\frac {1}{\sqrt {2}}}\ln \left(1+{\frac {\pi }{4x}}\right){\xrightarrow[{x\to 0^{+}}]{}}-\infty$ ;
- d'autre part $-\int _{\frac {\pi }{4}}^{+\infty }{\frac {\sin t}{t(t+x)}}\;\mathrm {d} t\leq \int _{\frac {\pi }{4}}^{+\infty }{\frac {1}{t^{2}}}\;\mathrm {d} t={\frac {4}{\pi }}<+\infty$ .

Exercice 2-19

Pour tout l'exercice on fixe $a\in \left]0,1\right[$ . On note

\forall x\in \left]0,+\infty \right[\quad f(x)={\frac {1}{x}}\ln {\frac {1+x}{1+ax}}

et

\forall y\in \mathbb {R} _{+}\quad F(y)=\int _{1}^{1/a}{\frac {\ln(y+t)}{t}}\;\mathrm {d} t

.

Calculer $F(0)$ .
Montrer que $F$ est de classe C¹ sur $\mathbb {R} _{+}$ et donner une expression pour $F'$ ne faisant pas intervenir d'intégrale.
Montrer que $\forall y\in \mathbb {R} _{+}\quad F(y)={\frac {\ln ^{2}a}{2}}+\int _{0}^{y}f(x)\;\mathrm {d} x$ .

Solution

$F(0)=\int _{0}^{-\ln a}s\;\mathrm {d} s={\frac {\ln ^{2}a}{2}}$ .
Cf. exercice 2-8 ci-dessus. $y\mapsto {\frac {\ln(y+t)}{t}}$ est C¹ sur $\mathbb {R} _{+}$ (pour tout $t\in [1,1/a]$ ) et $\forall y\in \mathbb {R} _{+}\quad \forall t\in [1,1/a]\quad {\frac {1}{t(y+t)}}\leq {\frac {1}{t^{2}}}$ , intégrable sur $[1,1/a]$ donc $F$ est de classe C¹ sur $\mathbb {R} _{+}$ et $F'(y)=\int _{1}^{1/a}{\frac {1}{t(y+t)}}\;\mathrm {d} t$ . En particulier $F'(0)=1-a$ et pour tout $y>0$ , $F'(y)={\frac {1}{y}}\int _{1}^{1/a}\left({\frac {1}{t}}-{\frac {1}{y+t}}\right)\;\mathrm {d} t={\frac {1}{y}}\left[\ln {\frac {t}{y+t}}\right]_{1}^{1/a}=f(y)$ .
$F(y)=F(0)+\int _{0}^{y}F'(x)\;\mathrm {d} x$ .

Exercice 2-20

On pose $I(x)=\int _{0}^{\pi /2}\ln(\cos ^{2}t+x^{2}\sin ^{2}t)\,\mathrm {d} t$ .

Montrer que $I$ est de classe C¹ sur $\mathbb {R} _{+}^{*}$ .
Calculer $I'(x)$ .
En déduire $I(x)$ .

Solution

$x\mapsto \ln(\cos ^{2}t+x^{2}\sin ^{2}t)$ est C¹ pour tout $t\in \left[0,\pi /2\right[$ , et si $0<\varepsilon \leq x\leq M$ alors $\left|{\frac {\partial \ln(\cos ^{2}t+x^{2}\sin ^{2}t)}{\partial x}}\right|=\left|{\frac {2x\sin ^{2}t}{\cos ^{2}t+x^{2}\sin ^{2}t}}\right|\leq {\frac {2M\sin ^{2}t}{\cos ^{2}t+\varepsilon ^{2}\sin ^{2}t}}$ , continue sur $[0,\pi /2]$ donc intégrable.
Pour tout $x>0$ ,
${\begin{aligned}I'(x)&=2x\int _{0}^{\pi /2}{\frac {\sin ^{2}t}{\cos ^{2}t+x^{2}\sin ^{2}t}}\,\mathrm {d} t=2x\int _{0}^{\pi /2}{\frac {\mathrm {d} t}{\cot ^{2}t+x^{2}}}=2x\int _{+\infty }^{0}{\frac {-\mathrm {d} u}{(u^{2}+x^{2})(1+u^{2})}}\\&={\frac {2x}{x^{2}-1}}\int _{0}^{+\infty }\left({\frac {1}{1+u^{2}}}-{\frac {1}{u^{2}+x^{2}}}\right)\,\mathrm {d} u={\frac {2x}{x^{2}-1}}\left[\arctan u-{\frac {1}{x}}\arctan {\frac {u}{x}}\right]_{0}^{+\infty }={\frac {2x}{x^{2}-1}}\left(1-{\frac {1}{x}}\right){\frac {\pi }{2}}={\frac {\pi }{x+1}}.\end{aligned}}$
$I(1)=0$ donc pour tout $x>0$ , $I(x)=\int _{1}^{x}{\frac {\pi }{y+1}}\,\mathrm {d} y=\pi \ln {\frac {x+1}{2}}$ .
Remarque : on a bien $I(x)>0$ si $x>1$ et $I(x)<0$ si $x<1$ , ce qui était prévisible dès le départ.

Exercice 2-21

On pose $F(x)=\int _{0}^{+\infty }\operatorname {e} ^{-xt}\arctan t\,\mathrm {d} t$ .

Montrer que $F$ est bien définie sur $\mathbb {R} _{+}^{*}$ .
Pour $x>0$ on pose $G(x)=xF(x)$ . Montrer que $G(x)=\int _{0}^{+\infty }{\frac {\operatorname {e} ^{-xt}}{1+t^{2}}}\,\mathrm {d} t$ .
Montrer que $G$ est de classe C² sur $\mathbb {R} _{+}^{*}$ .
En déduire que $F$ est de classe C² sur $\mathbb {R} _{+}^{*}$ et que
$\forall x>0\quad xF''(x)+2F'(x)+xF(x)={\frac {1}{x}}$ .

Solution

$|\arctan |\leq \pi /2$ .
$G(x)=\int _{0}^{+\infty }x\operatorname {e} ^{-xt}\arctan t\,\mathrm {d} t=\underbrace {\left[-\operatorname {e} ^{-xt}\arctan t\right]_{0}^{+\infty }} _{0}+\int _{0}^{+\infty }{\frac {\operatorname {e} ^{-xt}}{1+t^{2}}}\,\mathrm {d} t$
$x\mapsto {\frac {\operatorname {e} ^{-xt}}{1+t^{2}}}$ est C², $\left|{\frac {\partial }{\partial x}}{\frac {\operatorname {e} ^{-xt}}{1+t^{2}}}\right|=\left|{\frac {-t\operatorname {e} ^{-xt}}{1+t^{2}}}\right|\leq {\frac {\operatorname {e} ^{-xt}}{2}}$ , $\left|{\frac {\partial ^{2}}{\partial x^{2}}}{\frac {\operatorname {e} ^{-xt}}{1+t^{2}}}\right|=\left|{\frac {t^{2}\operatorname {e} ^{-xt}}{1+t^{2}}}\right|\leq \operatorname {e} ^{-xt}$ , et pour $x\geq \varepsilon >0$ , $0<\operatorname {e} ^{-xt}\leq \operatorname {e} ^{-\varepsilon t}$ , dont l'intégrale de $0$ à $+\infty$ converge. Donc $G$ est C² sur $\mathbb {R} _{+}^{*}$ .
Donc $F$ est C² sur $\mathbb {R} _{+}^{*}$ et pour tout $x>0$ , $G'(x)=F(x)+xF'(x)$ et $G''(x)=2F'(x)+xF''(x)$ , si bien que $xF''(x)+2F'(x)+xF(x)=G''(x)+G(x)=\int _{0}^{+\infty }\operatorname {e} ^{-xt}\,\mathrm {d} t={\frac {1}{x}}$ .

Exercice 2-22

Pour tout réel $x>0$ , on note

\psi (x)=\int _{0}^{+\infty }{\frac {\sin t}{t^{2}+x^{2}}}\,\mathrm {d} t

.

Montrer que $\psi$ est bien définie et dérivable sur $\mathbb {R} _{+}^{*}$ .
Déterminer sa limite en $+\infty$ .

Solution

$x\mapsto {\frac {\sin t}{t^{2}+x^{2}}}$ est C¹ sur $\mathbb {R} _{+}^{*}$ et pour tout $x\geq \varepsilon >0$ , $\left|{\frac {\sin t}{t^{2}+x^{2}}}\right|\leq {\frac {1}{t^{2}+\varepsilon ^{2}}}$ et $\left|{\frac {-2x\sin t}{(t^{2}+x^{2})^{2}}}\right|\leq {\frac {2x|t|}{(t^{2}+x^{2})^{2}}}\leq {\frac {1}{t^{2}+\varepsilon ^{2}}}$ , dont l'intégrale de $0$ à $+\infty$ converge. Donc $\psi$ est bien définie et C¹ sur $\mathbb {R} _{+}^{*}$ .
Remarque : une étude de variations permet de remplacer le second majorant, plus finement, par une fonction a fortiori elle aussi intégrable de $0$ à $+\infty$ : $\sup _{x\geq \varepsilon }{\frac {2x|\sin t|}{(t^{2}+x^{2})^{2}}}={\begin{cases}{\frac {2\varepsilon |\sin t|}{(t^{2}+\varepsilon ^{2})^{2}}}&{\text{si }}t\leq \varepsilon {\sqrt {3}}\\\left({\frac {\sqrt {3}}{2}}\right)^{3}{\frac {|\sin t|}{t^{3}}}&{\text{si }}t\geq \varepsilon {\sqrt {3}}.\end{cases}}$ ou inversement, moins finement (mais encore par une fonction intégrable) : ${\frac {2M}{(t^{2}+\varepsilon ^{2})^{2}}}$ , si $0<\varepsilon \leq x\leq M$ .
La première de toutes les majorations ci-dessus permet d'affirmer de plus que $\lim _{+\infty }\psi =\int _{0}^{+\infty }\lim _{x\to +\infty }{\frac {\sin t}{t^{2}+x^{2}}}\,\mathrm {d} t=\int _{0}^{+\infty }0\,\mathrm {d} t=0$ . Ou plus élémentairement : $|\psi (x)|\leq \int _{0}^{+\infty }{\frac {1}{t^{2}+x^{2}}}\,\mathrm {d} t={\frac {\pi }{2x}}{\xrightarrow[{x\to +\infty }]{}}0$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.