Dans tout ce cours, ${\displaystyle a<b}$ sont des réels.
L'idée intuitive d'intégrale d'une fonction est celle "d'aire sous sa courbe" (au moins pour une fonction positive). Nous allons ici donner une façon de construire théoriquement l'intégrale à partir de cette idée (il existe d'autres constructions comme notamment celle de Lebesgue).
En fait, si ${\displaystyle f}$ est une fonction continue et positive sur un intervalle ${\displaystyle [a;b]}$ et si ${\displaystyle {\mathcal {C}}}$ est sa courbe représentative dans un repère, alors on veut que l’aire ${\displaystyle {\mathcal {A}}}$ de la surface (grisée sur le dessin) délimitée par :

${\displaystyle \left\{{\begin{array}{l}x=a{\textrm {~:~droite~verticale}}\\x=b{\textrm {~:~droite~verticale}}\\y=0{\textrm {~:~axe~des~abscisses}}\\C:y=f(x){\textrm {~:~courbe~de~}}f\\\end{array}}\right.}$

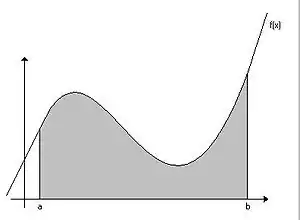
soit : ${\displaystyle {\mathcal {A}}=\int _{a}^{b}f(x)~\mathrm {d} x}$.

(Il manque des illustrations)

Intégrale d'une fonction en escalier

Définition : fonction en escalier

Une fonction ${\displaystyle f:[a;b]\to \mathbb {R} }$ est dite en escalier si, et seulement si, il existe une subdivision de ${\displaystyle [a;b]}$ adaptée à ${\displaystyle f}$ , c'est-à-dire un ensemble de points (subdivision) de ${\displaystyle [a;b]}$ tel que :

• ${\displaystyle a=a_{1}<a_{2}<\cdots <a_{n}=b\;\;(n\in \mathbb {N} )}$ ;
• ${\displaystyle f}$ est constante sur chaque intervalle ${\displaystyle ]a_{i};a_{i+1}[\,\forall i\in [1;n]\cap \mathbb {N} }$ .

Notation : on notera ${\displaystyle {\mathcal {E}}([a;b])}$ l’ensemble des fonctions en escalier sur ${\displaystyle [a;b]}$ .
Exemple : la fonction partie entière définie dans le cours sur les fonctions continues.
Si on la prend sur ${\displaystyle [0;3]}$ , alors ${\displaystyle (0;1;2;3)}$ est une subdivision adaptée à ${\displaystyle E}$ sur ${\displaystyle [0;3]}$ .${\displaystyle (0;2;3)}$ n'en est pas une car ${\displaystyle E}$ n’est pas constante sur ${\displaystyle [0;2]}$.

Définition : intégrale d'une fonction en escalier

Soit ${\displaystyle f\in {\mathcal {E}}([a;b])}$.
L'intégrale de la fonction ${\displaystyle f}$ sur ${\displaystyle [a;b]}$ est le nombre réel :

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\sum _{i=0}^{n-1}(a_{i+1}-a_{i})f(a_{i})}$

Exemple : pour la fonction partie entière, on a en choisissant la subdivision ${\displaystyle (0;1;2;3)}$ :
${\displaystyle \int _{0}^{3}E(x)\mathrm {d} x=\sum _{i=0}^{2}(a_{i+1}-a_{i})E(a_{i})=1+2=3}$ .

(manque d'illustrations)

Intégrale d'une fonction continue par morceaux

Définition : fonction continue par morceaux

Une fonction ${\displaystyle f:[a,b]\to \mathbb {R} }$ est dite continue par morceaux s'il existe une subdivision ${\displaystyle a=a_{1}<a_{2}<\cdots <a_{n}=b\;\;(n\in \mathbb {N} )}$ de ${\displaystyle [a,b]}$ telle que pour tout entier ${\displaystyle i}$ de ${\displaystyle 1}$ à ${\displaystyle n-1}$, ${\displaystyle f}$ soit continue sur ${\displaystyle ]a_{i},a_{i+1}[}$ et admette une limite à droite en ${\displaystyle a_{i}}$ et une limite à gauche en ${\displaystyle a_{i+1}}$.

Notation : dans cette leçon, nous noterons ${\displaystyle {\mathcal {CM}}([a,b])}$ l’ensemble des fonctions continues par morceaux sur ${\displaystyle [a,b]}$.

Propriété : approximation d'une fonction continue par morceaux par une fonction en escalier

Soit ${\displaystyle f\in {\mathcal {CM}}([a,b])}$.

${\displaystyle \forall \varepsilon >0\quad \exists \psi ,\varphi \in {\mathcal {E}}([a,b])\quad \psi \leq f\leq \varphi {\text{ et }}\varphi -\psi \leq \varepsilon }$.

Démonstration

On fait la preuve seulement pour ${\displaystyle f}$ continue : dans le cas général, on se place sur chacun des intervalles où la fonction est continue et on applique le résultat démontré ici.

${\displaystyle f}$ est continue sur l'intervalle fermé borné ${\displaystyle [a,b]}$ donc elle y est uniformément continue d’après le théorème de Heine. On a donc :

${\displaystyle \forall \varepsilon >0\quad \exists \delta >0\quad \forall x,y\in [a,b]\quad \left(|x-y|<\delta \Rightarrow |f(x)-f(y)|<\varepsilon \right)}$.

Soit ${\displaystyle \varepsilon >0}$ et soit ${\displaystyle (a_{1},a_{2},\dots ,a_{n})}$ une subdivision de ${\displaystyle [a,b]}$ telle que ${\displaystyle \forall i\in [1,n]\cap \mathbb {N} \quad a_{i+1}-a_{i}={\frac {b-a}{n}}<\delta }$.

On construit alors les fonctions ${\displaystyle \psi ,\varphi \in {\mathcal {E}}([a;b])}$ définies par :

• ${\displaystyle \psi (x)=m_{i}=\min _{x\in [a_{i},a_{i+1}]}f(x)}$ ;
• ${\displaystyle \varphi (x)=M_{i}=\max _{x\in [a_{i},a_{i+1}]}f(x)}$.

La continuité uniforme et la définition du minimum et du maximum (qui existent bien, puisque ${\displaystyle f}$ est continue sur l'intervalle fermé borné ${\displaystyle [a,b]}$) permettent alors de conclure.

 

Définition : fonction intégrable au sens de Riemann

On note :

• ${\displaystyle {\mathcal {E}}^{-}=\{\psi \in {\mathcal {E}}([a,b])\mid \psi \leq f\}}$ et ${\displaystyle {\mathcal {I}}^{-}=\left\{\int _{a}^{b}\psi (x)\mathrm {d} x\mid \psi \in {\mathcal {E}}^{-}\right\}}$
• ${\displaystyle {\mathcal {E}}^{+}=\{\varphi \in {\mathcal {E}}([a,b])\mid \varphi \geq f\}}$ et ${\displaystyle {\mathcal {I}}^{+}=\left\{\int _{a}^{b}\varphi (x)\mathrm {d} x\mid \varphi \in {\mathcal {E}}^{+}\right\}}$.

La fonction ${\displaystyle f}$ est dite intégrable au sens de Riemann si :

${\displaystyle {\mathcal {I}}:=\inf {\mathcal {I}}^{+}=\sup {\mathcal {I}}^{-}}$.

De plus, le nombre réel ${\displaystyle {\mathcal {I}}}$ est l'intégrale de la fonction ${\displaystyle f}$ sur ${\displaystyle [a,b]}$ :

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x={\mathcal {I}}}$.

Remarque : la variable d'intégration est « muette » : cela signifie que

${\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=\int _{a}^{b}f(t)\mathrm {d} t=\int _{a}^{b}f(u)\mathrm {d} u}$.

Théorème

Toute fonction continue par morceaux est Riemann-intégrable.

Remarque : En fait, l’ensemble des fonctions Riemann-intégrables est plus vaste que l’ensemble des fonctions continues par morceaux et on ne peut le décrire précisément.

Par exemple, la fonction ${\displaystyle f:x\mapsto {\begin{cases}0,&{\text{si }}x\in \mathbb {R} \setminus \mathbb {Q} \\{\frac {1}{q}},&{\text{si }}x={\frac {p}{q}}\mathrm {\;avec\;} p\mathrm {\;et\;} q\mathrm {\;premiers\;entre\;eux} \end{cases}}}$ est Riemann-intégrable sur ${\displaystyle \mathbb {R} }$, alors que la fonction ${\displaystyle g:x\mapsto {\begin{cases}0,&{\text{si }}x\in \mathbb {R} \setminus \mathbb {Q} \\1,&{\text{si }}x\in \mathbb {Q} \end{cases}}}$ n’est pas Riemann-intégrable.