Fonctions d'une variable réelle/Dérivabilité

Dérivabilité : définitions

Rappelons les définitions de la leçon « Fonction dérivée » :

Soit $f$ une fonction définie sur un intervalle $I$ , et soit $a\in I$ .

f

est dite dérivable en $a$ si son taux de variation entre $a$ et $x$ ,

{\frac {f(x)-f(a)}{x-a}}

, admet une limite finie quand

x

tend vers

a

.

Le réel $\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}$ est alors appelé nombre dérivé de $f$ en $a$ et est noté $f'(a)$ .

Si $f$ est dérivable en tous les points de $I$ , on dit que $f$ est dérivable sur $I$ .

On peut donner une définition équivalente (dont l'un des avantages est qu'elle se généralise au calcul différentiel à plusieurs variables) :

Proposition

Soit $f$ une fonction définie sur un intervalle $I$ , et soient $a\in I$ et $A\in \mathbb {R}$ .

La fonction $f$ est dérivable en $a$ et $f'(a)=A$ si, et seulement s'il existe une fonction $\varepsilon :I\to \mathbb {R}$ telle que :

$\lim _{x\to a}\varepsilon (x)=0\quad {\text{et}}\quad \forall x\in I\quad f(x)=f(a)+A(x-a)+\varepsilon (x)(x-a)\quad (\star )$ .

Remarque : L'expression $(\star )$ est un développement limité de $f$ au voisinage de $a$ à l’ordre 1 (c'est-à-dire une approximation affine de $f$ au voisinage de $a$ ).

Démonstration

Pour $x=a$ , l'équation $f(x)=f(a)+A(x-a)+\varepsilon (x)(x-a)$ est automatiquement vérifiée, quelle que soit la valeur de $\varepsilon (x)$ .

Pour $x\in I\setminus \{a\}$ , cette même équation équivaut à $\varepsilon (x)={\frac {f(x)-f(a)}{x-a}}-A$ .

L'existence d'une fonction $\varepsilon :I\to \mathbb {R}$ vérifiant la ligne $(\star )$ est donc équivalente à : $\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}-A=0$ , c'est-à-dire à : $\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}=A$ .

On a alors le lien avec la continuité :

Propriété

Si $f$ est dérivable en $a$ , alors $f$ est continue en $a$ .

La réciproque est fausse, comme le montre le contre-exemple ci-dessous de la fonction valeur absolue.

Démonstration

Le plus simple est d’utiliser la deuxième définition ci-dessus et de « passer à la limite » dans $(\star )$ .

On constate alors que $\lim _{x\to a}f(x)=f(a)$ , ce qui est la définition même de la continuité de $f$ en $a$ .

Le graphe de la fonction valeur absolue

x\mapsto |x|

a un point anguleux en 0.

Le graphe de la fonction racine carrée

x\mapsto {\sqrt {x}}

a une tangente verticale en 0.

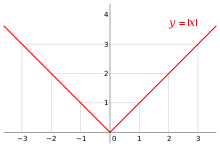
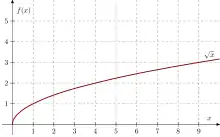
Parfois, en certains points, même si $f$ est continue en $a$ , elle n'y admet pas de nombre dérivé (cf. figures ci-contre).

En revanche, il existe parfois des « demi-tangentes » à droite et/ou à gauche. Cela conduit à des définitions de nombre dérivé « à gauche » ou « à droite ».

Définition

$f$ est dite dérivable en $a$ à droite si ${\frac {f(x)-f(a)}{x-a}}$ admet une limite finie quand $x$ tend vers $a$ par valeurs supérieures.
Le réel $\lim _{x\to a^{+}}{\frac {f(x)-f(a)}{x-a}}$ est alors appelé nombre dérivé à droite de $f$ en $a$ , et est noté $f'_{d}(a)$ .
$f$ est dite dérivable en $a$ à gauche si ${\frac {f(x)-f(a)}{x-a}}$ admet une limite finie quand $x$ tend vers $a$ par valeurs inférieures.
Le réel $\lim _{x\to a^{-}}{\frac {f(x)-f(a)}{x-a}}$ est alors appelé nombre dérivé à gauche de $f$ en $a$ , et est noté $f'_{g}(a)$ .

Propriété

Une fonction $f$ , définie sur un intervalle ouvert contenant $a$ , est dérivable en $a$ si et seulement si :

$f$ est dérivable en $a$ à droite et à gauche ;
$f'_{d}(a)=f'_{g}(a)$ .

Dans ce cas, $f'(a)=f'_{d}(a)=f'_{g}(a)$ .

Dérivée et opérations

Théorème

Soient $f$ et $g$ deux fonctions dérivables en $a\in I$ .

La dérivation au point $a$ $a$ est linéaire :
- $(f+g)'(a)=f'(a)+g'(a)$
- $\forall \lambda \in \mathbb {R} \quad (\lambda f)'(a)=\lambda (f'(a))$ .
$(fg)'(a)=f'(a)g(a)+f(a)g'(a)=(f'g+fg')(a)$
(et non pas $f'(a)g'(a)$ !).
si $g(a)\neq 0$ , alors $\left({\frac {f}{g}}\right)'(a)={\frac {f'(a)g(a)-f(a)g'(a)}{(g(a))^{2}}}$ et en particulier $\left({\frac {1}{g}}\right)'(a)={\frac {-g'(a)}{(g(a))^{2}}}$ .

Démonstrations

Toutes ces preuves utilisent les propriétés des opérations sur les limites et la définition de la dérivée comme limite du taux de variation.

Démonstration pour la somme
${\frac {(f+g)(x)-(f+g)(a)}{x-a}}={\frac {f(x)+g(x)-(f(a)+g(a)))}{x-a}}={\frac {f(x)-f(a)}{x-a}}+{\frac {g(x)-g(a)}{x-a}}$ .
Comme $\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}=f'(a)$ et $\lim _{a\to a}{\frac {g(x)-g(a)}{x-a}}=g'(a)$ , on a bien
$\lim _{x\to a}{\frac {(f+g)(x)-(f+g)(a)}{x-a}}=f'(a)+g'(a)$ , autrement dit : $(f+g)'(a)$ existe et est égale à $f'(a)+g'(a)$ .
Démonstration pour le produit
Le taux de variation de $fg$ au point $a$ s'écrit :
$T_{fg}(x,a)={\frac {f(x)g(x)-f(a)g(a)}{x-a}}.$
En retranchant et en ajoutant $f(a)g(x)$ on obtient alors :
$T_{fg}(x,a)={\frac {f(x)g(x)\overbrace {-f(a)g(x)+f(a)g(x)} ^{0}-f(a)g(a)}{x-a}}$ .
En factorisant les termes, on reconnaît les taux de variation de $f$ et $g$ :
$T_{fg}(x,a)=\underbrace {\frac {f(x)-f(a)}{x-a}} _{T_{f}(x,a)}g(x)+f(a)\underbrace {\frac {g(x)-g(a)}{x-a}} _{T_{g}(x,a)}.$
Sachant que $\lim _{x\to a}g(x)=g(a)$ (car $g$ est continue en $a$ , puisque dérivable en $a$ ), les règles sur les limites de produits et de sommes permettent de conclure :
${\bigl (}fg{\bigr )}'(a)=\lim _{x\to a}T_{fg}(x,a)=f'(a)g(a)+f(a)g'(a).$
Remarquons que le produit par une constante $\lambda$ est un cas particulier.
Démonstration pour l'inverse
On a successivement les égalités suivantes :
$\lim _{x\to a}{\frac {{\frac {1}{f}}(x)-{\frac {1}{f}}(a)}{x-a}}=\lim _{x\to a}{\frac {{\frac {1}{f(x)}}-{\frac {1}{f(a)}}}{x-a}}=\lim _{x\to a}{\frac {1}{f(x)f(a)}}{\frac {-(f(x)-f(a))}{x-a}}$
d'où le résultat grâce aux propriétés des limites.
Démonstration pour le quotient
Il suffit de combiner les deux points précédents (produit et inverse).

Dérivée d'une fonction composée

Soient $I$ et $J$ deux intervalles de $\mathbb {R}$ , $f:I\to \mathbb {R}$ et $g:J\to \mathbb {R}$ deux fonctions telles que $f(I)\subset J$ , et $a$ un point de $I$ .

Si $f$ est dérivable au point $a$ et $g$ est dérivable au point $f(a)$ alors la composée $g\circ f$ est dérivable au point $a$ et :

$(g\circ f)'(a)=(g'(f(a)))\times f'(a)$ .

Démonstration

Notons $b=f(a)$ . Puisque $g$ est dérivable en $b$ , d'après la seconde définition de la dérivabilité, il existe une fonction $u:J\to \mathbb {R}$ telle que

u(b)=\lim _{y\to b}u(y)=g'(b)\quad {\text{et}}\quad \forall y\in J\quad g(y)-g(b)=u(y)\times (y-b)

.

En particulier (en utilisant que $f$ est continue au point $a$ puisqu'elle est même dérivable en ce point) :

\lim _{x\to a}u(f(x))=g'(b)\quad {\text{et}}\quad \forall x\in I\quad g(f(x))-g(f(a))=u(f(x))\times (f(x)-f(a))

.

Le taux de variation au point $a$ de la fonction $g\circ f$ s'exprime alors sous la forme :

{\frac {g(f(x))-g(f(a))}{x-a}}=u(f(x))\times {\frac {f(x)-f(a)}{x-a}}

et quand $x$ tend vers $a$ (par valeurs distinctes de $a$ ), cette expression tend vers $g'(b)\times f'(a)=g'(f(a))\times f'(a)$ .

Remarque: Il existe une démonstration de ce théorème, apparemment plus simple, qui utilise l'« astuce »; ${\dfrac {g(f(x))-g(f(a))}{x-a}}={\dfrac {g(f(x))-g(f(a))}{f(x)-f(a)}}\times {\dfrac {f(x)-f(a)}{x-a}}$ ,; mais cette démonstration est erronée car elle suppose que $f(x)\neq f(a)$ pour tout $x$ suffisamment proche de $a$ , ce qui n'a aucune raison d’être.

Exemples : Remarquez que dans ces exemples, on utilise le formulaire du paragraphe suivant.

Calculer la dérivée de la fonction ${\displaystyle \varphi$ .
On pose $\varphi (x)=f(x)+g(x)$ où $f(x)={\frac {1}{x^{2}}}\Rightarrow f'(x)=-{\frac {2}{x^{3}}}$ et $g(x)=\ln x\Rightarrow g'(x)={\frac {1}{x}}$ .
Donc : $\varphi '(x)=f'(x)+g'(x)=-{\frac {2}{x^{3}}}+{\frac {1}{x}}={\frac {x^{2}-2}{x^{3}}}$ .
Calculer la dérivée de la fonction ${\displaystyle \varphi$ .
On pose $\varphi (x)=f(x)g(x)$ où $f(x)=x^{2}\Rightarrow f'(x)=2x$ et $g(x)=g'(x)=\mathrm {e} ^{x}$ .
Donc : $\varphi '(x)=f'(x)g(x)+f(x)g'(x)=2x\mathrm {e} ^{x}+x^{2}\mathrm {e} ^{x}=(x^{2}+2x)\mathrm {e} ^{x}$ .
Calculer la dérivée de la fonction ${\displaystyle \varphi$ .
On pose $\varphi (x)={\frac {f}{g}}(x)$ où $f(x)=\cos x\Rightarrow f'(x)=-\sin x$ et $g(x)={\sqrt {x}}\Rightarrow g'(x)={\frac {1}{2{\sqrt {x}}}}$ .
Donc : $\varphi '(x)={\frac {f'(x)g(x)-f(x)g'(x)}{(g(x))^{2}}}={\frac {-{\sqrt {x}}\sin x-\cos x\times {\frac {1}{2{\sqrt {x}}}}}{({\sqrt {x}})^{2}}}=-{\frac {2x\sin x+\cos x}{2x{\sqrt {x}}}}$ .
Calculer la dérivée d'une fonction de la forme ${\displaystyle \varphi$ .
On a $\varphi =\exp \circ f$ et $\exp '=\exp$ ,
donc $\varphi '(x)=f'(x)\exp '(f(x))$ , c'est-à-dire : $\left(\mathrm {e} ^{f}\right)'=f'\times \mathrm {e} ^{f}$ .

Dérivée d'une bijection réciproque

Soient $I$ un intervalle réel et $f:I\to \mathbb {R}$ une fonction dérivable sur $I$ et strictement monotone ( $f$ est alors une bijection de $I$ sur l'intervalle $f(I)$ ).

Pour tout point $a$ de $I$ en lequel $f'$ ne s'annule pas, la bijection réciproque $f^{-1}$ est dérivable en $b:=f(a)$ et :

$(f^{-1})'(b)={\frac {1}{f'(a)}}$ .

Par conséquent, si $f'$ ne s'annule pas sur $I$ , alors $f^{-1}$ est dérivable sur $f(I)$ et $(f^{-1})'={\frac {1}{f'\circ f^{-1}}}$ .

Démonstration

D'après le théorème de la bijection, l'application $g:=f^{-1}$ est continue en $b$ et même (par injectivité de $g$ ) quand $y$ tend vers $b$ par valeurs distinctes de $b$ , $g(y)$ tend vers $g(b)=a$ par valeurs distinctes de $a$ .
Par hypothèse, $\lim _{\stackrel {x\to a}{x\neq a}}{\frac {f(x)-f(a)}{x-a}}=f'(a)$ .

Par composition des limites, on déduit de ces deux points que

\lim _{\stackrel {y\to b}{y\neq b}}{\frac {f(g(y))-f(a)}{g(y)-a}}=f'(a)

,

ou encore :

\lim _{\stackrel {y\to b}{y\neq b}}{\frac {y-b}{g(y)-g(b)}}=f'(a)

.

Cette limite étant non nulle, on a donc bien (d'après le théorème sur la limite de l'inverse) :

\lim _{\stackrel {y\to b}{y\neq b}}{\frac {g(y)-g(b)}{y-b}}={\frac {1}{f'(a)}}

, c'est-à-dire

g'(b)={\frac {1}{f'(a)}}

.

Remarques.

Si $f'(a)=0$ , le même calcul montre que $\lim _{\stackrel {y\to b}{y\neq b}}\left|{\frac {g(y)-g(b)}{y-b}}\right|=+\infty$ donc $g$ n'est pas dérivable en $b$ .
Le point crucial dans cette démonstration était la preuve que $g$ est dérivable en $b$ . Si l'on admet ce fait, la formule $g'(b)={\frac {1}{f'(a)}}$ peut se retrouver en appliquant propriété précédente (« Dérivée d'une fonction composée ») : $g'(b)f'(a)=g'(f(a))f'(a)=(g\circ f)'(a)=\mathrm {id} '(a)=1$ .

Dérivée des fonctions usuelles

Domaine de définition $D_{f}$	Fonction $f(x)$	Domaine de dérivabilité $D_{f'}$	Dérivée $f'(x)$	Condition
$\mathbb {R}$	$ax+b$	$\mathbb {R}$	$a$	$a,b\in \mathbb {R}$
$\mathbb {R}$	$x^{n}$	$\mathbb {R}$	$nx^{n-1}$	$n\in \mathbb {N}$
$\mathbb {R} ^{*}$	${\frac {1}{x^{n}}}$	$\mathbb {R} ^{*}$	$-{\frac {n}{x^{n+1}}}$	$n\in \mathbb {N} ^{*}$
$\mathbb {R} _{+}^{*}$ (ou $\mathbb {R} _{+}$ si $\alpha >0$ )	$x^{\alpha }$	$\mathbb {R} _{+}^{*}$ (ou $\mathbb {R} _{+}$ si $\alpha >1$ )	$\alpha x^{\alpha -1}$	$\alpha \in \mathbb {R} \setminus \mathbb {Z}$
$\mathbb {R}$	$\sin x$	$\mathbb {R}$	$\cos x$
$\mathbb {R}$	$\cos x$	$\mathbb {R}$	$-\sin x$
$\mathbb {R} \setminus \left({\frac {\pi }{2}}+\pi \mathbb {Z} \right)$	$\tan x$	$\mathbb {R} \setminus \left({\frac {\pi }{2}}+\pi \mathbb {Z} \right)$	${\frac {1}{\cos ^{2}x}}=1+\tan ^{2}x$
$\mathbb {R} \setminus \left(\pi \mathbb {Z} \right)$	$\cot x$	$\mathbb {R} \setminus \left(\pi \mathbb {Z} \right)$	$-{\frac {1}{\sin ^{2}x}}=-1-\cot ^{2}x$
$\left[-1,1\right]$	$\arcsin x$	$\left]-1,1\right[$	${\frac {1}{\sqrt {1-x^{2}}}}$
$\left[-1,1\right]$	$\arccos x$	$\left]-1,1\right[$	$-{\frac {1}{\sqrt {1-x^{2}}}}$
$\mathbb {R}$	$arctan$ $x$	$\mathbb {R}$	${\frac {1}{1+x^{2}}}$
$\mathbb {R} _{+}^{*}$	$\log _{a}x$	$\mathbb {R} _{+}^{*}$	${\frac {1}{x\ln a}}$	$a>0$
$\mathbb {R}$	$a^{x}$	$\mathbb {R}$	$a^{x}\ln a$	$a>0$
$\mathbb {R}$	$\operatorname {sh} x$	$\mathbb {R}$	$\operatorname {ch} x$
$\mathbb {R}$	$\operatorname {ch} x$	$\mathbb {R}$	$\operatorname {sh} x$
$\mathbb {R}$	$\operatorname {th} x$	$\mathbb {R}$	${\frac {1}{\operatorname {ch} ^{2}x}}$
$\mathbb {R}$	$\operatorname {argsh} x$	$\mathbb {R}$	${\frac {1}{\sqrt {1+x^{2}}}}$
$\left[1,+\infty \right[$	$\operatorname {argch} x$	$\left]1,+\infty \right[$	${\frac {1}{\sqrt {x^{2}-1}}}$
$\left]-1,1\right[$	$\operatorname {argth} x$	$\left]-1,1\right[$	${\frac {1}{1-x^{2}}}$

Il faut être capable de démontrer ces résultats : deux de ces démonstrations sont proposées dans les deux boîtes déroulantes ci-dessous. On en trouve d'autres dans le chapitre « Dérivées usuelles » de la leçon « Fonction dérivée ».

Dérivée de x ↦ xⁿ

On démontre le résultat pour $f:x\mapsto x^{n}$ où $n\in \mathbb {N} ^{*}$ . Pour tout $a\in \mathbb {R}$ :

$\forall x\neq a\quad {\frac {f(x)-f(a)}{x-a}}={\frac {x^{n}-a^{n}}{x-a}}={\frac {(x-a)(x^{n-1}+ax^{n-2}+a^{2}x^{n-3}+\cdots +a^{n-1})}{x-a}}=x^{n-1}+ax^{n-2}+a^{2}x^{n-3}+\cdots +a^{n-1}$ et

$\lim _{x\to a}(x^{n-1}+ax^{n-2}+a^{2}x^{n-3}+\cdots +a^{n-1})=na^{n-1}$ (car chaque terme est de la forme $a^{k}x^{n-1-k}$ et il y a $n-1$ termes)

donc $\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}=na^{n-1}$ , ce qui est le résultat voulu.

Dérivée de x ↦ x^α

Soit $h(x)=x^{\alpha }$ , défini pour $x>0$ par :

h(x)=\mathrm {e} ^{f(x)}

avec

f(x)=\alpha \ln x

.

D'après l'exemple 4 ci-dessus, pour tout $x>0$ : $h'(x)=\mathrm {e} ^{f(x)}f'(x)=x^{\alpha }{\frac {\alpha }{x}}=\alpha x^{\alpha -1}$ .

Théorèmes sur la dérivation

Voici une condition nécessaire mais pas suffisante pour un extremum local.

Théorème de Fermat

Soit $f$ une fonction définie sur un intervalle ouvert $\left]a,b\right[$ et dérivable en un point $c\in \left]a,b\right[$ .

Si $f$ possède un extremum local en $c$ , alors $f'(c)=0$ .

Attention

La réciproque est fausse : par exemple, la fonction $\mathbb {R} \to \mathbb {R} ,\,x\mapsto x^{3}$ , en $0$ , a une dérivée nulle mais pas d'extremum local.
L'hypothèse « intervalle ouvert » (ou encore : $c$ n'est pas une borne de l'intervalle) est nécessaire. Par exemple, la fonction $f:[0,1]\to \mathbb {R} ,\,x\mapsto x$ admet un minimum en $0$ et un maximum en $1$ , mais sa dérivée ne s'annule en aucun point.

Démonstration

On suppose ici que $f(c)$ est un maximum local.

Il existe donc un réel $r>0$ tel que $\left]c-r,c+r\right[\subset I$ et tel que $\forall x\in \left]c-r,c+r\right[\quad f(x)\leq f(c)$ , ou encore : $\forall h\in \left]-r,r\right[\quad f(c+h)-f(c)\leq 0$ .

Pour $0<h<r$ , on a ${\frac {f(c+h)-f(c)}{h}}\leq 0$ . En considérant la limite quand $h$ tend vers $0$ par valeurs positives, on en déduit : $f'(c)\leq 0$ .
Pour $-r<h<0$ , on a ${\frac {f(c+h)-f(c)}{h}}\geq 0$ . En considérant la limite quand $h$ tend vers $0$ par valeurs négatives, on en déduit : $f'(c)\geq 0$ .

Finalement, $f'(c)\leq 0$ et $f'(c)\geq 0$ donc $f'(c)=0$ .

Le cas où $f(c)$ est un minimum local se démontre de la même manière (avec la seule différence que les signes des taux de variation sont intervertis), ou se déduit du cas ci-dessus (en considérant la fonction $-f$ ).

C'est parce que $c$ appartient à l'intervalle ouvert $\left]a,b\right[$ que l'on a pu considérer ces deux taux de variation : si $c$ était une borne de l'intervalle, l'un des deux ne serait pas défini.

Théorème de Rolle

Soit $f$ une fonction continue sur $\left[a,b\right]$ et dérivable sur $\left]a,b\right[$ telle que $f(a)=f(b)$ .

Alors, il existe au moins un réel $c\in \left]a,b\right[$ tel que $f'(c)=0$ .

Le théorème de Rolle permet d'affirmer qu’il existe au moins un réel

c\in \left]a,b\right[

tel que la tangente à la courbe de

f

au point

(c,f(c))

soit « horizontale ».

Démonstration

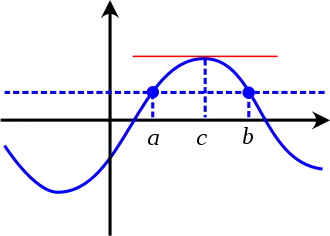
Si $f$ est constante alors sa dérivée est nulle sur $\left]a,b\right[$ , et l’on peut prendre pour $c$ n'importe quel point de cet intervalle.

Supposons maintenant que $f$ prend au moins une valeur différente du nombre $f(a)=f(b)$ , par exemple une valeur strictement supérieure à ce nombre. Puisque $f$ est continue sur l'intervalle fermé borné $\left[a,b\right]$ , elle admet et atteint (d'après le théorème des bornes) un maximum global en un certain $c\in \left[a,b\right]$ . Ce maximum $f(c)$ étant strictement supérieur au nombre $f(a)=f(b)$ , le point $c$ est différent de $a$ et de $b$ donc il appartient à l'intervalle ouvert $\left]a,b\right[$ . Le théorème de Fermat ci-dessus permet de conclure : $f(c)$ est un extremum local de $f$ donc $f'(c)=0$ .

Théorème des accroissements finis

Théorème des accroissements finis : Soit $f$ $f$ une fonction continue sur $\left[a,b\right]$ $\left[a,b\right]$ et dérivable sur $\left]a,b\right[$ $\left]a,b\right[$ . Alors,
- il existe au moins un réel $c\in \left]a,b\right[$ tel que $f'(c)={\frac {f(b)-f(a)}{b-a}}$ .
Théorème des accroissements finis généralisé : soient $f$ $f$ et $g$ $g$ deux fonctions continues sur $\left[a,b\right]$ $\left[a,b\right]$ et dérivables sur $\left]a,b\right[$ $\left]a,b\right[$ . Alors :
- il existe au moins un réel $c\in \left]a,b\right[$ tel que $\left(g(b)-g(a)\right)f'(c)=\left(f(b)-f(a)\right)g'(c)$ ;
- dans le cas où $g'$ ne s'annule pas sur $\left]a,b\right[$ , l'égalité peut s'écrire : ${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}$ (« théorème de la moyenne de Cauchy »).

Graphiquement, le théorème des accroissements finis s'interprète en disant qu’il existe, sur la courbe de

f

, au moins un point

(c,f(c))

, strictement compris entre les extrémités

(a,f(a))

et

(b,f(b))

, et en lequel la tangente est parallèle à la corde reliant ces extrémités.

Démonstration

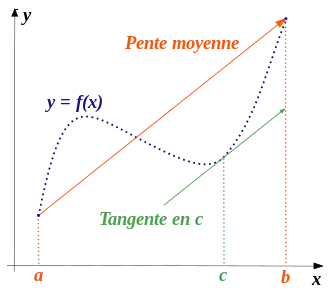
Le point 1 s'obtient en appliquant le théorème de Rolle à la fonction auxiliaire $t\mapsto f(t)-{\frac {f(b)-f(a)}{b-a}}\ t$ , ou comme cas particulier $g(t)=t$ du point 2.
On généralise l'idée précédente en appliquant le théorème de Rolle à la fonction ${\displaystyle \varphi$ :\left[a,b\right]\to \mathbb {R} ,\ t\mapsto \left(g(b)-g(a)\right)f(t)-\left(f(b)-f(a\right))g(t)} $\varphi :\left[a,b\right]\to \mathbb {R} ,\ t\mapsto \left(g(b)-g(a)\right)f(t)-\left(f(b)-f(a\right))g(t)$ . Cette fonction est bien continue sur $\left[a,b\right]$ $\left[a,b\right]$ et dérivable sur $\left]a,b\right[$ $\left]a,b\right[$ , et $\varphi (a)=\varphi (b)$ $\varphi (a)=\varphi (b)$ .
- Il existe donc un réel $c\in \left]a,b\right[$ tel que $\varphi '(c)=0$ , ce qui donne l'égalité annoncée.
- Si de plus $g'$ ne s'annule pas sur $\left]a,b\right[$ alors $g(b)\neq g(a)$ (par contraposée du théorème de Rolle) et l'on peut diviser les deux membres de l'égalité précédente par $\left(g(b)-g(a)\right)g'(c)$ .

Ce théorème a quatre corollaires importants : l'inégalité des accroissements finis, le théorème « limite de la dérivée », la règle de l'Hôpital et, surtout, le lien entre sens de variation d'une fonction et signe de sa dérivée.

Inégalité des accroissements finis

Soient $f$ une fonction continue sur $\left[a,b\right]$ et dérivable sur $\left]a,b\right[$ , et $M$ un réel tel que $\forall t\in \left]a,b\right[\quad |f'(t)|\leq M$ . Alors :

|f(b)-f(a)|\leq M|b-a|

.

Démonstration

Il suffit d'appliquer le théorème des accroissements finis et de majorer $|f'(c)|$ par $M$ .

Signalons que pour les fonctions à valeurs vectorielles, on ne dispose pas d'un théorème des accroissements finis, mais on parvient à démontrer, d'une autre manière, cette inégalité fort utile : voir la leçon « Calcul différentiel ».

On verra une application de cette inégalité, à propos des fonctions lipschitziennes, au chapitre « Continuité uniforme ».

Voici enfin un théorème bien pratique pour calculer un nombre dérivé :

Théorème « limite de la dérivée »

Soit $f$ une fonction continue sur un intervalle $I$ ( $a\in I$ ) et dérivable sur $I\setminus \{a\}$ .

Si $\lim _{x\to a}f'(x)=l\in \mathbb {R}$ , alors $f$ est dérivable en $a$ et $f'(a)=l$ .

Démonstration

Il suffit d'appliquer le théorème des accroissements finis à la fonction $f$ sur les deux intervalles $J_{1}$ et $J_{2}$ tels que $J_{1}\cup J_{2}\cup \{a\}=I$ : $\forall x\in J_{1}\quad \exists c_{x}\in J_{1}\quad f'(c_{x})={\frac {f(x)-f(a)}{x-a}}$ (et de même sur $J_{2}$ ).

Alors $\lim _{x\to a}f'(c_{x})=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}=l$ donc, par définition, $f'(a)=l$ .

L'énoncé suivant généralise la « règle simple de L'Hôpital » (qui n'est qu'une application directe de la définition d'un nombre dérivé). Il s'applique à des fonctions définies et dérivables à droite (ou à gauche) d'un point $a\in {\overline {\mathbb {R} }}$ (c'est-à-dire réel ou infini), mais pas en ce point :

Règles de L'Hôpital

Soient $f$ et $g$ deux fonctions dérivables sur $\left]a,b\right[$ et telles que $g'$ ne s'annule pas.

Si $\lim _{a}f=\lim _{a}g=0$ et $\lim _{a^{+}}{\frac {f'}{g'}}=\ell \in {\overline {\mathbb {R} }}$ alors $\lim _{a^{+}}{\frac {f}{g}}=\ell$ .
Si $\lim _{a}|g|=+\infty$ et si $\lim _{a^{+}}{\frac {f'}{g'}}=\ell \in {\overline {\mathbb {R} }}$ alors $\lim _{a^{+}}{\frac {f}{g}}=\ell$ .

Démonstration

Pour tout réel $x$ de $\left]a,b\right[$ , on applique le « théorème de la moyenne de Cauchy » (cf. théorème des accroissements finis ci-dessus) à $f$ et $g$ entre $a$ et $x$ . On obtient ainsi un réel $c_{x}$ de $\left]a,x\right[$ tel que
${\frac {f(x)}{g(x)}}={\frac {f'(c_{x})}{g'(c_{x})}}$ .
Puisque
$\lim _{x\to a^{+}}c_{x}=a,~c_{x}>a{\text{ et }}\lim _{c\to a^{+}}{\frac {f'(c)}{g'(c)}}=\ell$ ,
on obtient
$\lim _{x\to a^{+}}{\frac {f(x)}{g(x)}}=\ell$ .
On utilise le même théorème de la moyenne de Cauchy, avec plus de précaution.
Dans tout intervalle non vide $\left]x,y\right[$ inclus dans $\left]a,b\right[$ , il existe un réel $c$ tel que ${\frac {f(x)-f(y)}{g(x)-g(y)}}={\frac {f'(c)}{g'(c)}}$ , autrement dit $f(x)=(g(x)-g(y)){\frac {f'(c)}{g'(c)}}+f(y)$ .
Lorsque $g(x)$ est non nul, l'expression précédente peut s'écrire :
${\frac {f(x)}{g(x)}}=\left(1-{\frac {g(y)}{g(x)}}\right){\frac {f'(c)}{g'(c)}}+{\frac {f(y)}{g(x)}}$ .
Comme $\lim _{t\to a^{+}}{\frac {f'(t)}{g'(t)}}=\ell$ , on peut choisir $y$ dans $\left]a,b\right[$ tel que, si $c$ appartient à $\left]a,y\right[$ , ${\frac {f'(c)}{g'(c)}}$ soit aussi proche que l'on veut de $\ell$ .
Puis, pour un tel $y$ , comme $|g(x)|$ tend vers l'infini, on peut trouver un intervalle non vide $\left]a,r\right[$ , inclus dans $\left]a,y\right[$ , tel que pour tout $x$ de $\left]a,r\right[$ , $g(x)$ soit non nul et ${\frac {g(y)}{g(x)}}$ et ${\frac {f(y)}{g(x)}}$ soient aussi proches de $0$ que l'on veut.

Remarques

Ces règles peuvent être itérées $n$ fois (pour un entier $n>0$ ) : on dit alors qu'on applique la règle de L'Hôpital « à l’ordre $n$ ».
La première de ces deux règles sera utilisée pour démontrer le théorème d'intégration terme à terme d'un développement limité, qui permet d'établir une formule fondamentale : la formule de Taylor-Young.

Dérivée et sens de variation

La propriété qui suit fournit un critère pour le sens de variation d'une fonction dérivable :

Propriété

Soient $I$ un intervalle réel et $f:I\to \mathbb {R}$ une fonction dérivable.

$f$ est croissante si et seulement si $f'\geq 0$ .
$f$ est décroissante si et seulement si $f'\leq 0$ .
$f$ est constante si et seulement si $f'=0$ .
Si $f'>0$ (resp. $<0$ ) alors $f$ est strictement croissante (resp. strictement décroissante).

Démonstration

Supposons $f$ croissante. Alors, tous les taux de variation de $f$ sont positifs :
$\forall x\in I\quad \forall y\in I\setminus \{x\}\quad {\frac {f(y)-f(x)}{y-x}}\geq 0$ .
Par passage à la limite dans les inégalités, tous les nombres dérivés de $f$ le sont donc aussi :
$\forall x\in I\quad f'(x)=\lim _{y\to x}{\frac {f(y)-f(x)}{y-x}}\geq 0$ .
Réciproquement, supposons que $\forall x\in I\quad f'(x)\geq 0$ . Soient $x,y\in I$ tels que $x<y$ .
Le théorème des accroissements finis (voir supra) assure qu’il existe $c\in \left]x,y\right[$ tel que ${\frac {f(x)-f(y)}{x-y}}=f'(c)$ .
Comme $f'(c)\geq 0$ (par hypothèse) et $y-x>0$ , on en déduit que $f(y)-f(x)\geq 0$ .
On a donc bien : $\forall x,y\in I\quad x<y\Rightarrow f(x)\leq f(y)$ , c'est-à-dire que $f$ est croissante.
La caractérisation de la décroissance de $f$ se démontre de même, ou se déduit de celle de la croissance de $-f$ .
$f$ est constante si et seulement si elle est à la fois croissante et décroissante.
La condition suffisante de monotonie stricte se démontre de la même façon que celle de monotonie.

Pour des exemples, voir le chapitre « Dérivée et sens de variation » et ses exercices, dans la leçon « Étude et tracé d'une fonction ».

Classes de régularité et dérivées d'ordre supérieur

Soit $I$ un intervalle de $\mathbb {R}$ .

Dérivées d'ordre supérieur

Définition

Soit $f$ une fonction dérivable sur $I$ . Les dérivées successives de $f$ , si elles existent, sont définies par récurrence de la façon suivante :

$f^{(0)}=f$ ;
$f^{(n+1)}=(f^{(n)})'\,\forall n\in \mathbb {N}$ .

(exemple à faire)

Attention à ne pas confondre la dérivée n-ième $f^{(n)}$ avec la puissance n-ième $f^{n}$ .

Propriété

Soient $f$ et $g$ deux fonctions dérivables $n$ fois ( $n\in \mathbb {N}$ ).

On a :

$(f+g)^{(n)}=f^{(n)}+g^{(n)}$ ;
$\forall \lambda \in \mathbb {R} \quad (\lambda f)^{(n)}=\lambda f^{(n)}$ .

Cette propriété se démontre par récurrence sur $n$ en utilisant la linéarité de la dérivation.

Pour le produit, on voit apparaître des coefficients binomiaux :

Formule de Leibniz

Si $f$ et $g$ sont $n$ fois dérivables en un point $x\in \mathbb {R}$ ( $n\in \mathbb {N}$ ), alors leur produit l'est aussi et

$(fg)^{(n)}(x)=\sum _{k=0}^{n}{\binom {n}{k}}f^{(k)}(x)g^{(n-k)}(x)$ .

Cette formule a la même forme et se démontre de la même façon que la formule du binôme.

Démonstration

Pour n = 0 on a bien :

(fg)^{(0)}(x)=f(x)g(x)={0 \choose 0}f^{(0)}(x)g^{(0)}(x)

.

Pour n entier supérieur ou égal à 1, nous démontrerons la formule de Leibniz par récurrence. (On a traité à part le cas n = 0 car, sinon, au cours de la démonstration ci-dessous, il apparaîtrait des sommes de la forme $\sum _{i=1}^{0}\dots$ , qui n'auraient pas de sens.)

Pour $n=1$ , la formule est vraie d'après la règle du produit :

(fg)'(x)=f'(x)g(x)+f(x)g'(x)=\sum _{k=0}^{1}{\binom {1}{k}}\ f^{(1-k)}(x)g^{(k)}(x)

.

Nous devons maintenant montrer que pour tout entier $k$ supérieur ou égal à 1, si la formule est vraie pour $n=k$ , alors elle est aussi vraie pour $n=k+1$ .

Au voisinage de $x$ , on a par hypothèse :

(fg)^{(k)}=\sum _{i=0}^{k}{\binom {k}{i}}f^{(k-i)}g^{(i)}.

Si l'on dérive au point $x$ cette expression, on obtient par la règle du produit :

(fg)^{(k+1)}(x)=\sum _{i=0}^{k}{\binom {k}{i}}f^{(k+1-i)}(x)g^{(i)}(x)+\sum _{i=0}^{k}{\binom {k}{i}}f^{(k-i)}(x)g^{(i+1)}(x).

Par changement d'indice $j=i+1$ , cette expression se réécrit :

{\begin{aligned}(fg)^{(k+1)}(x)&=\sum _{i=0}^{k}{\binom {k}{i}}f^{(k+1-i)}(x)g^{(i)}(x)+\sum _{j=1}^{k+1}{\binom {k}{j-1}}f^{(k+1-j)}(x)g^{(j)}(x)\\&={\binom {k}{0}}f^{(k+1)}(x)g^{(0)}(x)+\left[\sum _{i=1}^{k}{\binom {k}{i}}f^{(k+1-i)}(x)g^{(i)}(x)\right]+\left[\sum _{j=1}^{k}{\binom {k}{j-1}}f^{(k+1-j)}(x)g^{(j)}(x)\right]+{\binom {k}{k}}f^{(0)}(x)g^{(k+1)}(x)\\&=f^{(k+1)}(x)g^{(0)}(x)+\left[\sum _{i=1}^{k}\left({\binom {k}{i}}+{\binom {k}{i-1}}\right)f^{(k+1-i)}(x)g^{(i)}(x)\right]+f^{(0)}(x)g^{(k+1)}(x).\end{aligned}}

On conclut en utilisant la formule de Pascal :

{\begin{aligned}(fg)^{(k+1)}(x)&=f^{(k+1)}(x)g^{(0)}(x)+\left[\sum _{i=1}^{k}{\binom {k+1}{i}}f^{(k+1-i)}(x)g^{(i)}(x)\right]+f^{(0)}(x)g^{(k+1)}(x)\\&=\sum _{i=0}^{k+1}{\binom {k+1}{i}}f^{(k+1-i)}(x)g^{(i)}(x).\end{aligned}}

La règle est donc aussi vraie pour $n=k+1$ . Par récurrence, la règle est donc vraie pour tout entier $n$ supérieur ou égal à 1.

Note : on peut aussi démontrer la formule de Leibniz en utilisant un développement de Taylor-Young.

Exemple

Avec n = 2 on a :

\displaystyle (fg)''=f''g+2f'g'+fg''

,

soit, pour trouver la dérivée seconde de $x\mapsto (x^{2}+1)\sin(x)$ :

\left[(x^{2}+1)\sin(x)\right]''=2\sin(x)+4x\cos(x)-(x^{2}+1)\sin(x)

.

Enfin, on a la propriété suivante qui se généralisera en calcul différentiel :

Propriété

Soit $f$ une fonction 2 fois dérivable sur $I$ et $a\in I$ tel que $f'(a)=0$ .

Si $\forall x\in I,f''(x)>0$ , alors $f(a)$ est un minimum local de $f$ sur $I$ .
Si $\forall x\in I,f''(x)<0$ , alors $f(a)$ est un maximum local de $f$ sur $I$ .

Démonstration

On ne démontre que la première assertion :

$f''(x)>0\forall x\in I\Rightarrow f'\mathrm {croissante\,\,sur\,\,} I$ , et donc comme $f'(a)=0$

$f'(x)<0\forall x\in I,x<a$ et $f'(x)>0\forall x\in I,x>a$ . On en déduit que $f$ est décroissante « à gauche de $a$ » et croissante « à droite de $a$ », ce qui montre que $f(a)$ est un minimum local.

Classes de régularité

Définition

Soit $n\in \mathbb {N}$ . On dit qu'une fonction $f$ est de classe ${\mathcal {C}}^{n}$ sur $I$ , et l'on note $f\in C^{n}(I)$ , si :

$f$ est $n$ fois dérivable sur $I$ ;
sa dérivée $n$ -ième (c'est-à-dire la fonction $f^{(n)}$ ) est continue sur $I$ .

Donc $f\in C^{0}(I)$ signifie simplement que $f$ est continue sur $I$ .

On peut aussi parler de la classe $C^{\infty }(\mathbb {R} )$ , avec les polynômes, l'exponentielle, le sinus, le cosinus et la gaussienne $x\mapsto \mathrm {e} ^{-ax^{2}}$ ( $a\in \mathbb {R} _{+}^{*}$ ) :

Définition

Une fonction $f$ est dite de classe ${\mathcal {C}}^{\infty }$ sur $I$ si elle est $n$ fois dérivable sur $I$ pour tout $n\in \mathbb {N}$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.