Fonction dérivée/Nombre dérivé

Accroissement d'une fonction affine

Soit une fonction affine ƒ définie sur $\mathbb {R}$ par $f:x\mapsto ax+b$ .

a est appelé le coefficient directeur de ƒ.

Pour déterminer ce coefficient directeur à partir de la représentation graphique de la fonction,

on choisit deux points du graphe et on mesure (cf. figure ci-contre) :

la différence des abscisses Δx
la différence des ordonnées Δy

On a alors $a={\frac {\Delta y}{\Delta x}}$

La grandeur a caractérise la pente de la droite :

plus a est grand et plus la droite monte vite.

On appelle donc également a accroissement de la fonction ƒ.

Accroissement moyen

Introduction

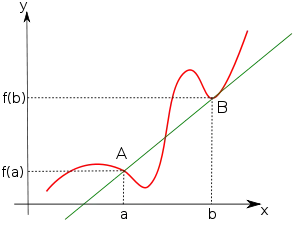
Dans le cas d'une fonction $f:x\mapsto f(x)$ quelconque, définie sur un intervalle I, (voir figure ci-contre), l'accroissement de la fonction n’est pas constant. Parfois la fonction monte, parfois elle redescend, plus ou moins vite. On ne peut pas travailler aussi simplement qu'avec les fonctions affines.

On introduit donc la notion d'accroissement moyen sur un intervalle.

Définition

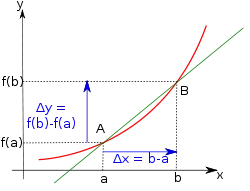
Soient $a\in I,~b\in I$ .

On note A et B les points de la courbe représentative de ƒ dans un repère $(O;{\vec {i}},{\vec {j}})$ qui ont pour abscisses respectives a et b:

$A(a;f(a))$
$B(b;f(b))$

La droite $(AB)$ est une corde de la courbe $y=f(x)$ ,

Son coefficient directeur vaut : ${\frac {\Delta y}{\Delta x}}={\frac {\Delta (f(x))}{\Delta x}}={\frac {f(b)-f(a)}{b-a}}$ et s’appelle accroissement moyen de ƒ entre a et b

Voyons sur quelques exemples l'utilité de l'accroissement moyen d'une fonction entre deux points.

Exemple 1

Un véhicule parcourt 1 000 km en 10 h. Quelle est sa vitesse moyenne ?

$V_{m}=\dots$

Solution

Pour avoir le résultat, il suffit de diviser la distance qui a été parcourue (ici 1 000 km) entre l'instant de départ et l'instant d'arrivée (ici espacés de 10 heures)

${\begin{array}{|c|c|}{\textrm {Exemple}}&{\textrm {Equivalent~dans~l'introduction}}\\\hline {\rm {Temps}}&{\rm {Variable}}~x\\10~{\rm {h}}&b-a\\\hline {\rm {Distance}}&{\rm {Fonction}}~f\\1000~{\rm {km}}&f(b)-f(a)\\\hline {\rm {Vitesse~moyenne~}}V_{m}&\displaystyle {\frac {f(b)-f(a)}{b-a}}\\\hline \end{array}}$

$V_{m}={\frac {1000~{\rm {km}}}{10~{\rm {h}}}}=100~{\rm {km.h}}^{-1}$

La vitesse moyenne est l'accroissement moyen de la fonction qui donne la distance parcourue en fonction du temps entre le départ et l'arrivée.

Exemple 2

Un pays produit annuellement 1 000 t de blé en l'an 1900 et 10 000 t de blé en l'an 2000. De combien de tonnes la production a-t-elle augmenté en moyenne par an ?

Solution

${\begin{array}{|c|c|}{\textrm {Exemple}}&{\textrm {Equivalent~dans~l'introduction}}\\\hline {\rm {Date}}&{\rm {Variable}}~x\\1900&a\\2000&b\\\hline {\rm {Production}}&{\rm {Fonction}}~f\\1000~{\rm {t}}&f(a)\\10000~{\rm {t}}&f(b)\\\hline {\rm {Augmentation~moyenne~de~production}}&\displaystyle {\frac {f(b)-f(a)}{b-a}}\\\hline \end{array}}$

On a donc une augmentation annuelle moyenne de ${\frac {f(b)-f(a)}{b-a}}={\frac {9000~{\rm {t}}}{100~{\rm {ans}}}}=90{\rm {t/an}}$

Nombre dérivé d'une fonction en x = a

Introduction

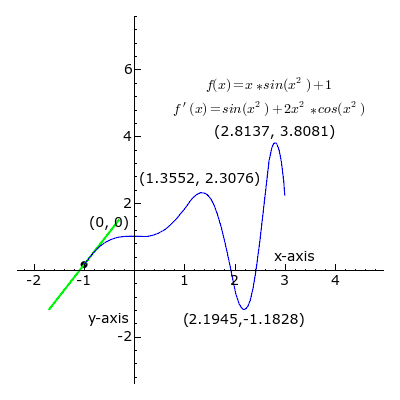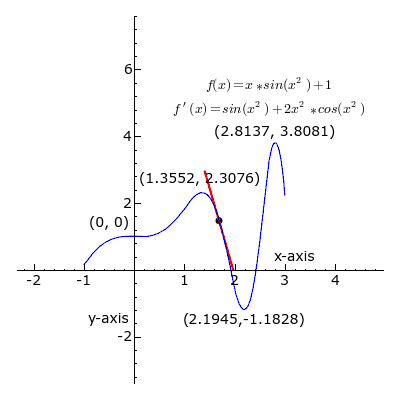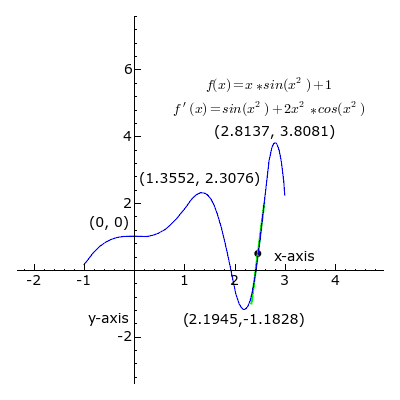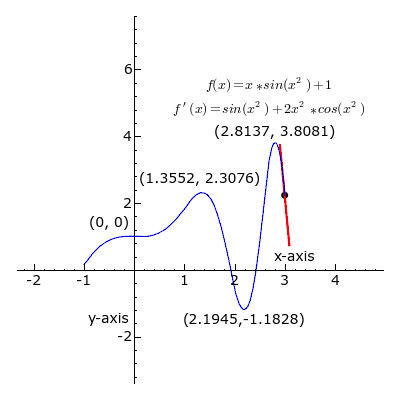
L'accroissement moyen d'une fonction sur un intervalle peut être utile pour une première approche, mais n’est pas forcément représentatif du comportement de la fonction sur cet intervalle. Prenons l'exemple de la fonction ci-dessous :

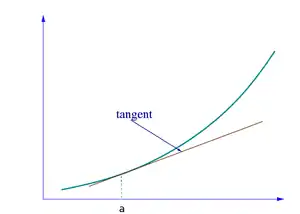
Entre A et B, les variations de la fonction sont beaucoup plus brutales que ne le laisse apparaître l'accroissement moyen. L'idéal serait de disposer d'un outil plus fin qui rendrait compte de l'accroissement en chaque point. Géométriquement, un tel outil existe : il s'agit de la tangente à une courbe en un point.

Le coefficient directeur de la tangente en un point A est ici la grandeur qui nous intéresse le plus, car il correspond à l'accroissement de la fonction au point A d'abscisse a.

Ce qu'on cherche à faire est donc : trouver un outil permettant d'obtenir l'accroissement d'une fonction, c'est-à-dire le coefficient directeur de la tangente à sa courbe, en tout point de l'intervalle de définition.

Définition du nombre dérivé

Soit $x\in I$

On cherche à trouver le coefficient directeur de la tangente à la courbe de ƒ au point d'abscisse x.

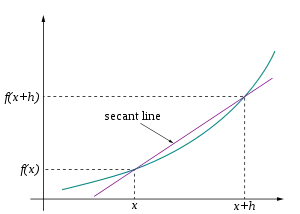
Pour ce faire, on réutilise la notion d'accroissement sur un intervalle $[x;x+h]$ où $h\in \mathbb {R}$ .

L'accroissement moyen de ƒ sur l'intervalle $[x;x+h]$ vaut ${\frac {f(x+h)-f(x)}{(x+h)-x}}={\frac {f(x+h)-f(x)}{h}}$

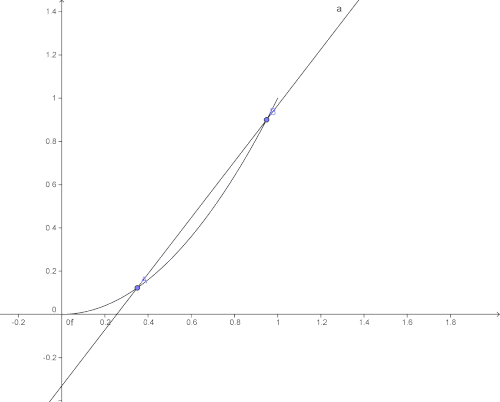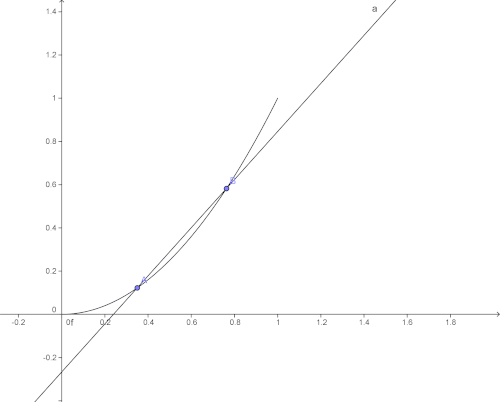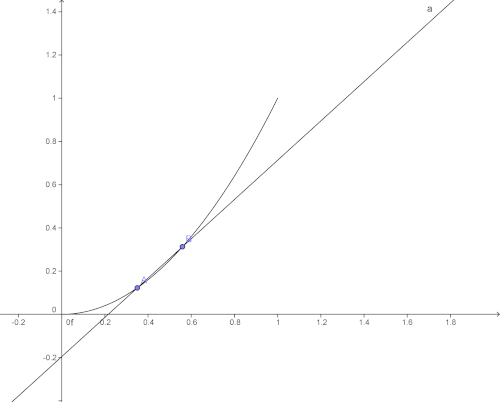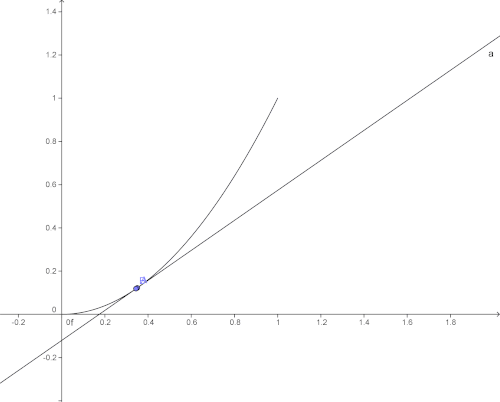
Comme ce qui nous intéresse est la tangente, et non une corde, on va diminuer h. Cette manipulation a pour effet de rapprocher les deux points A et B. On s'aperçoit alors que, ce faisant, la corde (AB) se rapproche de plus en plus de la position de la tangente en A à la courbe de ƒ.

Ainsi, lorsque h devient extrêmement petit :

(AB) se confond avec la tangente en A à la courbe de ƒ
l'accroissement moyen de ƒ sur l'intervalle $[x;x+h]$ vaut le coefficient directeur de la tangente en A à la courbe de ƒ

Voir les exercices sur : Cordes et tangentes.

On introduit ainsi la notion de nombre dérivé :

Définition

La limite de l'accroissement moyen de ƒ entre $a$ et $a+h$ lorsque $h$ tend vers 0 est appelée nombre dérivé de ƒ en $x=a$ et noté $f'(a)$ ^[1].

$f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$

Notation en physique

En mathématiques, on utilise la notation avec une prime pour désigner la dérivée.

En physique, on utilise plus couramment une autre notation, appelée notation différentielle. On note ${\frac {{\rm {d}}f}{{\rm {d}}x}}(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$ .

Le symbole « petit d » en physique signifie une petite variation de la grandeur qui suit le d. La notation ${\frac {{\rm {d}}f}{{\rm {d}}x}}(a)$ signifie donc qu'on considère :

une toute petite variation des valeurs de ƒ (dƒ), qui correspond à $f(a+h)-f(a)$ lorsque $h\to 0$ )
divisée par une toute petite variation des valeurs de x autour de a (dx, qui correspond à $(a+h)-(a)$ lorsque $h\to 0$ )
le tout au point d'abscisse a

Interprétation graphique

Propriété

$f'(a)$ est le coefficient directeur de la tangente à la courbe représentative de ƒ au point A.

Restrictions

Nous verrons par la suite que le nombre dérivé n'est pas toujours défini.

Définition

Si, en un point $a\in I,~f'(a)$ existe, on dit que ƒ est dérivable en a.

Notes

↑ ƒ '(a) se lit « f prime de a »

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] ƒ '(a) se lit « f prime de a »

[1]