désignera un intervalle réel et un ouvert de .
Exercice 1
Soit . On suppose que l'intervalle est compact et que pour tout , l'application est bornée (ce qui est le cas si elle est continue). Montrer l'équivalence entre :
- est localement lipschitzienne par rapport à sa deuxième variable ;
- ;
- .
On a clairement . Montrons que . Soit et pour tout , soient et tels que
.
Par compacité, est recouvert par un nombre fini de boules avec .
En prenant pour le plus grand des et pour le plus petit des , on a alors :
.
Pour traiter aussi le cas , remarquons que si et alors :
.
En posant , on a donc :
.
La propriété 3 est ainsi vérifiée, pour .
Exercice 2
Soient un espace de Banach, un ouvert de , une fonction localement lipschitzienne par rapport à sa seconde variable et continue, et une solution maximale de l'équation différentielle .
- Montrer que si est fini et si est bornée au voisinage de , alors admet au point une limite et le couple appartient à la frontière de .
- En déduire que si et si est inclus dans un compact de , alors .
- Si est bornée sur un intervalle de la forme alors — d'après l'inégalité des accroissements finis — est lipschitzienne sur cet intervalle. D'après le critère de Cauchy pour une fonction, admet alors au point une limite . Le couple est adhérent à l'ouvert mais ne lui appartient pas car sinon — d'après le théorème « limite de la dérivée » — serait prolongeable en une solution définie au point , ce qui contredirait sa maximalité.
- . Montrons par l'absurde que (on montrerait de même que ). Si alors est fini. On peut donc appliquer la question précédente, en utilisant que est à valeurs dans un compact et que sur le compact (avec assez petit pour que ), est continue donc bornée. On obtient alors un tel que , ce qui est absurde puisque .
Exercice 3
Soient une fonction continue, et une solution de telle que .
Montrer que .
Remarquons d'abord que
.
Par ailleurs, d'après le théorème des accroissements finis, pour de à on a :
.
Par passage à la limite, on en déduit que les composantes de sont nulles.
Exercice 4
Soit de classe C1 et bornée. Pour on note la solution de
.
- Montrer que cette solution est définie sur .
- Montrer que .
- Même argument que dans l'exercice 6 puisque, ici encore, est bornée.
- Fixons et , et notons le vecteur et l'application . Alors, et donc
, c'est-à-dire .
Exercice 5
Soit une solution d'une équation différentielle . Démontrer que si est de classe Cp alors est de classe Cp+1.
Montrons, par récurrence sur k variant de 0 à p + 1, que est définie et continue. C'est immédiat pour k = 0 ( est dérivable donc continue). Si c'est vrai pour un certain k ≤ p alors c'est encore vrai pour k + 1 car est de classe Ck, comme composée de et de .
Exercice 6
Référence : exo7.emath.fr/ficpdf/fic00053.pdf, Équations différentielles (énoncés : M. Queffélec, V. Mayer, T. Tahani, F. Sarkis ; corrections : F. Sarkis), exercice 3.
Soit . On considère le problème de Cauchy .
- Montrez qu'il existe une unique solution maximale et qu'elle est globale (c'est-à-dire définie sur ).
- Calculer la solution dans le cas .
- Étudier la régularité de cette solution.
- L'application est continue et lipschitzienne par rapport à donc le théorème de Cauchy-Lipschitz global s'applique.
- La solution est strictement croissante (puisque sa dérivée est ). Soit le plus grand intervalle sur lequel elle reste . Sur , on a , donc (revoir « Équation différentielle linéaire du premier ordre ») : , avec et .
Si , donc .
Si et , donc , qui s'annule en donc .
Sur , donc avec et , donc et . - Cette solution est au moins de classe C1 (cf. exercice précédent). Ailleurs qu'en et , elle est manifestement de classe C∞.
La restriction de à vérifie donc , en particulier .
La restriction de à vérifie , en particulier .
La restriction de à vérifie donc , en particulier .
Aux points et , n'est donc pas deux fois dérivable.
Exercice 7
Référence : exo7.emath.fr/ficpdf/fic00053.pdf, Équations différentielles (énoncés : M. Queffélec, V. Mayer, T. Tahani, F. Sarkis ; corrections : F. Sarkis), exercice 4.
Soit donnée par : si et . On s'intéresse à l'équation différentielle .
- Le théorème de Cauchy-Lipschitz local s'applique-t-il ?
- Soit une solution sur un intervalle ne contenant pas . On pose . Traduire l'équation différentielle sur par une équation différentielle sur et résoudre cette dernière.
- Que peut-on en déduire sur l'existence et l'unicité des solutions du problème de Cauchy ?
- Ailleurs qu'en , est C∞. En , elle est continue car , d'après l'inégalité , appliquée à et . Mais elle n'est lipschitzienne par rapport à sa seconde variable sur aucun voisinage de car équivaut, quand avec (par exemple ) à , non borné. Le théorème de Cauchy-Lipschitz local ne s'applique donc pas.
avec , ou .- a pour limite en lorsque dans on choisit . Chaque valeur de fournit alors une solution autre que la solution évidente . De plus, on peut recoller l'une de ces solutions à droite de avec n'importe quelle autre à gauche.
Exercice 8
Référence : Frédéric Paulin, « Topologie, analyse et calcul différentiel », , p. 260, lemme 7.22
Soient deux solutions de l'équation différentielle . On suppose que est -lipschitzienne par rapport à sa seconde variable sur la réunion des graphes de et . Démontrer que .
On utilisera le lemme suivant, qui est un exercice sur les propriétés de l'intégrale :
pour tous et , si une fonction continue vérifie , alors .
Notons et supposons, sans perte de généralité, et . Il s'agit alors de démontrer que .
Par hypothèse, donc (d'après l'inégalité des accroissements finis)
.
Grâce au lemme, on en déduit :
.
Exercice 9
On considère le problème de Cauchy
- .
- Montrer que la solution maximale est unique et globale.
- Pour quelles valeurs de est-elle constante ?
- Soit . Déterminer le comportement (monotonie ? limites ?) de la solution maximale du problème de Cauchy.
- Étudier de même le problème de Cauchy .
- donc est -lipschitzienne, de sorte que le théorème de Cauchy-Lipschitz global s'applique.
- Pour .
- Puisque les courbes intégrales ne se coupent pas, la solution reste dans donc donc est strictement croissante. Par conséquent (cf. exercice 3 ci-dessus) et (pour une résolution complète, voir l'exercice 29 de cette feuille).
- De même, est -lipschitzienne donc la solution maximale est unique et globale. Elle est constante pour . Si , la solution reste dans cet intervalle donc donc est strictement croissante donc et .
Exercice 10
On considère le problème de Cauchy
- .
- Montrer que la solution maximale est unique.
- Pour quelles valeurs de est-elle constante ?
- Comment la solution maximale de se déduit-elle de la solution maximale du problème de Cauchy ci-dessus ?
- Comment la solution maximale du problème de Cauchy ci-dessus pour chaque se déduit-elle de celle pour chaque ? On supposera donc désormais .
- Soit la solution maximale. Montrer que est (strictement) positive et croissante et en déduire et .
- Par le calcul, retrouver ces résultats et donner et .
- La fonction est-elle lipschitzienne sur ?
- On considère maintenant le problème de Cauchy non autonome
- .
- Montrer que la solution maximale est encore unique et qu'elle est C∞.
- On suppose toujours . Soit la solution maximale. Montrer que et en déduire que .
- La fonction est C1 (et même C∞) donc localement lipschitzienne, ce qui permet d'appliquer le théorème de Cauchy-Lipschitz local.
- Pour .
- En posant .
- En passant aux opposés.
- Si , puisque les courbes intégrales ne se coupent pas, la solution maximale reste dans donc donc est croissante. Par conséquent (cf. exercice 2 ci-dessus) et (cf. exercice 3 ci-dessus) .
- La solution de cette équation de Bernoulli est , qui croît de à .
- Non, puisque la solution maximale n'est pas globale. Mais on peut bien sûr le démontrer plus directement.
-
- La fonction est C∞ (car polynomiale).
- et donc il existe (et ) tel que au moins sur . Supposons que ne soit pas constamment et notons alors le plus petit réel (et ) en lequel . Alors, sur l'intervalle , donc , ce qui est impossible puisque aux deux extrémités. On a donc bien montré (par l'absurde) que . Puisque , ceci prouve que .
Exercice 11
- Résoudre .
- La fonction est-elle lipschitzienne sur un voisinage à gauche ou à droite de ?
- Sur un intervalle où , l'équation équivaut à donc les solutions sont :
- , avec arbitraire.
- De même, les solutions sont :
- , avec arbitraire.
- Le prolongement de ces solutions partielles par la fonction constante nulle est dérivable au point de recollement.
- Par conséquent, les solutions sur sont toutes les fonctions de la forme :
- ,
avec arbitraires.
- ,
- Non, puisque pour tout voisinage à gauche ou à droite de , le problème de Cauchy a une infinité de solutions maximales à valeurs dans . Mais on peut bien sûr le démontrer plus directement.
Exercice 12
I. Soient . On considère le système
- Montrer que la solution maximale est unique.
- Résoudre le problème de Cauchy pour .
- Résoudre le problème de Cauchy pour .
- En déduire que si alors .
- On considère . Toujours dans le cas , montrer que la fonction est constante et en déduire que la solution maximale est globale.
- La fonction est C1 (et même C∞ car polynomiale) donc localement lipschitzienne, ce qui permet d'appliquer le théorème de Cauchy-Lipschitz local.
- Si , la solution est .
- Si , la solution est .
- Par conséquent, si alors ne s'annulent jamais donc restent .
- Sur l'intervalle de définition de , donc est constante, ce qui, vue sa forme, garantit que est bornée. Par conséquent (cf. exercice 2 ci-dessus), .
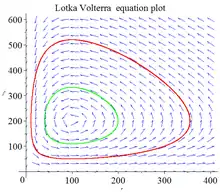
II. On suppose toujours .
- Déterminer les signes de et selon la zone de dans laquelle se trouve .
- On suppose par exemple que et . Montrer qu'il existe un premier instant tel que et qu'alors, et .
- Montrer qu'il existe un premier instant tel que et qu'alors, et .
- Montrer qu'il existe un premier instant tel que et qu'alors, et .
- Montrer qu'il existe un premier instant tel que et qu'alors, et .
- Montrer enfin qu'il existe un premier instant tel que et qu'alors, .
- Vérifier que l'application est injective et en déduire que est -périodique.
- est du signe de et est du signe de .
- ne peut pas rester indéfiniment dans car dans cette zone, décroît et croît donc on aurait (cf. exercice 3 ci-dessus) avec , et , ce qui est incompatible. Toujours par croissance de et décroissance de , au premier instant auquel appartient à la frontière de cette zone, on a et bien sûr, donc .
- À l'instant , passe dans la zone , dans laquelle et croissent (mais restent bornés). Puis, mêmes arguments que précédemment.
- À l'instant , passe dans la zone , dans laquelle décroît et croît (mais reste borné). Puis, mêmes arguments que précédemment.
- À l'instant , passe dans la zone , dans laquelle et décroissent. Puis, mêmes arguments que précédemment.
- À l'instant , revient dans la zone de départ . Puis, mêmes arguments que précédemment.
- L'application est strictement décroissante (car sa dérivée est ) donc injective, donc .
III. Calculer les valeurs moyennes de et sur une période.
Soit la période. La valeur moyenne de est
- .
De même, celle de est . Remarquons (ce qui était prévisible…) que si l'on augmente la mortalité des prédateurs, la population moyenne des proies augmente, et que si l'on diminue le taux de reproduction des proies, la population moyenne des prédateurs diminue.
Exercice 13
On s'intéresse au problème de Cauchy (scalaire d'ordre 2) :
- .
- L'exprimer sous forme vectorielle d'ordre 1 et montrer qu'il a une unique solution maximale, .
- Déterminer les solutions stationnaires.
- On considère . Montrer que est constante.
- On suppose dans la suite et , donc .

- Montrer que est impaire.
- Montrer que si , il existe tel que .
- Montrer que si , la solution est périodique.
- Décrire la solution si .
- avec .
est bornée donc est lipschitzienne. - Les solutions stationnaires correspondent à .
- .
- Sur tout intervalle centré en sur lequel la vitesse angulaire ne s'annule pas, elle reste positive donc égale à .
- Posons . Alors, , , et donc (par unicité de la solution maximale du problème de Cauchy) .
- Si , l'angle atteint la valeur à l'instant (qui est fini, car c'est l'intégrale d'une fonction continue sur ). On démontre facilement (par la même méthode que dans la question 4.1) que .
- Si , atteint pour la première fois sa valeur maximum à l'instant .
est fini car cette intégrale est impropre en mais convergente ; en effet, quand , en utilisant par exemple une formule de Simpson, on trouve que est équivalent à , qui est intégrable en .
D'après la question 3, . On démontre alors facilement (par la même méthode que dans la question 4.1) que . Comme elle est de plus impaire, la solution est donc -périodique. - Si , atteint la valeur en un temps . En effet, quand , est équivalent à , qui n'est pas intégrable en .
Exercice 14
Soient une fonction continue impaire et . On considère le problème de Cauchy
- .
- Justifier que ce problème a une unique solution maximale, qu'on note encore .
- Montrer que est définie sur .
- Montrer que si s'annule en un point alors elle est partout nulle. En déduire que est de signe constant.
- Montrer que est encore solution. En déduire que est paire.
- La fonction est continue, et localement lipschitzienne par rapport à puisque sa dérivée partielle par rapport à , , est continue donc localement bornée.
- La lipschitzianité par rapport à est locale par rapport à mais globale par rapport à car . On peut donc invoquer le théorème de Cauchy-Lipschitz global.
- Si s'annule en un point alors elle est égale à la fonction nulle, par unicité de la solution maximale du problème de Cauchy . Si elle ne s'annule nulle part alors elle est de signe constant, par continuité.
- Soit . Alors, et donc est solution donc (par unicité) , autrement dit : est paire.