Histoire de la mécanique
L'histoire de la mécanique débute réellement avec Galilée. Mais cette science prend ses racines dans des savoirs bien plus anciens, notamment avec les réflexions d'Archimède ou d'Aristote.
Jusqu'au XIXe siècle, la notion de mécanique englobait aussi bien l'étude scientifique des corps en mouvement que la théorie des machines.
Étymologie du mot mécanique
Si le mot apparaît à la Renaissance dans son sens moderne[1], cette science plonge cependant ses racines en des temps beaucoup plus anciens et son histoire est indissociable de celle de l'astronomie ou de l'art de fabriquer des machines.
Vitruve utilise le terme machinatio pour désigner la troisième partie de son De architectura : partes ipsius architecturae sunt tres : aedificatio, gnomonice, machinatio - mot qui n'est attesté en latin qu'à partir du milieu du Ier siècle, c'est-à-dire à peu près à l'époque où Vitruve doit commencer à rédiger son traité. Vitruve est donc le seul auteur connu à employer machinatio pour désigner une discipline (qu'elle soit scientifique ou technique) et a fortiori le seul à faire de cette discipline une des parties de l'architecture. Ce n'est pas d'après les principes de la géométrie, ni d'après ceux de la physique que Vitruve cherche à démontrer, dans le troisième chapitre, comment les machines produisent leurs effets[2]; il se contente de faire connaître ces machines, et d'expliquer par certaines expériences les effets qu'elles produisent.
Au terme machinatio, correspond en grec le terme Μηχανικά (Mékanika) auquel correspond un corpus d’œuvres du même nom. Selon Aristote, la μηχανή (mèkané) est la partie de la technique qui vient à notre secours chaque fois qu'il faut faire quelque chose contre la nature, et que l'on est embarrassé par la difficulté. La théorie mécanique (ή μηχανική θεωρία) selon Pappus d'Alexandrie (IVe siècle), « étant utile aux choses multiples et importantes qui se présentent dans la vie, elle mérite à juste titre la plus grande faveur chez les philosophes (προς των φιλοσόφων) et fait l'ambition de tous les mathématiciens (από των μαθημάτων), parce qu'elle est pour ainsi dire la première qui s'applique aux recherches physiques sur la matière constituant les éléments du monde. Cette théorie, organisée au moyen de théorèmes dominés par la matière elle-même, fournit la raison des corps qui se meuvent de par nature et elle en force d'autres en des mouvements de sens opposés, à se déplacer contre nature hors des lieux qui leur sont propres[2] ». Le grammairien Audax classant les arts en trois catégories : ceux qui appartiennent à l'esprit, ceux qui appartiennent au corps et ceux qui appartiennent aux deux, range la mechanica dans cette dernière catégorie. Le mécanicien, praticien ou théoricien est nommé mechanicus[2].
Si l'on poursuit l'enquête terminologique avec les mots de la famille de machina, on s'aperçoit que pour les Romains c'est Archimède qui est généralement associé à la notion de mécanique. Il y a donc bien eu chez les Romains conscience d'une discipline mécanique, mais, hormis chez Vitruve, nous ne trouvons ni définition claire, ni traité qui lui soit exclusivement consacré[2].
Les fondements de la mécanique, en tant que science et au sens moderne du terme, sont posés par Galilée ( 1632 les Dialogues, 1638 les Discours ). Elle n'est alors pas dissociée des arts mécaniques, c'est-à-dire des techniques de construction des machines. En 1559, le mot désigne ainsi « la partie des mathématiques qui a pour objet la connaissance des lois du mouvement et la théorie de l'action des machines »[3]. On désignera un peu plus tard du nom de mécanicien (attesté en 1696) la personne qui « possède la science de la mécanique et celle qui invente, calcule, construit des machines »[3]. Ce n'est qu'au XIXe siècle, à partir de 1840, que ce terme désigne « celui ou celle qui monte et entretient des machines »[3], et que la distinction se fait plus nettement entre la mécanique en tant science et la mécanique en tant que technique.
Isaac Newton dans la préface de ses Philosophiae naturalis principia mathematica (1687), remarque qu’on doit distinguer deux sortes de mécaniques, l’une pratique, l’autre rationnelle ou spéculative, qui procède dans ses opérations par des démonstrations exactes; la mécanique pratique renferme tous les arts manuels qui lui ont donné leur nom. Mais comme les artistes et les ouvriers ont coutume d’opérer avec peu d’exactitude, on a distingué la Mécanique de la Géométrie, en rapportant tout ce qui est exact à la géométrie, et ce qui l’est moins à la mécanique. Ainsi Newton remarque que les descriptions des lignes et des figures dans la géométrie, appartiennent à la Mécanique(...) Par conséquent, la géométrie est fondée sur des pratiques mécaniques, et elle n’est autre chose que cette pratique de la Mécanique universelle, qui explique et qui démontre l’art de mesurer exactement. L'Encyclopédie ajoute à ce propos que la Méchanique rationnelle tire beaucoup de secours de la géométrie, la géométrie en tire aussi quelquefois de la mécanique, etc.[4]. Charles Bossut qui collabore avec D'Alembert à la rédaction de l'Encyclopédie (1751) accepte la conception d'une mécanique théorique bâtie sur le modèle de la géométrie prônée par ce dernier, toutefois il conçoit qu'il y ait une mécanique pratique où il est impossible d'appliquer les « formules compliquées » de la théorie la plus récente[5]: Le jugement d'Archimède dit-il dans son Histoire générale des mathématiques (1810), « sur l'excellence de la géométrie doit s'étendre également à la mécanique rationnelle et théorique. Car les vérités qu'elle démontre sont aussi certaines, aussi intellectuelles et quelquefois (sic) aussi profondes que celles de la géométrie pure. Mais il n'est pas permis de placer sur la même ligne la mécanique pratique, puisqu'un homme qui était tout à la fois un grand géomètre et un grand machiniste [Archimède] nous le défend d'une manière si positive. Cependant, elle demande souvent beaucoup d'esprit et d'invention et assurément un machiniste de premier ordre l'emporte sur un géomètre ordinaire »
Pour l'Encyclopédie, la partie des mécaniques qui considère le mouvement des corps, en tant qu’il vient de leur pesanteur, s’appelle quelquefois statique par opposition à la partie qui considère les forces mouvantes et leur application, laquelle est nommée par ces mêmes auteurs Méchanique. Mais on appelle plus proprement statique, la partie de la Mécanique qui considère les corps et les puissances dans un état d’équilibre, et Mécanique la partie qui les considère en mouvement[4].
Les prémices de la mécanique
Aux origines, la mécanique, qui ne porte pas encore ce nom, regroupe les réflexions, encore d'ordre philosophique ou religieux, visant notamment à expliquer les mouvements des astres. La régularité des mouvements des objets célestes n'échappe pas aux premiers astronomes, qui conçoivent alors le ciel et ses mobiles comme une sorte de gigantesque machine.
« L'historiographie contemporaine volontiers conceptualisante, a produit une abondante littérature autour des notions de technique et de technologie antiques, où l'on trouve, pêle-mêle, de nombreuses et longues méditations sur l'existence d'une pensée technique dans l'Antiquité, l'efficacité ou non de la technologie, son éventuelle stagnation, ses blocages, sa capacité d'application pratique de théories élaborées intellectuellement, ... en liaison ou non avec les schémas ou courants mentaux, psychologiques ou sociologiques des sociétés anciennes, l'esclavage et les modes de production, l'idée de profit, de progrès ou de développement. ». Beaucoup d'études comme celle Richard Lefebvre des Noëttes - largement invalidée depuis - concluent à la médiocrité technique du monde grec[6]. Des deux erreurs de fond commises par Aristote dans la dynamique du corps solide, la première, la loi de la vitesse proportionnelle au rapport de la force à la résistance, n'a pas été reconnue par l'antiquité. Aucun des penseurs grecs qui ont cherché après le Stagirite à pénétrer dans les secrets du mouvement, même pas Archimède, n'est arrivé à dégager la notion fondamentale qui est la clef de l'explication des phénomènes dynamiques, la notion d'inertie. Aristote en frôle parfois de près la découverte, sans jamais y arriver. « Archimède, que ses dispositions géniales pour l'analyse mathématique, ses aptitudes pour l'observation et ses dons d'expérimentateur auraient qualifié comme aucun autre des grands géomètres grecs après Aristote à faire le pas décisif pour créer la dynamique du corps solide, a laissé subsister, certes, lui aussi, la théorie aristotélicienne du mouvement, parce que la mort violente qu'on connaît l'a arraché à ses travaux avant qu'il n'ait pu dégager de ses recherches sur les conditions d'équilibre la notion clef d'inertie[7]. » Ceci et d'autres choix malheureux fait par Aristote notamment la réfutation du vide, de l'espace euclidien, Aristote placé aux nues par ses successeurs, engageront la science dans une impasse qui durera jusqu'à Galilée. Quand Galilée, au seuil des temps modernes, établira une théorie rigoureuse des lois du mouvement fondée sur l'expérience, il aura à lutter au travers de la scolastique contre l'autorité d'Aristote.
Le savoir dans l'Antiquité consistait en le savoir de la réalité physique tout autant que la métaphysique et le savoir des choses divines. Elle avait inauguré deux groupes de disciplines : les disciplines appelées alors mathématiques et la philosophie. Les mathématiques consistaient en « mathématiques pures » — arithmétique et géométrie — mais aussi la mathématique « appliquée » : « astronomie, un peu de statique, quelques rudiments d'optique ou d'acoustique ». Le propos de la philosophie spéculative, était d'embrasser intellectuellement la totalité de l'être et d'en développer convenablement la compréhension. Une de ses branches principales était la « philosophie naturelle ». Cette dernière traitait de façon raisonnée de l'univers sensible et de tout ce qui s'y présente à l'observation humaine. Par là, la philosophie naturelle se trouvait en concurrence avec l'étude mathématique de la réalité sensible, et aussi l'astronomie. Ce fait de concurrence ne posa guère de problèmes parce que le ciel relevait d'une région de nature incorruptible, glorieuse et quasi divine qui n'interférait donc pas avec la nature des choses d'ici-bas. Il y avait donc concordance entre l'enseignement « mathématique » des astronomes scientifiques et l'enseignement « philosophique » des physiciens spéculant sur le cosmos. La philosophie naturelle d'Aristote, dont la tradition fut prépondérante au sein de l'Occident médiéval et jusqu'au temps de Galilée, avait tenu compte, du plus près qu'il lui avait été possible de le faire, de l'acquis de l'astronomie mathématique de l'époque à laquelle elle s'était elle-même constituée. La divergence entre spéculation philosophique et science mathématique de la nature n'apparut qu'ensuite[8].
La physique d'Aristote
La physique d'Aristote (-384, -322) concordait avec l'astronomie d'Eudoxe de Cnide et de son successeur Callippe de Cyzique, mathématiciens et astronomes du IVe siècle. Elle ne concordait plus déjà avec l'astronomie de Claude Ptolémée, astronome du IIe siècle, dans l'œuvre duquel se rassemble tout l'acquis de la science astronomique ancienne[8].
C'est Aristote qui posera le premier les bases d'une véritable théorie mécanique. Tous les corps de l'univers tirent selon lui l'origine de leur mouvement d'un premier moteur, les mouvements étant transmis par contact. À cela s'ajoute l'idée que les objets se meuvent pour atteindre le lieu propre qui leur est destiné, où ils trouveront l'immobilité.
La théorie du mouvement d'Aristote comporte de nombreuses difficultés dont le Stagirite était bien conscient. L'une des principales portait sur le mouvement de la flèche, dont on ne comprenait pas ce par quoi elle pouvait être portée après avoir été lancée par l'archer. Les idées d'Aristote domineront cependant largement la manière de concevoir le mouvement jusqu'au début du second millénaire, en l'absence de théorie alternative véritablement plus crédible.
L'histoire vouera à Aristote une foi aveugle dans sa supériorité sur tous les autres représentants du génie grec. Relayé par la scolastique médiévale, certains principes de la dynamique aristotélicienne dont les fondements sont faux, survivront jusqu'au XVIIe siècle sous la forme de l'Alchimie. De manière triviale, ce sont les nouveaux besoins de précision que réclament l’artillerie XIVe siècle qui feront apparaître les théories encore en usage totalement inapte à décrire le mouvement comme la trajectoire des boulets de canons. Sous l'impulsion d'un Jean Buridan ou des Calculateurs d'Oxford, les théories de l'Impetus introduiront progressivement la notion de quantité de mouvement dans un référentiel encore largement hérité de la physique d'Aristote et donc non valide. Il faudra enfin le génie d'un Galilée pour que l'état de mouvement d'un corps soustrait à toute force soit reconnu comme celui d'un mouvement rectiligne et uniforme, introduction au principe d'inertie sur lequel Isaac Newton viendra fonder la mécanique moderne[7].
L'école d'Alexandrie
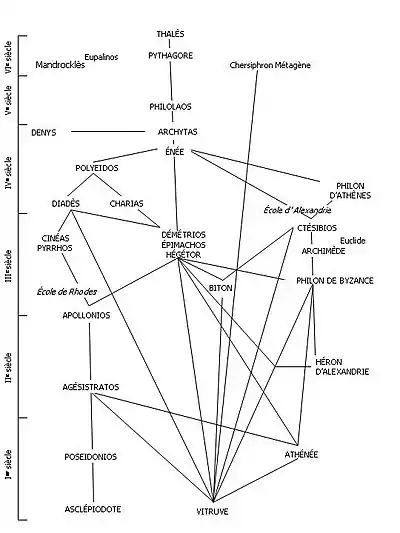
L'apparition des catapultes (siège de Motyé par Denys l'Ancien en -397), des balistes et, plus encore, un début de rationalisation de leur fabrication, sont autant d'éléments qui prouvent un tournant considérable de la science grecque. Si l'on rationalise, si l'on étend le champ des connaissances techniques et les premiers symptômes de liaison avec les sciences, les premiers traités techniques pouvaient faire leur entrée en scène, même s'il est encore difficile de parler de technologie, tout comme Chersiphron et Métagénès avaient pu le faire pour les appareils de levage. L'ingénieur Diadès est associée au succès d'Alexandre le Grand, notamment les sièges de Périnthe et de Tyr. Notons Epimachos l'athénien ingénieur de Démétrios Ier Poliorcète, inventeur de l'hélépole employé au siège de Rhodes en -305. Ainsi naissait une tradition d'auteurs et de traités[9]. .
Nous sommes à la fin d'un intense mouvement scientifique, plus ou moins bien orienté, selon les disciplines. Il en est de même en matière technique, dans le domaine des machines, de la mécanique. À partir de -288, Ptolémée Ier inaugure l'école d'Alexandrie. La bibliothèque d'Alexandrie s'ingénie à rassembler dans la ville tout ce que le monde grec a produit de plus remarquable dans tous les domaines. Euclide arrivé à Alexandrie vers 300 construit un nouveau livre de géométrie. On lui devrait encore un ouvrage de mécanique sur les leviers et les poids. On y rencontre également Straton de Lampsaque, aurait reconnu la proportionnalité de la pesanteur à la masse, la loi d'accélération de certains phénomènes naturels. À La première génération de l'école d'Alexandrie qui fait de louables efforts pour systématiser les connaissances scientifiques, succède Eratosthène, et des génies comme Archimède[9].
La science d'Alexandrie sort de la science formelle et abstraite que l'on connaissait auparavant. Seule, la géométrie est hissée au rang de science pure, engendrant ses propres démonstrations. Aussi n'est-il pas étonnant que beaucoup des autres sciences et les techniques aient cherché à se réduire à une géométrie[9].
Le fondateur supposé de l'école des mécaniciens d'Alexandrie, Ctésibios, avec Archimède est cité par Vitruve comme l'un des auteurs essentiels à la formation des ingénieurs et parmi les mécaniciens célèbres de l'Antiquité. On lui doit la pompe aspirante et foulante ainsi que d'autres machines[9].
Avec Philon de Byzance apparaît pour la première fois dans son ensemble ce qu'on a appelé la syntaxe mécanique, sorte d'encyclopédie mécanique qui était dans le style de ce qui se faisait à Alexandrie. Traité des leviers; Pneumatiques; Traité des automates; Traité des instruments merveilleux (orgues et tuyaux); Traité de la traction des poids lourds (Baroulkos); Traité des clepsydres; Traité de la construction des ports; Traité de fortification; Traité des machines de guerre; Traité des roues qui se meuvent d'elles-mêmes dont certains nous sont parvenus. Les pneumatiques commence par un ensemble de théories sur la nature de l'air, sur son rapport et sa « jonction » avec l'eau, sur l'inexistence du vide. Le traité des machines de guerre apporte une rationalisation de la fabrication des machines et aboutit à une formule chiffrée, mettant en rapport le diamètre du faisceau de fibres élastiques et le poids du projectile , d'une richesse de pensée technique mise en évidence par Victor Prou[9].
La statique d'Archimède
Les contributions d'Archimède (-287,-212) à la construction d'une science mécanique, alors encore en devenir, sont absolument fondamentales. C'est notamment à partir de ses réflexions sur l'équilibre des corps que Galilée posera les bases de la mécanique moderne. Il ne s'agit pas encore d'une théorie du mouvement, mais d'une mécanique statique, c'est-à-dire d'une science visant à comprendre l'agencement des corps au repos.
Déclin de la mécanique
Le développement de la technique grecque semble s'être arrêté avec les derniers représentants de l'école d'Alexandrie. La primauté de la science sur les techniques et le mépris du travail manuel et, par conséquent, de la technique sont invoqués comme cause. Les Romains ne furent guère des novateurs en matière technique. Seul Vitruve nous donne, à la fin de son traité d'architecture, le bilan de la mécanique utilisée de son temps., toujours affaire d'approximation.
Science médiévale
L’Europe redécouvre les écrits antiques, notamment au travers des auteurs arabes.
Dominique Gundissalvi ajoute aux quatre sciences mathématiques (quadrivium) que sont l'arithmétique, la musique, la géométrie et l'astronomie, l'optique (la perspective), la science du poids (scientia de ponderibus), la science de la construction des instruments ou engins (Scientia de ingeniis)[10]. Saint Thomas d'Aquin leurs ajoutent la science des sphères se mouvant (Scientia de sphaera mota)[11],[12].
La Scientia de ponderibus
La Scientia de ponderibus (du latin pondus, le poids) est la science du poids médiévale, à laquelle correspond un ensemble de traités, dont celui de Jordanus Nemorarius (1225 - 1260), les Elementa Jordani super demonstrationem ponderum. Il y est question de l'équilibre de la balance romaine et sur le même principe de tous leviers. Pierre Duhem a vu dans cet ouvrage les prémices de la statique [13].
L'Impetus
La notion d'impetus vise en particulier à répondre aux apories de la théorie d'Aristote. L'impetus est une sorte de vertu motrice qui se consomme et s'épuise à mesure qu'un corps se meut. Bien que intuitivement assez proche de la notion d'énergie cinétique, l'impetus en était en fait très éloigné, car elle continuait à porter l'idée de mouvement absolu (et donc l'idée d'une possible immobilité absolue). Dans cette théorie, il y a une différence de nature entre l'objet mobile, porteur d'un certain impetus, et l'objet immobile, sans impetus. Il faut attendre Galilée pour dépasser ces conceptions erronées du mouvement.
La statique de Simon Stevin
Le traité d'hydrostatique de Simon Stevin a paru d'abord en hollandais à Leyde en 1586: De Beghinselen des Waterwichts a été de nouveau publié dans ses œuvres mathématiques écrites, également en hollandais, à Leyde, de 1605 à 1608. Willebrord Snell les a traduites en latin. Il a rendu le hollandais Waterwicht par hydrostatice expliqué en marge par aquam ponderare et c'est par là que ce terme s'est introduit dans l'usage[14].
Stevin démontre bien avant Blaise Pascal le Paradoxe hydrostatique. Découlant de son expérience de la Clootcransbewijs, le théorème de Stevin sur l'équilibre de trois forces parallèles et proportionnelles aux trois côtés d'un triangle quelconque aura pour conséquence le principe de la composition des forces de Pierre Varignon énoncé en 1688, ou plutôt il n'est que ce même principe présenté sous une autre forme[15]
La mécanique Galiléenne
Le mérite global de Galilée (1564-1642), est d'avoir discerné, « dans le matériel encore diffus de l'expérience et des expériences postérieures à la fixation de la physique ancienne, ce qui était de l'importance la plus grande et de l'avoir amené de façon décisive à la clarté de la conception scientifique : continuation inertiale du mouvement, chute des corps, première dynamique de la force, mouvement d'un projectile dans un champ de pesanteur, comportement du pendule. Cela suffisait, en effet, pour jeter les premières bases d'une vraie mécanique scientifique du corps isolé, et, avec elle, faire naître un premier regard vraiment scientifique sur l'univers dont la science physique moderne allait prendre possession. » L’expérimentation mise en place par Galilée, véritable reconstruction rationnelle à partir des principes scientifiques qu'il assume présage l'expérimentation scientifique moderne. C'est aussi l'expérience de ceux qui ne se satisfont plus des premières organisations de l'appréhension sensible du réel et qui sait déjà que les premières apparences empiriques retenues par la physique ancienne renforcée par la tradition ne livrent pas le secret de la vérité des choses[8].
S'inspirant des travaux de Giovanni Battista Benedetti[16] (1530-1590), Galilée observe par exemple la chute libre des corps pesants et il arrive à penser le caractère uniformément accéléré de ce mouvement. Il connaît par ailleurs la statique du plan incliné et les lois de l'équilibre d'un corps pesant placé sur celui-ci. A partir de quoi, pensant au mouvement de descente d'une bille roulant sur le plan incliné, il est en mesure de combiner ces deux connaissances et de démontrer alors que ce mouvement sera, lui aussi, un mouvement uniformément accéléré, mais dont l'accélération constante sera moindre que celle à laquelle le mouvement est soumis dans le cas de la chute libre. Les choses se passant plus lentement seront donc plus faciles à observer[8].
La science physique moderne commence avec Galilée au moment où, dans les Discorsi e dimostrazioni matemaliche intorno a due nuove scienze, celui-ci réussit à poser les premiers fondements et à rassembler quelques éléments d'une mécanique correctement mathématisée[8]. La vie de Galilée comme son expérience intellectuelle témoigne de l'effondrement proche du système de la philosophie naturelle scolastique.
Galilée vs Aristote
Aristote suppose qu'un mobile dix fois plus lourd qu'un autre se mouvra dix fois plus vite et tombera dès lors deux fois plus rapidement. Toujours de manière erronée il s'insurge contre certains anciens qui introduisirent le vide comme nécessaire au mouvement, en disant que sans celui-ci, le mouvement ne pourrait avoir lieu. Déduisant de la difficulté qu'un mobile éprouve à se mouvoir dans un milieu dense - il postule que la vitesse dans l'air par rapport à la vitesse dans l'eau est dans le rapport inverse de leurs densités et d'autre-part que si le vide pouvait exister, le mouvement se ferait en un instant, ce qui est impossible. Par conséquent en vertu de l'existence du mouvement, il est impossible qu'il y ait du vide. Tout corps grave qui tombe possède selon Aristote une certaine vitesse, déterminée par la nature, et que l'on ne peut ni accroître ni diminuer, si ce n'est en usant de la violence ou en lui opposant une résistance[17]. Toutes ces assertions sont battues en brèches par Galilée.
La loi de la chute des corps professée par Galilée dans son De Motu, qui sonne le glas de la physique aristotélicienne, comporte deux assertions qui, bien qu'étroitement liées dans l'esprit de Galilée, peuvent être distinguées de cette manière: La première affirme que ce mouvement obéit à la loi du nombre et que les espaces traversés dans des intervalles successifs (et égaux) du temps sont ut numeri impares ab unitate: Dans le mouvement de la chute, les vitesses croissent proportionnellement au temps comme les nombres, les espaces parcourus dans les intervalles successifs, comme les nombres impairs, et les espaces parcourus depuis le commencement de la chute, comme les carrés. En d'autres termes, à l'encontre de ce qu'avait enseigné Aristote, une force détermine non pas un mouvement uniforme, mais un mouvement uniformément accéléré, et l'action de la force motrice produit non pas une vitesse, mais une accélération. La deuxième ajoute que dans leur mouvement de chute, également à l'encontre d'Aristote, tous les corps, grands et petits, lourds et légers, c'est-à-dire quelles que soient leurs dimensions et leurs natures, tombent, en principe, sinon en fait (Pour que l'assertion soit vérifiée de manière complète, elle doit être réalisée dans le vide), avec la même vitesse; Pour Galilée qui n'admet pas d'attraction terrestre comme le fera Newton, l'accélération de la chute est une constante universelle[17].
Ce qu'a montré Galilée, c'est que la force d'inertie (qui est fonction de la masse) compense exactement le poids de l'objet (lui aussi fonction de la masse): un objet plus lourd devrait tomber plus vite, mais comme il est plus difficile à mettre en mouvement, il tombe à la même vitesse qu'un objet plus léger. La formule qui lie la vitesse d'un corps en chute libre à la gravité, que l'on retrouve dans la formule de Torricelli , ne fait donc pas intervenir le poids. La masse d'un corps physique renvoie donc à deux natures phénoménologiques distinctes: La masse grave est la propriété de la matière qui se manifeste par l'attraction universelle des corps, et au quotidien, par leur poids et la masse inerte, la propriété de la matière qui se manifeste par l'inertie des corps.
L'expérience réalisée par Galilée selon la légende du haut de la tour de Pise est renouvelée par Apollo 15 dans atmosphère insignifiante de la Lune.
La mécanique relationnelle de Newton
Avant Newton, le poids désignait essentiellement une qualité: Le grave (le corps doué de poids), le corps pesant lui-même employé dans les horloges, ainsi qu'une grandeur caractérisant ce dernier mesuré en livre. La notion présentait un aspect statique : l'équilibre de la balance ; et un aspect dynamique : la propension à descendre. La gravité, ou pesanteur, d'autre part était une qualité ; c'était le fait pour un corps d'être lourd. On la considérait volontiers comme la cause de la descente des corps la possédant. Galilée n'avait guère bouleversé cette conception. Il avait surtout proposé une description mathématique de la chute des graves en l'absence, tout hypothétique, de résistance de l'air. Avec Newton, un poids est encore en partie ce qu'il était auparavant: un corps pesant; ou bien une grandeur, qui est alors une force motrice imprimée à ce corps, d'où lui vient sa propension au mouvement vers le bas[18].
En revanche, la conception du poids et de la gravité comme qualités, ou du moins comme qualités premières, n'est plus de mise parce que le contexte cosmologique a changé. Certaines idées séduisent les gens d'esprit, souvent formulées par Descartes dans toute leur ampleur. Celles qui se sont condensées dans la première loi du mouvement, le principe d'inertie, obligent à penser la chute des corps comme effet d'une action et non plus comme un mouvement naturel, puisque le mouvement de chute n'est pas uniforme. L'idée d'une physique mécaniste tend d'autre-part à s'imposer pour laquelle, à une telle action, il faut chercher des causes physiques[18].
Isaac Newton (1643 - 1727), va penser la masse en rapport avec la force et l'accélération : elle est le quotient de ces deux réalités.
Le corps est, non seulement ce qui remplit le lieu, comme le pose le De Gravitatione (1665), mais aussi « la quantité de matière qui se mesure à partir de la densité et du volume ». De même, le mouvement n'est plus seulement le changement de lieu, comme en 1665: sa quantité est évaluée à partir de l'espace et du temps et comme effet d'une force d'intensité et de direction données. Enfin, et surtout, sont clarifiés le concept de « force » et ses espèces, inertie ou vis impressa (force centripète notamment): telle est la véritable cause du mouvement, ce qui permet de le produire ou de le détruire ou de le maintenir rationnellement. C'est le couple mouvement-force qui permet de porter la mécanique au rang de science, parce que ses concepts de base sont susceptibles d'être exprimés par des « quantités », soit traduits mathématiquement. D'où cette définition dans la préface à la première édition des Principia[19]:
« La mécanique rationnelle est la science des mouvements qui résultent de forces quelconques et des forces qui sont requises pour des mouvements quelconques. »

En utilisant les résultats des observations de comètes, communes à cette époque, dont plusieurs effectuées par lui-même, Newton élabora la théorie du mouvement des comètes dans le cadre de sa loi de la gravitation universelle et établit ainsi pour la première fois leur appartenance au système solaire. Dans la première édition de ses Principia, Newton hésitait à attribuer aux orbites cométaires la forme de paraboles ou celle d'ellipses très allongées, plus apparentées aux trajectoires des planètes. La seconde des hypothèses envisagées par Newton reçoit un appui décisif lorsqu'en 1695 l'un de ses amis, l'astronome et mathématicien Edmond Halley (1656-1742), se persuade de l'identité probable de certaines comètes dont il s'était efforcé de calculer les éléments de trajectoires. Annoncé par Halley en 1705 et précisé par Alexis Claude Clairaut en novembre 1758, le retour de la « comète de 1682 » observée à l'époque par Halley lui-même, et qui sera bientôt appelée « comète de Halley », se réalisa le 13 mars 1759, date du passage de la comète à son périhélie. La valeur symbolique du retour de cet astre - qui n'est pas le plus remarquable ni le plus étudié - et qui lui valut une place privilégiée aussi bien dans les observations des astronomes que dans l'attention d'un vaste public, tient au fait qu'il s'agit du premier retour prévu d'une comète et pour le monde scientifique, qu'il s'agit de la plus éclatante vérification de la loi de gravitation universelle, tandis que sont définitivement éclaircis les principes de la théorie des comètes. En tenant compte des études théoriques de Joseph-Louis Lagrange (1736 - 1813), Pierre-Simon de Laplace (1749-1827), Carl Friedrich Gauss (1777-1855), le retour suivant de cette comète, celui de 1835, fut l'objet de plusieurs prévisions, dont les meilleures se révélèrent exactes à trois ou quatre jours près. La technique actuelle de calcul des orbites cométaires reprend avec de puissants ordinateurs la méthode de variation des éléments de la trajectoire introduite par Philip Herbert Cowell (en) et Andrew Crommelin (1865–1939) en 1910, mais en ajoutant à l'ensemble des forces de gravitation classiques agissant sur la comète, des forces complémentaires non gravitationnelles de réaction, dues à l'éjection de matière cométaire sous l'action des rayons du Soleil[20].
Newton vs Descartes
La « philosophie » d'Isaac Newton (le « système anglais ») est propagée en France par Émilie du Châtelet (1706-1749), François Jacquier (1717-1788), Thomas Leseur (1703-1770), Roger Joseph Boscovich (1711-1787), Alexis Claude Clairaut (1713-1765), Colin Maclaurin, Pierre Louis Moreau de Maupertuis (1698-1759). Elle fait polémique et voit se dresser contre elle les partisans de René Descartes et de la théorie des tourbillons: les cartésiens donc, mais aussi les malebranchistes et les jansénistes. Voltaire (1694-1778), baptisé et « confirmé » dans la religion Newtonienne par Maupertuis, fait allusion à cette polémique dans la 14e de ses Lettres Philosophiques en 1734 : « Un Français qui arrive à Londres trouve les choses bien changées en Philosophie comme dans tout le reste. Il a laissé le monde plein ; il le trouve vide. À Paris, on voit l'univers composé de tourbillons de matière subtile ; à Londres, on ne voit rien de cela. Chez nous, c'est la pression de la Lune qui cause le flux des marées ; chez les Anglais, c'est la mer qui gravite vers la Lune […] À Paris, vous figurez la Terre faite comme un melon, à Londres elle est aplatie des deux côtés. », simplification d'essayiste car Huygens, cartésien, croyait lui aussi que la terre était aplatie aux pôles[21]:
- Conséquence de la gravitation universelle, Newton prévoit un aplatissement du globe terrestre aux pôles, confirmée par la différence de gravité détectée par Jean Richer en 1672. Cependant, ces données sont contestées par Jacques Cassini. Il s'ensuit les expéditions géodésiques françaises des années 1730 dont le résultat des mesures faites à cette occasion en Suède et au Pérou confirment que la Terre était aplatie et non allongée, de là une nouvelle levée de bouclier. Les aspects techniques de cette entreprise requièrent la collaboration et l'expertise de disciplines aussi variées que la géographie, la géodésie, la cartographie, l'astronomie et les mathématiques, disciplines qui vont sortir de l'expérience transformées et rapprochées[22].
- Aristote avait refusé l'idée d'un vide physique. On voit chez Galilée que la question du vide constitue une condition de pureté à laquelle on tend en raisonnant à la limite (à partir d'expériences de ralentissement en divers milieux) sans parvenir dans l'absolu; c'est-à-dire un milieu expérimental relativement vide dans lequel on s'approche des conditions « idéales » d'étude de la pesanteur terrestre affectant les corps indépendamment de leur densité et égalisant leur temps de chute « loin de tout facteur particularisant ». Galilée est d'autre part bien familiarisé avec la pesanteur de l'air et enseigne dans ses Dialogues deux moyens de la démontrer et de la mesurer, mais il ne va pas plus loin et l'honneur de découvrir la pression de l'atmosphère est réservée à son disciple Evangelista Torricelli. Là où Pascal, certainement plus empiriste, croit que l'expérience de Torricelli tranche en faveur du vide à l'intérieur du tube renversé, René Descartes (1596-1650) introduit la notion de materia subtilis qui, non perceptible, remplit le haut du tube, « matière imperceptible, inouïe et inconnue à tous les sens ». En face des vacuistes (du latin vacuum, vide), les plénistes ne baissent pas les bras. Peuvent être comptés parmi les plénistes, à côté de penseurs qui admettent des concepts purs et indépendants de toute expérience sensible, de tradition cartésienne, des penseurs plus proches de l'aristotélisme, tel Thomas Hobbes, qui très tôt est conscient que la perception a ses limites « de sorte que l'hypothèse d'une réalité inaccessible aux sens ne le heurte pas par principe et qu'il n'attaque pas la notion même de matière subtile dans ses travaux d'optique[23]. Newton au départ pléniste établit la certitude du vide, de par l'universalité des déductions qu'elle autorise. Les trois Livres des Philosophiae naturalis principia mathematica sont consacrés, sur la base des définitions et lois du mouvement: le premier aux mouvements des corps, abstraction faite du milieu (air, eau, etc.); le second, aux mouvements des corps en des milieux résistants; le troisième aux mouvements des corps qui se déplacent en des milieux non-résistants. Ceci permet d'établir, au troisième Livre, que les corps célestes, n'éprouvant aucune résistance de leur milieu - comme les observations astronomiques de l'époque l'attestent (celles de Nicolas Copernic (1473-1543), Johannes Kepler (1571-1630), Tycho Brahe (1546-1601), etc. - et ne pouvant donc être mus par des tourbillons de « matière très subtile », doivent obéir à d'autres lois que celles fixées par Descartes. D'où le rejet de la théorie des tourbillons, d'où la théorie de la gravitation universelle produisant un nouveau « système du monde »[19].
La mécanique mathématique et analytique
Cette controverse sur la figure de la Terre est révélatrice d'un mode nouveau de discussion et de preuve. On cherche des confirmations expérimentales détaillées, on discute la fiabilité des appareils et on tient compte des limites de la précision accessible. Les Académies commencent à jouer un rôle très officiel, avec les moyens puissants d'une science d’État. Les mathématiques s'enrichissent considérablement: la différence est sensible entre les raisonnements encore assez simples de Maupertuis sur les figures d'équilibre dans son Discours de 1732 et les raffinements de Clairaut dans sa Théorie de la figure de la terre de 1743. Les marées donnent l'occasion d'un autre assaut de la nouvelle mathématique, lors du prix de l'Académie des Sciences pour 1740. Les mémoires de Daniel Bernoulli et Leonhard Euler sont les premières études approfondies d'un cas de gravitation en termes analytiques et différentiels. Ironie du sort : l'analyse leibnizienne s'applique et s'enrichit pour confirmer le système newtonien. Progressivement la discussion passe dans le camp des "géomètres", des mathématiciens professionnels. Ainsi, lors de la crise survenue en 1747 à propos du mouvement de l'apogée lunaire, une sorte de tri s'opère entre les philosophes "non géomètres" comme dit Clairaut, et les véritables experts capables de décider. Lorsque Newton se trouva dans ce cas confirmé avec éclat, Clairaut tint à marquer que les objections de "quelques newtoniens non géomètres" n'étaient pas d'un grand poids dans la discussion. Dès lors Buffon qui s'était mêlé de l'affaire, ne s'occupa plus de physique mathématique. Diderot et Voltaire eux aussi étaient retournés aux Belles Lettres, le temps des newtoniens philosophes était passé[21].
Jean Bernoulli (1667-1748) et Daniel Bernoulli (1700-1782), ont fait les premiers très petits pas en direction de la mécanique analytique, c'est-à-dire une méthode basée sur l'application du calcul intégral et différentiel. La vraie percée vers la mécanique céleste analytique sera faite seulement par Alexis Claude Clairaut célèbre pour son fameux calcul de la date précise du retour de la Comète de Halley (1747). Après Clairaut et dans les 100 années qui suivent les Principia viennent Leonhard Euler (1707-1783), Jean le Rond D'Alembert (1717-1783), Jean-Henri Lambert (1728-1777), Joseph-Louis Lagrange (1736 - 1813) et sa Mécanique analytique de 1788 et Pierre-Simon de Laplace (1749-1827)[24]. Léonard Euler élabore les méthode de résolution des problèmes de la dynamique du point et du corps solide, basées sur la mise en équation et l'intégration des équations différentielles correspondantes. d'Alembert propose le principe de résolution des problèmes de dynamique et Lagrange élabore la méthode générale de résolution analytique des problèmes de dynamique sur la base du Principe de D'Alembert et du principe des déplacements virtuels. Ces méthodes analytiques de résolution des problèmes reçoivent par la suite une application générale en mécanique[25].
La mécanique classique
Le développement ultérieur de la science a montré que pour des vitesse de l'ordre de celle de la lumière, le mouvement des corps est soumis aux lois de la mécanique relativiste, et le mouvement des micro-éléments aux lois de la mécanique quantique. Ces découvertes n'ont toutefois fait que préciser le domaine d'application de la mécanique classique et confirmer la justesse de ses lois pour le mouvement de tous les corps autres que les particules élémentaires pour des vitesses n'approchant pas de celle de la lumière[25]. Reposant sur les acquis de Galilée puis de Newton, la mécanique classique s'appuie également sur les avancées introduites avec la mécanique analytique. La notion de lagrangien est au cœur de cette science.
On appelle mécanique ![]() au sens général du terme la science ayant pour objet la résolution de tous les problèmes liés à l'étude du mouvement ou de l'équilibre de tels ou tels corps matériel et leurs interactions. La mécanique rationnelle constitue la partie de la mécanique qui étudie les lois générales des mouvements, de l'équilibre et des interactions des corps matériels. Le champ d'application de celle-ci concerne les lois valables aussi bien pour le mouvement de la Terre autour du Soleil, celui d'une fusée
au sens général du terme la science ayant pour objet la résolution de tous les problèmes liés à l'étude du mouvement ou de l'équilibre de tels ou tels corps matériel et leurs interactions. La mécanique rationnelle constitue la partie de la mécanique qui étudie les lois générales des mouvements, de l'équilibre et des interactions des corps matériels. Le champ d'application de celle-ci concerne les lois valables aussi bien pour le mouvement de la Terre autour du Soleil, celui d'une fusée ![]() , ou d'un obus, etc.. L'autre partie de la mécanique comprend les différentes branches de la mécanique dite appliquée concernant l'élaboration de projets et les calculs de toutes sortes de constructions, de moteurs, de mécanismes, de machines et de leurs organes, disciplines basées sur la mécanique rationnelle.
, ou d'un obus, etc.. L'autre partie de la mécanique comprend les différentes branches de la mécanique dite appliquée concernant l'élaboration de projets et les calculs de toutes sortes de constructions, de moteurs, de mécanismes, de machines et de leurs organes, disciplines basées sur la mécanique rationnelle.
L'étude de la mécanique se répartit de manière générale en trois parties suivant le problème considéré: La statique, la cinématique et la dynamique[25].
- La statique étudie les lois de la composition des forces et les conditions d'équilibre des corps matériels soumis à l'action des forces; La statique du corps solides étudie essentiellement deux problèmes principaux: « Composition des forces et réduction d'un système de force appliquées à un corps solide à sa plus simple expression », « détermination des conditions d'équilibre des systèmes de forces agissant sur un corps solide ». Les problèmes de statique peuvent se résoudre par des constructions géométriques et graphiques appropriées (Statique graphique, voir aussi la catégorie correspondante), soit par des procédés numériques analytique (mécanique analytique).
- la cinématique étudie les propriétés géométriques du mouvement des corps sans tenir compte de leur inertie (masse) et des forces agissant sur eux. Le mouvement des corps s'effectuant dans l'espace et dans le temps, la mécanique pratique, suppose l'espace euclidien tridimensionnel, et le temps considéré universel. La cinématique s'attache à la recherche des formes mathématiques d'expression du mouvement des points ou des corps. La cinématique est une introduction à la dynamique, mais elle a aussi une signification pratique propre dans le contexte de l'industrie mécanique, qui fait appel à elle pour l'étude de la transmission des mouvements par exemple, et elle est par ailleurs devenue une discipline propre, début XIXe siècle, sous l'impulsion de celle-ci.
- la dynamique étudie les lois des mouvements des corps matériels soumis à l'action des forces. On tient compte aussi bien des forces agissantes sur le corps que de l'inertie. Un corps en mouvement subit l'actions conjuguée de différentes forces dont certaines sont constantes (la pesanteur peut être considérée comme telle) et d'autres dont les modules et les directions varient pendant le mouvements. Afin de ne pas tenir compte dans un premier temps de l'influence des dimensions des corps et la distribution des masses, la mécanique introduit la notion de point matériel.
Mécanique rationnelle
Suivant la nature de l'objet étudié, on divise la mécanique rationnelle en :
- Mécanique du point matériel
- Mécanique des corps solides
- Mécanique des corps à masse variable
- Mécanique des corps déformables
- Mécanique des fluides
Mécanique des fluides
Le Livre II des Principia Mathematica de Newton qui traite des mouvements des corps en des milieux résistants, ne laisse aucun acquis scientifique substantiel. Cependant, selon Clifford Truesdell, les travaux de Newton ont fourni à ces deux disciplines un programme qui a été suivi pendant cinquante ans[24]. Il faut attendre les travaux de Alexis Claude Clairaut (1713-1765) et Jean le Rond D'Alembert (1717-1783) pour que commencent à s'établir les lois de la mécanique des fluides[19].
L’étude de la mécanique des fluides remonte au moins à l’époque de la Grèce antique avec Archimède qui fut à l’origine de la statique des fluides. Si Simon Stevin (1548-1620) découvrit les grands principes de l'hydrostatique, complétant ainsi l'œuvre d'Archimède, le Brugeois ne parvint pas cependant à les présenter sous une forme suffisamment belle et ordonnée; ce fut l'œuvre de Pascal de donner à ces découvertes une forme irréprochable. On peut dire que, si Stevin découvrit le paradoxe hydrostatique et le principe de l'égalité de pression dans un liquide, ce fut Blaise Pascal qui, dans son « Récit de la grande expérience de l'équilibre des liqueurs » de 1648, donna le premier un exposé homogène et bien ordonné de ces principes fondamentaux de l'hydrostatique[26]. Les manifestations du paradoxe hydrostatique sont utilisées dans l'enseignement du phénomène. L'un des expériences les plus connues est le crève-tonneau de Pascal.
La mécanique moderne
Au début du XXe siècle, et alors que la mécanique classique semble être un édifice inébranlable, deux révolutions viennent la remettre radicalement en cause, qui donneront naissance pour l'une à la mécanique quantique, pour l'autre à la mécanique relativiste.
Notes et références
- Il est, selon le dictionnaire d'Alain Rey, attesté depuis 1268 comme adjectif caractérisant « les métiers comportant l'usage d'instrument et l'action de la main ». Il est substantivé à partir du XIIIe siècle pour désigner les ouvriers manuels artisans.
- Fleury Philippe. Le De architectura et les traités de mécanique ancienne. In: Le projet de Vitruve. Objet, destinataires et réception du De architectura Actes du colloque international de Rome (26-27 mars 1993) Rome : École Française de Rome, 1994. pp. 187-212. (Publications de l'École française de Rome, 192) [www.persee.fr/doc/efr_0000-0000_1994_act_192_1_4390 lire en ligne]
- Alain Rey, Dictionnaire historique de la langue française, 1992, pp. 1210-1211
- L'encyclopédie, sur wikisource
- Costabel Pierre. La mécanique dans l'Encyclopédie . In: Revue d'histoire des sciences et de leurs applications, tome 4, n°3-4, 1951. pp. 267-293. Lire en ligne
- Raepsaet Georges. Transport de tambours de colonnes du Pentélique à Éleusis au IVe siècle avant notre ère. In: L'antiquité classique, Tome 53, 1984. pp. 101-136. Lire en ligne
- Mugler Charles. Archimède répliquant à Aristote. In: Revue des Études Grecques, tome 64, fascicule 299-301, Janvier-juin 1951. pp. 59-81. Lire en ligne
- Dubarle Dominique. La méthode scientifique de Galilée. In: Revue d'histoire des sciences et de leurs applications, tome 18, n°2, 1965. pp. 161-192. Lire en ligne
- Gille Bertrand. Histoire des techniques. In: École pratique des hautes études. 4e section, Sciences historiques et philologiques. Annuaire 1974-1975. 1975. pp. 697-728. [www.persee.fr/doc/ephe_0000-0001_1974_num_1_1_6036 Lire en ligne]
- Van Steenberghen Fernand. L'organisation des études au moyen âge et ses répercussions sur le mouvement philosophique. In: Revue Philosophique de Louvain. Troisième série, tome 52, n°36, 1954. pp. 572-592. DOI : 10.3406/phlou.1954.4516 Lire en ligne
- Wilbur Applebaum. Encyclopedia of the Scientific Revolution: From Copernicus to Newton. Routledge, 16 déc. 2003
- In Librum Boethii De Trinitate Pars3 Qu.5 Art.3. In Librum Boethii De Trinitate (Sancti Thomae Aquinatis): textus a B. Decker editus, 2a ed., Leiden 1959. Lire en ligne
- Pierre Duhem. Les Origines de la statique, 1903, Lire en ligne
- Charles Thurot. Recherches historiques sur le principe d'Archimède. Librairie Académique, 1869. Lire en ligne
- Notice historique sur Simon Stevin, suivie des notices biographiques des hommes illustres dont les statues, bustes et médaillons décorent la Grand Place de la ville de Bruges, à l’occasion des fêtes inaugurales de la statue de Simon Stevin. Bogaert, 1846
- Demonstratio proportionum motuum localium contra Aristotilem, Dans Koyré
- Koyré A. Le De Motu Gravium de Galilée. De l'expérience imaginaire et de son abus.. In: Revue d'histoire des sciences et de leurs applications, tome 13, n°3, 1960. pp. 197-245. Lire en ligne
- Barthelemy Georges. Newton découvreur du poids de toutes choses / Newton as discoverer of the weight of all things. In: Revue d'histoire des sciences, tome 57, no 1, 2004. p. 135-159. lire en ligne
- Biarnais Marie-Françoise. Les « Principia Mathematica » : défi aux « Principes » cartésiens ou réalité ? In: Revue Philosophique de Louvain, quatrième série, tome 86, n°72, 1988. pp. 440-466. Lire en ligne.
- Taton René. Sur la « comète de Halley » et son « retour » en 1986. In: Revue d'histoire des sciences, tome 39, n°4, 1986. pp. 289-300. Lire en ligne
- De Gandt Francois. La réception de Newton : philosophes et géomètres.. In: Revue du Nord, tome 77, n°312, Octobre-décembre 1995. pp. 845-857. DOI : 10.3406/rnord.1995.5052 [www.persee.fr/doc/rnord_0035-2624_1995_num_77_312_5052 Lire en ligne]
- Iliffe Rob. Ce que Newton connut sans sortir de chez lui : Maupertuis et la forme de la terre dans les années 1730. In: Histoire & Mesure, 1993 volume 8 - n°3-4. La mesure de la terre. pp. 355-386. Lire en ligne
- Bernhardt Jean. La question du vide chez Hobbes. In: Revue d'histoire des sciences, tome 46, n°2-3, 1993. pp. 225-232. Lire en ligne
- Speiser David. Le «Horologium Oscillatorium» de Huygens et les «Principia». In: Revue Philosophique de Louvain. Quatrième série, tome 86, n°72, 1988. pp. 485-504. Lire en ligne
- S. Targ. Éléments de mécanique rationnelle. Édition Mir. Moscou 1966
- Brunet Pierre. Georges Leboucq, André Vésale ; Robert Depau, Simon Slevin ; Lucien Godeaux, Esquisse d'une histoire des mathématiques en Belgique ; E. Dupréel, Adolphe Ouételel, pages choisies et commentées ; Jean Pelseneer, Zénobe Gramme ; Marcel Florkin, Léon Frédéricq et les débuts de la physiologie en Belgique ; Raymond Lebègue, Les correspondants de Peiresc dans les anciens Pays-Bas. In: Revue d'histoire des sciences et de leurs applications, tome 1, n°1, 1947. pp. 82-86. Lire en ligne
Voir aussi
Articles connexes
Liens externes
- Portail du génie mécanique
- Portail de la physique
- Portail de l’histoire des sciences