Géométrie symplectique

L'adjectif symplectique fut introduit par le mathématicien Hermann Weyl (1885 – 1955) pour désigner le groupe symplectique ${\displaystyle Sp(2n)}$, le groupe des automorphismes linéaires réels de ${\displaystyle C^{n}}$ conjuguant la multiplication par i à elle-même. Ce groupe était appelé « groupe du linéaire complexe » et une confusion était possible avec le groupe des automorphismes linéaires complexes. Hermann Weyl justifie son choix :

« The name “complex group” formerly advocated by me in allusion to line complexes, as these are defined by the vanishing of antisymmetric bilinear forms, has become more and more embarrassing through collision with the word “complex” in the connotation of complex number. I therefore propose to replace it by the corresponding Greek adjective “symplectic”.

Le nom de « groupe complexe » que j'avais précédemment proposé, par allusion aux complexes de droites (car ils sont définis par l'annulation de formes bilinéaires antisymétriques), est devenu de plus en plus embarrassant à cause des confusions possibles avec l'usage de « complexe » dans l'expression « nombre complexe ». Je propose donc de le remplacer par l'adjectif grec correspondant « symplectique ». »

— Hermann Weyl, The classical Groups. Their Invariants and Representations

Plus exactement, l'adjectif « symplectique » est fondé sur la racine grecque συµπλεκτικoς, traduction de la racine latine de complexus. La racine latine a donné le nom de complexité d'où dérive « nombre complexe », ce nom latin traduit l'idée d'entrelacement. En histoire naturelle, l'adjectif symplectique désigne « être entrelacé avec un autre corps ».

Par extension, l'adjectif symplectique a été utilisé dans l'appellation de forme symplectique et de variété symplectique (voir définitions ci-dessous).

Le concept de structure symplectique est bien antérieur à l'introduction de la terminologie actuelle. Il émerge dans les années 1808 à 1810 dans les travaux de Joseph-Louis Lagrange et de son élève Siméon Denis Poisson sur la trajectoire des planètes[2]. Ils entreprennent d'expliquer la variation lente des paramètres orbitaux des planètes du système solaire en tenant compte des interactions mutuelles de ces corps. En utilisant la terminologie actuelle, ils introduisent à cette occasion la forme symplectique associée à la variété décrivant les états du système et une opération fondamentale sur les fonctions : le crochet de Poisson.

Le cadre de la géométrie symplectique a permis de donner un nouveau regard sur la mécanique classique. Elle permet l'étude du comportement global d'un système mécanique, en traitant les symétries et les conséquences, et aborde des questions qualitatives associées comme l'existence de trajectoires périodiques ou le caractère chaotique ou stable d'une évolution.

En mécanique, la position d'un ensemble de points matériels ou plus généralement d'un objet en mouvement est traditionnellement repérée par un certain nombre de coordonnées curvilignes ${\displaystyle q=(q_{1},\dots ,q_{n})}$. Le nombre ${\displaystyle n}$ est appelé nombre de degrés de liberté du système. Par exemple, un pendule astreint à rester dans un plan est repéré par un seul paramètre ${\displaystyle q_{1}}$, à savoir l'angle que fait sa tige avec la verticale définie par le champ de gravité. Les positions occupées par deux masses ponctuelles en interaction (par exemple une planète et une étoile) sont repérées par six paramètres, trois pour chaque masse. L'ensemble des différentes valeurs ${\displaystyle (q_{1},\dots ,q_{n})}$ que les coordonnées peuvent prendre dans toutes les positions possibles du système est appelé espace de configuration. Les lois de Newton de la mécanique affirment (entre autres choses) qu'un système mécanique évolue d'une façon déterministe qui peut être prévue si on connait la position et la vitesse d'un point à l'instant initial.

Espace des phases du pendule simple.

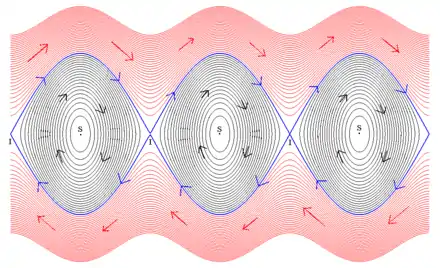
Pour prendre en compte les vitesses, il est nécessaire d'ajouter aux coordonnées de position ${\displaystyle n}$ de nouvelles variables ${\displaystyle p=(p_{1},\dots ,p_{n})}$. Dans le premier exemple, ${\displaystyle p_{1}}$ serait la vitesse angulaire du pendule et dans le deuxième, on aurait les composantes de la vitesse des deux planètes. L'ensemble des valeurs ${\displaystyle (q_{1},p_{1},\dots ,q_{n},p_{n})}$ que peuvent prendre les différents paramètres est appelé espace des phases du système. Les trajectoires du système se tracent dans cet espace.

Bien sûr, il n'est en général pas possible de calculer explicitement toutes les trajectoires possibles et même un tel calcul ne donne pas forcément une bonne idée globale du comportement du système étudié. Pour comprendre ce comportement, on peut essayer de suivre le déplacement d'un sous-ensemble de l'espace des phases ; on a alors accès à des informations globales et qualitatives.

Dans toute la suite, on suppose que le système évolue en suivant les lois de la mécanique de Newton pour des forces dérivant d'un potentiel (ce qui signifie en simplifiant qu'il n'y a pas de frottements).

On peut se demander quel type de géométrie est adapté à cette étude des trajectoires dans l'espace des phases. La géométrie euclidienne est la plus familière mais elle n'est pas adaptée car les droites ne sont pas conservées lors de l'évolution d'un système mécanique. Ainsi, dans l'exemple du pendule simple, on constate que si l'on part de configurations alignées, cette propriété se perd en route. Il y a pire : un segment de droite n'est même pas envoyé sur une courbe de même longueur. Dans la suite, on verra que la géométrie pertinente est la géométrie symplectique.

Le théorème de Liouville affirme que lorsqu'un système mécanique évolue, le volume de toute partie de l'espace des phases est préservé. Voici comment on définit le volume d'une partie de l'espace des phases qui est de dimension ${\displaystyle 2n}$. Si la partie est définie par les conditions :

${\displaystyle q_{1}^{0}\leq q_{1}\leq q_{1}^{1},p_{1}^{0}\leq p_{1}\leq p_{1}^{1},\dots ,q_{n}^{0}\leq q_{n}\leq q_{n}^{1},p_{n}^{0}\leq p_{n}\leq p_{n}^{1}}$

alors le volume est

${\displaystyle (q_{1}^{1}-q_{1}^{0})(p_{1}^{1}-p_{1}^{0})\dots (q_{n}^{1}-q_{n}^{0})(p_{n}^{1}-p_{n}^{0}).}$

Dans le cas où ${\displaystyle n=1}$ on retrouve la définition de l'aire d'un rectangle. Si la partie dont on veut calculer le volume est plus compliquée, on la découpe en un très grand nombre de parties telles que plus haut et on fait la somme des volumes. Lorsque le nombre de rectangle tend vers l'infini et que leur réunion tend vers la partie initiale on trouve le volume.

Ainsi dans le cas du pendule simple, on a conservation de l'aire de toute partie de l'espace des phases que l'on suit lors de l'évolution du système.

Le théorème de Liouville affirme que l'évolution d'un système mécanique préserve le volume dans l'espace des phases.

On peut donc penser que la structure géométrique de l'espace des phases est celle du volume des objets mais on va voir dans le paragraphe suivant qu'il existe une géométrie plus subtile.

Le théorème de Poincaré est un raffinement du théorème de Liouville. Pour l'énoncer il faut introduire quelques notations. Pour tout ${\displaystyle i}$ compris entre 1 et ${\displaystyle n}$, on note ${\displaystyle \pi _{i}}$ la projection de l'espace des phases sur le plan des ${\displaystyle (q_{i},p_{i})}$. C'est donc la fonction qui à ${\displaystyle (q_{1},p_{1},\dots ,q_{n},p_{n})}$ associe ${\displaystyle (q_{i},p_{i})}$.

Le théorème de Poincaré affirme que pour toute surface ${\displaystyle S}$ dans l'espace des phases, la somme des aires des projections ${\displaystyle \pi _{i}(S)}$ est conservée par l'évolution du système.

Une structure symplectique sur un ensemble est un mécanisme d'attribution d'un nombre à toute surface dans l'ensemble et qui vérifie certaines conditions sur lesquelles on reviendra plus loin. Le fait d'associer à chaque surface ${\displaystyle S}$ de l'espace des phases la somme des aires de ses projections ${\displaystyle \pi _{i}(S)}$ est un exemple de telle structure qu'on appelle structure symplectique canonique de l'espace des phases.

Le théorème de Poincaré affirme donc que l'évolution d'un système mécanique préserve la structure symplectique canonique de l'espace des phases.

On peut montrer que le théorème de Poincaré implique celui de Liouville.

Pendant très longtemps, personne n'a su si le théorème de Poincaré permettait d'avoir vraiment plus d'information sur l'évolution des formes dans l'espace des phases que le théorème de Liouville. Enfin, en 1985, Mikhaïl Gromov a démontré le théorème suivant : pour tout système mécanique à ${\displaystyle n}$ degrés de liberté, la boule : ${\displaystyle B=\{(q_{1},p_{1},\dots ,q_{n},p_{n});q_{1}^{2}+p_{1}^{2}+\cdots +q_{n}^{2}+p_{n}^{2}\leqslant 1\}}$ ne peut jamais évoluer en un ensemble dont tous les points vérifient : ${\displaystyle q_{i}^{2}+p_{i}^{2}\leqslant r^{2}}$ pour un ${\displaystyle r}$ strictement plus petit que 1.

Or une telle évolution serait possible si seul le théorème de Liouville était vrai et pas le théorème de Poincaré. Ce théorème de Gromov est un théorème difficile et qui a de nombreuses conséquences, il a révolutionné le domaine de la géométrie symplectique.

La présence de symétries dans un système mécanique a toujours pour conséquence la conservation de certaines quantités calculées à partir des positions et vitesses des objets étudiés. Ainsi lorsqu'un système est invariant par translation dans une direction, la quantité de mouvement dans cette direction est conservée. Lorsque le système est invariant par rotation autour d'un axe, le moment cinétique par rapport à cet axe est conservé.

Dans la formulation newtonienne de la mécanique classique, il semble impossible d'énoncer un théorème général qui engloberait les exemples cités ainsi que des situations possédant des symétries plus compliquées.

Le théorème de Noether affirme que dès que l'on a un groupe à un paramètre de transformations qui préserve un système mécanique il existe une quantité conservée lors de l'évolution de ce système. En fait l'énoncé complet donne une formule pour cette quantité en fonction des transformations et du système considérés.

Dans la formulation lagrangienne de la mécanique on peut démontrer ce théorème en une dizaine de lignes. Dans la formulation hamiltonienne en termes de géométrie symplectique la démonstration ne fait qu'une ligne et l'énoncé se généralise au cas de groupe de transformations à un nombre quelconque de paramètres qui ne commutent pas nécessairement entre elles. Le nombre de quantités conservées est alors égal au nombre de paramètres du groupe de transformations.

Une des conséquences de l'existence de quantités conservées est qu'elle contraint le système mécanique étudié à rester dans certaines régions de l'espace des phases définies par les conditions initiales.

Lorsqu'on a autant de quantités conservées que de degrés de liberté on dit que le système mécanique est intégrable et la situation devient très simple, c'est ce qu'affirme le théorème d'Arnold-Liouville : pour presque toute énergie de départ il existe des coordonnées ${\displaystyle (I_{1},\dots ,I_{n},\theta _{1},\dots ,\theta _{n})}$ et des nombres ${\displaystyle \omega _{i}(I_{1},\dots ,I_{n})}$ tels que

Bien sûr la plupart des systèmes mécaniques ne sont pas intégrables mais certains sont proches d'être intégrables, on peut alors essayer de comprendre dans quelle mesure leur comportement s'éloigne de celui d'un système intégrable, c'est l'objet de la théorie des perturbations qui fait elle aussi un grand usage de la structure symplectique des espaces de phases.

Des connaissances élémentaires en géométrie différentielle sont nécessaires pour aborder les aspects techniques de la géométrie symplectique. L'introduction ici présentée donne un entr'aperçu des résultats fondamentaux qui se veut abordable.

La géométrie symplectique partage de nombreux points communs avec la géométrie de Riemann, qui étudie les variétés différentielles dotées de tenseurs bilinéaires non dégénérés symétriques. Par contre, les variétés symplectiques n'ont pas d'invariants locaux telle que la courbure. C'est une conséquence du théorème de Darboux qui établit que deux variétés symplectiques de même dimension sont localement isomorphes. La question de savoir quelles variétés admettent des structures symplectiques n'est pas encore complètement résolue.

Chaque variété de Kähler est également une variété symplectique. Au cours des années 1970, les experts du domaine étaient incertains quant à la question de savoir si des variétés symplectiques compactes autres que celles de Kähler existaient, mais depuis plusieurs exemples ont pu être construits (le premier est dû à William Thurston).

La plupart des variétés symplectiques ne sont pas de Kähler et n'ont donc pas de structure complexe intégrable compatible avec la forme symplectique. Mikhaïl Gromov a remarqué cependant que les variétés symplectiques possèdent de nombreuses structures quasi-complexes qui vérifient tous les axiomes d'une variété complexe à l'exception du fait que les fonctions de transition n'y sont pas holomorphes.

Gromov développa le fait qu'il existe de telles structures pour fonder une théorie des courbes pseudoholomorphes, qui permit de grandes avancées dans la recherche géométrique symplectique, et notamment la découverte d'une classe d'invariants connus sous le nom d'invariants de Gromov-Witten, en coopération avec Edward Witten, qui jouent un rôle clé dans la théorie des cordes.

La géométrie euclidienne concerne les espaces affines euclidiens E : à ces derniers sont associées une distance naturelle, appelée distance euclidienne, unique invariant pour l'action diagonale du groupe des isométries affines de E sur E², et une notion d'angle. Les distances et angles définis par un ensemble de points de E sont préservés sous l'action d'une isométrie.

En oubliant la notion de distance, il est loisible de s'intéresser uniquement au volume euclidien. Un isomorphisme linéaire affine préservant le volume est de déterminant +1 ou -1. Malheureusement, en dimension n, on perd ainsi toute information sur les configurations d'au plus n-1 points.

La géométrie symplectique linéaire apparaît comme une géométrie intermédiaire, dans laquelle on perd la notion de distance, tout en conservant une notion d'aire orientée, et donc un invariant associé à 3 points. À trois points A, B et C d'un espace vectoriel réel E doit être associée une aire a(ABC). Pour des raisons d'additivité et de monotonicité des aires, cette quantité doit s'écrire :

${\displaystyle a(ABC)=\omega (AB,AC)}$,

où ${\displaystyle \omega :E^{2}\rightarrow E}$ est une forme bilinéaire. Comme une transposition sur les points A, B, C change l'orientation du triangle ABC, la forme ${\displaystyle \omega }$ doit être antisymétrique au sens où, pour tous vecteurs u et v :

${\displaystyle \omega (u,v)=-\omega (v,u)}$.

Cette forme est dite non dégénérée lorsque, pour tout vecteur ${\displaystyle u\neq 0}$, il existe un vecteur v vérifiant : ${\displaystyle \omega (u,v)\neq 0}$. Par définition, une forme symplectique sur E désigne une forme bilinéaire antisymétrique non dégénérée. Une telle forme est unique à isomorphisme linéaire près ; et son existence implique que la dimension de E soit paire, disons 2n. Le modèle standard est l'espace Cⁿ regardé comme espace vectoriel réel, avec comme forme symplectique la partie imaginaire de la métrique hermitienne standard.

Un isomorphisme linéaire ou affine de E est dit symplectique lorsqu'il préserve la forme symplectique ${\displaystyle \omega }$. L'ensemble des isomorphismes linéaires symplectiques de Cⁿ forme un groupe, appelé le groupe symplectique, noté Sp(n) ou Sp(2n) suivant les auteurs. C'est un groupe de Lie classique connexe non compact de dimension n(n-1)/2. Il contient le groupe unitaire U(n) comme rétract fort par déformation : ces deux groupes ont donc le même type d'homotopie.

La classification des ellipsoïdes dans un espace euclidien de dimension 2n modulo les isométries est donnée par 2n invariants, qui sont leurs diamètres respectifs. Par opposition, comme observé par Hofer et Zehnder[3], la classification des ellipsoïdes d'un espace symplectique modulo les applications affines symplectiques est donné par n invariants.

Les variétés différentielles s'obtiennent par des recollements d'ouverts d'espaces vectoriels réels de dimension finie suivant des difféomorphismes. Un intérêt porté sur des structures particulières peut conduire à imposer des restrictions sur la nature de ces recollements.

L'objet d'étude de la géométrie symplectique est les 2-formes différentielles fermées non dégénérées. Une telle forme différentielle est appelée forme symplectique. Sur une variété différentielle M, on se donne une forme antilinéaire non dégénérée ${\displaystyle \omega _{x}}$, et on demande que la collection ${\displaystyle \omega =\{\omega _{x}\}_{x\in M}}$ ait une certaine régularité en x. L'application ${\displaystyle \omega :x\mapsto \omega _{x}}$ est un exemple de 2-forme différentielle, qu'on exige fermée : tous champs de vecteurs X, Y, et Z vérifient :

${\displaystyle X\cdot \omega (Y,Z)+Y\cdot \omega (Z,X)+Z\cdot \omega (X,Y)=\omega ([X,Y],Z)+\omega ([Y,Z],X)+\omega ([Z,X],Y)}$.

Gaston Darboux.

Une variété munie d'une forme symplectique est appelée variété symplectique. Une fois les objets d'étude définis, on a coutume de s'intéresser aux relations qu'ils peuvent entretenir entre eux. Un difféomorphisme ${\displaystyle f:M\rightarrow N}$ s'appelle difféomorphisme symplectique lorsque f préserve les formes symplectiques ${\displaystyle \omega }$. De manière plus explicite, la différentielle ${\displaystyle df(x):(T_{x}M,\omega _{x})\rightarrow (T_{x}N,\eta _{x})}$ est un isomorphisme linéaire symplectique. Le lecteur mal à l'aise avec la géométrie différentielle comprendra les choses ainsi : au premier ordre, f est un isomorphisme symplectique linéaire.

L'ensemble des difféomorphismes symplectiques de ${\displaystyle (M,\omega )}$ forme un groupe, appelé groupe des symplectomorphismes, et noté ${\displaystyle Symp(M,\omega )}$. Son étude a un intérêt de premier plan.

L'un des principaux résultats élémentaires de la géométrie symplectique est le théorème de Darboux : localement, deux variétés symplectiques de même dimension sont isomorphes. Dit autrement, aucun invariant local n'existe. Sur ce point, et pas le moindre, la géométrie symplectique s'oppose complètement à la géométrie riemannienne :

• En géométrie riemannienne, l'existence d'invariants de classe C² se traduit par un groupe d'isométries de dimension finie et une quantité infinie de classes d'équivalence de métriques riemanniennes ;
• En géométrie symplectique, l'inexistence d'invariants locaux au contraire donne un groupe de dimension infinie de difféomorphismes symplectiques et un ensemble « discret » de classes d'équivalence de formes symplectiques.

Cette dichotomie résume bien l'opposition entre la souplesse de la géométrie riemannienne contre la rigidité de la géométrie symplectique. Cette rigidité se retrouve à bien d'autres niveaux (rigidité des symplectomorphismes, théorème de rigidité de Gromov…).

Les espaces de phases étudiés jusqu'à maintenant étaient assez simples car nous étions partis d'espaces de configurations assez simples. Cependant, dans l'exemple du pendule simple, il eut été plus logique de considérer que la variable ${\displaystyle q_{1}}$ vivait dans un cercle et pas dans une droite. Plus généralement, on peut imaginer des espaces de configuration arbitrairement compliqués, par exemple si un point est astreint à se déplacer sur une surface ayant une forme sophistiquée.

Quelle que soit la complexité de l'espace de configuration on peut toujours lui associer un espace des phases appelé fibré cotangent de l'espace de configuration et qui est toujours muni d'une structure symplectique canonique. Les théorèmes de Liouville, Poincaré, Noether et Liouville-Arnold restent vrais et on peut donner des analogues du théorème de Gromov dans ce cadre plus général.

On peut vouloir aller plus loin dans la généralisation et étudier tous les espaces munis d'une structure symplectique. Pour cela il faut revenir un peu plus en détail sur la définition d'une structure symplectique. À partir de maintenant on considère une variété ${\displaystyle M}$ de dimension ${\displaystyle 2n}$, c'est-à-dire un ensemble qui peut localement être paramétré par ${\displaystyle 2n}$ nombres. Comme expliqué plus haut, une structure symplectique sur ${\displaystyle M}$ est une application qui, à toute surface dans ${\displaystyle M}$, associe un nombre et qui vérifie en plus deux propriétés. La première est que cette structure doit permettre d'associer un volume à toute partie de dimension ${\displaystyle 2n}$ de ${\displaystyle M}$ en procédant comme expliqué dans le paragraphe sur le théorème de Poincaré. La deuxième condition est que le nombre associé à toute surface sans bord est nul.

Le passage des espaces de phases aux variétés symplectiques générales est une grande généralisation mais on peut montrer qu'une variété symplectique ressemble toujours localement à un espace de phases. C'est le théorème de Darboux : au voisinage de n'importe quel point, toute variété symplectique peut être paramétré par un espace de phase de sorte que toute surface assez petite se voit attribuer le même nombre par la structure symplectique donnée et par la structure symplectique de l'espace des phases.

La question de savoir quels ensembles admettent au moins une structure symplectique est difficile. On connaît de nombreux exemples, des conditions nécessaires, d'autres qui sont suffisantes mais aucune caractérisation complète.

De même, une fois l'existence acquise on ne sait que très rarement combien de structures symplectiques réellement différentes cohabitent sur un même ensemble.

L'étude de la géométrie symplectique est née du constat que l'évolution d'un système mécanique préserve la structure symplectique canonique de l'espace des phases. Plus généralement on peut chercher à comprendre l'ensemble des transformations qui préservent une structure symplectique donnée. De telles transformations sont appelées symplectomorphismes et sont toujours très nombreuses, elles forment un ensemble de dimension infinie appelé groupe des symplectomorphismes. Pour comprendre la forme de cet ensemble, on cherche à le comparer à des ensembles plus petits que l'on comprend mieux. Les premiers résultats significatifs dans ce domaine sont dus à Gromov dans la foulée de son théorème de non tassement.

• Géométrie complexe : de nombreux exemples de structures symplectiques et de nombreuses questions viennent de la géométrie complexe. Ainsi pour (presque) toute équation polynomiale en plusieurs variables complexes, l'ensemble des solutions est muni d'une structure symplectique. L'étude de ces équations et des structures symplectiques s'éclairent l'une l'autre et c'est en transposant au cas symplectique général des idées nées dans le contexte de la géométrie complexe que Gromov a obtenu son théorème de non tassement et de nombreux autres résultats révolutionnaires.
• Géométrie de contact : la géométrie de contact est une autre branche de recherche en géométrie qui entretient des liens tellement étroits que certains auteurs présentent la géométrie de contact comme un analogue en dimension impaire de la géométrie symplectique. Sous des circonstances favorables, le bord éventuel d'une variété symplectique hérite d'une structure de contact (la variété symplectique est alors appelée remplissage de la variété de contact) ; de nombreux problèmes se posent, comme l'existence d'un tel remplissage ou l'existence de caractéristiques fermées (lire à ce sujet Conjecture de Weinstein).
• Systèmes dynamiques (différentiables) : les développements en géométrie symplectique ont été motivés par les conjectures d'Arnold concernant l'estimation du nombre minimal de points fixes d'un symplectomorphisme sur une variété symplectique compacte (voir #Histoire). En retour, l'intégration de champs de vecteurs spécifiques dépendant du temps sur des variétés symplectiques donnent lieu à une classe particulière de symplectomorphismes, appelés « difféomorphismes hamiltoniens ». Les appellations dynamique hamiltonienne et système hamiltonien sont d'usage courant.
• Ergodicité : la n-ième puissance d'une forme symplectique sur une variété de dimension 2n est une forme volume, préservée par les symplectomorphismes. Des travaux de Leonid Polterovich portent sur les propriétés ergodiques de ces difféomorphismes, et en particulier donnent des estimations de leurs entropies métriques.
• Géométrie riemannienne : une famille importante de variétés symplectiques est donnée par les variétés cotangentes.
• Géométrie algébrique : à la suite des travaux de Gromov, un certain nombre de concepts de géométrie complexe s'adaptent en géométrie symplectique : courbes holomorphes, invariants de Gromov-Witten, etc.

En 1687, Newton énonce la loi de l'attraction universelle. Cette loi permet de déduire le mouvement relatif d'une planète autour de son étoile, Kepler ayant décrit le mouvement elliptique des planètes dès 1611. Encore aujourd'hui, malgré l'avènement de la relativité générale, cette loi de la gravitation universelle est toujours utilisée dans la détection des exoplanètes. Une planète, à l'instar de la Terre, subit la force attractive du Soleil, et son évolution est décrite par l'équation différentielle :

${\displaystyle {\frac {\mathrm {d} ^{2}{\vec {r}}}{\mathrm {d} t^{2}}}=-\alpha {\frac {\vec {r}}{r^{3}}}.}$

Le problème du mouvement relatif de deux corps en interaction mutuelle est devenu un exercice classique incontournable du premier cycle universitaire. Newton lui-même en a donné une solution correcte dans les propositions 57 à 65 de ses Principia. La planète décrit par rapport à l'étoile un mouvement elliptique dont l'étoile est l'un des foyers. Six constantes sont nécessaires pour décrire ce mouvement :

• deux constantes t, u pour paramétrer le plan dans lequel le mouvement s'effectue ;
• deux constantes v, w pour décrire la position du second foyer dans ce plan ;
• une constante e, appelée l'excentricité, pour décrire l'ellipse ;
• et une constante θ pour décrire la position initiale de la planète.

Joseph-Louis Lagrange.

Toutefois, cette description oublie la présence d'autres planètes. Le problème à n corps (n ≥ 3) est autrement plus ardu. Il résiste encore aujourd'hui à trois siècles d'histoire. Aucune solution analytique n'est connue, excepté pour le problème à trois corps, pour lequel on sait déterminer certaines solutions dites « homographiques ».

De 1808 à 1811, Joseph-Louis Lagrange, alors professeur de mathématiques à l'École polytechnique, s'intéresse au problème de la stabilité des planètes du système solaire. Compte tenu du nombre de corps considérés, le problème est de taille ; il s'est depuis complexifié au fur et à mesure des avancées dans les observations astronomiques.

Grossièrement, la méthode de Lagrange consiste à effectuer des petites perturbations sur le mouvement d'une planète, autrement dit, sur les six constantes d'intégration. Cette perturbation varie dans le temps suivant une loi moyennant les forces subies :

${\displaystyle (t_{0},u_{0},v_{0},w_{0},e_{0},\theta _{0})\mapsto (t_{0}+t(t),u_{0}+u(t),v_{0}+v(t),w_{0}+w(t),e_{0}+e(t),\theta _{0}+\theta (t))}$

Les calculs n'étaient pas justifiés. Poincaré montre la divergence des séries utilisées par les astronomes dans Méthodes nouvelles de la mécanique céleste. Il faudra attendre la seconde moitié du XX^e siècle pour que les outils nécessaires soient introduits. La véritable révolution apportée par Lagrange est d'avoir introduit une fonctionnelle d'énergie, aujourd'hui notée L et appelée Lagrangien, dont les points critiques sont les trajectoires du mouvement.

L'intérêt croissant vis-a-vis des structures symplectiques durant les dernières décennies s'explique par les besoins de la physique du XX^e siècle. Le passage de la mécanique classique à la mécanique quantique est à ce jour encore mal compris. La question de fonder de sérieuses bases mathématiques est un défi qui a conduit les mathématiciens à s'interroger à nouveau sur la dynamique hamiltonienne (la mécanique classique, des systèmes dynamiques de points matériels à l'optique géométrique). Le regard porté à la lumière de la géométrie différentielle ne pouvait être que nouveau.

Dans la continuation des travaux de Lagrange et de Hamilton, pour établir l'existence d'orbites périodiques dans le problème des trois corps, Henri Poincaré se ramène à l'étude d'une application préservant l'aire sur un anneau ${\displaystyle S^{1}\times [-1,1]}$. Cette application s'est avérée par la suite d'une grande utilité dans l'étude des flots de champs de vecteurs. Elle est aujourd'hui connue sous le nom d'application de retour de Poincaré.

Les résultats énoncés par Poincaré furent démontrés dans les années 1920 par George David Birkhoff^{[réf. souhaitée]} ; ils sont aujourd'hui considérés comme les premiers travaux sur la géométrie symplectique - s'ils peuvent être considérés comme tels. Le théorème de Poincaré-Birkhoff affirme l'existence de points fixes pour un difféomorphisme de l'anneau ${\displaystyle S^{1}\times [-1,1]}$, qui préserve la mesure de Lebesgue, et qui fait tourner ${\displaystyle S^{1}\times {1}}$ dans le sens positif et ${\displaystyle S^{1}\times {-1}}$ dans le sens négatif. En réalité, ces résultats portaient davantage sur la préservation du volume. Mais en dimension 2, une mesure est essentiellement une forme d'aire, donc une forme symplectique. La dimension 2 reflète mal les particularités propres à la géométrie symplectique.

Le théorème de Poincaré-Birkhoff préfigure la conjecture d'Arnold, énoncée au début des années 1960. Cette conjecture s'efforce de trouver un minorant du nombre d'orbites périodiques pour un difféomorphisme symplectique sur une variété symplectique compacte. En 1983 Conley (de) et Zehnder démontrent la conjecture pour le tore par une étude variationnelle. Inspiré de ces travaux, Andreas Floer démontre en partie la conjecture pour une large classe de variétés symplectiques compactes, étendue par la suite par Alan Weinstein. Les méthodes utilisées ont contribué à la mise en place de l'homologie de Floer. La formulation de cette homologie représente un des aspects les plus puissants mis en place ces dernières décennies.

Brièvement, et du moins sous certaines hypothèses, l'homologie de Floer consiste à compter des orbites périodiques d'une isotopie hamiltonienne et, modulo translation, des cylindres reliant ces orbites répondant à une EDP elliptique. L'ellipticité joue un rôle central.

Le théorème KAM figure parmi les résultats les plus cités en dynamique hamiltonienne. Il étudie la stabilité des systèmes mécaniques complètement intégrables. Le nom du théorème est l'abréviation des trois mathématiciens qui ont contribué à sa démonstration : Kolmogorov, Arnold et Moser. Il justifie dans le langage actuel des mathématiques les résultats de Lagrange.

Une autre investigation importante concerne l'introduction des capacités symplectiques. Ce sont des invariants symplectiques vérifiant de bonnes conditions de normalisation et d'homogénéité. Leur classification reste totalement incomprise à ce jour. Il existe un grand nombre de capacités introduites[4] : le rayon de Gromov, lié au théorème de non-plongement de Gromov ; les capacités d'Ekeland-Hofer et de Hofer-Zehnder, utilisant des études variationnelles sur la dynamique hamiltonienne ; ou encore un grand nombre de capacités dites spectrales dont l'introduction a été initiée par Claude Viterbo. L'utilisation de ces capacités a permis une preuve partielle de la conjecture de Weinstein (évoquée plus haut), et une preuve du théorème de rigidité de Gromov.

L'usage d'une généralisation des courbes holomorphes a porté de forts développements en géométrie symplectique.

La géométrie symplectique s'est constituée comme domaine d'étude à part entière dès la fin des années 1960. Ce nouveau souffle dans la recherche mathématique a introduit parallèlement d'autres disciplines, la quantification géométrique et la théorie symplectique des champs (en). Récemment, des avancées significatives ont été réalisées par Jean-Claude Sikorav et Claude Viterbo : il a été montré que si ${\displaystyle X}$ est une variété fermée, alors toute sous-variété lagrangienne de ${\displaystyle T\star X}$ isotope à la section nulle ${\displaystyle \{(x;0)|x\in X\}}$ admet une fonction génératrice quadratique à l'infini, et que de plus, toutes les fonctions génératrices quadratiques à l'infini d’une telle sous-variété sont équivalentes. Ce théorème a par la suite été étendu par Yu Chenakov, qui a montré que l'existence de cette classe de fonctions génératrices s'étendait aux variétés non compactes, pour les sous-variétés legendriennes.

• (en) Anatoli Fomenko, Symplectic Geometry (2^e édition) (1995) Gordon and Breach Publishers, (ISBN 978-2-88124-901-3)
• (en) Alan D. Weinstein, Lectures on Symplectic Manifolds [détail des éditions]
• (en) Vladimir Arnold, Mathematical methods of classical mechanics [détail des éditions]
• (en) Jaume Amorós, Fedor Bogomolov, Ludmil Katzarkov, Tony Pantev, « Symplectic Lefschetz fibrations with arbitrary fundamental groups », J. Differential Geom., vol. 54, n° 3, 2000, p. 489-545.
• Charles-Michel Marle, Géométrie symplectique et géométrie de Poisson (2018), Calvage & Mounet (ISBN 978-2-916352-70-1)

• Lexique de la géométrie symplectique

• (en) Yakov Eliashberg, « Symplectic topology in the nineties », Differential Geometry and its Applications, Volume 9, Issues 1-2, August 1998, Pages 59–88.

  Article listant les principaux articles de géométrie symplectique publiés avant 1998.

• Patrick Iglesias-Zemmour, Les origines du calcul symplectique chez Lagrange

  Article sur la méthode des variations des constantes de Lagrange, amplement argumentés, abordable par le grand public.

• Patrick Iglesias-Zemmour, Aperçu des origines de la géométrie symplectique

  Article sur l'histoire de la géométrie symplectique avec la correction d'idées faussement communément admises.

• Michèle Audin et Patrick Iglesias, De la mécanique à la géométrie symplectique

  Exposé sur le mérite de Lagrange et rapide résumé de l'histoire des mathématiques qui a conduit à la formulation de la géométrie symplectique.

• Portail de la géométrie