Tout d'abord, il est clair que les fonctions proposées définissent bien des normes (propriétés classiques de la valeur absolue et du module).

Soit ${\displaystyle \|\cdot \|}$ une norme sur ${\displaystyle \mathbb {K} }$.

Par définition, ${\displaystyle \forall x\in \mathbb {K} \quad \|x\|=\|x.1\|=|x|.\|1\|}$.

On a donc le résultat en posant ${\displaystyle a=\|1\|>0}$.

1. 

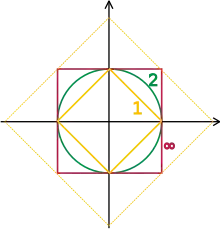   Les cercles unité (en gras) associés aux trois normes.
2. La figure montre que ${\displaystyle \|(x,y)\|_{1}\geq \|(x,y)\|_{2}\geq \|(x,y)\|_{\infty }}$, avec égalités si ${\displaystyle \{|x|,|y|\}=\{0,1\}}$, et que ${\displaystyle \|(x,y)\|_{\infty }\geq {\frac {1}{2}}\|(x,y)\|_{1}}$, avec égalité si ${\displaystyle |x|=|y|=1}$.
   Il est très facile (cf. question suivante) de redémontrer algébriquement ces trois inégalités (et les cas d'égalité).
   Pour la comparaison entre ${\displaystyle \|\cdot \|_{1}}$ et ${\displaystyle \|\cdot \|_{\infty }}$, on a même trouvé les constantes optimales : ${\displaystyle \|(x,y)\|_{\infty }\leq \|(x,y)\|_{1}\leq 2\|(x,y)\|_{\infty }}$. On les trouve de même pour les deux autres paires (en dilatant l'une des deux boules jusqu'à contenir l'autre) : ${\displaystyle \|(x,y)\|_{\infty }\leq \|(x,y)\|_{2}\leq {\sqrt {2}}\|(x,y)\|_{\infty }}$ et ${\displaystyle \|(x,y)\|_{2}\leq \|(x,y)\|_{1}\leq {\sqrt {2}}\|(x,y)\|_{2}}$.
3. Soit ${\displaystyle x=(x_{1},\ldots ,x_{n})\in \mathbb {K} ^{n}}$.
   • Montrons tout d'abord que les normes ${\displaystyle \|\cdot \|_{\infty }}$ et ${\displaystyle \|\cdot \|_{1}}$ sont équivalentes.
     On a : ${\displaystyle \|x\|_{1}=\sum _{i=1}^{n}|x_{i}|\leq \sum _{i=1}^{n}\|x\|_{\infty }=n\|x\|_{\infty }}$
     et comme il existe ${\displaystyle i\in \{1,\ldots ,n\}}$ tel que ${\displaystyle \|x\|_{\infty }=|x_{i}|}$, on a ${\displaystyle \|x\|_{\infty }\leq \|x\|_{1}}$.
     Ces inégalités sont optimales. On le vérifie en prenant ${\displaystyle x=(1,1,\ldots ,1)}$ pour la première et ${\displaystyle x=(1,0,\ldots ,0)}$ pour la deuxième.
   • Montrons maintenant que les normes ${\displaystyle \|\cdot \|_{\infty }}$ et ${\displaystyle \|\cdot \|_{2}}$ sont équivalentes. Soit ${\displaystyle y=(x_{1}^{2},\ldots ,y_{n}^{2})}$. Alors, ${\displaystyle \|x\|_{2}^{2}=\|y\|_{1}}$ et ${\displaystyle \|x\|_{\infty }^{2}=\|y\|_{\infty }}$ donc d'après ce qui précède, ${\displaystyle \|x\|_{\infty }\leq \|x\|_{2}\leq {\sqrt {n}}\|x\|_{\infty }}$ et ces inégalités sont optimales à l'aide des mêmes exemples.
   • Il en résulte que ${\displaystyle \|\cdot \|_{1}}$ et ${\displaystyle \|\cdot \|_{2}}$ sont équivalentes mais il reste à déterminer pour elles les constantes optimales.
     On a, par l'inégalité de Cauchy-Schwarz : ${\displaystyle \sum _{i=1}^{n}|x_{i}|\leq {\sqrt {\sum _{i=1}^{n}1}}{\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}}$, soit ${\displaystyle \|x\|_{1}\leq {\sqrt {n}}\|x\|_{2}}$.
     On a : ${\displaystyle \|x\|_{2}=\sum _{i=1}^{n}|x_{i}|^{2}\leq \left(\sum _{i=1}^{n}|x_{i}|\right)^{2}=\|x\|_{1}^{2}}$ donc ${\displaystyle \|x\|_{2}\leq \|x\|_{1}}$.
     Les mêmes exemples montrent que les inégalités sont optimales.

   Plus généralement, ${\displaystyle 1\leq r\leq p\leq \infty \Rightarrow \|\cdot \|_{p}\leq \|\cdot \|_{r}\leq n^{{\frac {1}{r}}-{\frac {1}{p}}}\|\cdot \|_{p}}$, la seconde inégalité se déduisant de l'inégalité de Hölder.

1. • ${\displaystyle \|\cdot \|_{1}}$ est même une norme sur l'espace des fonctions intégrables de ${\displaystyle \left[0,1\right]}$ dans ${\displaystyle \mathbb {R} }$, dont ${\displaystyle \mathbb {R} [X]}$ s'identifie à un sous-espace.
   • ${\displaystyle P\mapsto |P(0)|+\|P'\|_{1}}$ est une semi-norme (c'est-à-dire qu'elle est positivement homogène et sous-additive) car les deux applications dont elle est la somme sont semi-normes. En effet, plus généralement, la composée d'une semi-norme et d'une application linéaire est une semi-norme. De plus, si ${\displaystyle |P(0)|+\|P'\|_{1}=0}$ alors ${\displaystyle P(0)=0}$ et ${\displaystyle P'=0}$ donc ${\displaystyle P=P(0)=0}$.
   • ${\displaystyle \|\cdot \|_{\infty }}$ est même une norme sur l'espace des fonctions bornées de ${\displaystyle \left[0,1\right]}$ dans ${\displaystyle \mathbb {R} }$. En effet, c'est une semi-norme (comme sup d'une famille d'applications qui, par le principe général énoncé au point précédent, sont des semi-normes) et elle ne s'annule qu'en 0.
2. C'est une semi-norme (toujours par le même principe général) et elle ne s'annule qu'en 0, car si ${\displaystyle P\in \mathbb {R} _{n}[X]}$ a ${\displaystyle n+1}$ racines distinctes alors ${\displaystyle P=0}$.
3. Sur ${\displaystyle \mathbb {R} _{n}[X]}$, toutes les normes sont équivalentes.
4. Non car ${\displaystyle \|X^{n}\|_{\infty }=1}$ tandis que ${\displaystyle \|X^{n}\|_{1}={\frac {1}{n+1}}}$.

Les questions 1 et 2 sont des rappels de cours sur les espaces euclidiens qu'il est important de savoir démontrer.

1. Voir Espace préhilbertien réel/Formes bilinéaires symétriques.
2. Voir Espace préhilbertien réel/Produit scalaire.
3. Calculons simplement en utilisant les propriétés du produit scalaire. Soit ${\displaystyle x,\ y\in E}$ :

   ${\displaystyle \|x-y\|^{2}+\|x+y\|^{2}=\langle x-y\mid x-y\rangle +\langle x+y\mid x+y\rangle =\langle x\mid x\rangle -2\langle x\mid y\rangle +\langle y\mid y\rangle +\langle x\mid x\rangle +2\langle x\mid y\rangle +\langle y|y\rangle =2(\|x\|^{2}+\|y\|^{2})}$

4. Considérons les vecteurs ${\displaystyle x=(1,0,\cdots ,0)}$ et ${\displaystyle y=(0,1,0,\cdots ,0)}$. On a alors :

   ${\displaystyle \|x-y\|_{\infty }^{2}+\|x+y\|_{\infty }^{2}=2}$ et ${\displaystyle 2(\|x\|_{\infty }^{2}+\|y\|_{\infty }^{2})=4}$.

   La norme infinie ne peut donc provenir d'un produit scalaire.

5. 1. D'après l'identité du parallélogramme, ${\displaystyle N(x+y+z)^{2}=2\left(N(x)^{2}+N(y+z)^{2}\right)-N(y+z-x)^{2}}$.
      Cette égalité, jointe à son homologue lorsqu'on remplace ${\displaystyle z}$ par ${\displaystyle -z}$, donne :

      ${\displaystyle B(x+y,z)={\frac {1}{2}}\left[N(y+z)^{2}-N(y-z)^{2}\right]-{\frac {1}{4}}\left[N(y+z-x)^{2}-N(y-z-x)^{2}\right]=2B(y,z)-B(y-x,z)}$.

   2. On en déduit (en intervertissant ${\displaystyle x}$ et ${\displaystyle y}$) : ${\displaystyle B(x+y,z)=2B(x,z)-B(x-y,z)=2B(x,z)+B(y-x,z)}$
      puis (en prenant la moyenne) : ${\displaystyle B(x+y,z)=B(x,z)+B(y,z)}$.
   3. Une récurrence immédiate utilisant la question précédente montre que ${\displaystyle \forall n\in \mathbb {N} \quad B(nx,y)=nB(x,y)}$, ce qui — puisque ${\displaystyle B(-x,y)=-B(x,y)}$ — permet d'affirmer que ${\displaystyle \forall n\in \mathbb {Z} \quad B(nx,y)=nB(x,y)}$.
      Finalement, soit ${\displaystyle r={\frac {p}{q}}\in \mathbb {Q} }$ avec ${\displaystyle p,\ q}$ deux nombres entiers. On a alors ${\displaystyle B(rx,y)=rB(x,y)}$ car

      ${\displaystyle qB(rx,y)=B(qrx,y)=B(px,y)=pB(x,y)=qrB(x,y)}$.

   4. L'application ${\displaystyle t\mapsto B(tx,y)}$ est continue sur ${\displaystyle \mathbb {R} }$ (par définition de ${\displaystyle B}$ et continuité de ${\displaystyle N}$) et coïncide sur ${\displaystyle \mathbb {Q} }$ avec ${\displaystyle t\mapsto tB(x,y)}$. Par densité de ${\displaystyle \mathbb {Q} }$ dans ${\displaystyle \mathbb {R} }$, ces deux applications sont donc égales, ce qui termine de montrer que ${\displaystyle B}$ est linéaire à gauche.

1. Il s'agit essentiellement de vérifications élémentaires, le seul point délicat étant l'inégalité triangulaire pour la norme 2. Nous allons donc uniquement traiter ce cas.

   Soit ${\displaystyle f\in C([a,b],\mathbb {R} )}$ et ${\displaystyle \lambda \in \mathbb {R} }$.

   Alors ${\displaystyle \|\lambda f\|_{2}={\sqrt {\int _{a}^{b}|\lambda f(t)|^{2}\,\mathrm {d} t}}=|\lambda |{\sqrt {\int _{a}^{b}|f(t)|^{2}\,\mathrm {d} t}}=|\lambda |\|f\|_{2}}$.

   On a : ${\displaystyle \|f\|_{2}=0\Leftrightarrow \int _{a}^{b}|f(t)|^{2}\,\mathrm {d} t=0\Leftrightarrow f^{2}=0\Leftrightarrow f=0}$. Ici, la continuité de ${\displaystyle f}$ est essentielle pour conclure.

   Pour l'inégalité triangulaire, la clef est dans l'inégalité de Cauchy-Schwarz pour les intégrales, ce qui donne :

   ${\displaystyle {\begin{aligned}\int _{a}^{b}|f(t)+g(t)|^{2}\,\mathrm {d} t&\leq \|f\|_{2}^{2}+\|g\|_{2}^{2}+2\int _{a}^{b}|f(t)g(t)|\,\mathrm {d} t\\&\leq \|f\|_{2}^{2}+\|g\|_{2}^{2}+2\|f\|_{2}\|g\|_{2}\\&\leq \left(\|f\|_{2}+\|g\|_{2}\right)^{2},\end{aligned}}}$

   ce qui prouve l'inégalité triangulaire en prenant la racine carrée.

2. • La première des inégalités se déduit de l'inégalité de Cauchy-Schwarz :

   ${\displaystyle \int _{a}^{b}|f(t)|\,\mathrm {d} t=\int _{a}^{b}|f(t)\times 1|\,\mathrm {d} t\leq {\sqrt {\int _{a}^{b}1\,\mathrm {d} t}}\|f\|_{2}={\sqrt {b-a}}\|f\|_{2}}$

   • La seconde se montre en constatant que ${\displaystyle \forall t\in [a,b]\quad |f(t)|\leq \|f\|_{\infty }}$ par définition de la borne supérieure. On a alors :

   ${\displaystyle {\sqrt {\int _{a}^{b}|f(t)|^{2}\,\mathrm {d} t}}\leq \|f\|_{\infty }{\sqrt {\int _{a}^{b}\,\mathrm {d} t}}={\sqrt {b-a}}\|f\|_{\infty }}$

   On montre qu'elles sont optimales en prenant la fonction constante égale à 1 sur ${\displaystyle [a,b]}$.

3. Comme mentionné dans le cours, pour montrer que les normes ne sont pas deux à deux équivalentes, on va construire une suite de fonctions ${\displaystyle (f_{n})}$ tels que ${\displaystyle {\frac {\|f_{n}\|_{\infty }}{\|f_{n}\|_{1}}}\to +\infty }$ pour commencer.

   On pose, pour tout ${\displaystyle n\in \mathbb {N} }$ : ${\displaystyle f_{n}:t\mapsto \left({\frac {t-a}{b-a}}\right)^{n}}$.

   On trouve alors : ${\displaystyle \|f_{n}\|_{\infty }=1,\ \|f_{n}\|_{1}={\frac {b-a}{n+1}},\ {\text{et}}\ \|f_{n}\|_{2}={\sqrt {\frac {b-a}{2n+1}}}}$.

   Ceci montre bien que les trois rapports : ${\displaystyle {\frac {\|f_{n}\|_{\infty }}{\|f_{n}\|_{1}}},\ {\frac {\|f_{n}\|_{\infty }}{\|f_{n}\|_{2}}},\ {\frac {\|f_{n}\|_{2}}{\|f_{n}\|_{1}}}}$ tendent vers ${\displaystyle +\infty }$, et donc que les trois normes ne sont pas équivalentes.

C'est immédiat pour ${\displaystyle \lambda N_{1}}$. Montrons-le pour ${\displaystyle N_{1}+N_{2}}$.

Nous avons déjà remarqué (Exercice 1-3) que la somme de deux semi-normes est une semi-norme.

Enfin, si ${\displaystyle (N_{1}+N_{2})(x)=0}$ alors ${\displaystyle N_{1}(x)=0}$ (par exemple) donc ${\displaystyle x=0}$.

1. Les applications ${\displaystyle N_{t}:(x,y)\mapsto {\frac {|x+ty|}{1+t^{2}}}}$ (pour ${\displaystyle t\in \mathbb {R} }$) sont clairement des semi-normes et leur sup ${\displaystyle N}$ est fini (cf. question suivante), donc ${\displaystyle N}$ est une semi-norme.
   C'est une norme car de plus, si ${\displaystyle N(x,y)=0}$ alors ${\displaystyle \forall t\in \mathbb {R} \quad N_{t}(x,y)=0}$, en particulier ${\displaystyle N_{0}(x,y)=0}$ et ${\displaystyle N_{1}(x,y)=0}$, donc ${\displaystyle |x|=0}$ et ${\displaystyle |x+y|=0}$, donc ${\displaystyle (x,y)=(0,0)}$.
2. D'après l'inégalité de Cauchy-Schwarz dans ${\displaystyle \mathbb {R} ^{2}}$ muni de son produit scalaire canonique, ${\displaystyle |x+ty|\leq \|(x,y)\|_{2}\|(1,t)\|_{2}}$ donc ${\displaystyle N(x,y)\leq {\underset {t\in \mathbb {R} }{\sup }}{\frac {\|(x,y)\|_{2}\|(1,t)\|_{2}}{1+t^{2}}}={\underset {t\in \mathbb {R} }{\sup }}{\frac {\|(x,y)\|_{2}}{\sqrt {1+t^{2}}}}=\|(x,y)\|_{2}}$.
3. ${\displaystyle N(x,y)\leq 1\Leftrightarrow \forall t\in \mathbb {R} \quad |x+ty|\leq 1+t^{2}\Leftrightarrow \forall t\in \mathbb {R} \quad x+ty\leq 1+t^{2}{\text{ et }}-x-ty\leq 1+t^{2}}$${\displaystyle \Leftrightarrow \forall t\in \mathbb {R} _{+}\quad |x|\leq 1+t^{2}-t|y|\Leftrightarrow |x|\leq 1+(|y|/2)^{2}-(|y|/2)|y|\Leftrightarrow |x|\leq 1-y^{2}/4}$
   donc la boule unité pour la norme ${\displaystyle N}$ est la partie bornée délimitée par les deux arcs de parabole ${\displaystyle x=\pm (1-y^{2}/4),\;y\in [-2,2]}$. Graphique Google.