Tenseur (mathématiques)
Les tenseurs sont des objets mathématiques issus de l'algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs. On les rencontre notamment en analyse vectorielle et en géométrie différentielle fréquemment utilisés au sein de champs de tenseurs. Ils sont aussi utilisés en mécanique des milieux continus.
Le présent article ne se consacre qu'aux tenseurs dans des espaces vectoriels de dimension finie, bien que des généralisations en dimension infinie et même pour des modules existent.
Principe général
Le principe est de généraliser les notions de scalaires et de vecteurs en dimension finie. Les tenseurs d'un type donné sont eux-mêmes membres d'un espace vectoriel :
- ils possèdent une addition et un produit par les scalaires ;
- ils sont indépendants d'un choix de base mais peuvent être représentés par des tableaux à plusieurs entrées pour un choix de base donnée.
S'y ajoutent deux opérations : un produit, dit tensoriel, permettant de multiplier deux tenseurs (éventuellement de natures distinctes) ainsi qu'une application linéaire qui réduit leur taille, appelée contraction.
Comme évoqué ci-dessus les scalaires et les vecteurs constituent des exemples simples de tenseurs. Dans une base donnée, un vecteur (tenseur d'ordre 1) peut être représenté par la donnée d'un n-uplet de coordonnées. Les matrices n×n — qui peuvent représenter suivant les cas des endomorphismes, des bivecteurs ou encore des formes bilinéaires — forment une extension des n-uplets similaire à l'extension que représente les n-uplets par rapport aux scalaires. Les objets descriptibles par des matrices constituent donc les premiers types de tenseurs non triviaux, appelés tenseurs d'ordre 2. En prolongeant la réflexion on peut imaginer, toujours de manière informelle, des matrices cubiques n×n×n, correspondant aux tenseurs d'ordre 3, et ainsi de suite.
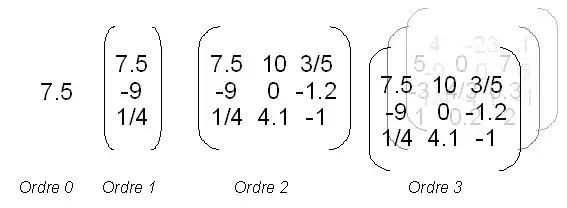
Les deux opérations classiques de la manipulation des tenseurs peuvent être intuitivement illustrées par certaines opérations matricielles. Il est en effet connu qu'en multipliant une matrice colonne par une matrice ligne (c'est-à-dire deux n-uplets) on obtient une matrice carrée (ou rectangulaire si les opérandes n'ont pas la même dimension). Il existe donc des transformations permettant d'augmenter l'ordre des tenseurs. Cette idée est à la base du produit tensoriel.
Inversement, le produit d'une matrice ligne par une matrice colonne se réduit à un scalaire. On voit ici apparaître l'idée de contraction.
Produit tensoriel d'espaces vectoriels de dimensions finies
Il est pratique, avant d'étudier le produit tensoriel de vecteurs et de donner un sens plus précis au terme tenseur, de considérer les espaces vectoriels qui interviennent dans sa définition. On note que le même symbole, à savoir , est utilisé pour construire à la fois les tenseurs et les espaces auxquels ils appartiennent.
On notera par la suite l'espace vectoriel des applications k-linéaires de dans (c'est-à-dire linéaires par rapport à chacune de leurs k variables).
Définitions
Soient et deux espaces vectoriels de dimension finie sur un corps commutatif (en pratique il s'agit souvent de ou de mais d'autres corps sont possibles). On note le dual de . Le produit tensoriel de par — noté , ou s'il n'y a pas d'ambiguïté sur le corps — est un cas particulier de produit tensoriel de modules. Une définition plus simple[1] peut être ici de le définir comme l'espace vectoriel des formes bilinéaires sur le couple d'espaces vectoriels .
On rappelle par ailleurs qu'en dimension finie, on assimile sans problème à son bidual . On a donc de même :
Dans la théorie des catégories, les -espaces vectoriels (de dimension finie mais on peut généraliser en dimension quelconque) forment un exemple standard de catégorie monoïdale pour le produit tensoriel ainsi défini.
Associativité
Les espaces vectoriels , et sont canoniquement isomorphes. Cette propriété permet de considérer le produit tensoriel comme associatif et d'assimiler le produit de k espaces de dimensions finies à l'espace des formes k-linéaires sur les espaces duaux. La mise en parenthèse est donc inutile :
Dimension
La dimension d'un produit tensoriel d'espaces est égale au produit des dimensions de tous les espaces.
Le corps des scalaires
étant un espace vectoriel de dimension 1 sur lui-même, il peut être utilisé dans le produit tensoriel. et sont canoniquement isomorphes à . On peut donc considérer comme une sorte d'élément neutre.
Puissances tensorielles
On peut définir la -ième puissance tensorielle d'un espace , notée ou , par :
- pour , ;
- pour , en extrapolant les définitions précédentes, ;
- pour , le choix de permet de généraliser les formules de manière cohérente.
On a par ailleurs les propriétés :
Dualité
Encore une fois par isomorphisme canonique on a :
Espaces des applications linéaires et multilinéaires
L'espace vectoriel des applications linéaires de dans est canoniquement isomorphe à . Plus généralement, l'espace des applications k-linéaires de dans est canoniquement isomorphe à . Il est donc possible de confondre ces espaces.
À propos de la commutativité
Il existe un isomorphisme entre et . En pratique les assimiler (c'est-à-dire rendre commutatif) n'est cependant pas toujours une bonne chose. C'est en particulier problématique lorsque . En effet, cette assimilation pourrait dans ce cas amener à croire que le produit tensoriel de deux éléments (décrit ci-dessous) est commutatif, ce qui n'est pas le cas.
Dans la suite de cet article on considérera donc, sauf mention contraire, et comme deux espaces distincts. Les considérations liées à leur isomorphismes sont abordées dans ce paragraphe.
Tenseurs et produit tensoriel sur les éléments
L'intérêt premier du produit tensoriel est de définir une opération sur les vecteurs (ou plus généralement les éléments des modules) ayant des propriétés similaires à celle d'un produit. Cela dit, contrairement aux produits habituels, le produit tensoriel n'est pas une opération interne : il peut s'effectuer sur des vecteurs issus d'espaces vectoriels différents et son résultat (à quelques exceptions près) n'appartient à aucun des espaces en question. Les éléments intervenant dans de tels produits portent le nom de tenseurs.
Définition
Soit et deux formes linéaires. On notera l'application définie par :
Il s'agit d'une forme bilinéaire : on a donc . Le produit se généralise facilement aux formes multilinéaires.
Comme en dimension finie , tout vecteur (respectivement ) peut être assimilé à une forme linéaire sur (respectivement ). On définit ainsi de manière générale le produit tensoriel de et , noté , comme forme bilinéaire sur .

La forme bilinéaire est donc un tenseur appartenant à . La forme bilinéaire est quant à elle un tenseur appartenant à . Les tenseurs peuvent donc être définis (en dimension finie) comme des formes multilinéaires munis d'un produit .
Remarques
- Réciproquement, tout tenseur ne s'écrit pas nécessairement comme un produit . En revanche, il peut toujours être décomposé en combinaison linéaire d'éléments de la forme où et . C'est-à-dire qu'on peut toujours trouver des familles de vecteurs et et une famille de scalaires telles que .
- On note bien que tout vecteur est un type de tenseur particulier (il est toujours assimilable à une forme 1-linéaire) et que tout tenseur fait partie d'un espace vectoriel. L'utilisation du terme tenseur sous-entend l'usage du produit tensoriel. En pratique le terme tenseur est surtout utilisé à propos de produits de vecteurs d'un même espace ou de son dual .
Associativité
Grâce à l'isomorphisme canonique on peut considérer que le produit tensoriel est associatif. Autrement dit . De plus on peut voir le tenseur comme une forme trilinéaire : . D'une manière générale si on se donne vecteurs , le tenseur est un élément de . C'est donc une forme -linéaire.

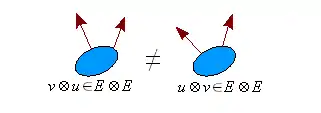
Non commutativité
Si et , les tenseurs et appartiennent alors tous les deux au même espace . Néanmoins on prendra bien soin de noter que dans le cas général .
Distributivité
Le produit tensoriel se comporte bien comme un produit vis-à-vis de l'addition des espaces vectoriels :
Généralisation des produits usuels
On notera que le produit tensoriel généralise le produit par un scalaire défini sur les -espaces vectoriels ainsi que le produit dans le corps . On a ainsi et .

Bases des espaces produits
Soit une base de et une base de . Alors la famille forme une base de . Par conséquent tout élément admet une unique famille de coordonnées sur cette base :
Cette formule est bien cohérente avec le fait que . Les coordonnées sont explicitement calculables en utilisant les bases duales et par la formule :
Ces formules se généralisent pour espaces vectoriels.
Opération de contraction
Définition
Soit un espace vectoriel de dimension finie sur un corps tel que . On suppose qu'il existe deux indices et tels que (ou de manière complètement équivalente ). Soit une base de ; la base duale est donc une base de . Étant donné un tenseur , l'application
est une forme -linéaire sur , autrement dit un tenseur de . Par ailleurs cette forme est indépendante du choix de la base de . L'opération s'appelle contraction de sur les indices et . Elle est parfois notée

Il est important de garder à l'esprit que l'opération de contraction n'est possible que pour deux indices correspondant à des espaces duaux entre eux et n'a aucun sens dans d'autres cas. Il s'agit en outre d'une opération linéaire de dans .
Produit contracté
En pratique la contraction est souvent utilisée au sein d'une opération appelée produit contracté et notée , ou même simplement . Le produit contracté de deux tenseurs est le résultat de leur produit tensoriel suivi d'une contraction d'un indice du premier par un indice du second. On notera que les notations sont lacunaires : elles ne précisent pas quels sont les indices de contraction. Par défaut, il s'agit en général du dernier indice du premier tenseur et du premier indice du second. Comme pour la contraction, le produit contracté n'a de sens que si les indices contractés correspondent à des espaces duaux.

Associativité
Le produit contracté est associatif si le tenseur du centre a au moins deux indices. Ainsi pour , et , on a bien . Si le tenseur du centre n'a qu'un indice, il est possible que l'un des deux parenthésages n'ait pas de sens, et même dans le cas contraire, l'égalité ne sera pas réalisée dans le cas général.
Distributivité
Le produit contracté se comporte bien comme un produit vis-à-vis de l'addition des espaces vectoriels :
Image par le tenseur ou produit contracté
Étant donné un tenseur et vecteurs tels que on peut effectuer deux opérations :
- calculer l'image des vecteurs par (qui, rappelons-le, peut toujours être vue comme une forme multilinéaire) : ;
- calculer les produits contractés successifs de par chaque vecteur .
Il s'agit en fait d'une seule et même opération :

D'une manière plus générale, si le tenseur construit en évaluant la -ème position de est égal au produit contracté de en son -ème indice par en son unique indice. Dès lors il devient possible d'occulter complètement l'aspect fonctionnel de pour ne considérer que ses propriétés algébriques.
Crochet de dualité
Le crochet de dualité est donc un cas particulier du produit contracté : .
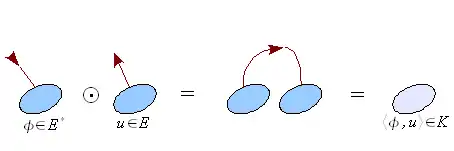
Image par une application linéaire
L'application linéaire pouvant être vue comme un tenseur , on peut calculer l'image d'un vecteur comme étant le produit contracté .
Composée d'applications linéaires
Si et sont représentées par les tenseurs et , alors l'application composée peut être représentée par le tenseur .
Produit contracté plusieurs fois
La contraction peut être exercée plusieurs fois à la suite d'un produit tensoriel. Par exemple le produit doublement contracté (noté , ou par deux points dans un cercle) correspond à deux contractions successives après un produit tensoriel. Là encore les indices de contractions n'étant en général pas précisés, le produit doublement contracté correspond souvent à la contraction du dernier indice de par le premier de et de l'avant dernier de par le deuxième de .

On peut définir de même un produit fois contracté si les tenseurs le permettent.
Permutation d'indices
Les espaces et peuvent être mis en relation via un isomorphisme qui consiste simplement à inverser l'ordre des indices. Ainsi à tout on peut associer un unique élément de , que l'on notera , tel que :
Ce principe se généralise pour espaces. Soit un espace vectoriel de dimension finie sur un corps et une permutation. On peut définir un isomorphisme qui a tout élément de associe un tenseur de , défini par :
On voit bien qu'une permutation induit naturellement un isomorphisme entre les espaces et .
Pour des raisons de commodité, on peut utiliser la notation canonique des permutations consistant à n'indiquer que la liste différentes permutations circulaires. Ainsi l'application transforme l'indice 1 en l'indice 2, l'indice 2 en l'indice 5, l'indice 5 en l'indice 1 et laisse invariant les autres indices.

En théorie des catégories, ce type d'applications, qui fournit une notion proche de la commutativité, est étudié dans le cadre des catégories monoïdales tressées.
Non unicité de l'isomorphisme
Pour des espaces et donnés à priori, l'existence d'une telle application n'implique cependant pas nécessairement son unicité. Supposons en effet qu'un espace est présent plusieurs fois dans le produit . Si l'espace est un produit des mêmes (mais dans un ordre éventuellement différent), il existe plus d'une permutation telle que soit un isomorphisme de dans . Ainsi pour et , on peut utiliser comme isomorphisme les applications , , , , et .
peut être mis en relation avec lui-même via deux permutations : l'identité et l'application . En généralisant à un ordre quelconque, l'espace peut être muni d'un groupe d'automorphismes constitué de telles applications. Ce groupe est en outre isomorphe à .
C'est cette absence d'unicité dans le cas général qui oblige à tenir compte de l'ordre des indices. De fait, on s'abstient en règle générale de considérer le produit tensoriel d'espaces comme commutatif.
Transposition
Dans le cas de produit de deux espaces, l'application peut être appelée transposition. Cette notion est cohérente avec celle de transposition d'application linéaire. On sait en effet qu'une application linéaire de dans peut être représentée par un tenseur . Le tenseur transposé , élément de représente alors l'application transposée , application de dans .

Composition et inverse
Pour deux permutations et de , on a :
Algèbre des tenseurs
Définition
Étant donné un espace vectoriel de dimension finie on appelle tenseur sur fois contravariant et fois covariant (ou tenseur ) tout élément de . et sont les variances de ce type de tenseur, est leur ordre (ou rang). Les tenseurs de type forment un espace vectoriel. On fixe les notations :
L'algèbre des tenseurs de notée est définie suivant les auteurs, soit comme la somme directe des espaces des tenseurs contravariants, soit comme la somme directe des espaces des tenseurs à la fois contravariants et covariants. Afin de distinguer ces deux cas, on adopte les notations suivantes (non conventionnelles) :
Les algèbres et sont des algèbres sur le corps . Ce sont même des algèbres graduées sur respectivement et ; toutes deux de dimension infinie.
L'algèbre extérieure sur notée possède des liens privilégiés avec l'algèbre du fait d'une possible injection des espaces dans .
Éléments
- L'algèbre tensorielle est surtout définie afin de donner une structure générale à l'ensemble des tenseurs. Ceci nécessite de prolonger l'addition qui n'est a priori pas définie entre les éléments de et de si . Il faut pour cela introduire des éléments supplémentaires. Ainsi en considérant par exemple le cas de , un élément est formellement une suite telle que et, par définition des sommes directes, dont seul un nombre fini d'éléments est non nul. Néanmoins en physique et dans beaucoup d'applications seuls les éléments appartenant à des sous-espaces de type ou sont pris en considération (ce sont les seuls pour lesquels les notions d'ordre et de variance ont un sens). Ils sont parfois appelés éléments homogènes de l'algèbre graduée.
- Les éléments de (avec ) sont généralement appelés tenseurs contravariants, ceux de (avec ) tenseurs covariants et ceux de (avec ) tenseurs mixtes.
- En toute rigueur, l'algèbre n'offre a priori pas de liberté quant à l'ordre des indices covariants et contravariants. Elle ne contient par exemple pas l'espace . Néanmoins on convient généralement qu'un tel espace est, si nécessaire, assimilé à par permutation des indices (les indices contravariants sont décalés vers l'avant au besoin) :
Cette permutation permet d'affirmer que le produit tensoriel est bien une opération interne à .
Ordre
Si et sont des tenseurs respectivement et sur , alors est (sous réserve de permutation des indices) un tenseur .
Un produit contracté (sur des indices à préciser) est un tenseur . D'une manière générale toute opération de contraction diminue la covariance et la contravariance de 1. Elle réduit donc l'ordre de 2.
Trace des endomorphismes
Un endomorphisme de peut être vu comme un élément , autrement dit un tenseur . La trace de cet endomorphisme vaut ; c'est-à-dire le résultat de la contraction de par rapport à ses deux indices.
Symétrie et antisymétrie
Soit un tenseur de et deux indices et correspondant au même espace vectoriel (c'est-à-dire soit soit pour les deux indices).
On dit que est symétrique par rapport aux indices et si .
On dit que est antisymétrique par rapport aux indices et si .
On dit que est totalement symétrique s'il est symétrique pour tout couple d'indice. Il faut donc pour cela qu'il appartienne à ou .
On dit que est totalement antisymétrique s'il est antisymétrique pour tout couple d'indice. Là encore, l'espace doit être ou .
Produit scalaire
Un produit scalaire réel sur un espace de dimension finie sur est un cas particulier de tenseur symétrique qu'on peut noter . Il est par ailleurs défini et positif. On a donc :
Cas des espaces euclidiens et quadratiques
Dans un espace euclidien (ou plus généralement dans un espace quadratiques non-dégénéré) , l'existence d'un produit scalaire réel (respectivement d'un pseudo-produit scalaire, c'est-à-dire d'une forme bilinéaire symétrique non dégénérée ou de manière équivalente d'une forme quadratique non-dégénérée) fournit des propriétés particulières aux tenseurs. Celui-ci permet en effet d'établir un isomorphisme canonique associant une unique forme linéaire à tout vecteur :

Le (pseudo-) produit scalaire sur définit en outre naturellement un (pseudo-) produit scalaire sur . Il s'agit de l'unique élément de , qu'on peut noter , vérifiant pour tout , et pour tout , . L'isomorphisme a pour réciproque .
Assimilation avec le dual
Via l'isomorphisme on peut alors assimiler tout élément de à un élément de : . D'une manière générale, cela permet de ne plus distinguer les indices contravariants et covariants. Dans ces conditions, un tenseur de type peut être aussi bien vu comme un tenseur que . L'ordre devient alors une caractéristique suffisante pour catégoriser tout tenseur construit sur .
Correspondance entre produits scalaire et contracté
Il devient possible de contracter deux vecteurs de . Cette contraction s'identifie au produit scalaire :

Contractions sur des indices quelconques
On peut maintenant contracter deux indices correspondant au même espace quadratique par utilisation implicite du produit scalaire :

À propos des espaces hermitiens
Un produit scalaire hermitien n'est pas un tenseur : il n'est en effet que semi-linéaire par rapport à sa première variable. De fait, les propriétés énoncées ci-dessus ne s'appliquent pas dans le cadre des espaces hermitiens.
Calcul pratique
La manipulation effective des tenseurs nécessite généralement de les représenter dans des bases particulières (mais néanmoins arbitraires). Soit une base de . On notera sa base duale. Alors tout tenseur de peut s'écrire comme une combinaison linéaire de type : Si la base est précisée par avance la donne des scalaires caractérise entièrement le tenseur. Ils représentent les coordonnées du tenseur dans la base considérée. L'ensemble des conventions d'utilisation des coordonnées des tenseurs est appelé convention d'Einstein. Il est possible de mélanger indices covariants et contravariants. Les indices contravariants sont notés en indices supérieurs, les indices covariants en indices inférieurs. Ainsi se décompose dans une base donnée avec les composants .
Il est cependant possible d'interpréter cette même notation utilisant des indices avec un sens intrinsèque (c'est-à-dire sans faire appel aux coordonnées). Il s'agit alors de la notation en indice abstrait.
Liens entre les notations
On se donne les tenseurs suivant :
- Scalaires :
- Vecteurs :
- Covecteurs (formes linéaires) :
- Tenseurs d'ordre 2 :
- Tenseurs d'ordre 3 et plus :
On choisit par ailleurs une base dans . Ce choix induit naturellement celui de la base duale dans . Les tenseurs précédemment définis admettent alors une seule décomposition dans ces bases.
| Propriétés | Notation sans indices | Convention d'Einstein / Notation en indice abstrait |
|---|---|---|
| Produit tensoriel | ||
| Produit contracté | ||
| Contraction | ||
| Permutation d'indices | ||
| Mélange |
Liens entre les notations dans le cas des espaces quadratiques
On considère par ailleurs l'existence du (pseudo-) produit scalaire .
| Propriétés | Notation sans indices | Convention d'Einstein / Notation en indice abstrait |
|---|---|---|
| Produit contracté | ||
| Contraction |
À propos des changements de base
On notera que seule la convention d'Einstein admet des formules de changement de base. En effet, puisqu'elle prend le parti de représenter un tenseur par un jeu de coordonnées dans une base (voire plusieurs bases) prédéfinie, il existe des formules pour déterminer les coordonnées d'un même tenseur dans une nouvelle base (comme ). Les notations sans indices et en indices abstrait étant par définition indépendantes d'un choix de base, elles n'admettent pas d'équivalents pour ces formules.
Références
- car les 2 espaces vectoriels et sont de dimension finie
Annexes
Articles connexes
Liens externes
- Jean Salençon, « Mécanique des milieux continus — tome 1 : concepts généraux », sur Éditions de l'École polytechnique, : voir l'annexe 1 p. 293-339 : Éléments de calcul tensoriel
- Patrick Gros, « Introduction à l’algèbre tensorielle »
Bibliographie
- Laurent Schwartz, Les tenseurs, Hermann, (ISBN 2-7056-1376-5)
- Roger Godement, Cours d'Algèbre, Paris, Hermann, 1966, §21 et en particulier p. 268-269.
- Roger Godement, Analyse Mathématique III. Fonctions analytiques, différentielles et variétés, surfaces de Riemann , Springer, 2001; chapitre IX, p. 139-174 (avec ses digressions historiques et persiflantes).
- Mikhaïl Postnikov, Leçons de géométrie : IIe semestre : Algèbre linéaire et géométrie différentielle, Moscou, Éditions Mir , 1981
- (en) A. I. Kostrikin (en) et Yu I. Manin, Linear Algebra and Geometry, CRC Press, 1989 (ISBN 2881246834)
- Portail des mathématiques