Base (algèbre linéaire)

En mathématiques, une base d'un espace vectoriel V est une famille de vecteurs de V linéairement indépendants et dont tout vecteur de V est combinaison linéaire[1]. En d'autres termes, une base de V est une famille libre de vecteurs de V qui engendre V.

Le même vecteur peut être représenté dans deux bases différentes (flèches violettes et rouges).

Introduction géométrique

(-2,1)=-2(1,0)+(0,1)

.

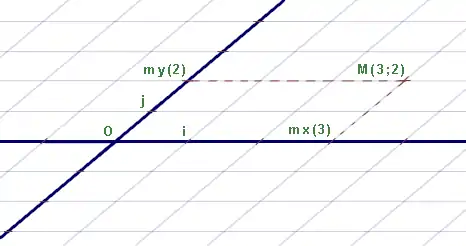
La géométrie plane, celle d'Euclide, peut comporter une approche algébrique, celle de Descartes. En utilisant les coordonnées cartésiennes, on peut identifier un vecteur du plan à un couple de réels. Par exemple, la figure montre comment placer le vecteur ${\overrightarrow {u}}=(-2,1)$ . On se sert alors des deux vecteurs de référence (dessinés en bleu et rouge) pour le dessiner. Ainsi, tous les vecteurs du plan peuvent être exprimés de manière unique en termes de nombres vis-à-vis de deux vecteurs de référence. Ces deux vecteurs sont appelés base canonique du plan. En les notant respectivement ${\overrightarrow {i}}$ et ${\overrightarrow {j}}$ , un vecteur quelconque ${\overrightarrow {v}}$ du plan s'exprime comme combinaison linéaire de ces deux vecteurs :

{\overrightarrow {v}}=x{\overrightarrow {i}}+y{\overrightarrow {j}}

où $x$ et $y$ sont des nombres réels. Par exemple,

{\overrightarrow {u}}=(-2,1)=-2{\overrightarrow {i}}+{\overrightarrow {j}}=-2(1,0)+(0,1)

.

Cette écriture permet d'effectuer des calculs simplement. Par exemple, on peut additionner deux vecteurs ${\overrightarrow {w_{1}}}=x_{1}{\overrightarrow {i}}+y_{1}{\overrightarrow {j}}$ et ${\overrightarrow {w_{2}}}=x_{2}{\overrightarrow {i}}+y_{2}{\overrightarrow {j}}$ (où $x_{1}$ , $x_{2}$ , $y_{1}$ et $y_{2}$ sont des réels) de la façon suivante :

{\overrightarrow {w_{1}}}+{\overrightarrow {w_{2}}}=(x_{1}+x_{2}){\overrightarrow {i}}+(y_{1}+y_{2}){\overrightarrow {j}}

.

Cette addition a une signification géométrique. Ainsi, il existe des connexions entre géométrie et calcul algébrique.

Le couple de vecteurs

(i,j)

est une base du plan.

Cette base n'est pas unique. En fait, n'importe quel couple de vecteurs du plan choisi au hasard forme une base, à condition que les deux vecteurs ne soient pas colinéaires (c'est-à-dire qu'il s'agit d'une famille libre). Les deux vecteurs peuvent alors être utilisés pour exprimer tous les autres vecteurs (c'est-à-dire qu'il s'agit d'une famille génératrice). La décomposition selon ces deux vecteurs est alors unique. La figure ci-contre montre une autre base du plan. Travailler dans d'autres bases que la base canonique permet de simplifier grandement les calculs, si la base choisie est adaptée au problème.

Cette notion de base se généralise à toute structure vectorielle. Cela offre les mêmes avantages que pour les bases du plan, à savoir un cadre simple dans lequel tout vecteur possède une unique écriture, qui facilite les calculs dans cette structure.

Définitions formelles

Soit $E$ un espace vectoriel sur un corps commutatif $K$ .

Famille libre

Une famille finie $(e_{1},\ldots ,e_{n})$ de vecteurs de E est dite libre si :

\forall (\lambda _{1},\ldots ,\lambda _{n})\in K^{n}\ \left(\sum _{i=1}^{n}\lambda _{i}e_{i}=0\Longrightarrow \lambda _{1}=\lambda _{2}=\dots =\lambda _{n}=0\right)

.

Dans le cas contraire, elle est dite liée.

Plus généralement, si $(e_{i})_{i\in I}$ est une famille (éventuellement infinie) de vecteurs de E, cette famille est dite libre si toutes ses sous-familles finies sont libres.

Famille génératrice

Une famille $(e_{1},\ldots ,e_{n})$ finie de vecteurs de $E$ est dite génératrice de $E$ si tout vecteur de $E$ est une combinaison linéaire des vecteurs de cette famille :

\forall x\in E\ \exists (\lambda _{1},\ldots ,\lambda _{n})\in K^{n}\ x=\sum _{i=1}^{n}\lambda _{i}e_{i}

.

Plus généralement, si $(e_{i})_{i\in I}$ est une famille (éventuellement infinie) de vecteurs de $E$ , cette famille est dite génératrice de $E$ si tout vecteur de $E$ est une combinaison linéaire d'une partie finie de la famille $(e_{i})_{i\in I}$ .

Définition d'une base

Une famille de vecteurs de E est une base de E si c'est une famille à la fois génératrice de E et libre[2]. De façon équivalente, une famille est une base de l'espace vectoriel E quand tout vecteur de l'espace se décompose de façon unique en une combinaison linéaire de vecteurs de cette base.

On précise cette dernière caractérisation. Une famille finie $B=(e_{1},\ldots ,e_{n})$ est une base de $E$ si et seulement si :

{\displaystyle \forall x\in E\ \exists

.

Plus généralement, si $B=(e_{i})_{i\in I}$ est une famille (éventuellement infinie) de vecteurs de $E$ , cette famille est une base de $E$ si, pour tout vecteur $x$ de $E$ , il existe une unique famille $(\lambda _{i})_{i\in I}$ de scalaires qui est nulle sauf en un nombre fini d'indices et telle que :

x=\sum _{i\in I}\lambda _{i}e_{i}

.

Les scalaires $\lambda _{i}$ sont appelés coordonnées du vecteur $x$ dans la base $B$ .

Dimension

Qu'elles soient finies ou non, toutes les bases d'un espace vectoriel E ont la même cardinalité, appelée la dimension de E. En particulier, si E admet une famille génératrice finie, toute base de E est finie, et la dimension de E est le nombre de vecteurs qu'elle comprend. Ce résultat, qui justifie la définition de la dimension, porte des noms différents selon les auteurs : théorème de la dimension, théorème d'équicardinalité des bases, etc.

Toute famille libre de E a alors un cardinal inférieur ou égal à dim(E), et toute famille génératrice de cet espace a un cardinal supérieur ou égal à dim(E).

Par exemple, Kⁿ est de dimension n car sa base canonique possède exactement n vecteurs.

Les solutions à l'équation différentielle linéaire d'ordre deux $f''+hf'+k=0$ forment un espace vectoriel réel de dimension 2 : ce résultat s'appuie sur le théorème de Cauchy-Lipschitz.

Exemples

Le ℝ-espace vectoriel ℝ^$n$ admet une base $C$ particulière, appelée base canonique, définie par $C=\{e_{1}=(1,0,\ldots ,0),\ e_{2}=(0,1,\ldots ,0),\ \ldots \ ,e_{n}=(0,0,\ldots ,1)\}$ .La dimension de ℝ^$n$ est donc $n$ .
L'espace vectoriel M_n,p(K) des matrices de taille n×p à coefficients dans un corps K admet pour base l'ensemble formé des matrices élémentaires de M_n,p(K), c'est-à-dire des matrices ayant un coefficient égal à 1 et tous les autres nuls. La dimension de M_n,p(K) est donc np.
L'espace vectoriel des polynômes sur un corps K admet pour base {X^k | k ∈ ℕ} (plus généralement, toute famille de polynômes étagée en degré convient, par exemple si K = ℝ : une suite de polynômes orthogonaux). La dimension de K[X] est donc l'infini dénombrable.

Existence

Tout espace vectoriel admet une base d'après le théorème suivant[3]^,[4] :

Théorème de la base incomplète — Soient E un espace vectoriel, G une partie génératrice de E et L une partie libre. Alors il existe F ⊂ G\L tel que L∪F soit une base de E.

Autrement dit, toute famille libre de E peut toujours être « complétée » pour obtenir une base de E en choisissant des vecteurs parmi une famille génératrice arbitrairement prescrite. En particulier, la famille vide peut être complétée en une base de E.

Ce théorème prouve également qu'une famille de vecteurs est une base (c.-à-d. libre et génératrice) si et seulement si elle est libre maximale ou encore (c'est équivalent) génératrice minimale.

L'existence d'une base pour tout espace vectoriel est équivalente, en théorie des ensembles ZF avec axiome de fondation[5], à l'axiome du choix. En particulier, la démonstration du théorème de la base incomplète repose sur le lemme de Zorn. Cependant, l'existence d'une famille génératrice finie permet de démontrer l'existence d'une base sans invoquer l'axiome du choix.

Changement de base

Il n'y a pas a priori d'unicité d'une base dans un espace vectoriel. Il peut donc être naturel de vouloir passer de l'expression d'un vecteur dans une base donnée à celle dans une autre base, par exemple pour faciliter les calculs.

Soit E un espace vectoriel sur un corps K. On suppose que $(e_{i})_{i\in I}$ et $(e'_{i})_{i\in I}$ sont deux bases de cet espace. Les $e'_{i}$ sont en particulier des vecteurs de E, donc s'expriment comme combinaisons linéaires des vecteurs de la base $(e_{i})$ . On peut donc en déduire, par substitution, les nouvelles expressions des vecteurs.

Par exemple, dans le ℝ-espace vectoriel ℝ², on a la base canonique $(e_{1}=(1,0),e_{2}=(0,1))$ . Il est facile de vérifier que les vecteurs $e'_{1}=(1,1)$ et $e'_{2}=(1,-1)$ forment une base de ℝ². On peut exprimer ces nouveaux vecteurs par

e'_{1}=(1,1)=e_{1}+e_{2}\quad {\text{et}}\quad e'_{2}=(1,-1)=e_{1}-e_{2}

.

Et en résolvant le système d'équations, on obtient

e_{1}={\frac {1}{2}}\left(e_{1}'+e_{2}'\right)\quad {\text{et}}\quad e_{2}={\frac {1}{2}}\left(e_{1}'-e_{2}'\right)

.

Pour un vecteur $x=\lambda _{1}e_{1}+\lambda _{2}e_{2}$ de ℝ² (avec $\lambda _{1}$ et $\lambda _{2}$ des réels), on peut donc l'exprimer en fonction de la nouvelle base :

x=\lambda _{1}e_{1}+\lambda _{2}e_{2}={\frac {\lambda _{1}}{2}}\left(e_{1}'+e_{2}'\right)+{\frac {\lambda _{2}}{2}}\left(e_{1}'-e_{2}'\right)={\frac {\lambda _{1}+\lambda _{2}}{2}}e_{1}'+{\frac {\lambda _{1}-\lambda _{2}}{2}}e_{2}'

.

Application linéaire

Une application linéaire φ d'un espace vectoriel E vers un espace vectoriel F est entièrement déterminée par l'image par φ d'une base de E. Plus précisément : soit $e=(e_{i})_{i\in I}$ une base de E ; pour toute famille $f=(f_{i})_{i\in I}$ de vecteurs de F (indexée par le même ensemble $I$ ), il existe une unique application linéaire $\varphi :E\to F$ telle que $\forall i\in I\quad \varphi (e_{i})=f_{i}$ . De plus, φ est bijective si et seulement si $f$ est une base de F. Cette propriété fournit donc un isomorphisme entre deux K-espaces vectoriels de même dimension (en particulier : un isomorphisme entre E et Kⁿ, si E est de dimension finie n).

En dimension finie, cette propriété permet également d'utiliser des matrices comme représentants des applications linéaires de E dans F, étant données une base e de E et une base f de F. Si F = E, la matrice de l'application identité est appelée la matrice de passage, ou matrice de changement de base, de f (l'« ancienne base ») à e (la « nouvelle base »)[6].

Base d'un espace dual

Soit $E$ un $K$ -espace vectoriel. L'ensemble des formes linéaires sur $E$ forment un $K$ -espace vectoriel appelé espace dual de $E$ noté $E^{*}$ . Si $E$ est de dimension finie, alors $E^{*}$ est aussi de dimension finie et sa dimension est égale à celle de $E$ . Ils sont donc isomorphes.

Si $(e_{1},\ldots ,e_{n})$ est une base de $\ E$ , on définit sur celle-ci les formes linéaires notées $(e_{1}^{*},\ldots ,e_{n}^{*})$ par :

\forall (i,j)\in \{1,\ldots ,n\}^{2}\ e_{i}^{*}(e_{j})=\delta _{i,j}

où $\delta _{ij}$ est le symbole de Kronecker.

La famille de formes linéaires $(e_{1}^{*},\ldots ,e_{n}^{*})$ est une base de $E^{*}$ , appelée base duale de la base $(e_{1},\ldots ,e_{n})$ .

Inversement, si $(f_{1}^{*},\ldots ,f_{n}^{*})$ est une base de $\ E^{*}$ , il existe une unique base $(f_{1},\ldots ,f_{n})$ de $E$ telle que :

\forall (i,j)\in \{1,\ldots ,n\}^{2}\ f_{i}^{*}(f_{j})=\delta _{i,j}

.

La base $(f_{1},\ldots ,f_{n})$ s'appelle la base antéduale de la base $(f_{1}^{*},\ldots ,f_{n}^{*})$ .

Généralisation de la notion de base

Lorsque l'espace vectoriel étudié dispose d'une structure plus riche, un raffinement de la notion de base est possible.

Base orthonormale

Dans le cas d'un espace euclidien, une base est dite orthonormale (ou orthonormée) si les vecteurs de cette base sont deux à deux orthogonaux et sont de norme égale à 1.

Par exemple, la base canonique de $\mathbb {R} ^{n}$ est orthonormale pour le produit scalaire usuel.

Base de Hilbert

Dans un espace préhilbertien de dimension infinie, une famille finie de vecteurs orthogonaux deux à deux ne peut pas engendrer tout l'espace.

Soit $H$ un espace préhilbertien sur un corps $K=\mathbb {R} \ \mathrm {ou} \ \mathbb {C}$ et $F=(e_{i})_{i\in I}$ une famille de vecteurs de $H$ , où l'ensemble $I$ des indices est fini ou infini.

La famille $F$ est une base de Hilbert de $H$ si

$F$ est une famille orthonormée de $H$ et
$F$ est « génératrice », au sens élargi suivant : $\forall x\in H\ \exists (\lambda _{i})_{i\in I}\in K^{I}\ x=\sum _{i\in I}\lambda _{i}e_{i}$ .

Dans le cas où $H$ est de dimension finie, cette définition coïncide avec celle de base orthonormée.

Base de Schauder

Dans le cas où E est un espace de Banach séparable de dimension infinie, on peut généraliser la notion de base dans le sens suivant : on dit que la suite $(e_{n})_{n\in \mathbb {N} }$ de vecteurs de E est une base de Schauder de E si, pour tout $x\in E$ , il existe une unique suite $(a_{n})_{n\in \mathbb {N} }$ de scalaires telle que

x=\lim _{n}\sum _{k=0}^{n}a_{k}e_{k}

,

avec convergence en norme dans E. Les scalaires $(a_{n})_{n\in \mathbb {N} }$ sont appelés coordonnées de $x$ .

Une base de Hilbert (séparable) est une base de Schauder. Dans le cas où E est de dimension finie, les notions de base (algébrique) et base de Schauder coïncident.

Base d'un module

Un module est une structure algébrique identique à celle d'espace vectoriel à la différence près que l'ensemble des scalaires ne forme plus un corps mais un anneau.

Certaines propriétés vraies pour les espaces vectoriels ne sont plus vraies pour les modules. Par exemple l'existence d'une base n'y est plus assurée, même dans un module engendré par un nombre fini d'éléments. Il est même possible qu’un tel module admette un sous-module qui ne soit pas finiement engendré.

Cependant, on peut quand même définir une notion de base, identique à celle des espaces vectoriels. Un module qui possède une base s'appelle un module libre, mais le cardinal de ses bases n’est pas nécessairement une constante.

Références

(en) Eric W. Weisstein, « Vector Basis », sur MathWorld.
(en) Serge Lang, Algebra [détail des éditions], 1965, p. 84.
N. Bourbaki, Algèbre, p. A-II-95, Théorème 2.
Lang 1965, p. 85, Theorem 2.
(en) Andreas Blass (en), « Existence of bases implies the axiom of choice », dans J. E. Baumgartner, D. A. Martin et S. Shelah, Axiomatic Set Theory, coll. « Contemp. Math. » (n^o 31), 1984, p. 31-34.
Daniel Guinin et Bernard Joppin, Algèbre et géométrie PCSI, Bréal, 2003 (lire en ligne), p. 356.

Portail de l’algèbre

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Eric W. Weisstein, « Vector Basis », sur MathWorld.

[2] (en) Serge Lang, Algebra [détail des éditions], 1965, p. 84.

[3] N. Bourbaki, Algèbre, p. A-II-95, Théorème 2.

[4] Lang 1965, p. 85, Theorem 2.

[5] (en) Andreas Blass (en), « Existence of bases implies the axiom of choice », dans J. E. Baumgartner, D. A. Martin et S. Shelah, Axiomatic Set Theory, coll. « Contemp. Math. » (n^o 31), 1984, p. 31-34.

[6] Daniel Guinin et Bernard Joppin, Algèbre et géométrie PCSI, Bréal, 2003 (lire en ligne), p. 356.