Octogone
Un octogone (du grec ὀκτάγωνον oktágōnon, cf. ὀκτώ oktṓ « huit » et γωνία gōnía « angle ») est un polygone à huit sommets, donc huit côtés et vingt diagonales.
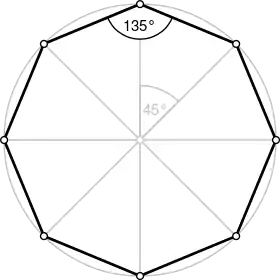
| Octogone régulier | |
| |
| Type | Polygone régulier |
|---|---|
| Arêtes | 8 |
| Sommets | 8 |
| Symbole de Schläfli | {8} |
| Diagramme de Coxeter-Dynkin | |
| Groupe de symétrie | Groupe diédral D16 |
| Angle interne | 135° |
| Propriétés | Constructible |
La somme des angles internes d'un octogone non croisé est égale à 6π rad, soit 1 080°.
Octogone régulier
Un octogone régulier est un octogone dont les huit côtés ont la même longueur et dont les angles internes ont même valeur.
Il existe un octogone régulier étoilé (l'octagramme régulier, noté {8/3}) mais usuellement, « octogone régulier » désigne implicitement l'octogone régulier convexe, noté {8}.
Propriétés
Pour un octogone régulier de côté a :
- l'angle interne vaut 3π/4 rad, soit 135° ;
- le rayon du cercle circonscrit est
- le rayon du cercle inscrit et donc la longueur de l'apothème est(cot est ici la fonction cotangente) ;
- le périmètre est égal à 8a ;
- l'aire est égale àElle vaut également
Construction
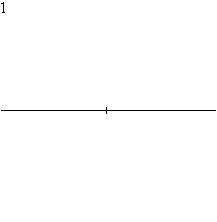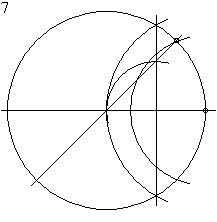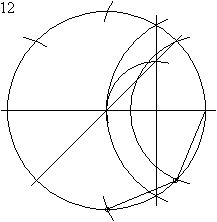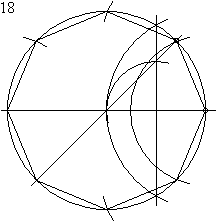
D'après le théorème de Gauss-Wantzel et puisque 8 est une puissance de 2, l'octogone régulier est constructible à la règle et au compas. La construction suivante est possible :
- 1 : tracer une droite.
- 2 : tracer un cercle dont le centre est situé sur la droite.
- 3 : tracer un arc de cercle dont le centre est situé à l'intersection de la droite et du cercle précédent, de même rayon que celui-ci.
- 4 : tracer une droite passant par les deux points où les cercles se coupent.
- 5 : tracer un arc de cercle ayant pour centre l'intersection des deux droites et passant par le centre du premier cercle.
- 6 : tracer une droite passant par l'intersection de la dernière droite et du dernier cercle, et par le centre du cercle tracé en 2.
- 7 : l'intersection avec le cercle donne la distance à reporter pour chaque côté de l'octogone
- 8 à 10 : reporter les côtés.
- 11 à 18 : tracer l'octogone.
Ou plus simplement :
- Tracer un carré, tracer les diagonales.
- Reporter la demi-diagonale sur les côtés du carré à partir de chaque angle.
- Tracer l'octogone en coupant les coins du carré.
Architecture
Dans la région méditerranéenne, différents monuments et bassins ont été construit sur une forme octogonale: Plusieurs monuments furent construits selon un plan octogonal, parmi lesquels la tour des Vents à Athènes (Ier ou IIe siècle av. J.-C.), le dôme du Rocher à Jérusalem (VIIe siècle), ou encore Castel del Monte en Apulie, conçu par l'empereur Frédéric II du Saint-Empire au XIIIe siècle. Castel del Monte offre la particularité de se présenter comme un château octogonal flanqué de huit tours octogonales.
La tour des Vents d'Athènes a inspiré celle d'autres monuments : la Torre del Marzocco à Livourne (XVe siècle), l'observatoire Radcliffe à Oxford (XVIIIe siècle), le mausolée de Panayis Vagliano (de), fondateur de la Bibliothèque nationale de Grèce (cimetière de West Norwood, Londres), ou la Tour des vents de Sébastopol, édifiée en 1849.

Las bassins octogonaux se trouvent occasionnellement dans certains monuments anciens comme des églises ou des hammams Palais impérial de Rome, le Baptistère du Latran, ou le hammam d'Amir Ahmad.
Pour les alchimistes, l'octogone est le parfait mélange entre le carré (l'Humain) et le cercle (le Divin).
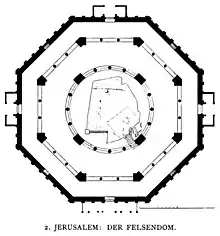 Plan du dôme du Rocher.
Plan du dôme du Rocher.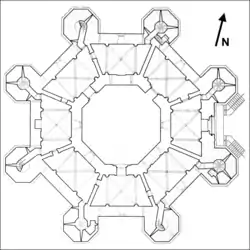 Plan de Castel del Monte.
Plan de Castel del Monte. Octagonal Lodge (Pennsylvanie, États-Unis).
Octagonal Lodge (Pennsylvanie, États-Unis).
Notes et références
Voir aussi
Articles connexes
- Table de lignes trigonométriques exactes
- Octogone de Montmorillon : chapelle romane
- Panneau stop, panneau de signalisation octogonal
Liens externes
- (en) Eric W. Weisstein, « Octagon », sur MathWorld
- (en) Eric W. Weisstein, « Trigonometry Angles — Pi/8 », sur MathWorld
- Portail de la géométrie