Cercle circonscrit
En géométrie, un cercle circonscrit à un polygone est un cercle qui passe par tous les sommets du polygone. Le polygone est alors dit inscrit dans le cercle : on parle de polygone inscriptible. Les sommets sont alors cocycliques, situés sur un même cercle. Ce cercle est unique et son centre est le point d'intersection des médiatrices des côtés.
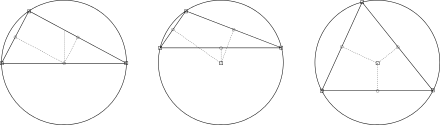
Cas particuliers
Triangle
Tout triangle est inscriptible.
Rayon du cercle
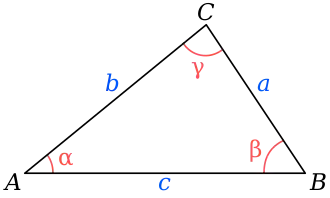
On considère un triangle non plat ABC, où les angles sont désignés par les minuscules grecques et les côtés opposés aux angles par la minuscule latine correspondante :
- a = BC et α, l'angle formé par [AB] et [AC] ;
- b = AC et β, l’angle formé par [BA] et [BC] ;
- c = BA et γ, l’angle formé par [CA] et [CB].
R est le rayon du cercle circonscrit.
Alors, d'après la loi des sinus, on a :
Ce qui permet de déterminer le rayon du cercle circonscrit :
Triangle rectangle
- Le cercle circonscrit à un triangle rectangle a la particularité d'admettre pour diamètre l'hypoténuse de ce triangle rectangle. Le centre du cercle circonscrit se trouve donc au milieu de l'hypoténuse. Son rayon vaut :
- Tout triangle inscrit dans un cercle et dont le plus long côté est un diamètre de ce cercle est un triangle rectangle, d'après le théorème de Thalès sur le cercle.
Remarque : avec ces notations, une équation barycentrique du cercle circonscrit à ce triangle est
- .
Triangle tangentiel
Pour un triangle ABC, de cercle circonscrit (c), les tangentes à (c) en A, B, C forment un triangle T1T2T3 dit tangentiel de ABC.
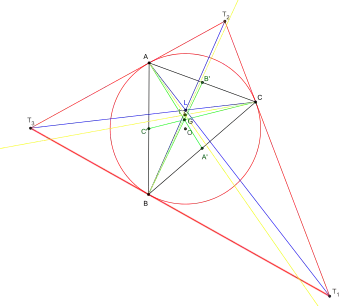
Les symédianes joignent les sommets du triangle aux sommets du triangle tangentiel.
Elles sont concourantes et leur point de concours est le point de Lemoine.
Quadrilatère
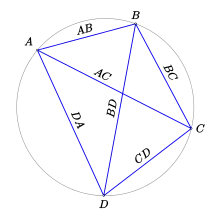
Un quadrilatère est inscriptible si, et seulement si, deux angles opposés sont égaux ou supplémentaires :
- un quadrilatère croisé est inscriptible si, et seulement si, deux angles opposés sont égaux.
- un quadrilatère convexe est inscriptible si, et seulement si, deux angles opposés sont supplémentaires.
Théorème de Ptolémée : un quadrilatère convexe est inscriptible si, et seulement si, le produit des longueurs des diagonales est égal à la somme des produits des longueurs des côtés opposés
Rectangle
Tout rectangle (et donc tout carré) possède un cercle circonscrit dont le centre se trouve à l'intersection de ses diagonales, et dont le rayon vaut, comme pour le triangle rectangle :
Pour le cas du carré, Longueur = largeur donne :
Cette propriété dérive de celle du triangle, par symétrie.
Losange
Un losange qui n'est pas un carré ne possède pas de cercle circonscrit.
Parallélogramme
Un parallélogramme qui n'est pas un rectangle ne possède pas de cercle circonscrit.
Hexagone régulier
L'hexagone régulier est circonscrit par un cercle de rayon mesurant la longueur d'un côté.
Cette propriété permet de tracer facilement un hexagone régulier avec une règle et un compas.
Bibliographie
Voir aussi
- Cercle inscrit
- Cercle d'Euler
- Polygone bicentrique (en)
- Porisme de Poncelet
- Sphère circonscrite
- Portail de la géométrie