Cercle inscrit
En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon possible inclus dans la surface.
Existence
Pour qu'un polygone possède un unique cercle inscrit, il faut que ses bissectrices soient concourantes. Si c'est le cas, le point d'intersection est le centre du cercle inscrit.
Cas particuliers
Triangle
Tout triangle non plat possède un unique cercle inscrit.
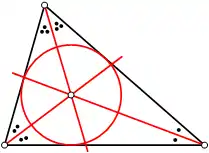
Cercle inscrit dans un triangle
Bibliographie
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Méthodes modernes en géométrie de Jean Fresnel
- Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)
Voir aussi
- Cercle circonscrit
- Cercle d'Euler
- Liste des éléments remarquables d'un triangle
- Cercle de Conway
- Théorème de Pitot
- Triangle rectangle
- Porisme de Poncelet
- Sphère inscrite
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.