Force de Lorentz

Champ magnétique créé par des bobines de Helmholtz.

Le champ électromagnétique exerce la force suivante sur des particules possédant une charge électrique q non nulle

${\displaystyle {\vec {F}}=q{\vec {E}}+q{\vec {v}}\wedge {\vec {B}}}$.

Les vecteurs ${\displaystyle {\vec {E}}}$ et ${\displaystyle {\vec {B}}}$ sont respectivement le champ électrique et le champ magnétique pris au point où se trouve la particule, ${\displaystyle {\vec {v}}}$ représente la vitesse de la particule dans le référentiel d'étude. On peut distinguer deux contributions à cette force :

• ${\displaystyle {\vec {F_{\text{el}}}}=q{\vec {E}}}$, qui est la force électrique ;
• ${\displaystyle {\vec {F_{\text{mag}}}}=q{\vec {v}}\wedge {\vec {B}}}$, qui est la force magnétique.

Dans le cas où la charge électrique est immobile à une certaine position nommée ${\displaystyle {\vec {r}}'}$, sa vitesse est donc nulle, et elle n'est pas soumise à une quelconque force magnétique : le produit vectoriel ${\displaystyle {\vec {v}}\wedge {\vec {B}}}$ est nul, et la charge est alors soumise à une force qui ne dépend que du champ électrique ${\displaystyle {\vec {E}}}$.

${\displaystyle {\vec {F}}={\vec {F_{\text{el}}}}=q{\vec {E}}}$.

Action de la force de Lorentz dans le cas d'un champ électrique nul.

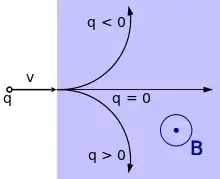
Le champ électrique s'exerçant en ${\displaystyle {\vec {r}}}$ est alors donné par la loi de Coulomb :

${\displaystyle {\vec {E}}={\frac {q}{4\pi \varepsilon _{0}}}{\frac {{\vec {r}}-{\vec {r'}}}{|{\vec {r}}-{\vec {r'}}|^{3}}}}$,

ε₀ est une constante universelle appelée la permittivité du vide (à remplacer par la permittivité du milieu, lorsqu'on n'est pas dans le vide).

Le calcul de la force ne se fait que lorsque l'on connaît la valeur des champs ${\displaystyle {\vec {E}}}$ et ${\displaystyle {\vec {B}}}$, qui sont principalement déterminés par la distribution de l'ensemble des particules chargées intervenant dans la configuration étudiée.

Cette section ne cite pas suffisamment ses sources (mai 2021). 

Pour l'améliorer, ajoutez des références vérifiables [comment faire ?] ou le modèle {{Référence nécessaire}} sur les passages nécessitant une source.

Historiquement, la force de Lorentz était une donnée indépendante de l'équation décrivant le champ électromagnétique. On peut retrouver la force de Lorentz grâce au formalisme lagrangien. Le lagrangien permettant de retrouver les équations de Maxwell permet également de retrouver la force de Lorentz. Les équations de Maxwell sont les équations sources, et la force de Lorentz est l'équation d'évolution (équation dynamique). On retrouve les deux grâce aux équation d'Euler-Lagrange. Pour retrouver les équations dynamiques on applique les équations d'Euler-Lagrange aux coordonnées d'espaces (positions, vitesses), et pour retrouver les équations sources (équation de Maxwell), on applique les équations d'Euler-Lagrange aux coordonnées généralisées (champs, et dérivées du champ). L'action d'une particule chargée ponctuelle soumise à un champ électrique est :

${\displaystyle S=\int _{t_{1}}^{t_{2}}\left(-mc^{2}{\sqrt {1-{\tfrac {{\vec {V}}^{2}}{c^{2}}}}}-q\phi +q{\vec {A}}\cdot {\vec {V}}\right)dt}$.

avec

${\displaystyle S=\int _{t_{1}}^{t_{2}}L\,dt}$.

Pour appliquer les équations d'Euler-Lagrange, on cherche donc d'abord le moment :

${\displaystyle \Pi ={\frac {\partial L}{\partial {\vec {V}}}}={\frac {m{\vec {V}}}{\sqrt {1-{\frac {{\vec {V}}^{2}}{c^{2}}}}}}+q{\vec {A}}}$

La notation ${\displaystyle {\frac {\partial L}{\partial {\vec {V}}}}}$ étant un peu abusive. L'équation d'Euler-Lagrange nous dit alors que :

${\displaystyle {\frac {d\Pi }{dt}}={\frac {d({\vec {P}}+q{\vec {A}})}{dt}}={\frac {\partial L}{\partial {\vec {x}}}}=-q\nabla \phi +q\nabla ({\vec {A}}.{\vec {V}})}$.

et

${\displaystyle {\frac {d{\vec {A}}}{dt}}={\frac {\partial {\vec {A}}}{\partial t}}+({\vec {V}}.\nabla ){\vec {A}}}$.

donc

${\displaystyle {\frac {d{\vec {P}}}{dt}}+q{\frac {\partial {\vec {A}}}{\partial t}}+q({\vec {V}}.\nabla ){\vec {A}}=-q\nabla \phi +q\nabla ({\vec {A}}.{\vec {V}})}$.

Et en utilisant l'identité vectorielle

${\displaystyle {\vec {V}}\wedge (\nabla \wedge {\vec {A}})=\nabla ({\vec {A}}\cdot {\vec {V}})-({\vec {V}}\cdot \nabla ){\vec {A}}}$.

on obtient

${\displaystyle {\frac {d{\vec {P}}}{dt}}=-q{\frac {\partial {\vec {A}}}{\partial t}}-q\nabla \phi +q\left({\vec {V}}\wedge (\nabla \wedge {\vec {A}})\right)}$.

soit la force de Lorentz si

${\displaystyle \nabla \wedge {\vec {A}}={\vec {B}}}$.

et

${\displaystyle {\vec {E}}=-\nabla \phi -{\frac {\partial {\vec {A}}}{\partial t}}}$.

On peut également faire apparaitre la force de Lorentz grâce aux équations de Maxwell, elle apparait comme terme source dans l'équation de continuité de la densité d'impulsion du champ électromagnétique. Soit

${\displaystyle {\frac {\partial ({\vec {E}}\wedge {\vec {B}})}{\mu _{0}\partial t}}+\rho {\vec {E}}+{\vec {j}}\wedge {\vec {B}}-\nabla \sigma =0}$.

avec ${\displaystyle \sigma }$ le tenseur des contraintes de Maxwell.

On peut aussi passer par le formalisme relativiste du lagrangien, appliqué à la relativité restreinte. Dans ce cadre-là, le mouvement d'une particule suivant la trajectoire x^b(τ) soumise au champ électromagnétique est décrit par son action, qui prend la forme ${\displaystyle S=\int qA_{b}\;{\rm {d}}x^{b}}$, où la quantité A_i est ce que l'on appelle le quadripotentiel, duquel on tire le potentiel électrique et le potentiel vecteur qui déterminent entièrement le champ électrique et le champ magnétique.

On définit comme de coutume en relativité restreinte la quadrivitesse par

${\displaystyle u^{a}\equiv {\frac {\rm {dx^{a}}}{\rm {d\tau }}}\quad ,}$

ce qui permet de réécrire l'action sous la forme

${\displaystyle S=\int qA_{b}u^{b}\;{\rm {d}}\tau }$.

Dans le formalisme de l'action (qui est l'intégrale du lagrangien), la trajectoire est déterminée par la maximisation de l'action par rapport aux variations possibles de la trajectoire x^b(τ). La trajectoire apparaît explicitement dans le quadrivecteur vitesse, mais aussi implicitement dans le quadripotentiel, puisque l'on évalue celui-ci en chaque point de la trajectoire. Ainsi, la variation de l'action donne-t-elle

${\displaystyle \delta S=\int q\left(A_{b}{\frac {{\rm {d}}\delta x^{b}}{{\rm {d}}\tau }}+\delta x^{a}\partial _{a}A_{b}u^{b}\right)\;{\rm {d}}\tau }$.

On peut intégrer le premier terme par partie, pour obtenir

${\displaystyle \delta S=\int q\left(-{\frac {{\rm {d}}A_{b}}{{\rm {d}}\tau }}\delta x^{b}+\delta x^{a}\partial _{a}A_{b}u^{b}\right)\;{\rm {d}}\tau }$,

mais comme le quadripotentiel dépend est uniquement évalué sur des points de la trajectoires, on a

${\displaystyle \delta S=\int q\left(-u^{a}\partial _{a}A_{b}\delta x^{b}+\delta x^{a}\partial _{a}A_{b}u^{b}\right)\;{\rm {d}}\tau }$.

En regroupant l'ensemble des termes, il vient

${\displaystyle \delta S=\int q\left((\partial _{a}A_{b}-\partial _{b}A_{a})u^{b}\right)\;\delta x^{a}\;{\rm {d}}\tau }$.

Le terme de l'intégrale en dehors du dτ et des δx^a donne la force. En introduisant le tenseur électromagnétique F_ab tel que

${\displaystyle F_{ab}=\partial _{a}A_{b}-\partial _{b}A_{a}}$,

la force f^a s'écrit donc

${\displaystyle f^{a}=qF_{\;\;b}^{a}u^{b}}$.

Du fait de la structure des équations de Maxwell, on montre que le champ magnétique peut être écrit sous la forme du rotationnel d'un vecteur, le potentiel vecteur du champ magnétique. Or la partie spatiale du tenseur électromagnétique peut s'écrire, si l'on se place en coordonnées cartésiennes x, y, z,

${\displaystyle F_{\;\;b}^{a}=\left({\begin{array}{cccc}0&?&?&?\\?&0&\partial _{x}A^{y}-\partial _{y}A^{x}&\partial _{x}A^{z}-\partial _{z}A^{x}\\?&\partial _{y}A^{x}-\partial _{x}A^{y}&0&\partial _{y}A^{z}-\partial _{z}A^{y}\\?&\partial _{z}A^{x}-\partial _{x}A^{z}&\partial _{z}A^{y}-\partial _{y}A^{z}&0\end{array}}\right)=\left({\begin{array}{cccc}0&?&?&?\\?&0&({\rm {rot}}\;A)^{z}&-({\rm {rot}}\;A)^{y}\\?&-({\rm {rot}}\;A)^{z}&0&({\rm {rot}}\;A)^{x}\\?&({\rm {rot}}\;A)^{y}&-({\rm {rot}}\;A)^{x}&0\end{array}}\right)}$.

Appliqué à la partie spatiale de la quadrivitesse, on vérifie, en notant ${\displaystyle {\vec {B}}}$ le rotationnel de ${\displaystyle {\vec {A}}}$, que l'on a

${\displaystyle F_{\;\;b}^{a}u^{b}=\left({\begin{array}{c}?\\v^{y}B^{z}-v^{z}B^{y}\\v^{z}B^{x}-v^{x}B^{z}\\v^{x}B^{y}-v^{y}B_{x}\end{array}}\right)+...=\left({\begin{array}{c}?\\\\{\vec {v}}\wedge {\vec {B}}\\~\end{array}}\right)}$.

Si maintenant on considère en sus les composantes temporelles du tenseur F, on a

${\displaystyle F_{\;\;b}^{a}=\left({\begin{array}{cccc}0&&-{\frac {1}{c^{2}}}\partial _{t}{\vec {A}}-{\vec {\nabla }}A^{t}&\\&0&B^{z}&-B^{y}\\-{\vec {\nabla }}A_{t}-\partial _{t}{\vec {A}}&-B^{z}&0&B^{x}\\&B^{y}&-B^{x}&0\end{array}}\right)}$.

Or, étant données les équations de Maxwell, on sait que l'on peut écrire le champ électrique comme la somme de l'opposé de la dérivée temporelle du potentiel vecteur et du gradient du potentiel électrique, que l'on va assimiler à A_t. On a ainsi l'expression quadridimensionnelle de la force :

${\displaystyle F_{\;\;b}^{a}u^{b}=\left({\begin{array}{c}{\frac {{\vec {E}}\cdot {\vec {v}}}{c^{2}}}\\\\{\vec {E}}+{\vec {v}}\wedge {\vec {B}}\\~\end{array}}\right)}$.

L'interaction électromagnétique est la deuxième des quatre interactions élémentaires dans l'ordre des puissances. À basse énergie, soit celle des réactions chimiques ou nucléaires, elle est à peu près cent fois plus faible que l'interaction forte, mais dépasse les interactions faibles et gravitationnelles d'un facteur 10¹¹ et 10⁴² respectivement. A l'exception des phénomènes gravitationnels, l'interaction électromagnétique est responsable, à l'échelle atomique, de la plupart des phénomènes observables à l'échelle macroscopique. En effet, à l'échelle macroscopique, l'interaction électromagnétique empêche un objet d'en traverser un autre, permet à un objet d'appliquer une force sur un autre (principe d'action-réaction) ou encore est responsable des forces de frottement.

Le travail de la force de Lorentz correspond à l'énergie transmise par le champ électromagnétique aux particules chargées.
Pour un déplacement élémentaire ${\displaystyle d{\vec {\ell }}}$ du point d'application de la force, le travail élémentaire de la force de Lorentz ${\displaystyle {\vec {F}}}$ est par définition :

${\displaystyle \delta W={\vec {F}}\cdot d{\vec {\ell }}}$

${\displaystyle \delta W=(q{\vec {E}}+q{\vec {v}}\wedge {\vec {B}})\cdot d{\vec {\ell }}}$

Comme on a par définition ${\displaystyle d{\vec {\ell }}={\vec {v}}dt}$, il vient :

${\displaystyle \delta W=q{\vec {E}}\cdot {\vec {v}}dt+q{\vec {v}}\wedge {\vec {B}}\cdot {\vec {v}}dt}$

Le deuxième terme s'annule, le vecteur produit ${\displaystyle {\vec {v}}\wedge {\vec {B}}}$ étant orthogonal à ${\displaystyle {\vec {v}}}$. On trouve donc finalement :

${\displaystyle \delta W=q{\vec {E}}\cdot {\vec {v}}dt}$

Le travail de la force de Lorentz n'est donc pas nul dans le cas général. On constate en revanche que la force magnétique ne travaille pas, seule la composante électrique travaille et peut donc faire varier l'énergie cinétique d'une particule chargée.