Algèbre géométrique (structure)

Avec cette définition, l'algèbre géométrique, le corps et le sous-espace vectoriel sont notés respectivement ${\displaystyle {\mathcal {G}}}$, ${\displaystyle \mathbb {K} }$ et ${\displaystyle {\mathcal {V}}}$.

Hestenes a exprimé sa forte réticence à considérer le cas d'une algèbre sur le corps des complexes[3]. En fait, dans Hestenes, Li et Rockwood 2001, le corps des scalaires est bel et bien choisi égal au corps des réels. La définition la plus générale a ici été présentée mais dans le reste de cet article, sauf mention contraire, on supposera ${\displaystyle \mathbb {K} =\mathbb {R} }$. Dans ce même ouvrage, Hestenes impose aussi à ${\displaystyle {\mathcal {V}}}$ une dimension finie n. Dans ce cas, ${\displaystyle {\mathcal {V}}}$ et ${\displaystyle {\mathcal {G}}}$ peuvent être notés respectivement ${\displaystyle {\mathcal {V}}^{n}}$ et ${\displaystyle {\mathcal {G}}_{n}}$ (ou ${\displaystyle {\mathcal {G}}({\mathcal {V}}^{n})}$).

Dans cet article, ${\displaystyle {\mathcal {V}}}$ est de dimension quelconque, mais dans le cas où cette dimension est infinie, elle sera tout de même supposée dénombrable pour faciliter les notations.

L'opération de multiplication dans une algèbre géométrique est appelée produit géométrique.

Lorsque ${\displaystyle {\mathcal {V}}}$ est de dimension finie, et que le carré de tout élément de ${\displaystyle {\mathcal {V}}}$ est positif, on parle, pour des raisons justifiées plus loin, de « cas euclidien ».

La donnée d'un espace vectoriel ${\displaystyle {\mathcal {V}}}$ et d'une forme quadratique ${\displaystyle {\mathcal {Q}}}$ sur ${\displaystyle {\mathcal {V}}}$ permet de construire une algèbre géométrique dite générée par ${\displaystyle {\mathcal {V}}}$ sous la condition ${\displaystyle v^{2}={\mathcal {Q}}(v)}$. Cette algèbre est ce qu'on appelle l'algèbre de Clifford.

Si une algèbre de Clifford requiert une forme quadratique pour sa définition, on verra plus loin qu'inversement, une algèbre géométrique permet de définir de façon unique une forme quadratique à partir du produit géométrique. La notion d'algèbre géométrique est donc identique à celle d'algèbre de Clifford, la seule différence étant l'ordre de présentation : une algèbre de Clifford est définie à partir d'un espace vectoriel et d'une forme quadratique, tandis qu'une algèbre géométrique est définie à partir d'une algèbre et d'un sous-espace vectoriel particulier. C'est pourquoi de nombreuses sources définissent purement et simplement les algèbres géométriques comme des algèbres de Clifford, assimilant exactement les deux concepts.

Même si ${\displaystyle {\mathcal {G}}}$ est doté d'une structure d'espace vectoriel, David Hestenes réserve le mot vecteur aux éléments de ${\displaystyle {\mathcal {V}}}$. Dans cet article, en règle générale, les vecteurs seront notés en bas-de-casse gras.

Un vecteur de carré nul est dit nul. Parfois, le terme est réservé aux vecteurs différents de zéro, c'est-à-dire aux vecteurs non trivialement nuls.

La signature d'un vecteur a non nul est le signe de a².

La grandeur ou norme d'un vecteur a notée |a|, est le réel positif

${\displaystyle |\mathbf {a} |={\sqrt {|\mathbf {a} ^{2}|}},}$

où |a²| désigne la valeur absolue du réel a² (ou le module du complexe, dans le cas ${\displaystyle \mathbb {K} =\mathbb {C} }$).

À partir du produit géométrique de deux vecteurs a et b, on définit deux nouveaux produits, dont le premier est symétrique et le second antisymétrique[4]:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &={\frac {1}{2}}\left(\mathbf {a} \mathbf {b} +\mathbf {b} \mathbf {a} \right)\\\mathbf {a} \wedge \mathbf {b} &={\frac {1}{2}}\left(\mathbf {a} \mathbf {b} -\mathbf {b} \mathbf {a} \right)\end{aligned}}}$

a • b est appelé produit intérieur, a ∧ b est appelé produit extérieur. La littérature scientifique francophone utilise aussi le symbole ∧ pour désigner le produit vectoriel. Cette ambiguïté n'existe pas dans la littérature anglo-saxonne car le produit vectoriel y est désigné par le symbole ×.

Théorème — Le produit intérieur de deux vecteurs est un scalaire

${\displaystyle \mathbf {a} \cdot \mathbf {b} \in \mathbb {K} }$

.

Le produit extérieur est généralisé à k vecteurs par la formule suivante :

${\displaystyle \bigwedge _{j=1}^{k}\mathbf {a} _{j}=\mathbf {a} _{1}\wedge \mathbf {a} _{2}\wedge \dots \wedge \mathbf {a} _{k}={\frac {1}{k!}}\sum _{\sigma \in {\mathfrak {S}}_{k}}\operatorname {sgn} (\sigma )\mathbf {a} _{\sigma (1)}\mathbf {a} _{\sigma (2)}\dots \mathbf {a} _{\sigma (k)}}$

où ${\displaystyle {\mathfrak {S}}_{k}}$ est le groupe des permutations d'indice k.

La plupart des auteurs attribuent aux produits intérieur et extérieur une priorité supérieure au produit géométrique, de telle sorte que :

${\displaystyle {\begin{aligned}\mathbf {a} \mathbf {b} \cdot \mathbf {c} =\mathbf {a} (\mathbf {b} \cdot \mathbf {c} )\\\mathbf {a} \cdot \mathbf {b} \mathbf {c} =(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} \\\mathbf {a} \mathbf {b} \wedge \mathbf {c} =\mathbf {a} (\mathbf {b} \wedge \mathbf {c} )\\\mathbf {a} \wedge \mathbf {b} \mathbf {c} =(\mathbf {a} \wedge \mathbf {b} )\mathbf {c} \end{aligned}}}$

Pour deux vecteurs a et b, on a la relation suivante, qui constitue la décomposition dite canonique du produit géométrique de deux vecteurs :

${\displaystyle \mathbf {ab} =\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} .}$

${\displaystyle \mathbf {a} \cdot \mathbf {b} }$ et ${\displaystyle \mathbf {a} \wedge \mathbf {b} }$ sont respectivement appelés (pour des raisons justifiées plus loin) partie scalaire et partie bivectorielle du produit géométrique ab.

Deux vecteurs dont le produit intérieur est le scalaire 0 sont dits orthogonaux.

Une famille de vecteurs (e₁, e₂, ...) est dite orthonormée lorsque :

où le scalaire δ_ij est le symbole de Kronecker.

Lorsque cette famille est aussi génératrice de ${\displaystyle {\mathcal {V}}}$, on dit qu'elle constitue une base orthonormée des vecteurs de l'algèbre géométrique ou, avec un léger abus de langage, une base orthonormée de l'algèbre géométrique.

On verra plus loin que dans le cas euclidien, cette définition d'une base orthonormée coïncide avec la définition d'une base orthonormée dans un espace euclidien.

Une lame[5] A_k est un élément de l'algèbre géométrique, qui peut être écrit comme produit extérieur de k vecteurs linéairement indépendants.

${\displaystyle A_{k}=\bigwedge _{j=1}^{k}\mathbf {a} _{j}}$

L'entier k est ce qu'on appelle le grade[6] de A_k.
Ainsi, les scalaires (A₀), les vecteurs (A₁), les bivecteurs (A₂), les trivecteurs (A₃), et en général les k-vecteurs, ont respectivement les grades 0, 1, 2, 3, k.

Deux lames colinéaires sont dites de même orientation lorsque le coefficient de proportionnalité qui les relie est positif. Dans le cas contraire, elles sont dites d'orientation opposée.

Une lame de grade k est dite unitaire (ou unité) lorsqu'elle peut être écrite comme produit géométrique de k vecteurs orthogonaux de grandeur 1.

Une lame est dite dégénérée ou nulle lorsque son carré géométrique est nul.

Les vecteurs (a₁, a₂, ..., a_k) constituent ce qu'on appelle une trame (frame, ou base) de A_k.

On dit aussi que A_k est le pseudoscalaire pour cette trame.

Pour toute trame (a₁, a₂, ..., a_k) , la trame duale est la famille de k vecteurs (a¹, a², ..., a^k) telle que :

${\displaystyle \mathbf {a} ^{i}\cdot \mathbf {a} _{j}=\delta _{j}^{i}.}$

L'indice haut ici ne représente pas l'exponentiation géométrique.

Les termes bivecteur, trivecteur et k-vecteur[7] désignent respectivement des lames de grade deux, trois et k. Certains auteurs[8] distinguent cependant les k-vecteurs des k-lames en stipulant que les k-vecteurs sont les sommes de k-lames. Ces sommes forment un sous-espace vectoriel de ${\displaystyle {\mathcal {G}}}$, noté ${\displaystyle {\mathcal {G}}^{k}}$[9]. Ainsi, ${\displaystyle {\mathcal {G}}^{1}={\mathcal {V}}}$.

Les bivecteurs et trivecteurs peuvent aussi être qualifiés respectivement d'aire orientée et de volume orienté.

Les sous-espaces ${\displaystyle {\mathcal {G}}^{k}}$ constituent une décomposition en somme directe de l'espace géométrique :

${\displaystyle {\mathcal {G}}=\bigoplus _{k}{\mathcal {G}}^{k}}$

Cette décomposition, pour un ${\displaystyle M\in {\mathcal {G}}}$, s'écrit :

${\displaystyle M=\sum _{k}\langle M\rangle _{k}}$

définissant ainsi l'opérateur ${\displaystyle M\mapsto \langle M\rangle _{k}}$ dit de projection au grade k. ${\displaystyle \langle M\rangle _{k}}$ est qualifié de composante de grade k de M, ou encore partie de grade k de M. La partie de grade 0, ou partie scalaire, est également notée ${\displaystyle \langle M\rangle }$.

Les produits intérieur et extérieur d'un r-vecteur A_r et d'un s-vecteur B_s peuvent être définis par :

${\displaystyle {\begin{aligned}A_{r}\cdot B_{s}&=\langle A_{r}B_{s}\rangle _{|r-s|}\\A_{r}\wedge B_{s}&=\langle A_{r}B_{s}\rangle _{r+s}\end{aligned}}}$

Cette définition étend celle des produits intérieur et extérieur définis plus haut pour les vecteurs, c'est-à-dire pour r = s = 1.

Hestenes, Li et Rockwood 2001 proposent aussi une définition récursive, équivalente.

La donnée d'une lame non dégénérée A_r permet d'écrire tout vecteur a selon une décomposition dite orthogonale :

${\displaystyle \mathbf {a} =P_{A_{r}}(\mathbf {a} )+P_{A_{r}}^{\perp }(\mathbf {a} )\quad {\rm {avec}}\quad P_{A_{r}}(\mathbf {a} )=(\mathbf {a} \cdot A_{r})A_{r}^{-1}\quad {\rm {et}}\quad P_{A_{r}}^{\perp }(\mathbf {a} )=(\mathbf {a} \wedge A_{r})A_{r}^{-1}.}$

${\displaystyle P_{A_{r}}(\mathbf {a} )}$ et ${\displaystyle P_{A_{r}}^{\perp }(\mathbf {a} )}$ sont appelés respectivement projection et réjection.

Les éléments de ${\displaystyle {\mathcal {G}}}$ sont appelés multivecteurs. Hestenes utilise aussi parfois l'expression directed number, qu'on peut traduire par nombre orienté. Cependant, le terme multivecteur semble prévaloir dans les publications récentes.

Un verseur (versor en anglais) est un multivecteur qui peut être écrit comme produit géométrique de vecteurs non « nuls ».

Le commutateur de deux multivecteurs ${\displaystyle A,B\in {\mathcal {G}}}$ est défini comme la moitié[4] du commutateur usuel dans un anneau :

${\displaystyle A\times B={\frac {1}{2}}(AB-BA).}$

La réversion d'un multivecteur M est le multivecteur[10] :

${\displaystyle M^{\dagger }=\sum _{k\geq 0}(-1)^{\frac {k(k-1)}{2}}\langle M\rangle _{k}.}$

Certains auteurs utilisent le symbole tilde au lieu de l'obèle.

L'opérateur ${\displaystyle M\mapsto M^{\dagger }}$ est appelé antiautomorphisme principal de ${\displaystyle {\mathcal {G}}}$. C'est un antiautomorphisme d'algèbre, puisque

${\displaystyle (\mathbf {a} _{1}\mathbf {\ldots } \mathbf {a} _{k})^{\dagger }=\mathbf {a} _{k}\mathbf {\ldots } \mathbf {a} _{1}.}$

L'involution par grade, ou conjugaison paritaire ou conjugaison d'un multivecteur M est le multivecteur[10] :

${\displaystyle M^{*}=\sum _{k\geq 0}(-1)^{k}\langle M\rangle _{k}.}$

L'opérateur ${\displaystyle M\mapsto M^{*}}$ est une involution appelée involution principale de ${\displaystyle {\mathcal {G}}}$.

Un multivecteur est dit pair lorsque M^* = M. Il est dit impair lorsque M^* = –M.

La grandeur d'un multivecteur M est le scalaire positif[10] :

${\displaystyle |M|={\sqrt {\sum _{k}|\langle M\rangle _{k}\cdot \langle M\rangle _{k}|}}}$

Dans le cas particulier d'un k-vecteur, on a donc :

${\displaystyle |A_{k}|={\sqrt {|\langle A_{k}^{2}\rangle |}},}$

ce qui étend la définition donnée plus haut pour k = 1.

La grandeur constitue une norme de l'algèbre géométrique. Le terme norme est donc aussi utilisé.

Le produit scalaire de deux multivecteurs M et N est la partie scalaire du produit géométrique de M par la réversion de N[10] :

${\displaystyle \langle MN^{\dagger }\rangle =\langle NM^{\dagger }\rangle .}$

(Le produit scalaire de deux vecteurs est donc égal à leur produit intérieur : ${\displaystyle \langle \mathbf {a} \mathbf {b} ^{\dagger }\rangle =\mathbf {a} \cdot \mathbf {b} }$)

Une base canonique est une base de ${\displaystyle {\mathcal {G}}}$ (vu en tant qu'espace vectoriel) telle qu'il existe une base orthonormée ${\displaystyle (\mathbf {e} _{1},\mathbf {e} _{2},...)}$ dans laquelle les éléments de la base canonique peuvent s'écrire[11] :

${\displaystyle e_{J}=\mathbf {e} _{\sigma _{1}}\mathbf {e} _{\sigma _{2}}\ldots \mathbf {e} _{\sigma _{k}}}$

où ${\displaystyle J=(\sigma _{1},\sigma _{2}\ldots \sigma _{k})}$ est une suite finie et strictement croissante d'entiers positifs.

Les définitions de cette sous-section ne sont valables que lorsque ${\displaystyle {\mathcal {V}}}$ est de dimension finie n.

Un pseudoscalaire est une lame dont le grade n est égal à la dimension de l'espace. Tous les pseudoscalaires sont multiples les uns des autres, c'est-à-dire que ${\displaystyle \mathrm {dim} {\mathcal {G}}_{n}=\mathrm {dim} {\mathcal {G}}_{0}=1}$

Tous les pseudoscalaires unitaires[12], notés ${\displaystyle I_{\sigma }}$, sont égaux à un signe moins près. Cette quasi-unicité justifie une notation indépendante du choix des vecteurs ${\displaystyle \mathbf {\sigma } }$, ainsi que l'utilisation de l'article défini.

Le pseudoscalaire unitaire est donc défini par :

${\displaystyle I=\pm I_{\sigma }}$

La grandeur d'un pseudoscalaire par rapport au pseudoscalaire unitaire est notée avec des crochets encadrant et est définie comme le produit du pseudoscalaire considéré par l'inverse du pseudoscalaire unitaire :

${\displaystyle [P]=PI^{-1}}$

Le dual d'un multivecteur M est :

${\displaystyle {\widetilde {M}}=M^{\sim }=MI^{-1}.}$

Tout comme le pseudoscalaire unitaire, le dual n'est donc défini qu'au signe près.

L'intersection (meet en anglais) de deux multivecteurs est[10] :

${\displaystyle M\vee N={\widetilde {M}}\cdot N.}$

De façon générale, les transformations linéaires sur ${\displaystyle {\mathcal {V}}}$ sont notées avec un symbole souligné ou surligné.

Il est important de garder à l'esprit qu'une transformation linéaire n'est pas un élément de l'algèbre géométrique. Une expression telle que ${\displaystyle {\underline {f}}\mathbf {a} }$ ne désigne donc pas un produit géométrique mais bien l'application de la fonction linéaire ${\displaystyle {\underline {f}}}$ sur a.

Pour tout endomorphisme ${\displaystyle {\underline {f}}}$ de ${\displaystyle {\mathcal {V}}}$, il existe un unique endomorphisme ${\displaystyle {\overline {f}}}$ de ${\displaystyle {\mathcal {V}}}$ tel que :

${\displaystyle \forall (\mathbf {a} ,\mathbf {b} )\in {\mathcal {V}}^{2},\quad \mathbf {a} \cdot {\underline {f}}\mathbf {b} =\mathbf {b} \cdot {\overline {f}}\mathbf {a} .}$

${\displaystyle {\overline {f}}}$ est alors appelé endomorphisme adjoint de ${\displaystyle {\underline {f}}}$.

Tout endomorphisme ${\displaystyle {\underline {f}}}$ sur ${\displaystyle {\mathcal {V}}}$ peut être naturellement étendu sur ${\displaystyle {\mathcal {G}}}$[10] :

${\displaystyle {\underline {f}}(A\wedge B)={\underline {f}}(A)\wedge {\underline {f}}(B)}$

Cette extension est appelé ectomorphisme[13], compte tenu du fait qu'elle préserve le produit extérieur.

De la même façon pour toute lame ${\displaystyle A_{k}=\bigwedge _{j=1}^{k}\mathbf {a} _{j}}$ :

${\displaystyle {\underline {f}}(A_{k})=\bigwedge _{j=1}^{k}{\underline {f}}(\mathbf {a} _{j})}$

La linéarité permet alors d'étendre ${\displaystyle {\underline {f}}}$ à tout ${\displaystyle {\mathcal {G}}}$.

La notion d'endomorphisme adjoint peut être généralisée aux ectomorphismes par la relation :

${\displaystyle \langle A{\underline {f}}B\rangle =\langle B{\overline {f}}A\rangle }$

Une transformation linéaire U est dite orthogonale lorsqu'elle préserve le produit intérieur :

${\displaystyle \forall (\mathbf {a} ,\mathbf {b} )\in ({\mathcal {V}})^{2},\quad ({\underline {U}}\mathbf {a} )\cdot ({\underline {U}}\mathbf {b} )=\mathbf {a} \cdot \mathbf {b} .}$

Cette définition est équivalente à la caractérisation suivante :

${\displaystyle {\underline {U}}^{-1}={\overline {U}}.}$

Une transformation linéaire U est orthogonale si et seulement si il existe un verseur U tel que :

${\displaystyle \forall \mathbf {a} \in {\mathcal {V}},\quad {\underline {U}}\mathbf {a} =U\mathbf {a} (U^{*})^{-1}=U^{*}\mathbf {a} U^{-1}.}$

Il s'agit de la forme dite canonique d'une transformation orthogonale.

Tout comme la donnée d'un espace vectoriel permet l'analyse vectorielle, c'est-à-dire l'étude du calcul infinitésimal pour des fonctions définies sur cet espace vectoriel à valeurs scalaires ou vectorielles, la donnée d'une algèbre géométrique, dont les éléments sont appelés multivecteurs, permet l'analyse dite multivectorielle des fonctions définies sur ${\displaystyle {\mathcal {V}}}$ mais à valeurs cette fois potentiellement multivectorielles. Les anglo-saxons, à l'instar d'Hestenes, parlent de geometric calculus ou multivector calculus, tout comme ils parlent de vector calculus pour désigner ce que les francophones appellent analyse vectorielle.

L'outil le plus important pour cette discipline est probablement l'opérateur dit de dérivation vectorielle, qu'on peut définir ainsi :

${\displaystyle {\begin{array}{rccl}\partial$ :&{\mathcal {G}}^{\mathcal {V}}&\rightarrow &{\mathcal {G}}^{\mathcal {V}}\\&F&\mapsto &\left(\mathbf {x} \mapsto \sum _{j}\mathbf {e} ^{j}\lim _{\epsilon \rightarrow 0}{\frac {F(\mathbf {x} +\epsilon \mathbf {e} _{j})-F(\mathbf {x} )}{\epsilon }}\right)\end{array}}}

Cette définition est le plus souvent notée ∂ = e^j ∂_j, en utilisant la convention de sommation d'Einstein. Le symbole ∇ est aussi très souvent utilisé.

${\displaystyle \nabla =\mathbf {e} ^{j}\partial _{j}}$

On montre (cf. « Analyse géométrique ») que cette définition a un sens dans la mesure où l'expression e^j ∂_j forme un opérateur qui ne dépend pas de la base choisie.

Certains auteurs appellent cet opérateur gradient.

Les produits intérieur et extérieur de deux vecteurs sont, par construction, respectivement symétrique et antisymétrique :

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=\mathbf {b} \cdot \mathbf {a} \\\mathbf {a} \wedge \mathbf {b} &=-\mathbf {b} \wedge \mathbf {a} \end{aligned}}}$

Plus généralement, le produit extérieur de plusieurs vecteurs est antisymétrique :

${\displaystyle \forall \sigma \in {\mathfrak {S}}_{k},\quad \bigwedge _{j=1}^{k}\mathbf {a} _{j}=\operatorname {sgn} (\sigma )\bigwedge _{j=1}^{k}\mathbf {a} _{\sigma (j)}}$

Cette observation, ajoutée à la définition de l'orthogonalité, permet de déduire les deux propriétés fondamentales suivantes :

Caractérisation algébrique de l'orthogonalité et de la colinéarité — 

• Deux vecteurs sont orthogonaux si et seulement si ils anti-commutent.
• Deux vecteurs sont colinéaires si et seulement si ils commutent.

C'est-à-dire[14] :

${\displaystyle {\begin{array}{ccccc}\mathbf {a} \perp \mathbf {b} &\iff &\mathbf {a} \cdot \mathbf {b} =0&\iff &\mathbf {a} \mathbf {b} =-\mathbf {b} \mathbf {a} \\\mathbf {a} \propto \mathbf {b} &\iff &\mathbf {a} \wedge \mathbf {b} =0&\iff &\mathbf {a} \mathbf {b} =\mathbf {b} \mathbf {a} \end{array}}}$

Une généralisation de la caractérisation algébrique de la colinéarité existe pour l'indépendance linéaire. En effet, ${\displaystyle k}$ vecteurs ${\displaystyle (\mathbf {a} _{1},\mathbf {a} _{2}\ldots ,\mathbf {a} _{k})}$ sont linéairement indépendants si et seulement si leur produit extérieur est non nul. Ou, de façon équivalente, ils sont linéairement dépendants si et seulement si leur produit extérieur est nul :

${\displaystyle \left(\exists (\alpha _{1},\alpha _{2}\ldots ,\alpha _{k})\in \mathbb {K} ^{k}\setminus \{(0,\ldots ,0)\}\quad \sum _{j}\alpha _{j}\mathbf {a} _{j}=0\right)\iff \bigwedge _{j=1}^{k}\mathbf {a} _{j}=0.}$

Pour tout sous-espace vectoriel ${\displaystyle {\mathcal {F}}}$ de ${\displaystyle {\mathcal {V}}}$ de dimension ${\displaystyle r}$, il existe une lame A_r telle que :

${\displaystyle \forall \mathbf {x} \in {\mathcal {V}}\quad {\bigl (}\mathbf {x} \in {\mathcal {F}}\iff \mathbf {x} \wedge A_{r}=0{\bigr )}.}$

Toute lame A_r caractérise donc un sous-espace vectoriel qui est alors dit sous-tendu, engendré ou dirigé par A_r.

Dans le cas particulier où ${\displaystyle {\mathcal {V}}}$ est de dimension finie, il vient : ${\displaystyle \forall \mathbf {x} \in {\mathcal {V}}\quad \mathbf {x} \wedge I=0.}$

Puisque le produit intérieur de deux vecteurs est un scalaire et qu'il est distributif et symétrique, il constitue une forme quadratique sur ${\displaystyle {\mathcal {V}}}$ et confère ainsi aux vecteurs de l'algèbre géométrique une structure quadratique naturelle.

Dans le cas défini précédemment comme euclidien, le produit intérieur est en outre défini positif, et satisfait donc aux conditions nécessaires et suffisantes pour définir un produit scalaire, rendant ainsi la structure quadratique euclidienne, d'où l'appellation « cas euclidien ». Dans ce cas, les notions de norme et d'orthogonalité définies précédemment coïncident respectivement avec les notions de norme euclidienne et d'orthogonalité au sens euclidien.

Le produit extérieur fournit (en oubliant le produit géométrique dont il est issu) une définition alternative de l'algèbre extérieure de ${\displaystyle {\mathcal {V}}}$[15] :

${\displaystyle \wedge {\mathcal {V}}={\mathcal {G}}\quad {\rm {car}}\quad {\mathcal {G}}=\bigoplus _{k}{\mathcal {G}}^{k}\quad {\rm {et}}\quad {\mathcal {G}}^{k}=\wedge ^{k}{\mathcal {V}}.}$

Le vocabulaire de l'algèbre géométrique recoupe donc celui des algèbres extérieures. Par exemple, une lame de grade ${\displaystyle k}$ est aussi appelée multivecteur de grade k, k-multivecteur ou encore k-vecteur.

Le carré de tout bivecteur unitaire (e₁e₂) construit à partir de deux vecteurs de signatures identiques, est égal à –1 :

${\displaystyle \mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=1\Rightarrow (\mathbf {e} _{1}\mathbf {e} _{2})^{2}=-1.}$

Dès lors, la sous-algèbre engendrée par le couple (1, e₁e₂) est un corps isomorphe au corps des complexes. Cet isomorphisme justifie alors la notation :

${\displaystyle i=\mathbf {e} _{1}\mathbf {e} _{2}}$

de telle sorte qu'on a :

${\displaystyle i^{2}=-1.}$

Ce résultat peut en fait être généralisé à toutes les lames unitaires dont le carré est égal à -1. Elles génèrent chacune avec la lame unitaire de grade nul un corps isomorphe au corps des complexes. C'est par exemple le cas pour le pseudoscalaire unitaire dans le cas euclidien de dimension 3 :

${\displaystyle I^{2}=-1.}$

Une lame unitaire de grade 1, c'est-à-dire un vecteur unitaire, peut aussi engendrer un corps isomorphe au corps des complexes. Il faut et suffit pour cela que sa signature soit négative. C'est notamment le cas lorsque la structure quadratique n'est pas euclidienne, mais Lorentzienne. Par ailleurs, lorsqu'il existe au moins deux vecteurs de signatures différentes, il est possible de construire un bivecteur unitaire j tel que j² = +1, et la sous-algèbre qu'il engendre avec l'unité est alors isomorphe au corps des nombres complexes déployés, donnant au sous-espace correspondant une structure géométrique hyperbolique.

Dans le cas particulier où n = 3, on peut former trois bivecteurs unitaires : ${\displaystyle i=\mathbf {e} _{1}\mathbf {e} _{2},\quad j=\mathbf {e} _{2}\mathbf {e} _{3}\quad {\rm {et}}\quad k=\mathbf {e} _{1}\mathbf {e} _{3}.}$

Dans le cas euclidien, on a de plus :

${\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1,}$

si bien que la sous-algèbre engendrée par (1, i, j, k) est isomorphe au corps des quaternions.

i, j et k ne sont pas exactement les bivecteurs unitaires naturellement générés par la base orthonormale. En effet, on a bien i = e₁ e₂, j = e₂ e₃, mais par contre k = –e₃ e₁. Dans sa thèse de doctorat[16], Richard Wareham mentionne cette différence et y voit la cause de certaines erreurs de signe apparaissant parfois avec l'utilisation des quaternions. Ce sujet est aussi abordé par Chris Doran[17].

${\displaystyle {\mathcal {G}}^{2}}$ est stable par commutateurs. À ce titre, et compte tenu de l'identité de Jacobi, il forme une algèbre de Lie.

Une algèbre géométrique hérite de sa structure d'anneau unitaire la notion d'inverse : un élément A est dit inversible s'il existe un élément A⁻¹ (qui est alors unique) tel que

${\displaystyle AA^{-1}=A^{-1}A=1.}$

Tout vecteur non « nul » de ${\displaystyle {\mathcal {V}}}$ est inversible :

${\displaystyle \mathbf {a} ^{-1}={\frac {\mathbf {a} }{\mathbf {a} ^{2}}}.}$

Les verseurs sont par conséquent inversibles, comme produits d'inversibles :

${\displaystyle A^{-1}={\frac {A^{\dagger }}{A^{\dagger }A}}.}$

Les identités remarquables suivantes sont mentionnées dans McDonald 2015. Toutes ne sont pas relevées du fait de notations légèrement différentes.

${\displaystyle {\begin{aligned}A\cdot (B\cdot C)&=(A\wedge B)\cdot C\\(\mathbf {a} \wedge \mathbf {b} )\cdot (\mathbf {c} \wedge \mathbf {d} )&=(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )-(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )\\\mathbf {a} \cdot (\mathbf {bc} )&=(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} -(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} \\\mathbf {a} \cdot (\mathbf {b} \wedge \mathbf {c} )&=(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} -\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )\end{aligned}}}$

Le produit extérieur a ∧ b n'est ni un scalaire, ni un vecteur : c'est un bivecteur, qui sera identifié plus tard comme le dual du vecteur issu du produit vectoriel. La différence entre les deux opérations étant que le bivecteur fourni par le produit extérieur est intrinsèque au plan des deux vecteurs, tandis que le produit vectoriel est noté comme un pseudovecteur perpendiculaire à ce plan.

Le produit extérieur de deux vecteurs peut être vu comme une aire orientée.

Un bivecteur unitaire s est le produit géométrique de deux vecteurs orthonormés que l'on peut, sans perdre en généralité, considérer comme les deux premiers vecteurs d'une base orthonormée (e₁, e₂, ...) :

${\displaystyle s=\mathbf {e} _{1}\mathbf {e} _{2}}$

L'orthonormalité de e₁ et e₂ donne, entre autres :

${\displaystyle s=\mathbf {e} _{1}\mathbf {e} _{2}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}=-\mathbf {e} _{2}\wedge \mathbf {e} _{1}=-\mathbf {e} _{2}\mathbf {e} _{1}}$

Le caractère remarquable de s provient du fait que le produit géométrique par s laisse stable l'espace vectoriel généré par (e₁, e₂, ...), et défini donc une transformation linéaire (ou plus précisément deux transformations linéaires, selon que la multiplication a lieu à droite ou à gauche), permettant ainsi une interprétation géométrique directe :

Le point important ici étant que e2
1 et e2
2 sont scalaires du fait du critère de contraction.

Le carré de s est un scalaire, car

${\displaystyle s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}.}$

Il est négatif si e₁ et e₂ ont la même signature, et positif dans le cas contraire. Le comportement algébrique (et géométrique dans le plan (e₁, e₂, ...)) de s est radicalement différent dans les deux cas.

Lorsque e₁ et e₂ ont la même signature, on a soit ${\displaystyle \mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=+1}$ soit ${\displaystyle \mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=-1}$. Dans les deux cas le bivecteur e₁e₂ a les mêmes propriétés algébriques et géométriques, mais pour fixer les idées on choisira ici ${\displaystyle \mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=+1}$, c'est-à-dire le cas euclidien.

On a alors la propriété importante ${\displaystyle s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=-1}$, c'est-à-dire :

${\displaystyle s^{2}=-1.}$

s engendre alors avec l'unité une sous-algèbre isomorphe au corps des complexes, comme vu plus haut. Ceci suggère d'utiliser dorénavant la lettre i au lieu de s dans cette section.

On aura également les relations suivantes :

${\displaystyle {\begin{aligned}i\mathbf {e_{1}} &=-\mathbf {e_{2}} \\i\mathbf {e_{2}} &=\mathbf {e_{1}} \end{aligned}}}$

${\displaystyle {\begin{aligned}\mathbf {e_{1}} i&=\mathbf {e_{2}} \\\mathbf {e_{2}} i&=-\mathbf {e_{1}} \end{aligned}}}$

C'est-à-dire que la multiplication par i tourne toute combinaison linéaire de (e₁, e₂, ...) d'un quart de tour, dans un sens qui dépend du côté selon lequel est effectuée la multiplication (à gauche ou à droite). On peut s'assurer du fait que la rotation est d'un quart de tour par exemple en remarquant que 4 est le plus petit entier k tel que i^k = 1. Il s'avère que cette rotation d'un quart de tour génère un groupe de rotations, comme il est montré ci-après.

Le produit géométrique d'une paire de vecteurs unitaires ${\displaystyle \mathbf {a} ,\mathbf {b} \,(|\mathbf {a} |=|\mathbf {b} |=1)\,}$ est noté U et est appelé tourneur[18]:

${\displaystyle U=\mathbf {ab} }$

Le nom tourneur est justifié par le fait que ${\displaystyle U}$ transforme a et b l'un envers l'autre par rotation:

${\displaystyle \mathbf {b} =\mathbf {a} U,\quad \mathbf {a} =U\mathbf {b} }$

Lorsque a et b sont dans le plan (e₁, e₂, ...), on peut sans perdre en généralité choisir e₁ = a et trouver un angle θ tel que :

${\displaystyle \mathbf {b} =\cos(\theta )\mathbf {e} _{1}+\sin(\theta )\mathbf {e} _{2}}$

U s'écrit alors :

${\displaystyle U=\mathbf {ab} =\cos(\theta )\mathbf {e} _{1}\mathbf {e} _{1}+\sin(\theta )\mathbf {e} _{1}\mathbf {e} _{2}=\cos(\theta )+\sin(\theta )\mathbf {e} _{1}\mathbf {e} _{2}}$

et donc, par association des parties scalaires et bivectorielles de la décomposition canonique:

${\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=\cos(\theta )\\\mathbf {a} \wedge \mathbf {b} &=i\sin(\theta )\end{aligned}}}$

où i est le bivecteur unitaire :

${\displaystyle i=\mathbf {e} _{1}\mathbf {e} _{2}={\frac {\mathbf {a} \wedge \mathbf {b} }{\sin(\theta )}}={\frac {U-\cos(\theta )}{\sin(\theta )}}.}$

Il est alors possible d'écrire :

${\displaystyle U=U_{\theta }=\mathbf {ab} =\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} =\cos(\theta )+i\sin(\theta )=e^{i\theta },}$

c'est-à-dire[19] :

${\displaystyle U_{\theta }=e^{i\theta }.}$

Lorsqu'on multiplie (par exemple à gauche) ce tourneur par un vecteur x(ϕ) tel que :

${\displaystyle \mathbf {x} (\phi )=\cos(\phi )\mathbf {e} _{1}+\sin(\phi )\mathbf {e} _{2}}$

on obtient, par application des identités trigonométriques ainsi que des règles algébriques d'orthonormalité de e₁ et e₂ :

${\displaystyle {\begin{aligned}\mathbf {x} (\phi )U_{\theta }&=\mathbf {x} (\phi )e^{i\theta }\\&=(\cos(\phi )\mathbf {e} _{1}+\sin(\phi )\mathbf {e} _{2})(\cos(\theta )+i\sin(\theta ))\\&=\cos(\phi )\mathbf {e} _{1}\cos(\theta )+\sin(\phi )\mathbf {e} _{2}\cos(\theta )+\cos(\phi )\mathbf {e} _{1}i\sin(\theta )+\sin(\phi )\mathbf {e} _{2}i\sin(\theta )\\&=(\cos(\phi )\cos(\theta )-\sin(\phi )\sin(\theta ))\mathbf {e} _{1}+(\cos(\theta )\sin(\phi )+\cos(\phi )\sin(\theta ))\mathbf {e} _{2}\\&=\cos(\phi +\theta )\mathbf {e} _{1}+\sin(\phi +\theta )\mathbf {e} _{2}\\&=\mathbf {x} (\phi +\theta ).\end{aligned}}}$

Le vecteur x(ϕ) a donc bien « tourné » d'un angle θ. Un calcul similaire montrerait qu'une multiplication à droite fait tourner x(ϕ) d'un angle –θ.

En résumé :

${\displaystyle {\begin{aligned}\mathbf {x} (\phi )U_{\theta }&=\mathbf {x} (\phi +\theta )\\U_{\theta }\mathbf {x} (\phi )&=\mathbf {x} (\phi -\theta ).\end{aligned}}}$

Le produit géométrique de deux vecteurs unitaires représente donc bien une rotation.

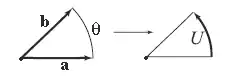
Il y a une analogie entre tourneur et vecteur.

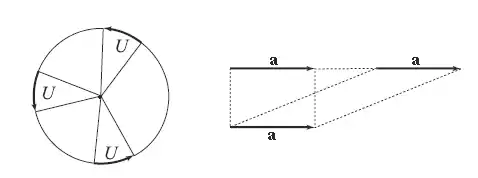
Une composition de rotation s'exprimera par le produit de deux tourneurs :

${\displaystyle U_{\theta }U_{\varphi }=U_{\theta +\varphi }}$

Il est utile d'observer que :

${\displaystyle U_{\varphi }\mathbf {x} (\phi )U_{\psi }=U_{\varphi }\mathbf {x} (\phi +\psi )=\mathbf {x} (\phi +\psi -\varphi )}$

et que donc, pour ϕ = –θ/2 et ψ = θ/2 :

${\displaystyle U_{-{\frac {\theta }{2}}}\mathbf {x} (\phi )U_{\frac {\theta }{2}}=\mathbf {x} (\phi +\theta )}$

Ceci constitue la formulation dite canonique de la rotation d'angle θ.

Lorsque e₁ et e₂ ont une signature différente (admettons par exemple, pour fixer les idées, que ${\displaystyle \mathbf {e} _{1}^{2}=1}$ et ${\displaystyle \mathbf {e} _{2}^{2}=-1}$), on a ${\displaystyle s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=1}$, c'est-à-dire :

${\displaystyle s^{2}=1}$

La multiplication par s intervertit e₁ et e₂ :

${\displaystyle \mathbf {e} _{1}s=\mathbf {e} _{1}\mathbf {e} _{1}\mathbf {e} _{2}=\mathbf {e} _{1}^{2}\mathbf {e} _{2}=\mathbf {e} _{2}}$

${\displaystyle \mathbf {e} _{2}s=\mathbf {e} _{2}\mathbf {e} _{1}\mathbf {e} _{2}=-\mathbf {e} _{2}\mathbf {e} _{2}\mathbf {e} _{1}=-\mathbf {e} _{2}^{2}\mathbf {e} _{1}=\mathbf {e} _{1},}$

c'est-à-dire :

${\displaystyle {\begin{aligned}\mathbf {e} _{1}s&=\mathbf {e} _{2}\\\mathbf {e} _{2}s&=\mathbf {e} _{1}\end{aligned}}}$

${\displaystyle {\begin{aligned}s\mathbf {e} _{1}&=-\mathbf {e} _{2}\\s\mathbf {e} _{2}&=-\mathbf {e} _{1}.\end{aligned}}}$

La multiplication par s agit donc dans le plan (e₁, e₂, ...) comme une réflexion dont l'axe est l'une des bissectrices des droites dirigées par e₁ et e₂, le choix de la bissectrice dépendant du côté où s'effectue la multiplication (à droite ou à gauche).

Le fait que s² = 1 est cohérent avec le caractère involutif des réflexions.

Sauf mention contraire, on se limitera à partir d'ici au cas euclidien.

On considère désormais un couple de vecteurs (a , b) non nécessairement unitaires, mais non nuls et non colinéaires. Les résultats précédents peuvent être généralisés en considérant le couple :

${\displaystyle (\mathbf {\tilde {a}} ,\mathbf {\tilde {b}} )=({\frac {\mathbf {a} }{|\mathbf {a} |}},{\frac {\mathbf {b} }{|\mathbf {b} |}})}$

Les vecteurs ${\displaystyle \mathbf {\tilde {a}} }$ et ${\displaystyle \mathbf {\tilde {b}} }$ sont, eux, unitaires, et ont les mêmes signatures que a et b. Ils sont aussi séparés par un même angle θ, de telle sorte que le tourneur ${\displaystyle \mathbf {\tilde {a}} \mathbf {\tilde {b}} }$ s'écrit :

${\displaystyle \mathbf {\tilde {a}} \mathbf {\tilde {b}} =e^{i\theta }}$

où

${\displaystyle i={\frac {\mathbf {\tilde {a}} \wedge \mathbf {\tilde {b}} }{\sin(\theta )}}.}$

Le produit géométrique peut donc s'écrire :

${\displaystyle \mathbf {a} \mathbf {b} =|\mathbf {a} ||\mathbf {b} |e^{i\theta }}$

tandis que le bivecteur unitaire i peut s'écrire :

${\displaystyle i={\frac {\mathbf {a} \wedge \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |\sin(\theta )}}.}$

On a vu précédemment que l'ensemble de multivecteurs engendré — par les combinaisons linéaires et produits géométriques — par 1 et i est un corps isomorphe au corps des nombres complexes. Ceci justifie l'emploi d'un vocabulaire et de notations analogues.

Ainsi, si l'on note z le produit ab, le scalaire

${\displaystyle |z|=|\mathbf {a} \mathbf {b} |=|\mathbf {a} ||\mathbf {b} |}$

est ce qu'on appelle le module de z. Il s'agit d'une notion très différente de la norme (ou grandeur) évoquée plus haut, car cette dernière n'est définie que pour les vecteurs, et z n'est pas un vecteur.

Tout comme un nombre complexe peut être décomposé en une partie réelle et une partie imaginaire, un produit géométrique peut être décomposé en deux parties qui ne sont ni plus ni moins que les produits intérieur et extérieur, qu'on peut aussi appeler symétrique et antisymétrique, ou encore scalaire et bivectoriel.

${\displaystyle {\begin{aligned}z&=\mathbf {a} \cdot \mathbf {b} &+&\mathbf {a} \wedge \mathbf {b} \\&=|z|\cos(\theta )&+&|z|i\sin(\theta ).\end{aligned}}}$

De la même façon, θ peut être appelé argument de z.

z peut être interprété géométriquement comme l'arc orienté d'un cercle de rayon z.

Le conjugué de z est le multivecteur de même partie scalaire mais de composante bivectorielle opposée :

${\displaystyle z^{\dagger }=(\mathbf {ab} )^{\dagger }=\mathbf {a} \cdot \mathbf {b} -\mathbf {a} \wedge \mathbf {b} =\mathbf {b} \cdot \mathbf {a} +\mathbf {b} \wedge \mathbf {a} =\mathbf {ba} }$

Le conjugué d'un produit géométrique apparaît donc comme le produit géométrique effectué en ordre inverse :

${\displaystyle (\mathbf {ab} )^{\dagger }=\mathbf {ba} .}$

Ce fait peut être utilisé pour calculer le module du produit géométrique z.

${\displaystyle |zz^{\dagger }|=|\mathbf {a} \mathbf {b} \mathbf {b} \mathbf {a} |=|\mathbf {a} ^{2}\mathbf {b} ^{2}|=|\mathbf {a} |^{2}|\mathbf {b} |^{2}=|z|^{2}}$

autrement dit :

${\displaystyle |z|={\sqrt {|zz^{\dagger }|}}.}$

Les produits géométriques peuvent être utilisés directement sur les vecteurs :

${\displaystyle \mathbf {b} =\mathbf {a} ^{-1}z=z^{\dagger }\mathbf {a} ^{-1}}$

avec l'inverse du vecteur a donné par

${\displaystyle \mathbf {a} ^{-1}={\frac {1}{\mathbf {a} }}={\frac {\mathbf {a} }{\mathbf {a} ^{2}}}={\frac {\mathbf {a} }{|\mathbf {a} |^{2}}}.}$

Ici, le produit géométrique z opère une rotation sur le vecteur a, le met à l'échelle pour donner le vecteur b (c'est une similitude).

Soit l'espace vectoriel euclidien ${\displaystyle {\mathcal {P}}^{3}}$. Par multiplication et addition, les vecteurs engendrent une algèbre géométrique ${\displaystyle {\mathcal {G}}_{3}={\mathcal {G}}\left({\mathcal {P}}^{3}\right)}$. En particulier, on peut construire une base pour l'algèbre géométrique à partir de la base orthonormée canonique ${\displaystyle \lbrace \mathbf {\sigma _{1}} ,\mathbf {\sigma _{2}} ,\mathbf {\sigma _{3}} \rbrace }$ de ${\displaystyle {\mathcal {P}}^{3}}$.

À l'aide du produit géométrique, on peut définir l'unité pseudoscalaire (qui représente un volume orienté) :

${\displaystyle i=\mathbf {\sigma _{1}} \mathbf {\sigma _{2}} \mathbf {\sigma _{3}} .}$

On a également la base de bivecteurs suivante

${\displaystyle \mathbf {\sigma _{1}} \mathbf {\sigma _{2}} =i\mathbf {\sigma _{3}} ,\,\mathbf {\sigma _{2}} \mathbf {\sigma _{3}} =i\mathbf {\sigma _{1}} ,\,\mathbf {\sigma _{3}} \mathbf {\sigma _{1}} =i\mathbf {\sigma _{2}} }$

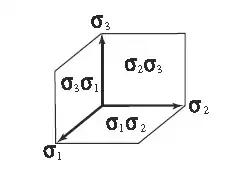
Les bivecteurs unités représentent des aires orientées.

Le pseudoscalaire i a des propriétés spéciales qui facilitent le passage entre l'espace vectoriel euclidien et l'algèbre géométrique. On a :

${\displaystyle i^{2}=-1}$

Tout bivecteur B de ${\displaystyle {\mathcal {G}}_{3}}$ est le dual d'un vecteur b en considérant la relation :

${\displaystyle \mathbf {B} =i\mathbf {b} =\mathbf {b} i}$

Ainsi l'opération de dualité géométrique est simplement exprimée par la multiplication par le pseudoscalaire i. Cela permet d'écrire le produit extérieur sous cette forme :

${\displaystyle \mathbf {a} \wedge \mathbf {b} =i\mathbf {a} \times \mathbf {b} }$,

a × b étant le « cross-product anglo-saxon », qui correspond au produit vectoriel dans la littérature scientifique française, lequel produit vectoriel est malencontreusement noté ∧ comme le produit extérieur. Le produit vectoriel est ainsi implicitement défini comme le dual du produit extérieur. Par conséquent, la décomposition canonique du produit géométrique peut être mise sous la forme :

${\displaystyle \mathbf {a} \mathbf {b} =\mathbf {a} \cdot \mathbf {b} +i\mathbf {a} \times \mathbf {b} }$

C'est grâce à cette définition que l'on pourra faire le lien entre l'algèbre géométrique et l'analyse vectorielle standard.

Les éléments d'une algèbre géométrique sont dénommés des multivecteurs. Les propriétés spéciales du pseudoscalaire i permettent d'écrire tout multivecteur M de ${\displaystyle {\mathcal {G}}_{3}}$ dans sa forme étendue :

${\displaystyle M=\alpha +\mathbf {a} +i\mathbf {b} +i\beta }$,

où α et β sont des scalaires et où a et b sont des vecteurs. L'intérêt de cette formulation est qu'elle réduit la multiplication de multivecteurs dans ${\displaystyle {\mathcal {G}}_{3}}$ à celle des vecteurs. Les quatre termes d'un multivecteur sont linéairement indépendant, ainsi les parties scalaire, vecteur, bivecteur et pseudoscalaire des multivecteurs se combinent séparément lors d'une addition, ce qui n'est pas le cas pour la multiplication.

L'algèbre géométrique ${\displaystyle {\mathcal {G}}_{3}}$ est un espace linéaire de dimension 1+3+3+1=2³=8.

La forme étendue d'un multivecteur a la structure algébrique formelle d'un « scalaire complexe » α + i β augmenté d'un « vecteur complexe » a + i b, mais toute interprétation physique repose sur la signification géométrique du pseudoscalaire i.

Avec les quaternions

Algèbre géométrique	Quaternions	Interprétation
1	1	scalaire
${\displaystyle \sigma _{2}\sigma _{3}}$	-i	plan orienté yz
${\displaystyle \sigma _{3}\sigma _{1}}$	-j	plan orienté zx
${\displaystyle \sigma _{1}\sigma _{2}}$	-k	plan orienté xy

Avec les biquaternions

Algèbre géométrique	Biquaternions	Interprétation
1	1	point défini par son rayon-vecteur
${\displaystyle \sigma _{1}}$	i i	droite orientée (vecteur selon l'axe x)
${\displaystyle \sigma _{2}}$	i j	droite orientée (vecteur selon l'axe y)
${\displaystyle \sigma _{3}}$	i k	droite orientée (vecteur selon l'axe z)
${\displaystyle \sigma _{1}\sigma _{2}}$	-k	plan orienté xy (bivecteur)
${\displaystyle \sigma _{2}\sigma _{3}}$	-i	plan orienté yz (bivecteur)
${\displaystyle \sigma _{3}\sigma _{1}}$	-j	plan orienté zx (bivecteur)
${\displaystyle \sigma _{1}\sigma _{2}\sigma _{3}}$	i	volume orienté xyz (trivecteur)

Avec l'algèbre des matrices

L'algèbre géométrique ${\displaystyle {\mathcal {G}}_{3}}$ est analogue à l'algèbre construite sur des matrices 2 × 2 à coefficients complexes. Cette algèbre se retrouve en mécanique quantique, introduite par Wolfgang Pauli, pour modéliser le spin des particules. La base canonique de cette algèbre est constituée des huit matrices complexes de dimensions 2 × 2 suivantes :

• pour les vecteurs, les trois matrices de Pauli :

${\displaystyle \sigma _{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}},\quad \sigma _{2}=\sigma _{y}={\begin{pmatrix}0&-i\\i&0\end{pmatrix}},\quad \sigma _{3}=\sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}~;}$

• pour les bivecteurs :

${\displaystyle \sigma _{1}\sigma _{2}=\sigma _{xy}={\begin{pmatrix}i&0\\0&-i\end{pmatrix}},\quad \sigma _{2}\sigma _{3}=\sigma _{yz}={\begin{pmatrix}0&i\\i&0\end{pmatrix}},\quad \sigma _{3}\sigma _{1}=\sigma _{zx}={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}~;}$

• pour les trivecteurs :

${\displaystyle \sigma _{1}\sigma _{2}\sigma _{3}=\sigma _{xyz}={\begin{pmatrix}i&0\\0&i\end{pmatrix}}~;}$

• pour les scalaires :

${\displaystyle \sigma _{0}=1={\begin{pmatrix}1&0\\0&1\end{pmatrix}}.}$