On va prouver dans ce chapitre que tous les groupes simples d'ordre 168 sont isomorphes entre eux et donc, puisque, d'après le chapitre sur la simplicité des groupes linéaires spéciaux projectifs, PSL(2, 7) est un groupe simple d'ordre 168, isomorphes à PSL(2, 7). Cela n'est pas une matière classique et ne servira pas dans la suite du cours, donc le lecteur non intéressé peut omettre ce chapitre.
Section 1. Préliminaires de théorie des groupes
Notation. Pour tout groupe fini G et tout nombre premier p, on notera l'ensemble des p-sous-groupes de Sylow de G et on notera le cardinal de , autrement dit le nombre des p-sous-groupes de Sylow de G.
Soit G un groupe simple d'ordre au moins 3. On suppose que G a un sous-groupe propre d'indice fini k. Alors G est isomorphe à un sous-groupe du groupe alterné . En particulier, divise k!/2.
Soit G un groupe fini, soit p un nombre premier. Écrivons avec m non divisible par p. Supposons que pour tout couple (P, Q) de différents p-sous-groupes de Sylow de G, Alors
On l'a démontré dans un exercice de la série Théorèmes de Sylow (forme forte du théorème de congruence de Sylow).
La dénomination « lemme de l'intersection maximale » qu'on donne ici à l'énoncé qui suit n'est pas standard.
Soit G un groupe fini, soit p un diviseur premier de l'ordre de G. Désignons par (intersections deux à deux des p-sous-groupes de Sylow de G) l'ensemble des où (P, Q) parcourt les couples de p-sous-groupes de Sylow de G tels que Soient P et Q deux différents p-sous-groupes de Sylow de G tels que soit maximal dans ordonné par inclusion. Posons Alors et sont deux différents p-sous-groupes de Sylow de N et ils contiennent strictement.
Prouvons d'abord que
- (thèse 1) et contiennent strictement.
Puisque P est un p-groupe et donc un groupe nilpotent; puisque, d'autre part, est clairement un sous-groupe propre de P (l'intersection de deux différents ensembles finis de même cardinal est strictement contenue dans chacun de ces deux ensembles), il résulte d'une proposition du chapitre Groupes nilpotents que
Le second membre est égal à donc
De même,
Nous avons donc prouvé notre thèse (1), à savoir que
- (2) et contiennent strictement.
Prouvons maintenant que
- (thèse 3) et sont des p-sous-groupes de Sylow de N.
Puisque et sont des p-sous-groupes de N,
il existe un p-sous-groupe de Sylow de N qui contient
et il existe un p-sous-groupe de Sylow de N qui contient
De même,
il existe un p-sous-groupe de Sylow de G qui contient
et il existe un p-sous-groupe de Sylow de G qui contient .
Comme et contiennent tous deux
- (4) contient
On a vu en (2) que contient strictement, donc d'après (4)
- contient strictement.
Puisque et sont des p-sous-groupes de Sylow de G, il résulte donc de la maximalité de dans que
- (5)
De même,
- (6)
Puisque (par hypothèse sur ) est contenu dans , (5) donne d'où (puisque est supposé contenu dans N)
Par hypothèse sur nous avons aussi l'inclusion réciproque, donc
donc, vu les hypothèses sur
- est un p-sous-groupe de Sylow de N.
De même, est un p-sous-groupe de Sylow de N.
Nous avons donc prouvé notre thèse (3), à savoir que
- (7) et sont des p-sous-groupes de Sylow de N.
Prouvons que et sont distincts.
Nous avons
d'où (vu la définition de N)
Donc si et étaient égaux, on aurait ce qui contredit (2). Nous avons donc prouvé que et sont distincts, ce qui, joint à (2) et à (7), démontre l'énoncé.
Soit G un groupe fini, soit p un nombre premier, soit P un p-sous-groupe de Sylow de G, soient U et W des sous-groupes normaux de P. Pour que U et W soient conjugués dans G, il faut et il suffit qu'ils soient conjugués dans
Soit G un groupe fini dont l'ordre divise 24. Ou bien G a un 2-sous-groupe de Sylow normal, ou bien G a un 3-sous-groupe de Sylow normal ou bien G est isomorphe au groupe symétrique .
On peut supposer que et sont distincts de 1; il s'agit alors de prouver que G est isomorphe au groupe symétrique
D'après les théorèmes de Sylow, et Toujours d'après les théorèmes de Sylow, il en résulte que l'ordre de G est divisible par 4 (et par 3, et donc par 12). De résulte qu'il y a exactement 8 éléments d'ordre 3 dans G (car les 3-sous-groupes de Sylow de G sont d'ordre premier et se coupent donc trivialement deux à deux). On a vu que l'ordre de G est divisible par 4, donc l'ordre des 2-sous-groupes de Sylow de G est au moins égal à 4; de plus, donc il y a au moins 5 éléments de G dont les ordres sont des puissances de 2. Donc G comprend au moins 8 + 5 = 13 éléments. Puisque l'ordre de G est supposé diviser 24, on a donc
On a prouvé dans un exercice de la série Groupes alternés que tout groupe d'ordre 24 qui a plus d'un 2-sous-groupe de Sylow et plus d'un 3-sous-groupe de Sylow est isomorphe à donc l'énoncé est démontré.
Les 2-sous-groupes de Sylow de sont tous isomorphes au groupe diédral d'ordre 8.
On a vu au chapitre Groupes diédraux que pour tout nombre naturel n ≥ 3, le groupe symétrique contient un sous-groupe diédral d'ordre 2n. En faisant n = 4, on trouve que contient un sous-groupe diédral d'ordre 8, d'où l'énoncé, puisque les 2-sous-groupes de Sylow d'un même groupe sont isomorphes.
Le seul 2-sous-groupe normal non trivial de est le groupe de Klein
Cela résulte d'un exercice de la série Théorie des groupes/Exercices/Groupes alternés où on a déterminé tous les sous-groupes normaux de
Soit G un groupe simple fini, soit p un diviseur premier de l'ordre de G, soit P un p-sous-groupe de Sylow de G. On suppose que P est abélien et que est égal à , où q est un nombre premier. Alors est égal à P.
Puisque P est abélien, nous avons Puisque l'indice de P dans est égal à q, qui est un nombre premier, il en résulte (formule des indices) que est égal à P ou à Si était égal à alors, d'après le théorème du complément normal de Burnside, P aurait un complément normal N dans G. Mais les hypothèses entraînent évidemment 1 < P < G, d'où 1 < N < G, ce qui est impossible puisque G est supposé simple. Donc est égal à P.
L'ordre du groupe n'est pas divisible par 3.
Il résulte d'un exercice de la série Holomorphe d'un groupe que est isomorphe à Hol(Z/4Z). Or l'ordre de Hol(Z/4Z) est et n'est donc pas divisible par 3.
Le centre de est un sous-groupe d'ordre 2 de
Voir un exercice de la série Groupes diédraux, où on a déterminé le centre d'un groupe diédral quelconque.
Soit D un groupe diédral d'ordre 8. Alors D a exactement deux sous-groupes de Klein. Ces deux sous-groupes ne sont pas conjugués dans D. Ils engendrent D.
Un sous-groupe de Klein de D est d'indice 2 dans D et est donc normal dans D. Dès lors, le fait que D a exactement deux sous-groupes de Klein se déduit d'un exercice de la série Groupes diédraux où on a déterminé les sous-groupes normaux d'un groupe diédral. Puisque les deux sous-groupes de Klein de D sont normaux dans D, ils ne sont pas conjugués dans D. Le sous-groupe de D engendré par ces deux sous-groupes a pour ordre un multiple de 4 qui divise 8 et est strictement supérieur à 4. Cet ordre est donc égal à 8, donc les deux sous-groupes de Klein de D engendrent D.
(i) Deux sous-groupes de Klein non normaux de engendrent toujours
(ii) Le groupe a exactement trois 2-sous-groupes de Sylow. Chacun de ces sous-groupes contient exactement 2 groupes de Klein, à savoir l'unique sous-groupe de Klein normal de et un sous-groupe de Klein qui n'est pas conjugué de dans .
Démontrons le point (i). Soient V et W deux sous-groupes de Klein non normaux de . Il s'agit de prouver que V et W engendrent . Le sous-groupe H de engendré par V et W est d'ordre divisible par 4 et > 4, donc son ordre est égal à 8, à 12 ou à 24. Si l'ordre de H est égal à 8, H est un 2-sous-groupe de Sylow de et donc (préliminaire 6) un groupe diédral d'ordre 8. On sait que a un unique sous-groupe de Klein normal, soit (voir préliminaire 7). Puisque est un 2-sous-groupe normal de , il est contenu dans chaque 2-sous-groupe de Sylow de et en particulier dans H. Mais, d'après le préliminaire 11, un groupe diédral d'ordre 8 n'a que deux sous-groupes de Klein, donc V ou W est égal à V_{4} et est donc normal dans S_{4}, contradiction. Donc l'ordre de H est égal à 12 ou à 24. Le seul sous-groupe d'ordre 12 de est , qui n'a qu'un sous-groupe de Klein, donc H n'est pas d'ordre 12. Donc H est d'ordre 24 et est donc égal à , ce qui démontre le point (i).
Démontrons maintenant le point (ii). D'après les théorèmes de Sylow, le nombre des 2-sous-groupes de Sylow de divise 3. S'il était égal à 1, aurait un sous-groupe normal d'ordre 8, ce qui contredit le préliminaire 7. Donc a exactement trois 2-sous-groupes de Sylow. Soit D un de ces sous-groupes. Comme déjà noté, est contenu dans chaque 2-sous-groupe de Sylow de S_{4}, donc est contenu dans D. Comme rappelé dans la démonstration du point (i), D a exactement 2 sous-groupes de Klein. Celui qui est différent de ne peut pas être conjugué de dans , puisque est normal dans S_{4}. On a donc démontré le point (ii).
Section 2. Préliminaires de géométrie projective. Le plan de Fano.
Les structures d'incidence, leurs isomorphimes et leurs automorphismes.
Une structure d'incidence est un triple où et sont des ensembles et où est une partie de
On dit alors que les éléments de sont les points de cette structure, que les éléments de sont les lignes et que est la relation d'incidence. P étant un point et L une ligne, on dit que P est sur L si (P, L) appartient à Dans le même cas, on dit aussi que L passe par P. On dit que des points sont alignés s'il existe une ligne qui passe par tous ces points.
Si le triple est une structure d'incidence, alors le triple où désigne le graphe réciproque du graphe est lui aussi une structure d'incidence, qu'on appelle la structure d'incidence duale de
Si les triples et sont des structures d'incidence, un isomorphisme de sur est par définition un couple (f, g), où f est une bijection de sur où g est une bijection de sur et où, pour tout point P et toute ligne L de , (f(P), g(L)) appartient à si et seulement si (P, L) appartient à
On vérifie facilement que si , et sont des structures d'incidence, si est un isomorphisme de sur si est un isomorphisme de sur alors est un isomorphisme de sur On appelle cet isomorphisme le composé de et
Un isomorphisme d'une structure d'incidence sur elle-même est appelé un automorphisme de cette structure d'incidence. Le composé de deux automorphismes d'une structure d'incidence est par définition leur composé comme isomorphismes. C'est lui-même un automorphisme de L'ensemble des automorphismes de muni de la composition des automorphismes, est un groupe qu'on appelle le groupe des automorphismes de Si deux structures d'incidence sont isomorphes, le groupe des automorphismes de l'une est isomorphe au groupe des automorphismes de l'autre.
Supposons que soit une structure d'incidence où une ligne est caractérisée par les points qui sont sur cette ligne; on entend par là que si et sont des lignes telles que les points sur sont exactement les points sur alors et sont égales. Dans ce cas, un isomorphisme (f, g) d'une structure d'incidence sur est caractérisé par sa première composante f; on entend par là que si et sont des isomorphismes de sur alors ce qu'on peut encore exprimer en disant que dans l'automorphisme (f, g), g est déterminée par f. En effet, on montre facilement qu'alors, pour toute ligne L' de g(L') doit être l'unique ligne L de telle que les points sur L soient exactement les f(P'), où P' parcourt les points sur L'.
Dans la définition qui suit, on adopte l'expression « plan de type projectif », utilisée par Jacqueline Lelong-Ferrand pour distinguer cette notion de la notion plus étroite de plan projectif associé à un espace vectoriel[1].
Un plan de type projectif est une structure d'incidence satisfaisant aux conditions suivantes :
a) pour tous différents points P et Q, il y a une et une seule ligne qui passe par ces deux points;
b) pour toutes différentes lignes L et M, il y a un et un seul point qui est sur chacune de ces deux lignes;
c) il y a un ensemble de 4 points tel que pour toute partie {P, Q, R} à trois éléments de cet ensemble, P, Q et R ne soient pas alignés.
Un ensemble tel qu'en c), c'est-à-dire un ensemble de 4 points dont 3 ne sont jamais alignés, est appelé un quadrangle.
Si P et Q sont deux points distincts, l'unique ligne passant par P et par Q est aussi appelée la ligne joignant P et Q; on la notera PQ.
Si L et M sont deux lignes distinctes, l'unique point se trouvant sur L et sur M est appelé le point d'intersection de L et de M.
On vérifie facilement qu'une structure d'incidence isomorphe à un plan de type projectif est elle-même un plan de type projectif.
Nous définirons un plan de Fano comme un plan de type projectif ayant exactement 7 points et 7 lignes, où chaque point est exactement sur 3 lignes et où chaque ligne passe exactement par 3 points.
Remarque. On peut prouver que pour tout plan de type projectif fini (c'est-à-dire pour tout plan projectif n'ayant qu'un nombre fini de points et de lignes), il y a un nombre naturel tel que
- le nombre de points et le nombre de lignes sont égaux à
- chaque ligne passe exactement par q + 1 points,
- chaque point se trouve sur exactement q+1 lignes.
Ce nombre q est appelé l'ordre du plan de type projectif en question. Un plan de Fano peut donc être défini comme un plan de type projectif d'ordre 2. Nous ne nous servirons cependant pas de cette notion d'ordre.
Il est clair qu'une structure d'incidence isomorphe à un plan de Fano est elle-même un plan de Fano.
Puisque dans un plan de Fano, toute ligne passe par trois points et que, de même que dans tout plan de type projectif, toute ligne est déterminée par deux de ses points, toute ligne d'un plan de Fano est déterminée par les points qui sont sur cette ligne. D'après une remarque faite plus haut, il en résulte que dans un isomorphisme (f, g) de plans de Fano, la bijection g est déterminée par f. (Le théorème cité ci-dessus sur l'ordre d'un plan de type projectif permet de prouver la même chose pour tout plan de type projectif.)
Prenons pour l'ensemble {1, 2, 3, 4, 5, 6, 7} et pour l'ensemble ayant pour éléments les ensembles {1, 2, 3}, {1, 4, 5}, {1, 6, 7}, {2, 4, 6}, {2, 5, 7}, {3, 4, 7}, {3, 5, 6}. Définissons la relation d'incidence comme la partie de formée par les couples (P, L) tels que On vérifie facilement qu'alors est un plan de Fano.
Le graphique qui suit donne un exemple de plan de Fano :
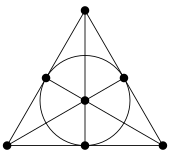 Une représentation du plan de Fano (les six segments et le cercle représentent les 7 lignes).
Une représentation du plan de Fano (les six segments et le cercle représentent les 7 lignes).
(i) Tous les plans de Fano sont isomorphes (comme structures d'incidence).
(ii) Plus précisément : si et sont deux plans de Fano, si est un triple de points non alignés dans , si est un triple de points non alignés dans , alors il y a un unique isomorphisme de sur qui applique sur , sur et sur .
(iii) Le groupe des automorphismes d'un plan de Fano est d'ordre 168. (La structure de ce groupe sera précisée plus loin.)
Démontrons l'assertion d'existence du point (ii).
Soit un plan de Fano, soient trois points non alignés de ce plan (on choisit cette numérotation pour être en harmonie avec l'exemple 16). On se ramène facilement à prouver qu'il existe un isomorphisme du plan de Fano considéré à l'exemple 16 sur qui applique 1 sur , 2 sur et 4 sur .
La ligne passe par un unique troisième point, soit Puisque, par hypothèse, et ne sont pas alignés, n'est pas sur la ligne et est donc distinct de et
De même, il y a un unique troisième point, soit , sur la ligne . Le point n'est pas égal à , car dans le cas contraire, serait sur la ligne , ce qui est faux, puisque et sont supposés non alignés. n'est pas non plus égal à , car dans le cas contraire, serait sur la ligne , autrement dit serait sur la ligne alors que et sont supposés non alignés.
Donc est distinct de .
De même, il y a un unique troisième point, soit , sur la ligne Ce point est distinct des points . (Si , alors est sur , autrement dit est sur , ce qui est faux, puisque et sont supposés non alignés. est distinct de par définition de Si , alors est sur , autrement dit est sur , ce qui est faux, puisque et sont supposés non alignés. est distinct de par définition de . Si , alors est sur , autrement dit est sur ; d'après la définition de donc est sur , ce qui est faux, puisque et sont supposés non alignés.)
Désignons par le point distinct de Par définition de ces points, comprend des lignes et (où on représente une ligne par les trois points qui se trouvent dessus). D'après la définition d'un plan de type projectif, il y a une et une seule ligne joignant et Cette ligne doit passer par un troisième point et ce point doit être distinct de et (si c'était , alors et seraient tous deux sur la ligne , donc cette ligne comprendrait au moins 4 points, contradiction; les autres cas sont semblables), donc ce point doit être De même, la ligne joignant et passe par et la ligne joignant et passe elle aussi par Donc l'ensemble de lignes comprend encore et
Nous avons donc trouvé six des sept lignes de , à savoir et Mais nous n'avons pas encore de ligne joignant et ni de ligne joignant et Donc la ligne restante doit être et les sept lignes de sont
- et
Désignons par f la bijection de {1, ... , 7} sur et par g la bijection de l'ensemble des lignes du plan de Fano de l'exemple 16 sur Le couple (f, g) est un isomorphisme (de structures d'incidence) du plan de Fano de l'exemple 16 sur le plan de Fano
Nous avons donc prouvé l'assertion d'existence du point (ii). Prouvons maintenant l'assertion d'unicité.
On se ramène facilement à prouver que si est le plan de Fano de l'exemple 16, si est un plan de Fano quelconque, si sont trois points non alignés de il existe au plus un isomorphisme de sur qui applique 1 sur R1, 2 sur R2 et 4 sur R4.
Soit (f, g) un tel isomorphisme. Alors, puisque {1, 2, 3} est une ligne de f doit appliquer 3 sur l'unique point de la ligne qui est distinct de et de Désignons par ce troisième point de la ligne Donc
De même, puisque {1, 4, 5} est une ligne de f doit appliquer 5 sur l'unique point de la ligne qui est distinct de et de Désignons par ce troisième point de la ligne Donc
De même, puisque {2, 4, 6} est une ligne de f doit appliquer 6 sur l'unique point de la ligne qui est distinct de et de Désignons par R_{6} ce troisième point de la ligne R_{2}R_{4}. Donc f(6) = R_{6}.
Puisque f est une bijection et que 1, 2, 3, 4, 5, 6 sont distincts, et sont distincts. Donc si désigne l'unique point de distinct de ,
Donc la valeur de f en chacun des points 1, 2, 3, 4, 5, 6, 7 est déterminée de façon unique. Comme noté, la bijection g est déterminée par f, donc l'isomorphisme (f, g) est déterminé de façon unique. Nous avons donc prouvé l'assertion d'unicité du point (ii).
Il résulte du point (ii) qu'un plan de Fano a exactement autant d'automorphismes qu'il a de triples de points non alignés. L'ensemble des triples de points non alignés est
où désigne l'ensemble des trois points qui sont sur la ligne PQ. On en tire facilement qu'il y a exactement triples de points non alignés, donc un plan de Fano a exactement 168 automorphismes, ce qui achève de démontrer l'énoncé.
Puisque les plans de Fano sont tous isomorphes, on dit volontiers « le plan de Fano » plutôt que « un plan de Fano ».
Soit une structure d'incidence telle qu'il y ait exactement 7 points et 7 lignes, que chaque point soit exactement sur 3 lignes, que chaque ligne passe exactement par 3 points, que pour chaque paire de points distincts, il y ait au plus une ligne qui passe à la fois par ces deux points et que pour chaque paire de lignes distinctes, il y ait au plus un point qui soit à la fois sur ces deux lignes. Alors est un plan de Fano.
Soit Y l'ensemble des parties à deux éléments de
Alors
Soit X l'ensemble des couples (C, L) tels que C soit une paire appartenant à Y, que L soit un élément de et que C soit sur L, où nous disons que C est sur L si les deux points de C sont sur L. Pour chaque ligne L dans il y a, par hypothèse, exactement 3 points sur L, donc exactement paires de points distincts sur L. Donc
Considérons l'application qui applique (C, L) sur C. Le nombre des préimages de C dans Y est exactement le nombre de lignes sur lesquelles la paire C se trouve. Puisque, par hypothèse, chaque paire de points distincts est au plus sur une ligne, l'application est injective. Puisque , cette application doit être bijective. Donc
- (1) chaque paire de points distincts est sur exactement une ligne.
Les hypothèses sur la structure étant également satisfaites par sa structure duale, nous avons de même :
- (2) pour toute paire de lignes distinctes, il y a un et un seul point qui se trouve à la fois sur ces deux lignes.
Prouvons maintenant que
- (3) contient un ensemble de 4 points dont 3 ne sont jamais alignés.
Choisissons deux points distincts P et Q et choisissons un point R qui n'est pas sur l'unique ligne joignant P et Q (puisqu'il y a exactement 3 points sur cette ligne, on a le choix parmi quatre points). Il y a exactement 7 points dans , donc il y a un (unique) point S qui est distinct de P, de Q, de R, de l'unique point de PQ autre que P et Q, de l'unique point de PR autre que P et R, et de l'unique point de QR autre que Q et R. Alors les points P, Q, R et S forment l'ensemble désiré.
Les relations (1), (2) et (3) montrent que est un plan de type projectif. D'après les hypothèses de l'énoncé, c'est donc un plan de Fano, ce qui démontre le théorème.
Section 3. Groupes simples d'ordre 168
On va démontrer que les groupes simples d'ordre 168 sont tous isomorphes au groupe des automorphismes du plan de Fano. Puisque, d'après le chapitre sur la simplicité des groupes linéaires spéciaux projectifs, PSL(2, 7) est un groupe simple d'ordre 168, et qu'il existe donc au moins un groupe simple d'ordre 168, il en résultera que le groupe des automorphismes du plan de Fano est un groupe simple d'ordre 168.
Soit G un groupe simple d'ordre 168, soit H un sous-groupe propre de G. L'indice de H dans G est au moins égal à 7. (Autrement dit, l'ordre de H est au plus égal à 24.)
Désignons par k l'indice de H dans G. D'après le préliminaire 1, l'ordre 168 de G divise k!. Donc, puisque 168 est divisible par 7, 7 divise k!, donc
Soit G un groupe simple d'ordre 168. Pour tout diviseur premier p de l'ordre 168 de G,
Soit P un p-sous-groupe de Sylow de G. G, étant d'ordre 168, n'est pas un p-groupe, donc P est un sous-groupe propre de G ; de plus, puisque p divise l'ordre de G, P n'est pas réduit à l'élément neutre. Puisque G est simple, P n'est donc pas normal dans G. Le normalisateur de P dans G est donc un sous-groupe propre de G. Donc, d'après l'étape 1, l'indice de dans G est au moins égal à 7. Mais l'indice de dans G est d'où l'énoncé.
Soit G un groupe simple d'ordre 168. Alors
(i) ;
(ii) pour tout 7-sous-groupe de Sylow P de G.
(On verra à l'étape 4 que G n'a pas d'élément d'ordre 21, donc n'est pas cyclique. Cela détermine la structure de , vu la classification des groupes d'ordre pq, p et q nombres premiers distincts, que nous avons obtenue dans les exercices Produit semi-direct. Mais cela ne nous servira pas.)
D'après les théorèmes de Sylow, divise 24 et donc est égal à 1 ou à 8. D'après l'étape 2, ne peut pas être égal à 1, donc ce qui est la première assertion de l'énoncé. La seconde assertion résulte de la première.
Soit G un groupe simple d'ordre 168. G n'a pas d'éléments d'ordre 21.
Voici d'abord une démonstration qui repose sur le théorème du complément normal de Burnside. Supposons que, par absurde, g soit un élément d'ordre 21 de G. Alors le groupe H = < g >, qui est d'ordre 21, contient un sous-groupe P d'ordre 7 (théorème de Sylow, de Cauchy ou simplement le fait que H est cyclique). Puisque H est cyclique et donc abélien, P est normal dans H, autrement dit H est contenu dans . D'après l'étape 3, a le même ordre que H, à savoir 21, donc donc est abélien, donc, d'après le théorème du complément normal de Burnside, P a un complément normal dans G, ce qui est impossible puisque G est simple.
Voici maintenant une démonstration qui ne repose pas sur le théorème du complément normal de Burnside. Comme dans la première démonstration, supposons que, par absurde, g soit un élément d'ordre 21 de G. Alors le groupe H = < g >, qui est d'ordre 21, contient un sous-groupe Q d'ordre 3. (Sylow, Cauchy ou simplement le fait que H est cyclique.) Puisque H est cyclique et donc abélien, Q est normal dans H, donc Dès lors, l'indice divise [G : H] = 8. Mais Q est un 3-sous-groupe de Sylow de G, donc, d'après les théorèmes de Sylow, Donc doit être égal à 1 ou à 4, ce qui, dans les deux cas, contredit l'étape 2, selon laquelle
Soit G un groupe simple d'ordre 168. G n'a pas d'éléments d'ordre 14.
Supposons que, par absurde, g soit un élément d'ordre 14 de G. Alors <g> contient un (unique) sous-groupe d'ordre 7, soit P. Puisque <g> est commutatif, il est contenu dans et a fortiori dans . Mais P est un 7-sous-groupe de Sylow de G, donc, d'après l'étape 3, <g> est contenu dans un sous-groupe d'ordre 21 de G. Puisque l'ordre 14 de <g> ne divise pas 21, cela contredit le théorème de Lagrange.
Soit G un groupe simple d'ordre 168. Pour tout 7-sous-groupe de Sylow de G, comprend exactement 14 éléments d'ordre 3.
Soit P un 7-sous-groupe de Sylow de G ; posons N = N_{G}(P). D'après les étapes 3 et 4, et tout élément de N est d'ordre 1, 3 ou 7. Puisque P est normal dans N (par définition du normalisateur), donc N comprend exactement 6 éléments d'ordre 7. L'élément neutre est le seul élément d'ordre 1, donc les 21 - 6 - 1 = 14 éléments restants de N sont tous d'ordre 3.
Soit G un groupe simple d'ordre 168.
(i) ;
(ii) pour tout 3-sous-groupe de Sylow Q de G, est isomorphe à (et à ).
D'après les théorèmes de Sylow, divise 56 et est ≡ 1 (mod 3), donc est un des nombres 1, 4, 7, 28. D'après l'étape 2, est au moins égal à 7, donc est égal à 7 ou à 28. Supposons que Alors, puisque chaque 3-sous-groupe de Sylow de G comprend exactement 2 éléments d'ordre 3 et que l'intersection de deux différents sous-groupes d'ordre 3 est toujours triviale, il y a exactement 2 · 7 = 14 éléments d'ordre 3 dans G. Donc, d'après l'étape 6, tout élément d'ordre 3 de G appartient à chaque , P parcourant les 7-sous-groupes de Sylow de G. Donc
- (1)
D'autre part, est contenu dans pour tout P et donc pour au moins un P, donc, d'après l'étape 3,
- (2)
Comme est un sous-groupe normal de G (voir un exercice de la série Théorèmes de Sylow) les relations (1) et (2) contredisent la simplicité de G.
Donc donc, d'après ce qu'on a vu,
D'après les théorèmes de Sylow, pour tout Q dans donc
- pour tout 3-sous-groupe de Sylow de G.
D'après le théorème du complément normal de Burnside, n'est pas abélien, donc, étant d'ordre 6, il est isomorphe à (Rappel : on a vu dans un exercice de la série Groupes diédraux que si p est un nombre premier impair, tout groupe non abélien d'ordre 2p est diédral et que est isomorphe à )
Soit G un groupe simple d'ordre 168. G n'a pas d'élément d'ordre 6.
Un tel élément g engendrerait un sous-groupe cyclique d'ordre 6 de R désignant l'unique 3-sous-groupe de Sylow de <g>. C'est impossible, puisque, d'après l'étape 7, est un groupe d'ordre 6 non abélien.
Soit G un groupe simple d'ordre 168. (Par exemple d'après l'étape 2, G a plus d'un 2-sous-groupe de Sylow, de sorte qu'on peut parler du plus grand ordre possible pour l'intersection de deux différents 2-sous-groupes de Sylow de G.) Soient P et Q deux différents 2-sous-groupes de Sylow de G tels que soit le plus grand possible. Alors
- (i) est un groupe de Klein ;
- (ii) est isomorphe à
En particulier,
- (iii) le plus grand ordre possible pour l'intersection de deux différents 2-sous-groupes de Sylow de G est 4.
D'après les théorèmes de Sylow, divise 21. D'après l'étape 2, donc doit être égal à 7 ou à 21.
(En particulier, G a plus d'un 2-sous-groupe de Sylow, de sorte qu'on peut parler du plus grand ordre possible pour l'intersection de deux différents 2-sous-groupes de Sylow de G.)
Dans les deux cas, n'est pas congru à 1 modulo 8, donc, d'après le préliminaire 2 et la maximalité de , nous avons
Puisque est un sous-groupe propre de P, l'ordre de divise 4 ; de plus, nous avons vu que est distinct de 1, donc
- est d'ordre 2 ou 4.
Posons Prouvons que
- (thèse 1) divise 24.
Puisque divise 168, il suffit de prouver que
- (thèse 2) 7 ne divise pas .
Soit C le sous-groupe de Puisque il suffit, pour prouver la thèse (2), de prouver que 7 ne divise ni [N : C] ni .
D'après le lemme N/C (chapitre Conjugaison, centralisateur, normalisateur), N/C est isomorphe à un sous-groupe de donc l'ordre [N : C] de N/C divise l'ordre de Mais on a vu que est d'ordre 2 ou 4, donc compte au plus 4 éléments, donc l'ordre de divise 24, donc [N : C] divise 24 et n'est donc pas divisible par 7.
Supposons maintenant que, par absurde, 7 divise . Alors C comprend un élément g d'ordre 7. Par définition de C, g commute avec tout élément de . On a vu que est d'ordre 2 ou 4, donc il comprend un élément d'ordre 2, soit h. Alors g et h commutent, donc gh est d'ordre 14, ce qui contredit l'étape 5.
Donc n'est pas divisible par 7. Nous avons donc prouvé la thèse (1), à savoir que
- (3) divise 24.
Montrons que est divisible par 4.
est un sous-groupe de P, donc son ordre est une puissance de 2 ; de plus, d'après le préliminaire 3, contient strictement ; or on a vu que est égal à 2 ou à 4, donc
- (4) est divisible par 4.
D'après le préliminaire 3, N a au moins 2 différents 2-sous-groupes de Sylow. D'après les théorèmes de Sylow et le résultat (3), divise 3, donc :. Toujours d'après les théorèmes de Sylow et le résultat (3), divise 8 et donc égale 1 ou 4. D'autre part, puisqu'on vient de montrer que , l'ordre de N est divisible par 3 ; donc si , N a un sous-groupe normal R d'ordre 3 ; alors ce qui est impossible, puisque, d'après l'étape 7, et que, comme on l'a vu en (4), est divisible par 4. Donc Ainsi, N est un groupe d'ordre divisant 24, avec et donc, d'après le préliminaire 5,
- (5) N est isomorphe à
ce qui prouve l'assertion (ii) de l'énoncé.
Rappelons qu'on a posé
où est un groupe d'ordre 2 ou 4.
Donc est un 2-sous-groupe normal non trivial de Mais d'après le préliminaire 7, le seul 2-sous-groupe normal non trivial de est un groupe de Klein, donc est un groupe de Klein. Cela prouve les points (i) et (iii) de l'énoncé et achève donc la démonstration.
Soit G un groupe simple d'ordre 168. Les 2-sous-groupes de Sylow de G sont isomorphes à et sont en nombre 21. Chaque 2-sous-groupe de Sylow de G est son propre normalisateur dans G.
Puisque les 2-sous-groupes de Sylow de sont isomorphes au groupe diédral d'ordre 8 (voir préliminaire 6) et que, d'après l'étape 9, G a au moins un sous-groupe isomorphe à S_{4}, G contient au moins un sous-groupe isomorphes à Un tel sous-groupe, étant d'ordre 8, est un 2-sous-groupe de Sylow de G, donc les 2-sous-groupes de Sylow de G sont isomorphes à
Prouvons que Soit P un 2-sous-groupe de Sylow de G. L'indice de dans G divise 168/8 = 21 et, d'après l'étape 1, il est au moins égal à 7. Il est donc égal à 7 ou à 21 (on l'a déjà noté au début de la démonstration de l'étape 9). Supposons que, par absurde, cet indice soit égal à 7. Alors est d'ordre 24. Nous pouvons donc choisir un sous-groupe Q d'ordre 3 de . Puisque P est normal dans , Q opère sur P par conjugaison. Notons f l'homomorphisme correspondant de Q dans Aut(P), c'est-à-dire l'homomorphisme de Q dans Aut(P) qui applique un élément x de Q sur l'automorphisme de P. D'après le premier théorème d'isomorphisme, l'image de f est isomorphe à un quotient de Q et est donc d'ordre 3 ou 1. Mais on vient de voir que P est isomorphe à ce qui entraîne que Aut(P) est isomorphe à D'après le préliminaire 9, il en résulte que l'ordre de Aut(P) n'est pas divisible par 3. Donc l'homomorphisme f de Q dans Aut(P) est trivial, ce qui revient à dire que Q centralise P. Donc, si nous choisissons un élément d'ordre 2 dans P et un élément d'ordre 3 dans Q, le produit de ces deux éléments est d'ordre 6, ce qui contredit l'étape 8. Donc est d'indice 21 dans G, ce qui revient à dire que
(On verra une autre démonstration de à l'étape 17.)
Puisque est d'indice 21 dans G, il est d'ordre 8, donc ce qui achève de démontrer l'énoncé.
Soit G un groupe simple d'ordre 168. G n'a pas d'élément d'ordre 8.
Un tel élément engendrerait un 2-sous-groupe de Sylow de G cyclique, ce qui contredit l'étape 10.
Soit G un groupe simple d'ordre 168. Tout élément de G est d'ordre 1, 2, 3, 4 ou 7.
D'après les étapes 4, 5, 8 et 11, G n'a pas d'élément d'ordre 6, 8, 14 ou 21 et n'a donc pas d'élément d'ordre divisible par 6, 8, 14 ou 21. Comme les seuls facteurs premiers possibles pour l'ordre d'un élément de G sont 2, 3 et 7, il en résulte que tout élément de G est d'ordre 1, 2, 3, 4 ou 7.
Soit G un groupe simple d'ordre 168. G a exactement 56 éléments d'ordre 3, formant une seule classe de conjugaison.
D'après l'étape 7, les 3-sous-groupes de Sylow de G sont en nombre 28. Puisqu'ils sont d'ordre premier, ils se coupent trivialement deux à deux. Comme chacun d'eux comprend 2 éléments d'ordre 3 et que tout élément d'ordre 3 de G est évidemment contenu dans un de ces sous-groupes, G a exactement 56 éléments d'ordre 3.
Si P est un 3-sous-groupe de Sylow de G, il résulte de l'étape 7 que est d'ordre 6. Donc P est abélien et son indice dans est un nombre premier. D'après le préliminaire 8, il en résulte que C_{G}(P) est égal à P et est donc d'indice 56 dans G. Cela revient à dire que pour tout élément g d'ordre 3 de G, est d'indice 56 dans G, autrement dit les conjugués de g dans G sont en nombre 56. L'énoncé en résulte.
Pour prouver que tous les éléments d'ordre 3 de G sont conjugués dans G, on a utilisé le préliminaire 8, qui repose sur le théorème du complément normal de Burnside et donc sur la théorie du transfert. Voici une démonstration qui ne dépend pas de la théorie du transfert.
Si P est un 3-sous-groupe de Sylow de G, les deux éléments d'ordre 3 de P sont conjugués dans (en effet, on a vu à l'étape 7 que et les éléments d'ordre 3 de sont conjugués dans puisqu'ils ont la même structure cyclique). A fortiori, les deux éléments d'ordre 3 de P sont conjugués dans G. Puisque tous les 3-sous-groupes de Sylow de G sont conjugués dans G, on en tire facilement que tous les éléments d'ordre 3 de G sont conjugués dans G.
Soit G un groupe simple d'ordre 168. G a exactement 48 éléments d'ordre 7, répartis en deux classes de conjugaison de 24 éléments chacune.
On a vu à l'étape 3 que les 7-sous-groupes de Sylow de G sont en nombre 8. Ces sous-groupes, étant d'ordre premier, se coupent trivialement deux à deux et chacun d'eux comprend exactement 6 éléments d'ordre 7, donc la réunion de ces sous-groupes comprend exactement 48 éléments d'ordre 7. Comme tout élément d'ordre 7 de G appartient à un de ces sous-groupes, G a exactement 48 éléments d'ordre 7.
Si P est un 7-sous-groupe de Sylow de G, il résulte de l'étape 3 que est d'ordre 21. Donc P est abélien et son indice dans est un nombre premier. D'après le préliminaire 8, il en résulte que est égal à P et est donc d'indice 24 dans G. Cela revient à dire que pour tout élément g d'ordre 7 de G, est d'indice 24 dans G, autrement dit les conjugués de g dans G sont en nombre 24. L'énoncé en résulte.
Pour prouver que les conjugués d'un élément d'ordre 7 de G sont en nombre 24, on a utilisé le préliminaire 8, qui repose sur le théorème du complément normal de Burnside et donc sur la théorie du transfert. Voici une démonstration qui ne dépend pas de la théorie du transfert. Si g est un élément d'ordre 7 de G, le centralisateur de g dans G est contenu dans le normalisateur de <g> dans G, normalisateur qui, d'après l'étape 3, est d'ordre 21. Donc l'ordre du centralisateur de g dans G divise 21. D'après l'étape 4 (ou 12), G n'a pas d'élément d'ordre 21, donc le centralisateur de g dans G n'a pas d'élément d'ordre 3 (car le produit de g par un tel élément d'ordre 3 serait un élément d'ordre 21), donc l'ordre du centralisateur de g n'est pas divisible par 3 et divise donc 7. Puisque ce centralisateur contient évidemment <g>, il est égal à <g> et est donc d'ordre 7, donc la classe de conjugaison de g est de cardinal 24, d'où l'énoncé.
Soit G un groupe simple d'ordre 168. G comprend exactement 105 éléments d'ordre impair.
D'après l'étape 12, les éléments d'ordre impair de G sont ses éléments d'ordre 1, 3 ou 7. D'après les étapes 13 et 14,il y a 56 éléments d'ordre 3 et 48 éléments d'ordre 7, donc en tout 1 + 56 + 48 = 105 éléments d'ordre impair.
Soit G un groupe simple d'ordre 168. G comprend exactement 42 éléments d'ordre 4, formant une seule classe de conjugaison.
Soit P un 2-sous-groupe de Sylow de G. D'après l'étape 10, P est isomorphe à Il comprend donc exactement 2 éléments d'ordre 4. De plus, ces deux éléments sont conjugués dans P (car n'importe quel élément de qui n'appartient pas au sous-groupe cyclique C d'ordre 4 de envoie par conjugaison un élément g de C sur g^{-1}),
donc ils sont a fortiori conjugués dans G. Puisque tous les 2-sous-groupe de Sylow de G sont conjugués dans G, il en résulte que tous les éléments d'ordre 4 de G sont conjugués dans G.
D'autre part, si P et Q sont deux différents 2-sous-groupes de Sylow de G, ne comprend aucun élément d'ordre 4 (voir étape 9), donc chaque élément d'ordre 4 appartient à un et un seul 2-sous-groupe de Sylow P. En considérant l'application qui envoie chaque élément a d'ordre 4 de G sur l'unique 2-sous-groupe de Sylow de G qui comprend a, en tenant compte que, d'après l'étape 10, les 2-sous-groupes de Sylow de G sont en nombre 21 et en appliquant le principe des bergers, on trouve que G comprend exactement 42 éléments d'ordre 4, ce qui achève la démonstration.
Soit G un groupe simple d'ordre 168. G comprend exactement 21 éléments d'ordre 2, formant une seule classe de conjugaison.
Soit P un 2-sous-groupe de Sylow de G. D'après l'étape 10, P est isomorphe à donc, d'après le préliminaire 10, le centre Z(P) de P est un groupe d'ordre 2. Puisque Z(P) est caractéristique dans P et P normal dans , Z(P) est normal dans . Puisque tout sous-groupe normal d'ordre 2 est central, Z(P) est central dans . Donc tout élément de commute avec l'élément non neutre z de Z(P), donc
- (1)
Mais z ne commute avec aucun élément non neutre d'ordre impair. En effet, dans le cas contraire, z commuterait avec un élément d'ordre 3 ou avec un élément d'ordre 7 (on peut le déduire de l'étape 12, mais aussi du simple fait que les seuls diviseurs premiers impairs de l'ordre de G sont 3 et 7). Or si z commutait avec un élément g d'ordre 3, zg serait d'ordre 6, ce qui contredit l'étape 8, et si z commutait avec un élément g d'ordre 7, alors zg serait d'ordre 14, ce qui contredit l'étape 5. Donc ne comprend aucun élément non neutre d'ordre impair, donc divise 8, donc (1) donne
- (2)
(Il en résulte que pour tout 2-sous-groupe de Sylow P de G, d'où Nous avons donc ici une nouvelle démonstration de ces deux résultats déjà prouvés à l'étape 10.)
D'après (2), donc z a exactement 21 conjugués dans G. Donc
- (3) G contient au moins une classe de conjugaison formée de 21 éléments d'ordre 2.
En particulier, G a au moins 21 éléments d'ordre 2 dans G.
Nous avons donc trouvé jusqu'ici 105 éléments d'ordre impair (étape 15), 42 éléments d'ordre 4 (étape 16) et 21 éléments d'ordre 2. Puisque 105 + 21 + 42 = 168, nous avons donc trouvé tous les éléments de G. Donc, compte tenu de (3), G comprend exactement 21 éléments d'ordre 2, tous conjugués les uns des autres, ce qui démontre l'énoncé.
Soit G un groupe simple d'ordre 168, soit U un sous-groupe de Klein de G. Alors est isomorphe à Les sous-groupes de Klein de G sont en nombre 14 et se répartissent en deux classes de conjugaison comprenant chacune 7 sous-groupes. Chaque 2-sous-groupe de Sylow de G contient un représentant de chacune de ces deux classes.
Il résulte de l'étape 17 que le centralisateur dans G d'un élément d'ordre 2 est toujours d'indice 21 dans G et est donc d'ordre 8, autrement dit est un 2-sous-groupe de Sylow de G. Donc, d'après l'étape 10, le centralisateur dans G d'un élément d'ordre 2 est un groupe diédral d'ordre 8.
Soit U un sous-groupe de Klein de G, soient u et v deux différents éléments non neutres de U. Alors, d'après ce qu'on vient de noter, et sont deux 2-sous-groupes de Sylow de G.
Ils sont distincts, car un groupe diédral d'ordre 8 n'a qu'un élément central d'ordre 2 (voir préliminaire 10).
Ils contiennent tous deux U, puisque U est commutatif. Donc
- (1)
Puisque le groupe est l'intersection de deux différents sous-groupes d'ordre 8, il est d'ordre au plus 4, donc la relation (1) doit être une égalité :
Il résulte donc de l'étape 9 que pour tout sous-groupe de Klein U de G,
- (2) est isomorphe à et, en particulier, est d'ordre 24.
Donc
- (3) U a exactement 7 conjugués.
Fixons un 2-sous-groupe de Sylow P de G. D'après les théorèmes de Sylow, U est contenu dans un 2-sous-groupe de Sylow Q de G et Q est conjugué de P dans G. Donc
- (4) U est conjugué dans G d'un sous-groupe de Klein de P, soit V.
D'après le préliminaire 11, P contient exactement deux sous-groupes de Klein et ces deux sous-groupes ne sont pas conjugués dans P.
Désignons par W celui qui est distinct de V. Puisque (voir étape 10), dire que V et W ne sont pas conjugués dans P revient à dire que V et W ne sont pas conjugués dans . Donc, d'après le préliminaire 4 (et compte tenu que V et W, étant d'indice 2 dans P, sont normaux dans P),
- (5) V et W ne sont pas conjugués dans G.
Donc, d'après (4), U est conjugué dans G d'un et d'un seul des deux sous-groupes de Klein de P. Les sous-groupes de Klein de G se répartissent donc en deux classes de conjugaison. Joint à (2), à (3) et à (5), cela démontre l'énoncé.
Notation. G étant un groupe simple d'ordre 168, on notera et les deux classes de conjugaison de sous-groupes de Klein de G (voir étape 18). On appellera « points » les éléments de et « lignes » les éléments de . On définit une relation d'incidence en disant qu'un point P est sur une ligne L (c'est-à-dire (P, L) appartient à ) s'il existe un 2-sous-groupe de Sylow de G qui contient à la fois P et L. Un tel 2-sous-groupe de Sylow de G est alors engendré par P et L (préliminaire 11, étape 10 et le fait que P et L, n'étant pas conjugués, sont distincts), et est donc l'unique 2-sous-groupe de Sylow de G qui contient à la fois P et L.
Soit G un groupe simple d'ordre 168. La structure d'incidence est un plan de Fano.
Si P est sur L, alors P est normal dans le 2-sous-groupe de Sylow R contenant P et L, donc Réciproquement, si alors <P, L> est un 2-sous-groupe de Sylow de G, donc P est sur L. Donc
- (1) P est sur L
Soit P un point, soit L une ligne passant par P. Comme noté à propos de la définition de la relation d'incidence, <P, L> est un 2-sous-groupe de Sylow de G, autrement dit (étape 10) un sous-groupe diédral d'ordre 8 de G. Le point P étant fixé, considérons l'application de l'ensemble des lignes passant par P dans l'ensemble des 2-sous-groupes de Sylow de G contenant P. Puisque, d'après le préliminaire 11, un groupe diédral d'ordre 8 n'a que deux sous-groupes de Klein,
- est injective.
Prouvons qu'elle est surjective. Il revient au même de prouver que si P est un sous-groupe de Klein de G, si D est un 2-sous-groupe de Sylow de G contenant P, alors il existe un sous-groupe de Klein L de G, non conjugué de P dans G, tel que D = <P, L>. D'après le préliminaire 11, il existe un sous-groupe de Klein K de G, non conjugué de P dans D, tel que D = <P, K> et tout revient à prouver que K n'est pas conjugué de P dans G. P et K sont d'indice 2 dans D, donc normaux dans D ; de plus, D est un 2-sous-groupe de Sylow de G. Donc si P et K étaient conjugués dans G, ils seraient conjugués dans (voir préliminaire 4). Mais d'après l'étape 10, Donc si P et K étaient conjugués dans G, ils seraient conjugués dans D, contradiction. Donc est surjective et donc bijective. Donc le nombre des lignes passant par P est égal au nombre des 2-sous-groupes de Sylow de G qui contiennent P. Un tel 2-sous-groupe de Sylow de G normalise P (puisque P en est sous-groupe d'indice 2), donc le nombre des 2-sous-groupes de Sylow de G qui contiennent P est égal au nombre des 2-sous-groupes de Sylow de qui contiennent P. Puisque est isomorphe à (voir étape 18), il contient exactement trois 2-sous-groupes de Sylow de G (voir Préliminaire 12 (ii)), lesquels contiennent tous P (puisque P est un 2-sous-groupe normal de ). Donc
- (2) chaque point P est exactement sur 3 lignes.
De même,
- (3) chaque ligne L passe par exactement 3 points.
Soient P et Q deux points distincts. Si P et Q sont tous deux sur une ligne L, alors, d'après (1), P et Q sont tous deux des sous-groupes de Ils sont tous deux non normaux dans En effet, L est normal dans qui est isomorphe à et on sait que ne contient qu'un sous-groupe de Klein normal (voir préliminaire 7) ; donc L est le seul sous-groupe de Klein normal de ; donc P et Q, qui sont distincts de L, sont non normaux dans
D'après le préliminaire 12, deux sous-groupes de Klein non normaux de engendrent toujours donc Donc L est l'unique sous-groupe de Klein normal de <P, Q>, donc P et Q déterminent L de façon unique. Donc
- (4) toute paire de points distincts est sur au plus une ligne.
Les hypothèses que nous avons utilisées pour obtenir ce résultat étant également satisfaites par la structure d'incidence duale, nous avons de même
- (5) pour toute paire de lignes distinctes, il y a au plus un point qui se trouve à la fois sur ces deux lignes.
D'après le préliminaire 18 (et compte tenu que, d'après l'étape 18, il y a exactement 7 points et 7 lignes), il résulte de (2), (3), (4) et (5) que est un plan de Fano, ce qui démontre l'énoncé.
Soit G un groupe simple d'ordre 168. G est isomorphe à le groupe des automorphismes du plan de Fano.
Comme plus haut, désignons par l'ensemble des sous-groupes de Klein de G appartenant à une première classe de conjugaison, désignons par l'ensemble des sous-groupes de Klein de G appartenant à l'autre classe de conjugaison et désignons par la partie de formée par les couples (P, L) tels que P et L soient contenus dans un même 2-sous-groupe de Sylow de G. Posons D'après l'étape 19, est un plan de Fano. Pour tout élément g de G, la conjugaison par g fournit un automorphisme du plan de Fano : elle applique bijectivement points sur points, lignes sur lignes et préserve la relation d'incidence. Donc la conjugaison fournit une application
qui, comme on le vérifie facilement, est un homomorphisme de groupes. Il est clair que cet homomorphisme n'est pas trivial (par exemple parce que les 7 points sont des sous-groupes conjugués), donc son noyau est un sous-groupe normal propre de G ; puisque G est simple, ce noyau doit donc être trivial, autrement dit l'homomorphisme est injectif. D'après le préliminaire 17, est d'ordre 168 et a donc le même ordre que G, donc l'homomorphisme est un isomorphisme, d'où l'énoncé.
Tous les groupes simples d'ordre 168 sont isomorphes. Le groupe des automorphismes d'un plan de Fano est un groupe simple d'ordre 168.
La première assertion résulte de l'étape 20. Puisque, d'après le chapitre Simplicité des groupes linéaires spéciaux projectifs, le groupe PSL(2, 7) est un groupe simple d'ordre 168, de sorte qu'il existe au moins un groupe simple d'ordre 168, il résulte de l'étape 20 que le groupe des automorphismes du plan de Fano est un groupe simple (d'ordre 168).
Notes et références
- ↑ Jacqueline Lelong-Ferrand], Fondements de la géométrie, PUF, 1985, p. 162.