Sommation/Séries de Fourier et fonction zêta

Le but de ce chapitre est de présenter certaines techniques de sommation qui vont nous permettre de calculer des sommes que nous n'aurions pas pu calculer avec les techniques des chapitres précédents. Pour cela, nous allons utiliser deux résultats importants issus des séries de Fourier. Il n'est bien sûr, pas question d'exposer en détail la théorie sur les séries de Fourier. Les lecteurs intéressés peuvent, avec profit, commencer par étudier la leçon : Série de Fourier. Nous étudierons aussi, dans ce chapitre, la fonction zêta de Riemann dont certaines de ses valeurs peuvent être calculées grâce aux séries de Fourier. Ce chapitre permet de compléter logiquement la leçon sur les sommations, mais l'étudiant pourra ne pas l'étudier si les séries de Fourier ne figurent pas dans son programme.

Les deux théorèmes fondamentaux

Soit f une fonction intégrable et 2π-périodique de l’ensemble des nombres réels dans l’ensemble des nombres réels (éventuellement complexes).

Pour tout entier naturel $n$ , on appellera coefficients de Fourier trigonométriques, les deux nombres :

$a_{n}(f)={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(nt)\mathrm {d} t$

$b_{n}(f)={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(nt)\mathrm {d} t$

nous admettrons alors les deux théorèmes suivants :

Théorème de Dirichlet

Si f est C¹ par morceaux, alors :

${\frac {a_{0}(f)}{2}}+\sum _{n=1}^{\infty }\left(a_{n}(f)\cos(nx)+b_{n}(f)\sin(nx)\right)={\frac {f(x^{+})+f(x^{-})}{2}}$

Formule de Parseval

Si f est continue par morceaux, alors :

${\frac {(a_{0}(f))^{2}}{2}}+\sum _{n=1}^{\infty }\left(|a_{n}(f)|^{2}+|b_{n}(f)|^{2}\right)={\frac {1}{\pi }}\int _{0}^{2\pi }|f(t)|^{2}\mathrm {d} t$

Nous remarquons, dans ces deux théorèmes, des sommations. Par un choix convenable de la fonction f et de la valeur de x, nous allons pouvoir calculer des sommes particulières. Nous verrons cela en exercices.

Étude de la fonction zêta

Définition

Nous allons voir un exemple de fonction définie par une somme :

Définition de la fonction zêta de Riemann

La fonction zêta, notée ζ, est définie par la somme suivante :

$\forall x\in \left]1,+\infty \right[\qquad \zeta (x)=\sum _{k=1}^{\infty }{\frac {1}{k^{x}}}$ .

La fonction zêta est bien définie sur l'intervalle $\left]1,+\infty \right[$ car c’est une série de Riemann.

Dérivées successives de la fonction zêta

Propriété

$\forall n\in \mathbb {N} \quad \forall x\in \left]1,+\infty \right[\qquad \zeta ^{(n)}(x)=(-1)^{n}\sum _{k=1}^{\infty }{\frac {\ln ^{n}(k)}{k^{x}}}$ .

Démonstration

Notons $f_{n}$ la fonction $x\mapsto \sum _{k=1}^{\infty }{\frac {\ln ^{n}(k)}{k^{x}}}$ (qui est bien définie sur $\left]1,+\infty \right[$ , comme série de Bertrand). En particulier, $f_{0}=\zeta =\zeta ^{(0)}$ donc, pour établir par récurrence la propriété ci-dessus, il s'agit de démontrer que pour tout $n\in \mathbb {N} ,f_{n}'=-f_{n+1}$ . Puisque ${\frac {\mathrm {d} }{\mathrm {d} x}}\left({\frac {\ln ^{n}(k)}{k^{x}}}\right)=-{\frac {\ln ^{n+1}(k)}{k^{x}}}$ , le problème est d'intervertir ${\frac {\mathrm {d} }{\mathrm {d} x}}$ et $\sum _{k=1}^{\infty }$ .

Remarquons d'abord que toutes les fonctions $f_{n}$ sont continues car localement lipschitziennes. En effet, pour tout $c>1$ , on a, d'après le théorème des accroissements finis et par décroissance de $x\mapsto {\frac {\ln(k)}{k^{x}}}$ :

\forall a,b\in \left[c,+\infty \right[\quad \forall k\geq 1\quad \left|{\frac {1}{k^{b}}}-{\frac {1}{k^{a}}}\right|\leq |b-a|{\frac {\ln(k)}{k^{c}}}

donc

\forall a,b\in \left[c,+\infty \right[\quad \left|f_{n}(b)-f_{n}(a)\right|\leq |b-a|f_{n+1}(c)

.

Par les mêmes arguments, pour tous $a,b>1$ on a $-f_{n+1}(\min(a,b))\leq {\frac {f_{n}(b)-f_{n}(a)}{b-a}}\leq -f_{n+1}(\max(a,b))$ . En faisant tendre $b$ vers $a$ et en utilisant la continuité de $f_{n+1}$ , on en déduit le résultat souhaité :

\forall a\in \left]1,+\infty \right[\quad f_{n}'(a)=-f_{n+1}(a)

.

Sens de variation

La fonction zêta est décroissante, puisque sa dérivée $x\mapsto -\sum _{k=1}^{\infty }{\frac {\ln(k)}{k^{x}}}$ est négative.

Limite au bornes de domaine de définition

Nous utiliserons le lemme suivant :

Lemme

$\forall x\in \left]1,+\infty \right[\qquad 1+{\frac {1}{(x-1)2^{x-1}}}\leqslant \zeta (x)\leqslant 1+{\frac {1}{x-1}}$ .

Démonstration

Soit $x\in \left]1,+\infty \right[$ .

Pour tout $k\in \mathbb {N} ^{*}$ , on a :

\forall t\in \left[k,k+1\right]\quad k^{x}\leqslant t^{x}\leqslant (k+1)^{x}{\text{ donc }}{\frac {1}{(k+1)^{x}}}\leqslant {\frac {1}{t^{x}}}\leqslant {\frac {1}{k^{x}}}

donc

\int _{k}^{k+1}{\frac {1}{(k+1)^{x}}}\,\mathrm {d} t\leqslant \int _{k}^{k+1}{\frac {1}{t^{x}}}\,\mathrm {d} t\leqslant \int _{k}^{k+1}{\frac {1}{k^{x}}}\,\mathrm {d} t

,

c'est-à-dire

{\frac {1}{(k+1)^{x}}}\leqslant \int _{k}^{k+1}{\frac {1}{t^{x}}}\,\mathrm {d} t\leqslant {\frac {1}{k^{x}}}

.

Par conséquent :

\forall k\geq 2\quad \int _{k}^{k+1}{\frac {1}{t^{x}}}\,\mathrm {d} t\leqslant {\frac {1}{k^{x}}}\leqslant \int _{k-1}^{k}{\frac {1}{t^{x}}}\,\mathrm {d} t

.

En sommant, on a donc l'encadrement :

\int _{2}^{+\infty }{\frac {1}{t^{x}}}\,\mathrm {d} t\leqslant \sum _{k=2}^{+\infty }{\frac {1}{k^{x}}}\leqslant \int _{1}^{+\infty }{\frac {1}{t^{x}}}\,\mathrm {d} t

,

qui nous donne :

{\frac {1}{(x-1)2^{x-1}}}\leqslant \zeta (x)-1\leqslant {\frac {1}{x-1}}

et finalement :

1+{\frac {1}{(x-1)2^{x-1}}}\leqslant \zeta (x)\leqslant 1+{\frac {1}{x-1}}

.

Grâce au théorème des gendarmes, on déduit du lemme :

$\lim _{x\to 1}\zeta (x)=+\infty$ ;
$\lim _{x\to +\infty }\zeta (x)=1$ .

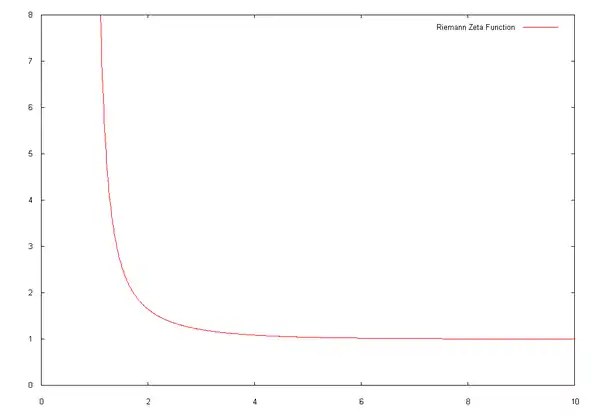
Tracé de la fonction

Compte tenu des renseignements précédents, nous pouvons en déduire le tracé de la fonction zêta qui est le suivant :

Développements asymptotiques de la fonction zêta

Nous commencerons par étudier le comportement de la fonction zêta au voisinage de 1 :

Propriété

$\zeta (x)\sim _{x\to 1^{+}}{\frac {1}{x-1}}$ .

Démonstration

Reprenons l'encadrement du lemme précédent :

\forall x\in \left]1,+\infty \right[\qquad 1+{\frac {1}{(x-1)2^{x-1}}}\leqslant \zeta (x)\leqslant 1+{\frac {1}{x-1}}

.

On en déduit :

\forall x\in \left]1,+\infty \right[\qquad x-1+{\frac {1}{2^{x-1}}}\leqslant (x-1)\zeta (x)\leqslant x

puis, d’après le théorème de l'encadrement :

\lim _{x\to 1^{+}}(x-1)\zeta (x)=1

,

ce qui conclut.

Remarque

On montre et nous admettrons que :

\lim _{x\to 1^{+}}\left(\zeta (x)-{\frac {1}{x-1}}\right)=\gamma

,

$γ$ étant la constante d'Euler.

En 1, on a donc le développement asymptotique suivant :

\zeta (x)={\frac {1}{x-1}}+\gamma +o(1)

.

Nous étudierons ensuite le comportement de la fonction zêta au voisinage de l'infini :

Propriété

En $+\infty$ , on a :

\zeta (x)=1+{\frac {1}{2^{x}}}+o\left({\frac {1}{2^{x}}}\right)

.

Démonstration

\zeta (x)-1-{\frac {1}{2^{x}}}=\sum _{k=3}^{\infty }{\frac {1}{k^{x}}}>0

et

\sum _{k=3}^{\infty }{\frac {1}{k^{x}}}=\sum _{k=2}^{\infty }{\frac {1}{(k+1)^{x}}}\leq \sum _{k=2}^{\infty }{\frac {1}{(2{\sqrt {k}})^{x}}}={\frac {1}{2^{x}}}\left(\zeta (x/2)-1\right)

.

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.