Moment d'inertie

Lequel de ces mouvements est le plus difficile ?

Le moment d'inertie est au mouvement de rotation l'analogue de la masse pour le mouvement de translation : il reflète la « résistance » qu'oppose un corps à sa mise en mouvement.

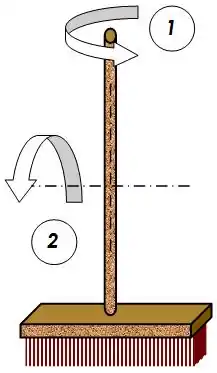
Cette difficulté est d'autant plus grande, dans le cas de la rotation d'un solide, que les masses en son sein se trouvent loin de l'axe de rotation. Ainsi par exemple dans le cas d'un balai pris en main au milieu du manche (cf. figure ci-contre), il est plus aisé de le faire tourner autour de l'axe du manche (cas 1), qu'autour de l'axe transversal indiqué (cas 2). En effet, dans ce dernier cas la brosse, dont la masse relative par rapport au manche est importante, est située plus loin de l'axe de rotation que dans le premier cas (il y a également dissymétrie dans la répartition des masses autour de l'axe de rotation). Comme pour un solide en rotation, la vitesse linéaire d'un point croît en proportion avec cet éloignement, il est nécessaire, à vitesse angulaire égale, de communiquer une plus grande énergie cinétique aux points éloignés. D'où la plus grande résistance du balai à tourner autour d'un axe transversal qu'autour de l'axe du manche.

Dans cette analogie, l'énergie nécessaire à la mise en mouvement se transforme (d'une manière ou d'une autre) en énergie cinétique. Dans le cas d'un mouvement de translation, l'énergie cinétique d'un point de masse m est donnée par la formule ${\displaystyle E_{k}={\frac {1}{2}}mv^{2}}$. Dans le cas d'une rotation d'un solide autour d'un axe fixe, il est possible de montrer que l'énergie cinétique totale se met sous la forme ${\displaystyle E_{k}={\frac {1}{2}}J_{\Delta }\,\omega ^{2}}$, où le terme ${\displaystyle J_{\Delta }}$ est précisément le moment d'inertie par rapport à l'axe de rotation, c'est-à-dire une forme analogue à celle de l'énergie cinétique du mouvement de translation. Le moment d'inertie apparaît ainsi comme l'analogue de la masse (inerte) du solide dans le cas du mouvement de translation, et est donc en relation avec la "résistance" de celui-ci à sa mise "en rotation". En fait l'explication du phénomène empirique de plus grande "résistance à tourner" du balai selon que le choix de l'axe de rotation axial ou transversal est liée au fait que le moment d'inertie par rapport à l'axe dans ce dernier cas est plus grand que dans le premier.

L'énergie cinétique étant une grandeur extensive, c'est-à-dire que sa valeur sur un système complexe est la somme des valeurs sur les parties élémentaires, l'énergie cinétique totale du solide considéré s'exprime donc sous la forme :

${\displaystyle E_{k}=\sum _{i}{\tfrac {1}{2}}m_{i}v_{i}^{2}=\sum _{i}{\tfrac {1}{2}}m_{i}(\omega r_{i})^{2}={\tfrac {1}{2}}\omega ^{2}\sum _{i}m_{i}r_{i}^{2}\ {\overset {\mathrm {def} }{=}}\ {\tfrac {1}{2}}J_{\Delta }.\omega ^{2}}$,

avec :

• ${\displaystyle r_{i}=\mathrm {H} _{i}\mathrm {M} _{i}}$, distance du point ${\displaystyle \mathrm {M} _{i}}$ à l'axe de rotation ${\displaystyle \Delta }$ (${\displaystyle \mathrm {H} _{i}}$ désignant la projection de ${\displaystyle \mathrm {M} _{i}}$ sur ${\displaystyle \Delta }$) ;
• ${\displaystyle J_{\Delta }=\sum _{i}m_{i}r_{i}^{2}}$.

Cette expression possède une analogie évidente avec celle de l'énergie cinétique pour un point matériel (ou un solide en translation), où celle-ci s'écrit ${\displaystyle E_{k}={\tfrac {1}{2}}mv^{2}}$. Dans le cas de la rotation la vitesse angulaire ω est l'homologue de la vitesse linéaire v, et le moment d'inertie ${\displaystyle J_{\Delta }}$ comme l'homologue de la masse m. Toutefois le moment d'inertie dépend également de la répartition des masses autour de l'axe ${\displaystyle \Delta }$ et sa valeur dépend donc du choix de celui-ci.

En tant qu'homologue de la masse (inerte) pour la rotation, ce terme reflète la "résistance" du solide à sa mise en rotation, comme il avait été indiqué dans l'approche empirique précédente.

De la même façon que pour l'énergie cinétique, et du fait du caractère extensif de cette grandeur, le moment cinétique du solide par rapport à un point quelconque ${\displaystyle \mathrm {O} }$ de l'axe s'exprime alors sous la forme, en utilisant les mêmes notations que précédemment :

${\displaystyle {\vec {L}}_{\mathrm {O} }=\sum _{i}m_{i}{\overrightarrow {\mathrm {OM} _{i}}}\wedge {\vec {v}}_{i}=\sum _{i}m_{i}({\overrightarrow {\mathrm {OH} _{i}}}+{\vec {r}}_{i})\wedge {\vec {v}}_{i}}$

Comme la vitesse d'un point ${\displaystyle \mathrm {M} _{i}}$ est donnée par ${\displaystyle {\vec {v}}_{i}={\vec {\omega }}\wedge {\vec {r}}_{i}}$, la composante du moment cinétique colinéaire à l'axe de rotation ${\displaystyle \Delta }$ correspond au second terme de la somme[1], et se met sous la forme :

${\displaystyle {\vec {L}}_{\Delta }=\sum _{i}m_{i}{\vec {r}}_{i}\wedge {\vec {v}}_{i}=\sum _{i}m_{i}{\vec {r}}_{i}\wedge \left({\vec {\omega }}\wedge {\vec {r}}_{i}\right)=\sum _{i}m_{i}\left(r_{i}^{2}{\vec {\omega }}-({\vec {\omega }}\cdot {\vec {r}}_{i}){\vec {r}}_{i}\right)=\left(\sum _{i}m_{i}r_{i}^{2}\right){\vec {\omega }}=J_{\Delta }{\vec {\omega }}}$, puisque ${\displaystyle {\vec {\omega }}\cdot {\vec {r}}_{i}=0}$ par hypothèse.

Dans les deux cas apparaît la grandeur caractéristique, qui ne dépend que de la géométrie des masses du solide, appelé moment d'inertie ${\displaystyle J_{\Delta }}$ par rapport à l'axe ${\displaystyle \Delta }$ :

${\displaystyle J_{\Delta }=\sum _{i}m_{i}r_{i}^{2}}$.

Remarque : il convient de souligner que ${\displaystyle {\vec {L}}_{\mathrm {O} }}$, moment cinétique du solide au point ${\displaystyle \mathrm {O} }$ de l'axe de rotation n'est pas en général colinéaire à cet axe. Ce n'est que si l'axe de rotation coïncide avec un axe principal d'inertie du solide, ce qui est notamment le cas s'il est un axe de symétrie matérielle du solide, c'est-à-dire à la fois axe de symétrie géométrique et que pour tout couple de points ${\displaystyle (\mathrm {M} _{i},\mathrm {M} _{j})}$ symétriques l'un par rapport à l'autre on ait ${\displaystyle m_{i}=m_{j}}$, que ${\displaystyle {\vec {L}}_{\mathrm {O} }}$ sera colinéaire à l'axe de rotation. En fait on aura alors ${\displaystyle {\vec {L}}_{\mathrm {O} }=J_{\Delta }{\vec {\omega }}}$ par rapport à tout point ${\displaystyle \mathrm {O} }$ situé sur l'axe de rotation.

Du fait de sa définition , le moment d'inertie a les dimensions d'une masse par le carré d'une longueur soit M·L². Son unité dans le système international d'unités pourra donc naturellement être exprimée en kg⋅m², unité qui n'a pas de nom propre.

On peut cependant remarquer que dans la relation ${\displaystyle E={\frac {1}{2}}J_{\Delta }.\omega ^{2}}$, la vitesse de rotation ω n'est pas exprimée en s⁻¹, mais en rad⋅s⁻¹. Toutefois, étant défini comme le rapport de deux longueurs, le radian, considéré comme unité dérivée du système international depuis la 20^e conférence générale du BIPM[2], est sans dimension, par suite ceci n'affecte pas l'homogénéité de l'équation aux dimensions de l'expression de l'énergie cinétique. Il ne serait cependant pas faux que le moment d'inertie soit exprimé en kg⋅m²⋅rad⁻², mais ce choix est rarement retenu en pratique. Son seul intérêt serait de rappeler qu'il s'agit d'une unité spécifiquement rattachée au mouvement de rotation, comme pour toutes les unités où le radian apparaît.

Par extension dans un solide considéré comme un ensemble continu de points matériels ${\displaystyle x}$ affectés d'une masse volumique ${\displaystyle \rho }$, le moment d'inertie s'écrit :

${\displaystyle J_{\Delta }\ {\overset {\mathrm {def} }{=}}\ \iiint d(x,\Delta )^{2}\;\mathrm {d} m=\iiint d(x,\Delta )^{2}\,\rho \;\mathrm {d} V}$

où

• ${\displaystyle d(x,\Delta )}$ est la distance entre le point ${\displaystyle x}$ et l'axe Δ ;
• ${\displaystyle \mathrm {d} V}$ est un volume élémentaire autour de ${\displaystyle x}$ ;
• ${\displaystyle \mathrm {d} m}$ est la masse de ce volume élémentaire ;
• ${\displaystyle \rho }$ est la masse volumique autour de ${\displaystyle x}$.

Cette définition peut également prendre une forme vectorielle :

${\displaystyle J_{\Delta }\ {\overset {\mathrm {def} }{=}}\ \iiint {\bigl \|}{\vec {e}}_{\Delta }\wedge {\overrightarrow {\mathrm {OM} }}{\bigr \|}^{2}\mathrm {d} m=\iiint {\bigl \|}{\vec {e}}_{\Delta }\wedge {\overrightarrow {\mathrm {OM} }}{\bigr \|}^{2}\,\rho \;\mathrm {d} V}$

où

• ${\displaystyle \mathrm {O} }$ est un point sur l'axe ${\displaystyle \Delta }$ ;
• ${\displaystyle \mathrm {M} }$ est un point du solide considéré ;
• ${\displaystyle {\vec {e}}_{\Delta }}$ est un vecteur unitaire de l'axe ${\displaystyle \Delta }$ ;
• ${\displaystyle \wedge }$ désigne le produit vectoriel et ${\displaystyle \|\,\|}$ la norme euclidienne.

En toute rigueur, la notion de moment d'inertie n'est définie que si la quantité ${\displaystyle \sum _{i}m_{i}r_{i}^{2}}$ peut être isolée des expressions de l'énergie cinétique ou du moment cinétique de rotation, c'est-à-dire que dans la mesure où la vitesse angulaire est la même pour les points du système à un instant donné. Ceci n'est valable strictement que dans le cas du modèle du solide indéformable.

Toutefois, la définition précédente peut s'étendre à un système déformable, dès lors qu'il ne présente pas de rotation différentielle, ou que l'on peut négliger l'effet de celle-ci, de façon qu'il soit possible de considérer que tous les points du système ont à un instant donné la même vitesse angulaire. Par exemple un système articulé, constitué de plusieurs solides reliés entre eux par des liaisons, en rotation autour d'un axe fixe, si les vitesses angulaires de rotation entre les diverses parties sont petites devant la vitesse angulaire de rotation « globale ». Toutefois, pour un système déformable le moment d'inertie n'est plus constant dans le temps.

Dans la comparaison entre le mouvement de rotation et le mouvement de translation, le moment cinétique est l'homologue de la quantité de mouvement, et pour un système isolé est une grandeur conservative.

Comme indiqué précédemment, il découle de la définition du moment d'inertie que plus les masses constituant un solide sont réparties loin de l'axe de rotation, plus son moment d'inertie par rapport à cet axe est important. Comme la composante axiale du moment cinétique est égale au moment d'inertie multiplié par sa vitesse angulaire de rotation, et du fait de son caractère conservatif, si le moment d'inertie d'un système diminue du fait d'une variation de sa géométrie interne, sa vitesse angulaire de rotation doit augmenter (et inversement).

Ainsi, le patineur sur glace[3] rapproche les bras de son corps lors d'une pirouette. Cela a pour effet de diminuer son moment d'inertie, ce qui, par conservation du moment cinétique[4], implique une plus grande vitesse de rotation.

De même, les enfants jouant à mettre en rotation un tourniquet en courant à ses côtés atteignent une vitesse de rotation limitée par leur course. Ils peuvent cependant ensuite sauter sur le tourniquet en mouvement, puis se positionner en son centre, augmentant ainsi significativement la vitesse de rotation initialement obtenue.

Le moment cinétique propre ${\displaystyle {\vec {L}}^{*}}$ d'un solide de vecteur rotation instantané ${\displaystyle {\vec {\omega }}(t)}$ s'écrit :

${\displaystyle {\vec {L}}^{*}=\sum _{i}m_{i}{\vec {r}}_{i}\wedge {\vec {v}}_{i}^{*}=\sum _{i}m_{i}{\vec {r}}_{i}\wedge \left({\vec {\omega }}\wedge {\vec {r}}_{i}\right)=\sum _{i}m_{i}\left(r_{i}^{2}{\vec {\omega }}-\left({\vec {\omega }}\cdot {\vec {r}}_{i}\right){\vec {r}}_{i}\right)}$,

Il est possible d'exprimer par exemple la composante suivant x en coordonnées cartésiennes, ce qui donne :

${\displaystyle L_{x}^{*}=\sum _{i}m_{i}r_{i}^{2}\omega _{x}-\sum _{i}m_{i}\left(x_{i}\omega _{x}+y_{i}\omega _{y}+z_{i}\omega _{z}\right)x_{i}=\left(\sum _{i}m_{i}\left(y_{i}^{2}+z_{i}^{2}\right)\right)\omega _{x}-\left(\sum _{i}m_{i}x_{i}y_{i}\right)\omega _{y}-\left(\sum _{i}m_{i}x_{i}z_{i}\right)\omega _{z}}$.

Dans cette expression, les facteurs entre parenthèses représentent respectivement le moment d'inertie du solide par rapport à l'axe Ox, noté ${\displaystyle I_{\mathrm {O} x}}$, et deux termes homogènes à un moment d'inertie, appelés produits d'inertie, notés ${\displaystyle I_{xy}}$ et ${\displaystyle I_{xz}}$. Il est possible d'écrire ${\displaystyle L_{x}}$ sous la forme :

${\displaystyle L_{x}={\begin{bmatrix}I_{\mathrm {O} x}&-I_{xy}&-I_{xz}\end{bmatrix}}{\vec {\omega }}}$,

et en procédant de même pour les autres composantes il vient finalement l'expression du moment cinétique propre sous la forme :

${\displaystyle {\vec {L}}^{*}={\bar {\bar {I}}}{\vec {\omega }}}$,

avec ${\displaystyle {\bar {\bar {I}}}}$ tenseur (ou opérateur) d'inertie, qui est défini par :

${\displaystyle {\bar {\bar {I}}}={\begin{bmatrix}I_{\mathrm {O} x}&-I_{xy}&-I_{xz}\\-I_{xy}&I_{\mathrm {O} y}&-I_{yz}\\-I_{xz}&-I_{yz}&I_{\mathrm {O} z}\end{bmatrix}}={\begin{bmatrix}\sum _{i}m_{i}(y_{i}^{2}+z_{i}^{2})&-\sum _{i}m_{i}x_{i}y_{i}&-\sum _{i}m_{i}x_{i}z_{i}\\-\sum _{i}m_{i}x_{i}y_{i}&\sum _{i}m_{i}(x_{i}^{2}+z_{i}^{2})&-\sum _{i}m_{i}y_{i}z_{i}\\-\sum _{i}m_{i}x_{i}z_{i}&-\sum _{i}m_{i}y_{i}z_{i}&\sum _{i}m_{i}(x_{i}^{2}+y_{i}^{2})\end{bmatrix}}}$,

expression dans laquelle les éléments diagonaux sont les moments d'inertie du solide par rapport aux divers axes, et les éléments non diagonaux sont les produits d'inertie. De même, l'énergie cinétique propre s'écrit : ${\displaystyle E_{c}^{*}={\tfrac {1}{2}}{\vec {\omega }}\cdot ({\bar {\bar {I}}}{\vec {\omega }})}$.

Il est clair que ${\displaystyle {\bar {\bar {I}}}}$ ne dépend que de la géométrie des masses du solide. Il découle des relations précédentes que dans le cas général le moment cinétique propre du système n'est pas colinéaire à l'axe instantané de rotation, les relations précédentes généralisant celles obtenues dans le cas de la rotation autour d'un axe fixe[7].

Le moment d'inertie par rapport à un axe quelconque, de direction donnée par le vecteur unitaire ${\displaystyle {\vec {n}}}$ est alors donné par ${\displaystyle I={\vec {n}}\cdot ({\bar {\bar {I}}}{\vec {n}})}$.

Il est facile de montrer que ${\displaystyle {\bar {\bar {I}}}}$ est effectivement un tenseur. En effet, en adoptant la notation ${\displaystyle x_{i,1}=x_{i},x_{i,2}=y_{i},x_{i,3}=z_{i}}$ il est possible de remarquer que la composante ${\displaystyle I_{\alpha \beta }}$ de ${\displaystyle {\bar {\bar {I}}}}$ se met sous la forme suivante[8] :

${\displaystyle I_{\alpha \beta }=\left(\sum _{i}m_{i}r_{i}^{2}\right)\delta _{\alpha \beta }-\sum _{i}m_{i}x_{i,\alpha }x_{i,\beta }}$.

Le premier terme est le produit d'un scalaire (le moment d'inertie par rapport au point O, ${\displaystyle \sum _{i}m_{i}r_{i}^{2}}$) par un tenseur (le tenseur de Kronecker ${\displaystyle \delta _{ij}}$). Le second terme correspond à une somme dans lequel chaque terme correspond au produit d'un scalaire (la masse m_i) par ${\displaystyle T_{i,\alpha \beta }=x_{i,\alpha }x_{i,\beta }}$. Or il s'agit là des composantes du tenseur résultant du produit tensoriel du vecteur ${\displaystyle {\vec {r}}_{i}}$ par lui-même, donc celles d'un tenseur. Par suite ${\displaystyle {\bar {\bar {I}}}}$ est donc bien un tenseur d'ordre deux[9] : ceci était nécessaire de façon à assurer le caractère invariant par changement du système de coordonnées des expressions précédentes de ${\displaystyle {\vec {L}}^{*}}$ et ${\displaystyle E_{c}^{*}}$. Ce tenseur est évidemment symétrique.

Du fait de son caractère symétrique il est toujours possible de choisir un système d'axe tel que la matrice représentant ${\displaystyle {\bar {\bar {I}}}}$ soit diagonale[10]. De tels axes sont dits axes principaux d'inertie. Les moments d'inertie correspondants sont appelés moments principaux d'inertie, et sont notés ${\displaystyle I_{1},I_{2},I_{3}}$. Leurs valeurs dépendent de la forme géométrique du solide et de la distribution de la masse en son sein, donc de l'expression que prend sa masse volumique ${\displaystyle \rho ({\vec {r}})}$ en chaque point du solide. Pour un solide homogène ρ est constante, et les moments principaux d'inertie ne dépendent alors que de la forme géométrique du solide.

En général un solide quelconque possède trois moments principaux d'inertie différents, il est appelé toupie asymétrique[11]. Si deux moments principaux d'inertie sont égaux, par exemple ${\displaystyle I_{1}=I_{2}\neq I_{3}}$, le corps est qualifié de toupie symétrique, et si tous les moments principaux sont égaux, de toupie sphérique. Par exemple un parallélépipède homogène quelconque sera une toupie asymétrique, un cône ou un cylindre homogène une toupie symétrique et une sphère homogène une toupie sphérique. La Terre, du fait de son aplatissement aux pôles, est également en général considérée comme une toupie symétrique.

La présence d'éléments de symétrie matérielle simplifie grandement la recherche des axes principaux d'inertie. En effet en présence de tels éléments certains produits d'inertie, par nature impairs par réflexions, s'annulent, ce qui permet de diagonaliser facilement la matrice représentant ${\displaystyle {\bar {\bar {I}}}}$.

Un élément de symétrie (point, axe, plan) matérielle est non seulement un élément par rapport auquel le solide est géométriquement symétrique, mais aussi pour lequel sa masse volumique présente la même symétrie. Ainsi un cylindre homogène comporte-t-il un axe de symétrie matérielle (son axe), par lequel passe une infinité de plans de symétrie matérielle, ainsi qu'un autre plan de symétrie matérielle qui est celui perpendiculaire à son axe passant par le milieu du cylindre. En revanche, si le cylindre est constitué de deux demi-cylindres tous deux homogènes, mais de masses volumiques différentes, accolés dans un plan contenant leurs axes, le cylindre possède toujours le plan de symétrie matérielle précédent, mais son axe n'est plus axe de symétrie matérielle. En revanche le plan de symétrie commun des deux demi-cylindres est toujours plan de symétrie matérielle du système.

Il est possible de montrer compte tenu des expressions précédentes des produits d'inertie les propriétés suivantes[12] :

• Tout axe de symétrie matérielle est axe principal d'inertie;
• Tout axe perpendiculaire à un plan de symétrie matérielle est axe principal d'inertie;

Ainsi un cylindre homogène a pour axes principaux d'inertie son axe ainsi que tout axe qui y est perpendiculaire, passant par son centre. Par suite, deux des moments principaux d'inertie sont égaux et le tenseur d'inertie prend dans cette base la forme suivante :

${\displaystyle {\bar {\bar {I}}}={\begin{bmatrix}I_{1}&0&0\\0&I_{1}&0\\0&0&I_{3}\end{bmatrix}}}$. Il s'agit donc d'une toupie symétrique.

Le potentiel de gravitation créé par une distribution quelconque de points matériels ${\displaystyle M_{i}}$ de masses ${\displaystyle m_{i}}$ ne se ramène pas en général à la forme obtenue dans le cas d'une distribution de masse à symétrie sphérique. Toutefois la plupart des corps célestes (étoile, planètes…) possède approximativement cette symétrie et les écarts à la sphéricité demeurent faibles. Ces écarts sont évidemment liés à la répartition de la matière au sein de la distribution de masse, et donc doivent être (au moins pour les premières corrections) en relation avec le tenseur d'inertie de la distribution (assimilée à un solide parfait dans la suite) : de fait il est possible de montrer facilement que la première correction non nulle au potentiel sphérique fait intervenir une grandeur tensorielle, le tenseur de moment quadrupolaire de la distribution de masse, dont les composantes s'expriment de façon simple en fonction de celles du tenseur d'inertie.

De façon générale à grande distance d'une distribution de masse le potentiel créé peut se mettre sous la forme d'un développement multipolaire : chaque point matériel constituant la distribution (de masse totale ${\displaystyle \sum _{i}m_{i}=M}$), repéré par le vecteur ${\displaystyle {\vec {r}}_{i}={\overrightarrow {OM_{i}}}}$ par rapport à une origine O génère en ${\displaystyle {\vec {r}}={\overrightarrow {OM}}}$ le potentiel

${\displaystyle \phi _{i}({\vec {r}})=-{\frac {Gm_{i}}{r}}\sum _{k=0}^{\infty }\left({\frac {r_{i}}{r}}\right)^{k}P_{k}(\cos \theta _{i})}$,

dans lequel ${\displaystyle \theta _{i}}$ est l'angle entre ${\displaystyle {\vec {r}}}$ et ${\displaystyle {\vec {r}}_{i}}$ et ${\displaystyle P_{k}(z)}$ est le polynôme de Legendre d'ordre k.

Comme r>>r_i il est possible de se limiter aux 3 premier termes, ce qui donne :

${\displaystyle \phi _{i}({\vec {r}})\approx -{\frac {Gm_{i}}{r}}\left(1+{\frac {r_{i}\cos \theta _{i}}{r}}+{\frac {r_{i}^{2}(3\cos ^{2}\theta _{i}-1)}{2r^{2}}}\right)}$,

ce qui compte tenu de ${\displaystyle \cos \theta _{i}={\frac {{\vec {r}}_{i}\cdot {\vec {r}}}{rr_{i}}}}$ devient :

${\displaystyle \phi _{i}({\vec {r}})\approx -{\frac {Gm_{i}}{r}}\left(1+{\frac {{\vec {r}}\cdot {\vec {r}}_{i}}{r^{2}}}+{\frac {(3({\vec {r}}\cdot {\vec {r}}_{i})^{2}-r^{2}r_{i}^{2})}{2r^{4}}}\right)}$.

Le potentiel créé par la distribution en M est égale à la somme des potentiels ${\displaystyle \phi _{i}({\vec {r}})}$, et chacun des trois termes se met alors sous la forme :

• terme d'ordre 0 ou polaire : ${\displaystyle \Phi ^{(0)}({\vec {r}})=-{\frac {GM}{r}}}$. C'est le potentiel à symétrie sphérique créé par une masse ponctuelle M à l'origine O ;
• terme d'ordre 1 ou dipolaire : ${\displaystyle \Phi ^{(1)}({\vec {r}})=-{\frac {G{\vec {r}}}{r^{3}}}\cdot (\sum _{i}m_{i}{\vec {r}}_{i})}$, or en prenant pour origine le centre de masse du système, ${\displaystyle \sum _{i}m_{i}{\vec {r}}_{i}={\vec {0}}}$, et le terme dipolaire est nul[13] ;
• terme d'ordre 2 ou quadrupolaire : ${\displaystyle \Phi ^{(2)}({\vec {r}})=-{\frac {G}{2r^{5}}}\sum _{i}m_{i}\left[3\left({\vec {r}}\cdot {\vec {r}}_{i}\right)^{2}-r^{2}r_{i}^{2}\right]}$.

Ce dernier terme est donc la première correction, a priori non nulle, traduisant la non-sphéricité à grande distance du potentiel de gravitation créé par une distribution de masse. La somme sur i qui apparaît dans celui-ci peut être réécrite sous la forme :

${\displaystyle \sum _{i}m_{i}\left[3\left({\vec {r}}\cdot {\vec {r}}_{i}\right)^{2}-r^{2}r_{i}^{2}\right]={\vec {r}}\cdot ({\bar {\bar {Q}}}{\vec {r}})}$,

où ${\displaystyle {\bar {\bar {Q}}}}$ est le moment quadrupolaire de la distribution de masse :

${\displaystyle {\bar {\bar {Q}}}={\begin{bmatrix}3\sum _{i}m_{i}x_{i}^{2}-\sum _{i}m_{i}r_{i}^{2}&3\sum _{i}m_{i}x_{i}y_{i}&3\sum _{i}m_{i}x_{i}z_{i}\\3\sum _{i}m_{i}x_{i}y_{i}&3\sum _{i}m_{i}y_{i}^{2}-\sum _{i}m_{i}r_{i}^{2}&3\sum _{i}m_{i}y_{i}z_{i}\\3\sum _{i}m_{i}x_{i}z_{i}&3\sum _{i}m_{i}y_{i}z_{i}&3\sum _{i}m_{i}z_{i}^{2}-\sum _{i}m_{i}r_{i}^{2}\end{bmatrix}}}$,

Chaque composante de ce tenseur se met donc sous la forme : ${\displaystyle Q_{\alpha \beta }=3\sum _{i}m_{i}x_{i,\alpha }x_{i,\beta }-\delta _{\alpha \beta }\sum _{i}m_{i}r_{i}^{2}}$, et compte tenu de l'expression générale des composantes du tenseur d'inertie d'un solide ${\displaystyle I_{\alpha \beta }=\left(\sum _{i}m_{i}r_{i}^{2}\right)\delta _{\alpha \beta }-\sum _{i}m_{i}x_{i,\alpha }x_{i,\beta }}$ il vient finalement l'expression générale[14] : ${\displaystyle Q_{\alpha \beta }=\mathrm {Tr} ({\bar {\bar {I}}})\delta _{\alpha \beta }-3I_{\alpha \beta }}$,

où ${\displaystyle \mathrm {Tr} ({\bar {\bar {I}}})}$ désigne la trace de la matrice représentant le tenseur d'inertie, c'est-à-dire la somme de ses termes diagonaux[15].

Les axes principaux d'inertie, pour lesquels la matrice représentant ${\displaystyle {\bar {\bar {I}}}}$ est diagonale, constituent également une base dans lequel ${\displaystyle {\bar {\bar {Q}}}}$ est également diagonale, il vient pour les composantes de ce dernier l'expression ${\displaystyle Q_{\alpha }=(I_{1}+I_{2}+I_{3})-3I_{\alpha }}$.

Dans le cas où la distribution de masse est à symétrie sphérique tous les moments principaux d'inertie sont égaux, et alors ${\displaystyle {\bar {\bar {Q}}}=0}$. Ce résultat est physiquement évident, et en fait dans ce cas tous les termes d'ordre supérieur du développement multipolaire précédent sont également nuls.

Une planète comme la Terre se comporte comme une toupie symétrique pour laquelle ${\displaystyle I_{1}=I_{2}<I_{3}}$[16], l'axe principal d'inertie selon Oz correspondant pratiquement à son axe de rotation. Dans ce cas d'après les formules précédentes le potentiel gravitationnel à grande distance se met sous la forme :

${\displaystyle \Phi ({\vec {r}})\approx {\frac {-Gm}{r}}+{\frac {GM_{T}(I_{3}-I_{1})}{r^{3}}}\left[3\cos ^{2}\theta -1\right]}$, où ${\displaystyle \theta }$ est l'angle entre la direction de ${\displaystyle {\vec {r}}}$ et celle de l'axe principal d'inertie Oz.

Le moment d'inertie d'un solide quelconque de tenseur d'inertie ${\displaystyle {\bar {\bar {I}}}}$ par rapport à un axe quelconque dont la direction est donnée par le vecteur unitaire ${\displaystyle {\vec {n}}}$ est donné par :

${\displaystyle I={\vec {n}}\cdot ({\bar {\bar {I}}}{\vec {n}})}$,

en posant ${\displaystyle {\vec {\rho }}={\frac {\vec {n}}{\sqrt {I}}}}$ cette relation peut se mettre sous la forme :

${\displaystyle {\vec {\rho }}\cdot ({\bar {\bar {I}}}{\vec {\rho }})=1}$,

en explicitant avec les composantes ${\displaystyle (\rho _{x},\rho _{y},\rho _{z})}$ de ce vecteur, il vient l'équation d'un ellipsoïde :

${\displaystyle I_{\mathrm {O} x}\rho _{1}^{2}+I_{\mathrm {O} y}\rho _{2}^{2}+I_{\mathrm {O} z}\rho _{3}^{2}+2I_{xy}\rho _{1}\rho _{2}+2I_{xz}\rho _{1}\rho _{3}+2I_{yz}\rho _{2}\rho _{3}=1}$,

laquelle prend dans les axes principaux d'inertie une forme particulièrement simple :

${\displaystyle I_{1}\rho _{1}^{2}+I_{2}\rho _{2}^{2}+I_{3}\rho _{3}^{2}=1}$.

Cet ellipsoïde est appelé ellipsoïde d'inertie[17]. Dans le cas d'une toupie symétrique, il s'agit d'un ellipsoïde de révolution, et dans le cas d'une toupie sphérique, d'une sphère. Cette notion n'a plus en général aujourd'hui qu'un intérêt historique, toutefois il est intéressant de remarquer que les axes principaux d'inertie sont les axes principaux de l'ellipsoïde d'inertie.

Pour une boule homogène de rayon ${\displaystyle R}$ et de centre ${\displaystyle O}$, les moments d'inertie au centre de la boule par rapport aux trois axes sont égaux. On peut donc écrire :

${\displaystyle J_{\Delta }={\frac {1}{3}}(J_{\mathrm {O} x}+J_{\mathrm {O} y}+J_{\mathrm {O} z})={\frac {1}{3}}\int _{V}[(y^{2}+z^{2})+(z^{2}+x^{2})+(x^{2}+y^{2})]\,\mathrm {d} m={\frac {2}{3}}\int _{V}(x^{2}+y^{2}+z^{2})\,\mathrm {d} m={\frac {2}{3}}\int _{V}r^{2}\,\mathrm {d} m}$

En désignant par ${\displaystyle \rho }$ la masse volumique, ${\displaystyle \mathrm {d} m=\rho \,4\pi r^{2}\mathrm {d} r}$ donc :

${\displaystyle J_{\Delta }={\frac {2}{3}}\int _{0}^{R}r^{2}(\rho \,4\pi r^{2}\mathrm {d} r)={\frac {8}{15}}\pi R^{5}\rho }$

Comme la masse de la boule est ${\displaystyle M={\frac {4}{3}}\pi R^{3}\rho }$, on obtient[18] :

${\displaystyle J_{\Delta }={\frac {2}{5}}M\,R^{2}}$.

Pour une sphère (par parenthèses une sphère est une surface, donc creuse), comme pour une boule, les moments d'inertie passant par son centre sont égaux. En l'occurrence, si son rayon est ${\displaystyle R}$, on a[19] :

${\displaystyle J_{\Delta }={\frac {2}{3}}MR^{2}}$

Dans le cas d'une barre de section négligeable et de longueur ${\displaystyle L}$, le moment d'inertie selon un axe perpendiculaire à la barre est, en son centre :

${\displaystyle J_{\Delta }=\int _{-L/2}^{+L/2}x^{2}\rho \,\mathrm {d} x={\frac {1}{12}}\rho L^{3}={\frac {1}{12}}ML^{2}}$, (avec ${\displaystyle M=\rho L}$)

Ici, ${\displaystyle \rho }$ exprime une masse linéique (masse par unité de longueur).

Cela est vrai si l'axe de rotation passe par le milieu de la barre. La formule est différente si l'axe de rotation passe par son extrémité.

Dans le cas d'un carré de côté ${\displaystyle a}$, le moment d'inertie selon un axe perpendiculaire au plan du carré est, en son centre :

${\displaystyle J_{\Delta }=\int _{-a/2}^{+a/2}\int _{-a/2}^{+a/2}(x^{2}+y^{2})\rho \,\mathrm {d} x\mathrm {d} y={\frac {\rho }{6}}a^{4}={\frac {1}{6}}Ma^{2}}$, (avec ${\displaystyle M=\rho a^{2}}$)

Ici, ${\displaystyle \rho }$ exprime une masse surfacique (masse par unité de surface).

Dans le cas d'un rectangle de grand côté ${\displaystyle b}$ et de petit côté ${\displaystyle c}$, le moment d'inertie selon un axe perpendiculaire au plan du rectangle (ici l'axe Oz) est, en son centre[20] :

${\displaystyle J_{\Delta }=\int _{-b/2}^{+b/2}\int _{-c/2}^{+c/2}(x^{2}+y^{2})\rho (x,y)\,{\mathrm {d} }x{\mathrm {d} }y={\frac {\rho }{12}}bc^{3}+{\frac {\rho }{12}}cb^{3}={\frac {1}{12}}M(b^{2}+c^{2})}$, (avec ${\displaystyle M=\rho bc}$)

Ici, ${\displaystyle \rho }$ exprime une masse surfacique (masse par unité de surface) pour une surface homogène, elle ne dépend donc pas de x et y. Remarquons que si ${\displaystyle b=c}$, on se ramène au cas du carré.

Dans le cas d'un parallélépipède de hauteur ${\displaystyle h}$, de grand côté ${\displaystyle b}$ et de petit côté ${\displaystyle c}$, le moment d'inertie selon l'axe le long de sa hauteur et en son centre est le même que celui pour un rectangle. En d'autres termes, la hauteur du parallélépipède ne joue aucun rôle[19] :

${\displaystyle J_{\Delta }={\frac {1}{12}}M(b^{2}+c^{2})}$

On utilisera les coordonnées cylindriques pour simplifier les calculs. Dans le cas d'un cylindre de rayon ${\displaystyle R}$ et de hauteur ${\displaystyle h}$, le moment d'inertie selon l'axe de révolution Oz du cylindre est[21] :

${\displaystyle {J_{\Delta }}_{z}=\int _{0}^{R}r^{2}\rho 2\pi rh\,\mathrm {d} r={\frac {1}{2}}\rho \pi R^{4}h={\frac {1}{2}}MR^{2}}$, (avec ${\displaystyle M=\rho \pi R^{2}h}$)

Ici, ${\displaystyle \rho }$ exprime une masse volumique (masse par unité de volume).

On peut également déterminer le moment d'inertie selon tout axe Ox perpendiculaire à l'axe de révolution Oz du cylindre. Il vaut[22] :

${\displaystyle {J_{\Delta }}_{x}={\frac {MR^{2}}{4}}+{\frac {Mh^{2}}{12}}}$

Dans le cas d'un cylindre creux de rayons intérieur ${\displaystyle R_{1}}$ et extérieur ${\displaystyle R_{2}}$, et de hauteur ${\displaystyle h}$, le moment d'inertie selon l'axe du cylindre est[23] :

${\displaystyle J_{\Delta }=\int _{R_{1}}^{R_{2}}r^{2}(\rho 2\pi rh\,\mathrm {d} r)=2\rho \pi h\left[{\frac {r^{4}}{4}}\right]_{R_{1}}^{R_{2}}={\frac {1}{2}}\rho \pi h(R_{2}^{4}-R_{1}^{4})={\frac {1}{2}}M(R_{2}^{2}+R_{1}^{2})}$, (où la masse du cylindre ${\displaystyle M=\rho \pi h(R_{2}^{2}-R_{1}^{2})}$)

Ici, ${\displaystyle \rho }$ exprime une masse volumique (masse par unité de volume).

Pour un cône (plein) dont la base a un rayon ${\displaystyle R}$, son moment d'inertie le long de sa hauteur est[19] :

${\displaystyle J_{\Delta }={\frac {3}{10}}MR^{2}}$, avec ${\displaystyle M=\rho \,{\frac {\pi R^{2}h}{3}}}$.

A noter que l'expression du moment d'inertie en fonction de sa masse et du rayon de sa base ne dépend pas de la hauteur du cône.

Pour un tore de paramètres ${\displaystyle R}$ et ${\displaystyle r}$, son moment d'inertie selon son axe de révolution est[24]:

${\displaystyle J_{\Delta }=M\left(R^{2}+{\frac {3}{4}}r^{2}\right)}$

Pour un anneau fin (d'épaisseur négligeable) de rayon ${\displaystyle R}$ et de densité linéique (masse par unité de longueur) ${\displaystyle \mu }$, tous les éléments sont à la même distance de l'axe donc :

${\displaystyle J_{\Delta }=M\,R^{2}=(\mu \,2\pi R)R^{2}=2\pi R^{3}\mu }$

• Perez, Cours de physique : mécanique - 6^e édition, Masson, Paris, 2001, chapitre 17;
• Herbert Goldstein, Charles P. Poole Jr. et John L. Safko, Classical Mechanics [détail des éditions], chapitre 5;
• K. Gieck et R. Gieck (trad. G. Bendit), Formulaire technique, Gieck Verlag, 1997;
• Lev Landau et Evgueni Lifchits, Physique théorique, t. 1 : Mécanique [détail des éditions], chapitre 6.

• Moment cinétique
• Moment d'inertie normalisé
• Moment quadratique

• Portail de la physique