Mouvement de rotation

La rotation ou mouvement de rotation est l'un des deux mouvements simples fondamentaux des solides, avec le mouvement rectiligne. En génie mécanique, il correspond au mouvement d'une pièce en liaison pivot par rapport à une autre.

Sphère en rotation autour d'un de ses diamètres

La notion de mouvement circulaire est une notion de cinématique du point : on décrit la position d'un point dans le plan. La rotation est une notion de cinématique du solide : on décrit l'orientation d'un solide dans l'espace.

L'étude du mouvement de rotation est la base de la méthode du centre instantané de rotation (CIR).

Définition

Un solide est en rotation si la trajectoire de tous ses points sont des cercles dont le centre est une même droite ; cette droite est appelée « axe de rotation », et habituellement notée Δ[1].

En cinématique dans le plan, les trajectoires des points sont des cercles concentriques, le centre commun de ces cercles est appelé « centre de rotation » et habituellement noté O.

La rotation est donc un mouvement bien distinct de la translation circulaire, mouvement dans lequel les trajectoires des points sont également des cercles, mais de même rayon et de centres différents.

Orientation, vitesse angulaire, accélération angulaire

Cinématique plane

On se place dans le cadre d'un mouvement plan.

Définitions

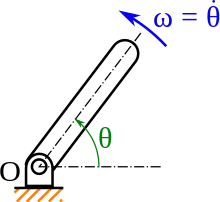
Définition de l'orientation et de la vitesse angulaire

L'orientation du solide est repérée par un angle habituellement noté θ (voir Angles d'Euler). En cinématique plane, cet angle peut être défini comme l'angle entre

une direction de référence passant par O, en général l'axe (Ox), et
une droite passant par O et par un point A donné du solide distinct de O.

La vitesse de rotation ω est définie par

\omega ={\dot {\theta }}={\frac {\mathrm {d} \theta }{\mathrm {d} t}}

.

l'accélération angulaire α est définie par

\alpha ={\dot {\omega }}={\frac {\mathrm {d} \omega }{\mathrm {d} t}}

soit également

\alpha ={\ddot {\theta }}={\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}

.

À l'instar du mouvement de translation et du mouvement circulaire, on distingue le mouvement de rotation uniforme et le mouvement de rotation uniformément varié.

Mouvement de rotation uniforme

Dans le cas du mouvement de rotation uniforme, on a une accélération angulaire nulle

α = 0

donc la vitesse de rotation est constante

ω = ω₀

et l'angle croît de manière linéaire

θ = θ₀ + ω₀×t

où θ₀ est l'orientation à l'instant initial. Ce mouvement idéal est en général utilisé pour décrire la partie centrale d'un mouvement (vitesse angulaire stable).

Mouvement de rotation uniformément varié

Dans le cas du mouvement de rotation uniformément varié, on a une accélération angulaire constante

α = α₀

donc la vitesse de rotation varie de manière uniforme

ω = ω₀ + α₀×t

où ω₀ est la vitesse à l'instant initial, et l'angle croît de manière quadratique

θ = θ₀ + ω₀×t + 1/2×α₀×t²

où θ₀ est l'orientation à l'instant initial. Ce mouvement idéal est en général utilisé pour décrire le début et la fin d'un mouvement (mise en route ou arrêt).

Mouvement des points

Triangle des vitesses dans le cas d'une barre en rotation

Triangle des vitesses dans le cas de points situés sur des axes différents

Chaque point M de l'objet a une trajectoire circulaire, donc décrit un cercle de centre O et de rayon R = OM. Le vecteur vitesse instantané est tangent au cercle, donc perpendiculaire au rayon [OM]. Sa norme vaut

v = ω×R.

Les équations horaires du point dans le cas des mouvements uniforme est décrit dans l'article Mouvement circulaire uniforme. Dans le cas général, elles sont décrites dans l'article Mouvement circulaire non uniforme.

Graphiquement, si l'on considère les vecteurs vitesse des points appartenant à une même droite passant par O, leurs extrémités sont sur une droite passant par O (en raison de la proportionnalité en R) ; la figure ainsi formée est appelée « triangle des vitesses ».

Cela permet une résolution graphique de problèmes cinématiques : si l'on connaît la vitesse d'un point du solide — par exemple point en contact avec un actionneur (extrémité de tige d'un vérin, dent d'engrenage), on peut déterminer le vecteur vitesse de tous les points du solide :

leur direction est perpendiculaire au rayon en ce point ;
la norme de la vitesse de tous les points situés sur un même cercle de centre O est identique ;
si l'on « rabat » les points sur une même droite passant par O, les vecteurs forment le triangle des vitesse.

Par « rabattre le point B sur la droite », on entend trouver le point B' de la droite situé sur le même cercle de centre O.

Cinématique dans l'espace

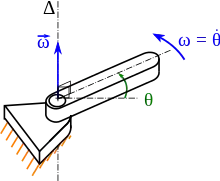
Position et vecteur vitesse de rotation

Dans le cas de la cinématique dans l'espace, on prend un axe de référence normal à l'axe de rotation et le coupant en O, et un point A du solide situé dans le plan normal à l'axe de rotation et passant par O.

Le vecteur vitesse de rotation ${\vec {\omega }}$ est le vecteur

ayant pour direction l'axe de rotation ;
dont le sens est déterminé par la règle conventionnelle d'orientation : règle de la main droite, sens de vissage ;
dont la norme est la dérivée de la position par rapport au temps.

Le vecteur accélération angulaire ${\vec {\alpha }}$ est la dérivée vectorielle de ${\vec {\omega }}$ :

{\vec {\alpha }}={\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}

Si O est un point de l'axe de rotation et A un point quelconque du solide, le vecteur vitesse ${\vec {v}}_{\mathrm {A} }$ en A est obtenu par

{\vec {v}}_{\mathrm {A} }={\overrightarrow {\omega }}\wedge {\vec {\mathrm {OA} }}

.

Le vecteur vitesse angulaire est la résultante ${\vec {\Omega }}$ du torseur cinématique. Le vecteur vitesse en A est le moment de ce torseur en ce point de réduction.

Torseur cinématique

Le torseur cinématique d'une rotation d'un solide 1 par rapport à un référentiel 0, exprimé dans un repère orthonormé ${\mathfrak {R}}(\mathrm {O} ,{\vec {x}},{\vec {y}},{\vec {z}})$ , est de la forme

\{{\mathcal {V}}_{1/0}\}={\begin{matrix}\\\\\\\end{matrix}}_{\mathrm {A} }{\begin{Bmatrix}\omega _{x}(t)&0\\\omega _{y}(t)&0\\\omega _{z}(t)&0\\\end{Bmatrix}}_{\mathfrak {R}}

où A est un point quelconque de l'axe de rotation. Le vecteur vitesse de rotation instantanée a pour composantes

{\vec {\Omega }}_{1/0}{\begin{pmatrix}\omega _{x}\\\omega _{y}\\\omega _{z}\end{pmatrix}}

Dynamique et énergétique

On peut appliquer la dynamique du point à chaque élément de matière du solide. En intégrant sur la totalité du solide, on trouve les résultats suivants :

l'inertie en rotation, ou inertie à la rotation, par rapport à l'axe Δ est exprimée par le moment d'inertie J_Δ ;
l'accélération angulaire est reliée aux couples extérieurs C_ext et aux moments des forces extérieures par rapport à l'axe $\mathrm {M} _{\Delta }({\vec {\mathrm {F} }}_{\mathrm {ext} })$ par le principe fondamental de la dynamique :

\mathrm {J} _{\Delta }\alpha =\sum \mathrm {C_{ext}} +\sum \mathrm {M} _{\Delta }({\vec {\mathrm {F} }}_{\mathrm {ext} })

ou, sous forme vectorielle

\mathrm {J} _{\Delta }{\vec {\alpha }}=\sum {\vec {\mathrm {C} }}_{\mathrm {ext} }+\sum {\vec {\mathrm {M} }}_{\Delta }({\vec {\mathrm {F} }}_{\mathrm {ext} })

.

Par ailleurs, l'énergie cinétique en rotation E_c s'exprime par

\mathrm {E_{c}} ={\frac {1}{2}}\mathrm {J} _{\Delta }\omega ^{2}

et le théorème de l'énergie cinétique énonce que la variation de l'énergie cinétique est égale à la somme des travaux des couples et moments internes et externes. Le travail d'un couple C constant entre deux positions θ₁ et θ₂ s'écrit

W_{θ₁→θ₂}(C) = C⋅(θ₂ - θ₁),

le paramètre (θ₂ - θ₁) étant l'amplitude du mouvement. Si le couple varie, on définit alors le travail élémentaire pour une petite rotation d'un angle dθ

dW_C = C⋅dθ

et

\mathrm {W} _{\theta _{1}\to \theta _{2}}=\int _{\theta _{1}}^{\theta _{2}}\mathrm {C} \cdot \mathrm {d} \theta

.

La puissance P du couple se définit par

P_C = C⋅ω.

Sous forme vectorielle, la puissance devient

\mathrm {P} _{\vec {\mathrm {C} }}={\vec {\mathrm {C} }}\cdot {\vec {\omega }}

.

Mise en œuvre de ce mouvement

Le mouvement de rotation est très utilisé pour les outils coupants ou abrasifs : fraisage, scie circulaire, meule. Le mouvement permet d'évacuer les copeaux.

Le mouvement de rotation permet un mouvement continu. Ainsi, lorsqu'une machine doit effectuer une série d'opérations, toujours les mêmes, sur un grand nombre de pièces, une des solutions consiste à mettre les articles sur une roue pour les faire passer devant les différents postes, ou bien à mettre les postes opératoires sur une roue pour les faire passer devant la pièce.

Le mouvement de rotation permet également de faire passer un objet d'un point à un autre, mais il ne conserve pas l'orientation de l'objet. C'est une solution de guidage économique — les paliers coûtent moins cher que les glissières — et robuste — les glissières peuvent se bloquer par arc-boutement. Si l'on a besoin de conserver l'orientation du sujet, on peut alors avoir recours à une translation circulaire, ou bien combiner la rotation « de transport » avec une rotation « d'orientation ».

Notes et références

Définitions lexicographiques et étymologiques de « rotation » (sens A1a) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales

Articles connexes

Portail du génie mécanique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] Définitions lexicographiques et étymologiques de « rotation » (sens A1a) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales