Trou noir de Kerr
En astrophysique, un trou noir de Kerr[1], ainsi désigné en l'honneur du mathématicien néozélandais Roy Kerr, est, par définition, un trou noir :
- de masse strictement positive : ;
- dont le moment cinétique n'est pas nul : , c'est-à-dire qui est en rotation axiale ;
- dont la charge électrique est nulle .
Pour les articles homonymes, voir Trou noir (homonymie).
Ne doit pas être confondu avec Trou noir de Kerr-Newman.
D'après la conjecture de calvitie, proposée par John Wheeler, il est un des quatre types théoriques de trous noirs[2].
Il est décrit, dans le cadre de la relativité générale, par la métrique de Kerr, une solution exacte, stationnaire et à symétrie axiale, de l'équation d'Einstein du champ de gravitation dans le vide[3], découverte par Roy Kerr en [4],[5] ; elle ne dépend que des deux paramètres et [3],[6], c'est-à-dire la masse et le moment cinétique [6],[7].
La métrique de Kerr ne décrit un trou noir qu'avec [6]. La métrique de Schwarzschild correspond au cas particulier de celle de Kerr[8]. Le trou noir extrémal que celle-ci décrit correspond au cas limite [6] ; la température de Hawking d'un tel trou noir est nulle[6]. Avec , la métrique de Kerr prédit l'existence de singularités nues[6], c'est-à-dire de singularités gravitationnelles qui, contrairement à celles des trous noirs sans rotation, ne seraient pas vraiment occultées par un horizon des évènements, hypothèse à laquelle s'oppose la conjecture de censure cosmique, proposée par Roger Penrose[9]. La métrique de Minkowski correspond au cas particulier de celle de Kerr[10].
Description
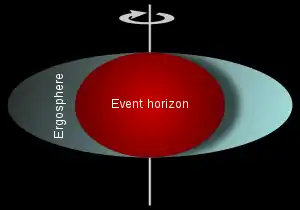
Contrairement au cas du trou noir sans rotation et sans charge électrique (appelé trou noir de Schwarzschild), la singularité gravitationnelle d'un trou noir de Kerr n'est pas ponctuelle mais annulaire.
D'autre part, un trou noir de Kerr possède deux horizons des événements[4],[11],[12] () : l'un extérieur (), l'autre intérieur () ; et deux surfaces limites de stationnarité : l'une externe, l'autre interne. La limite de stationnarité externe est l'ergosphère[13]. Alors que l'horizon des événements est décrit par une sphère de rayon , l'ergosphère est un ellipsoïde de révolution (oblate) dont le petit axe est aligné avec l'axe de rotation du trou noir et de même taille que , et le plan équatorial est de diamètre . De plus, . (voir la Fig. 1).
Singularité annulaire
Un trou noir de Kerr est associé à une singularité dite singularité de Kerr[14] dont la particularité est d'être, d'une part, annulaire[4],[14] — c'est-à-dire dont la topologie est celle d'un anneau — et, d'autre part, du genre temps[4],[14].
Horizon des évènements
La présence de l'horizon des évènements ne dépend pas de la rotation du trou noir, c'est une caractéristique commune à tous les types de trous noirs qui représente finalement l'essence même de ce qu'est un trou noir. Les particules qui franchissent l'horizon des évènements tombent définitivement dans le trou noir sans possibilité de s'en échapper.
Dans le cas d'un trou noir de Kerr, le rayon de l'horizon des évènements est appelé le rayon de Kerr[15] et s'écrit :
- ,
où :
- est la constante gravitationnelle ;
- est la vitesse de la lumière dans le vide ;
- est le rayon de Schwarzschild.
Il s'écrit aussi[15] :
- ,
où :
- est la constante gravitationnelle ;
- est la vitesse de la lumière dans le vide ;
- est la masse de l'objet ;
- est le paramètre de Kerr.
La valeur du rayon de l'horizon du trou noir de Kerr est donc comprise entre la moitié du rayon de Schwarzschild (quand le moment angulaire est maximal, ) et ledit rayon (moment angulaire nul, , cas du trou noir de Schwarzschild).
Ergosphère
L'ergosphère est dite limite statique en ce sens que les particules qui la franchissent sont obligatoirement entraînées dans le sens de rotation du trou noir, autrement dit, elles y possèdent un moment angulaire de même signe que . Cet entraînement confère du moment cinétique et de l'énergie mécanique à une particule qui pénètre dans l'ergosphère puis s'en échappe, de sorte que le trou noir voit son moment cinétique diminuer. C'est le processus de Penrose, qui permet de pomper de l'énergie à un trou noir en rotation.
L'ergosphère est décrite par l'équation polaire :
où, toutes notations égales par ailleurs, désigne l'angle par rapport à l'axe de rotation. Il s'agit d'un ellipsoïde de révolution de petit axe et de grand axe .
Métrique de Kerr
Taux de rotation du trou noir, et paramètre de spin
, le rapport entre le moment cinétique et la masse, définit le taux de rotation du trou noir et a pour dimension une masse. ne peut être supérieur à (voir espace-temps de Kerr rapide ci-dessous).
Le paramètre de spin est un paramètre sans dimension tel que , le signe représentant le sens de rotation.
Expression en coordonnées de Boyer-Lindquist
La métrique de Kerr s'écrit généralement dans les coordonnées de Boyer-Lindquist.
Elle est donnée par[16] :
- ,
avec :
- ,
- .
En posant et , elle est donnée par :
- ,
avec :
- ,
- ,
est la coordonnée temporelle, est la coordonnée radiale, est la colatitude, est la longitude.
Les points et sont les pôles et les points forment l'équateur. La droite joignant les pôles est l'axe de rotation du trou noir.
Le système de coordonnées est indéfini aux pôles. En effet, lorsque et , le coefficient g s'annule pour et .
De plus, les coordonnées sont invalides lorsque où le coefficient g diverge.
Les coefficients de la métrique (exprimée dans les coordonnées de Boyer-Lindquist) sont indépendants de et . Par conséquent, la géométrie de l'espace-temps est indépendante du temps (c'est-à-dire stationnaire) et à symétrie axiale.
Autrement dit, la métrique de Kerr possède les vecteurs de Killing :
Les composantes de la métrique de Kerr exprimées avec les coordonnées de Boyer-Lindquist sont remarquables car elles sont égales au produit scalaire des coordonnées indépendantes :
Notons que si le moment angulaire par unité de masse est nul, (donc ), on obtient la métrique de Schwarzschild. Si on ajoute la contrainte , on obtient l'espace de Minkowski.
Expression en coordonnées de Kerr
Il arrive que la métrique soit exprimée dans les coordonnées de Kerr où est la coordonnée de rotation du trou noir :
Dans ce cas, les coefficients sont indépendants de et .
Les relations qui relient les deux systèmes de coordonnées sont :
- ,
- .
Espaces-temps de Kerr
Il existe trois types différents d'espace-temps de Kerr suivant l'importance relative de et , autrement dit, suivant la vitesse du moment angulaire .
L'espace-temps de Kerr lent
L'espace-temps de Kerr est dit « lent » (slow Kerr space-time) pour [17]. La rotation est lente ().
possède alors deux racines réelles.
C'est la version de l'espace-temps de Kerr la plus souvent étudiée. L'espace-temps possède deux horizons, les sphères de rayon et disposées symétriquement à la sphère de rayon . Le lieu géométrique où est appelé indifféremment l'horizon externe ou l'horizon des événements. Concernant , on le nomme horizon interne ou horizon de Cauchy. Les deux horizons séparent l'espace-temps en trois parties distinctes nommées blocs de Boyer-Lindquist (Boyer-Lindquist Blocks) :
Bloc 1
C'est la région extérieure au trou noir. L'ergosphère[18] appartient à ce bloc. La limite statique est l'hypersurface définie par la racine supérieure de l'équation : , où le coefficient g s'annule. Si on définit l'ergosphère par la coordonnée radiale :
.
Cette équation permet de retrouver quelques résultats prévisibles :
La limite statique coïncide avec l'horizon des évènements aux pôles.
L'extension radiale de l'ergosphère est maximale à l'équateur du trou noir (Voir Fig. 1).
La limite statique se rapproche de plus en plus de l'horizon des évènements à mesure que le moment angulaire par unité de masse diminue.
Si un observateur franchit l'ergosphère, il lui est physiquement impossible de rester au repos par rapport à un objet extérieur au trou noir. De plus, tous les observateurs possédant une coordonnée radiale et une colatitude fixes se situant dans cette région de l'espace-temps de Kerr doivent décrire des orbites dans le même sens de rotation que le trou noir.
Si et , lorsque et .
Bloc 2
C'est la région située sous l'horizon externe. De la même manière que pour l'horizon de Schwarzschild caractérisant un trou noir sans rotation, aucun objet ne peut émerger de l'horizon des évènements.
Bloc 3
C'est la région de l'espace-temps située sous l'horizon interne contenant la singularité annulaire source de la gravité.
L'espace-temps de Kerr extrême
L'espace-temps de Kerr est dit « extrême » (extreme Kerr space-time) pour [17]. La rotation est critique ().
est la racine double de et la sphère de rayon est l'horizon unique.
Si on reprend les formules précédentes, on trouve que l'ergosphère est la région :
.
La métrique décrit un objet en rotation qui cesse d'être un trou noir, mais n'atteint pas la vitesse de rupture. La vitesse de rotation à la limite externe est égale à la vitesse de la lumière. Comme l'explique Jean-Pierre Luminet : "En langage newtonien, on dirait qu'à la surface d'un trou noir maximal les forces de répulsion centrifuges compensent exactement les forces d'attraction gravitationnelles."[19]
L'espace-temps de Kerr rapide
L'espace-temps de Kerr est dit « rapide » (fast Kerr space-time) pour [17]. La rotation est rapide ().
ne possède aucune racine réelle et l'espace-temps n'a pas d'horizon. Dans ce cas de figure, il n'y a pas de trou noir, et on parle alors de singularité nue. L'intérêt de cette solution particulière est plutôt limité puisque Werner Israel[20] a démontré dans les années 1980 que toute interaction d'un trou noir tournant à sa fréquence maximale ( ) tend à ralentir son moment angulaire. Il semblerait donc qu'il n'existe aucun moyen physique de "construire" un espace-temps de Kerr rapide. C'est l'idée formulée initialement par Roger Penrose appelée conjecture de la "Censure cosmique".
Mesure expérimentale du spin d'un trou noir

Depuis 2006, il est possible de mesurer expérimentalement le paramètre de spin de certains trous noirs[21]. Estimer le spin d'un trou noir est beaucoup plus difficile que d'estimer sa masse, car l'effet de la rotation du trou noir ne peut être mesuré que par ses effets sur de la matière observable à proximité du trou noir, comme un disque d'accrétion par exemple.
L'estimation du paramètre est réalisée en mesurant le rayon de la dernière orbite circulaire stable ( pour Innermost Stable Circular Orbit). La formule théorique donnant ce rayon, pour une masse du trou noir donnée, ne dépend que de et la relation entre les deux est directe[22]. est lui-même déterminé en mesurant le spectre des rayons X émis dans le disque d'accrétion par des binaires X, des étoiles orbitant autour d'un trou noir, ainsi que par la luminosité de ces émissions[21]. Ce spectre est comparé à celui donné par un modèle théorique d'accrétion (Idealized Thin Disk Model[23]), et les paramètres dont sont ajustés pour réaliser la meilleure corrélation entre le spectre et la luminosité mesurés, et le modèle[21]. Pour une masse de trou noir d'une dizaine de masses solaires, peut varier entre 15 km pour et 90 km pour , variabilité suffisamment grande pour influencer notablement le spectre[21].
Certains trous noirs semblent en rotation extrêmement rapide ( proche de 1), comme GRS 1915+105.
| Binaire X | Masse du trou noir () | |
|---|---|---|
| 4U 1543-47 | 9.4 ± 1 | 0.7 - 0.85 |
| GRO J1655-40 | 6.3 ± 0.27 | 0.65 - 0.8 |
| GRS 1915+105 | 14 ± 4.4 | 0.98 - 1 |
Notes et références
- Taillet, Febvre et Villain 2013, s.v.trou noir de Kerr, p. 699, col. 2.
- Taillet et al. 2009, encadré « trou noir de Kerr », p. 560, lire en ligne (consulté le 2 août 2014)
- Léauté 1968, résumé, p. 93.
- Taillet, Febvre et Villain 2013, s.v.trou noir de Kerr, p. 700, col. 1.
- Kerr 1963.
- Penrose 2007, § 31.15, p. 881.
- Léauté 1968, § 3, a), p. 97.
- Léauté 1968, § 2, (2), p. 96.
- Taillet et al. 2009, entrée « singularité nue », p. 504, lire en ligne (consulté le 2 août 2014)
- Léauté 1968, § 2, (1), p. 95-96.
- Gialis et Désert 2015, chap. 5, exercice 5.5, solution, 2, p. 172-173.
- Hobson, Efstathiou et Lasenby 2006, § 13.8, p. 323.
- Gialis et Désert 2015, chap. 5, exercice 5.5, solution, 4, p. 172-173.
- Taillet, Febvre et Villain 2013, s.v.singularité annulaire, p. 628, col. 1.
- Hawley et Holcomb 2005, p. 258.
- Chaskalovic 2009, p. 417.
- Nicolas 2002, § 6, p. 57.
- Le terme ergosphère du grec "ergon" signifiant "travail" a été introduit par R. Ruffini et J. A. Wheeler dans Ruffini R. et J. A. Wheeler, "Relativistic cosmology and space platforms", Proceedings of the Conference on Space Physics, European Space Research Organisation, Paris, France, p. 45-174.
- Luminet, Jean-Pierre, Les Trous noirs, Éditions du Seuil, Paris, 1992, p. 198.
- Israel, Werner, Third Law of Black Hole Dynamics, Physical Review Letters, 57-397.
- Mc Clintock, Narayan, Shafee Estimating the spins of stellar-mass black homes in Black Holes Space Telescope Science Institute, 2007
- Shapiro, Teukolsky Blacks Holes, White Dwarfs and Neutron Stars, Wiley, 1983
- Novikov, Thorne Blackholes DeWitt & DeWitt 1973
Voir aussi
Bibliographie
- [Chaskalovic 2009] (en) Joël Chaskalovic, « Gravitation theory for mathematical modelling in geomarketing », Journal of Interdisciplinary Mathematics, vol. 12, no 3, , art. no 5, p. 409-420 (DOI 10.1080/09720502.2009.10700633, résumé, lire en ligne).
- [Kerr 1963] (en) Roy P. Kerr, « Gravitational field of a spinning mass as an example of algebraically special metrics » [« Le champ gravitationnel d'une masse en rotation »], Phys. Rev. Lett., vol. 11, no 5, , art. no 23, p. 237-238 (DOI 10.1103/PhysRevLett.11.237, Bibcode 1963PhRvL..11..237K, lire en ligne).
- (en) Wheeler, Thorn, & Misner, 1973, Gravitation, Freeman and Company, San Francisco (ISBN 0716703440)
- (en) Exemple de travaux tentant de détecter la présence d'un trou noir de Kerr, ApJ, 69, L570 (2002)
- [Gialis et Désert 2015] Denis Gialis et François-Xavier Désert, Relativité générale et astrophysique : problèmes et exercices corrigés, Les Ulis, EDP Sciences, coll. « Grenoble Sciences », , 1re éd., 1, X-353 p., ill., 24 cm (ISBN 978-2-7598-1749-8, EAN 9782759817498, OCLC 920911577, notice BnF no FRBNF44394347, SUDOC 188192891, présentation en ligne, lire en ligne).
- [Hawley et Holcomb 2005] (en) John F. Hawley et Katherine A. Holcomb, Foundations of modern cosmology [« Les fondements de la cosmologie moderne »], New York, OUP, hors coll., , 2e éd. (1re éd. 1998), 1 vol., XIV-554 p., ill., 18,9 × 24,6 cm (ISBN 978-0-19-853096-1, EAN 9780198530961, OCLC 493355083, notice BnF no FRBNF41078993, Bibcode 2005fmc..book.....H, SUDOC 094303479, présentation en ligne, lire en ligne).
- [Hobson, Efstathiou et Lasenby 2006] (en) Michael P. Hobson, George P. Efstathiou et Anthony N. Lasenby, General relativity : an introduction for physicists [« Relativité générale : une introduction pour physiciens »], Cambridge et New York, CUP, hors coll., , 1re éd., 1 vol., XVIII-572 p., ill., 17,3 × 25,1 cm (ISBN 978-0-521-82951-9, EAN 9780521829519, OCLC 494550299, notice BnF no FRBNF40201855, SUDOC 123578671, présentation en ligne, lire en ligne).
- [Léauté 1968] Bernard Léauté, « Étude de la métrique de Kerr », Ann. IHP, Phys. théor., t. VIII, fasc. no 1, , art. no 6, p. 93-115 (résumé, lire en ligne).
- [Nicolas 2002] (en) Jean-Philippe Nicolas, « Dirac fields on asymptotically flat space-times », Dissertationes Math., vol. 408, , p. 1-85 (DOI 10.4064/dm408-0-1, résumé, lire en ligne).
- [Papapetrou 1966] Achilles Papapetrou, « Champs gravitationnels stationnaires à symétrie axiale », Ann. IHP, Phys. théor., t. IV, fasc. no 2, , art. no 1, p. 183-105 (résumé, lire en ligne).
- [Penrose 2007] Roger Penrose (trad. de l'angl. par Céline Laroche), À la découverte des lois de l'univers : la prodigieuse histoire des mathématiques et de la physique [« The road to reality : a complete guide to the laws of the universe »], Paris, O. Jacob, coll. « Sciences », , 1re éd., 1 vol., XXII-1061 p., ill., 15,5 × 24 cm (ISBN 978-2-7381-1840-0, EAN 9782738118400, OCLC 209307388, notice BnF no FRBNF41131526, SUDOC 118177311, présentation en ligne, lire en ligne).
- [Taillet, Febvre et Villain 2013] Richard Taillet, Pascal Febvre et Loïc Villain, Dictionnaire de physique, Bruxelles, De Boeck Sup., hors coll., , 3e éd. (1re éd. ), 1 vol., X-899 p., ill., 17 × 24 cm (ISBN 978-2-8041-7554-2, EAN 9782804175542, OCLC 842156166, notice BnF no FRBNF43541671, SUDOC 167932349, lire en ligne).
- [Wiltshire, Visser et Scott 2009] (en) David L. Wiltshire, Matt Visser et Susan M. Scott (éd.), The Kerr spacetime : rotating black holes in general relativity [« L'espace-temps de Kerr : trous noirs en rotation en relativité générale »], Cambridge et New York, CUP, hors coll., , 1re éd., 1 vol., XVI-362 p., ill., 18 × 25,3 cm (ISBN 978-0-521-88512-6, EAN 9780521885126, Bibcode 2009kesp.book.....W, SUDOC 132361817, présentation en ligne).
Articles connexes
Liens externes
- (en) Kerr Black Hole sur le site scienceworld.wolfram.com
- (en) Kerr Metric sur le site scienceworld.wolfram.com
- Portail de l’astronomie
- Portail de la physique