Loi Gamma

En théorie des probabilités et en statistiques, une distribution Gamma ou loi Gamma est un type de loi de probabilité de variables aléatoires réelles positives. La famille des distributions Gamma inclut, entre autres, la loi du χ² et les distributions exponentielles. Une distribution Gamma est caractérisée par deux paramètres qui affectent respectivement la forme et l'échelle de sa représentation graphique. Les distributions Gamma sont utilisées pour modéliser une grande variété de phénomènes, et tout particulièrement les phénomènes se déroulant au cours du temps où par essence, le temps écoulé est une grandeur réelle positive ; c'est le cas par exemple dans l'analyse de survie.

Loi Gamma
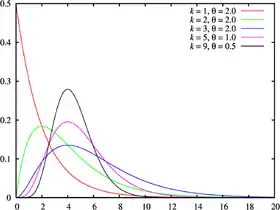Densité de probabilité


Fonction de répartition

Paramètres	$k>0\,$ réel $\theta >0\,$ réel
Support	$x\in [0,+\infty [$
Densité de probabilité	${\frac {x^{k-1}\mathrm {e} ^{-{\frac {x}{\theta }}}}{\Gamma (k)\theta ^{k}}}$
Fonction de répartition	${\frac {\gamma (k,x/\theta )}{\Gamma (k)}}$
Espérance	$k\theta \,$
Médiane	pas d'expression formelle
Mode	$(k-1)\theta \,$ pour $k\geq 1\,$
Variance	$k\theta ^{2}\,$
Asymétrie	${\frac {2}{\sqrt {k}}}$
Kurtosis normalisé	${\frac {6}{k}}$
Entropie	$k\theta +(1-k)\ln(\theta )+\ln(\Gamma (k))\,$ $+(1-k)\psi (k)\,$
Fonction génératrice des moments	$(1-\theta \,t)^{-k}$ pour $t<1/\theta$
Fonction caractéristique	$\left(1-i\theta t\right)^{-k}\,$

Définition et propriétés

Définition

Une variable aléatoire $X$ suit une loi Gamma de paramètres $k$ et $θ$ (strictement positifs), ce que l'on note aussi $X\,\sim \Gamma (k,\theta )$ (où $Γ$ est la majuscule de la lettre grecque gamma) si sa fonction de densité de probabilité peut se mettre sous la forme :

$f(x;k,\theta )={\frac {x^{k-1}\mathrm {e} ^{-{\frac {x}{\theta }}}}{\Gamma (k)\theta ^{k}}}$ ,

où $x > 0$ et $Γ$ désigne la fonction Gamma d'Euler.

Alternativement, la distribution Gamma peut être paramétrée à l'aide d'un paramètre de forme $α = k$ et d'un paramètre d'intensité $\beta =1/\theta$ :

$f(x;\alpha ,\beta )=x^{\alpha -1}{\frac {\beta ^{\alpha }\,\mathrm {e} ^{-\beta \,x}}{\Gamma (\alpha )}}\ \mathrm {pour} \ x>0$ .

Les deux paramétrages sont également répandus, selon le contexte.

Somme

Si chaque $X i$ suit la loi $Γ(k i, θ)$ pour i = 1, 2, ..., N, et si les variables aléatoires $X i$ sont indépendantes, alors :

$\sum _{i=1}^{N}X_{i}\sim \Gamma \left(\sum _{i=1}^{N}k_{i},\theta \right)$ .

Changement d'échelle

Pour tout $t > 0$ , la variable $tX$ est distribuée selon

Γ(k, tθ) où θ est le paramètre d'échelle

ou

Γ(α, β/t) où β est le paramètre d'intensité (rate parameter).

Lien avec les autres distributions

Contraintes sur les paramètres

Si $X\sim {\Gamma }(k=1,\theta =1/\lambda )\,$ , alors $X$ a une distribution exponentielle de paramètre $λ$ .
Si $X\sim {\Gamma }(k=\nu /2,\theta =2)\,$ , alors $X$ est identique à une variable $χ 2 (ν)$ , la distribution de la loi du χ² avec $ν$ degrés de liberté.
Si $k$ est un entier, la loi Gamma est une distribution d'Erlang.
Si $X^{2}\sim {\Gamma }(3/2,2a^{2})\,$ , alors $X$ a une distribution de Maxwell-Boltzmann avec comme paramètre $a$ .

Autres manipulations

Si X a une distribution Γ(k, θ), alors 1/X a une distribution loi Gamma inverse, de paramètres k et $θ -1$ .
Si X et Y sont distribuées indépendamment selon des lois Γ(α, θ) et Γ(β, θ) respectivement, alors X / (X + Y) a une distribution beta de paramètres α et β.
Si X_i sont distribuées selon des lois Γ(α_i, θ) respectivement, alors le vecteur (X₁ / S, ..., X_n / S), où S = X₁ + ... + X_n, suit une distribution de Dirichlet de paramètres α₁, ..., α_n.
Pour k grand, la distribution Gamma converge vers une loi normale, de moyenne $\mu =(k-1)\theta$ et de variance $\sigma ^{2}=(k-1)\theta ^{2}$ . De plus, quels que soient k et θ, en fixant de cette manière les constantes $\mu$ et $\sigma$ , les densités de probabilité de la distribution Gamma Γ(k, θ) et de la loi normale $N(\mu ,\sigma ^{2})$ ont alors deux points d'inflexion aux mêmes abscisses, à savoir $\mu +\sigma =\theta (k-1)+\theta {\sqrt {k-1}}$ et $\mu -\sigma =\theta (k-1)-\theta {\sqrt {k-1}}$ .

Propriété de concentration

Si $X\sim \chi ^{2}(k)$ , alors[1] pour tout $t>0$ , $\mathbb {P} \left(X\geq k+2{\sqrt {kt}}+2t\right)\leq e^{-t}$ et $\mathbb {P} \left(X\leq k-2{\sqrt {kt}}\right)\leq e^{-t}$ .

Références

(en) VERZELEN, Nicolas et GASSIAT, Elisabeth, « Adaptative estimation of high-dimensional signal to noise ratios », arXiv,‎ 16 mars 2017, p. 41 (lire en ligne)

Portail des probabilités et de la statistique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) VERZELEN, Nicolas et GASSIAT, Elisabeth, « Adaptative estimation of high-dimensional signal to noise ratios », arXiv,‎ 16 mars 2017, p. 41 (lire en ligne)