Médiane (statistiques)
En théorie des probabilités et en statistiques, la médiane est la valeur qui sépare la moitié inférieure de la moitié supérieure d'un ensemble (échantillon, population, distribution de probabilités). Intuitivement, la médiane est ainsi le point milieu de l'ensemble. C'est un indicateur de tendance centrale de la série. On peut déterminer une médiane pour un ensemble de valeurs non numériques[1] pour autant qu'on puisse choisir un critère d'ordonnancement de ces valeurs.
Pour les articles homonymes, voir Médiane.
Mode de calcul
Démarche générale
La méthode consiste à ordonner les valeurs en une liste croissante et à choisir la valeur qui est au centre de cette liste. Pour une liste ordonnée de n éléments, n étant impair, la valeur de l'élément à la position (n+1)/2 est la médiane. Si le nombre n d'éléments est pair, toute valeur comprise entre les éléments en positions (n-1)/2 et (n+1)/2 est une médiane[1] ; en pratique, dans le cas d'une liste de nombres, c'est la moyenne arithmétique de ces deux valeurs centrales qui est en général utilisée[2],[3].
La complexité de l'algorithme de calcul de la médiane est donc la complexité de l'algorithme de tri utilisé, soit au mieux O(n log n).
Exemples
- Ensemble de 7 entiers : {12; 5; 6; 89; 5; 2390; 1}. Après tri, la série est 1, 5, 5, 6, 12, 89, 2390. La médiane est le 4e élément de cette série, donc 6 : quatre valeurs de l'ensemble sont inférieures ou égales à 6, et quatre sont supérieures ou égales à 6.
- Ensemble de 6 entiers : {12; 5; 6; 89; 5; 1}. Après tri, la série est 1, 5, 5, 6, 12, 89. Toute valeur comprise entre le 3e et le 4e éléments de cette série, donc entre 5 et 6, peut être choisie comme médiane. Trois éléments sont inférieurs ou égaux à 5,6 et trois y sont supérieurs, donc 5,6 est une médiane, mais c'est aussi le cas de 5,141, de 5,9 ou de 5,5. On prendra généralement cette dernière valeur comme médiane puisqu'elle est la moyenne arithmétique des deux éléments centraux 5 et 6.
- Supposons 21 personnes dans une pièce. Chacune prend l'argent de sa poche et le pose sur une table : 20 personnes posent 5 euros, et la dernière pose 10 000 euros. La médiane est l'élément central, le onzième, de la liste ordonnée 5, 5, 5, …, 5, 10 000. C'est donc 5 : onze personnes détenaient chacune au moins 5 euros, et onze détenaient au plus 5 euros. On remarque que si la personne la plus riche ne s'était pas présentée, la médiane aurait été la même (5€), mais la moyenne aurait radicalement changé (5 € au lieu de 480,95 €).
- Un sondage express réalisé auprès de 50 utilisateurs de Wikipédia révèle que 12 des sondés se disent très satisfaits, 7 très insatisfaits, 20 plutôt satisfaits et les autres se disent plutôt insatisfaits. Cet ensemble de réponses peut être rangé par satisfaction croissante, et on obtient une liste de cinquante éléments dans cet ordre : 7 très insatisfaits, 11 plutôt insatisfaits, 20 plutôt satisfaits, 12 très satisfaits. Les deux éléments centraux, le 25e et le 26e, ont la même valeur : « plutôt satisfait ». Cette valeur est donc la valeur médiane de l'ensemble des réponses.
Autre démarche
Pour déterminer une médiane d'un ensemble de valeurs, il suffit de calculer les pourcentages cumulés croissants et on prend la première valeur de la série dont le pourcentage cumulé atteint ou dépasse 50 %.
Cette méthode est plus pratique lorsque l'on a un grand nombre de valeurs[Information douteuse].
Efficacité des algorithmes
Il existe des algorithmes de complexité linéaire (en O(n)), donc plus performants[4]. Il s'agit d'algorithmes qui permettent de manière générale de déterminer le k-ième élément d'une liste de n éléments (voir Algorithme de sélection) ; k = n/2 pour la médiane. Ce sont des adaptations des algorithmes de tri, mais qui sont plus performants du fait que l'on ne s'intéresse pas à toutes les valeurs. On peut par exemple utiliser l'algorithme diviser pour régner en seulement O(n) opérations ; c'est le cas de l'algorithme quickselect, variation du Tri rapide (quicksort), qui est en général en O(n) mais peut être en O(n2) dans le pire des cas.
Dans la pratique, si l'on cherche la médiane d'une liste de n entiers, et si l'on a la chance de constater que la valeur maximale m est inférieure à n2 (cette constatation coûte O(n)), alors le tri par comptage, de mise en œuvre très facile et dont le coût est, en l'espèce, de O(m) opérations, permet d'obtenir la médiane en moins de O(n2) opérations. Ce cas s'applique en particulier au cas des notes sur 20 (sans décimales) d'une classe de plus de 5 élèves (5 au carré est supérieur à 20).
Mesure de la dispersion statistique
Lorsque la médiane est utilisée pour situer des valeurs en statistiques descriptives, il existe différentes possibilités pour exprimer la variabilité : l'étendue, l'écart interquartile et l'écart absolu. Puisque la médiane est la même valeur que le deuxième quartile, son calcul est détaillé dans l'article sur les quartiles.
Médianes dans les distributions de probabilités
Pour toutes distributions de probabilités réelles, la médiane m satisfait l'égalité :
c'est-à-dire en termes de fonction de répartition :
Ainsi pour une distribution de probabilités diffuse (fonction de répartition continue) :
Médianes de certaines distributions
Pour toutes les distributions symétriques, la médiane est égale à l'espérance.
- La médiane de la loi normale d'espérance μ et de variance σ2 est μ. Pour cette distribution, espérance = médiane = mode.
- La médiane de la loi uniforme continue dans l'intervalle [a, b] est (a + b) / 2, qui est aussi l'espérance.
- La médiane de la loi de Cauchy avec le critère de position x0 et le paramètre d'échelle y est x0, le critère de position.
- La médiane de la loi exponentielle avec le facteur d'échelle λ est la division du logarithme népérien de 2 par le facteur d'échelle, soit (ln 2)/λ.
- La médiane de la distribution de Weibull avec le facteur de forme k et le facteur d'échelle λ est λ(log 2)1/k.
Médianes en statistiques descriptives
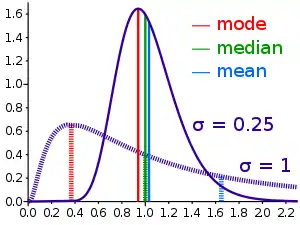
La médiane est principalement utilisée pour les distributions asymétriques, car elle les représente mieux que la moyenne arithmétique. Considérons l'ensemble { 1, 2, 2, 2, 3, 9 }. La médiane est 2, tout comme le mode, ce qui est une meilleure mesure de tendance centrale que la moyenne arithmétique égale à 3,166….
Le calcul de la médiane est couramment effectué pour représenter différentes distributions et elle est facile à comprendre, tout comme à calculer. Elle est aussi plus robuste que la moyenne en présence de valeurs extrêmes.
Propriétés théoriques
Propriété optimale
La médiane est aussi la valeur centrale qui minimise la valeur moyenne des écarts absolus. Dans la série {1, 2, 2, 2, 3, 9} donnée auparavant, ce serait (1 + 0 + 0 + 0 + 1 + 7) / 6 = 1,5, plutôt que 1,944 à partir de la moyenne, qui, elle, minimise les écarts quadratiques. En théorie des probabilités, la valeur c qui minimise
est la médiane de la distribution de probabilités de la variable aléatoire X.
Inégalité impliquant les moyennes et les médianes
Pour les distributions continues de probabilités, la différence entre la médiane et l'espérance est au plus d'un écart type.
Notes et références
- « Calcul de la médiane », Statistique Canada.
- Fabrice Mazerolle, « Médiane », (consulté le ).
- Eduscol, Baccalauréats professionnels Ressources pour la classe - Statistique et probabilités, 2009, p.2 (3)
- [(en) Selection (deterministic & randomized): finding the median in linear time]
Voir aussi
Articles connexes
Liens externes
- Portail des probabilités et de la statistique