Intervalle de confiance
En mathématiques, un intervalle de confiance encadre une valeur réelle que l’on cherche à estimer à l’aide de mesures prises par un procédé aléatoire. En particulier, cette notion permet de définir une marge d'erreur entre les résultats d'un sondage et un relevé exhaustif de la population totale.
Ne pas confondre avec l'intervalle de fluctuation ni avec le calcul d'incertitude en physique.
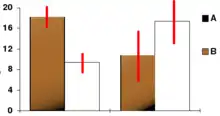
Un intervalle de confiance doit être associé à un niveau, en général sous la forme d’un pourcentage, qui minore la probabilité de contenir la valeur à estimer. Par exemple, un sondage auprès de 1000 personnes sur une question fermée (à laquelle on ne peut répondre que par « oui » ou par « non »), est valable à plus ou moins environ 3 points de pourcentage, au niveau de 95 % (c’est-à-dire que cette marge de 3 points est erronée moins d’une fois sur 20). Pour obtenir un intervalle plus réduit, donc plus précis, sans changer le nombre de sondés, il faut accepter un niveau plus faible, donc un plus grand risque de se tromper. Au contraire, pour réduire le risque d’erreur, on peut élargir l’intervalle.
Les intervalles de confiance sont souvent élaborés à partir d’un échantillon, c’est-à-dire une série de mesures indépendantes sur une population, notamment pour estimer des indicateurs statistiques comme la moyenne, la médiane ou la variance.
Mathématiquement, un intervalle de confiance est modélisé par un couple de variables aléatoires qui encadrent un paramètre réel, et ne doit pas être confondu avec l'intervalle de fluctuation, qui est déterminé par le paramètre et encadre une variable aléatoire. Mais c’est précisément en renversant les inégalités d’un intervalle de fluctuation, issu du théorème central limite ou de l’inégalité de Bienaymé-Tchebychev, que l’on peut obtenir l’expression d’un intervalle de confiance, comme celui qui estime l’espérance d’une loi à partir de la moyenne empirique et d’une majoration de l’écart type.
avec un écart type observé s sur un échantillon de taille n.
Exemple introductif : encadrement d'une proportion
Si on cherche à évaluer quelle proportion p de la population se reconnaitrait dans une catégorie donnée (qu’elle soit médicale, sociale, politique...), on peut poser la question à un nombre n d’individus (pas nécessairement différents) tirés au hasard et calculer la fréquence observée f définie comme le quotient du nombre de réponses positives par le nombre de sondés.
La loi des grands nombres assure qu’il est très probable que la fréquence observée soit proche de la proportion p. Mais le théorème central limite précise que la loi de probabilité qui décrit les valeurs possibles de f est proche d’une loi normale de paramètres p et . Avec cette approximation, on obtient un encadrement de la forme , où k est un coefficient indépendant de p et de n, qui provient des tables de la loi normale centrée réduite et qui est d’autant plus grand que l’on souhaite un niveau de confiance élevé, ce qui dégrade la précision. En particulier[1], pour un niveau de 90 %, on a k ≈ 1,645, mais pour un niveau de 95 %, on a k ≈ 1,96.
La résolution des inéquations apparaissant dans l’encadrement de f donne un encadrement[2] de p entre les bornes d’où par un développement asymptotique, on retrouve l’encadrement suivant qui définit l’intervalle de confiance classique : .
La symétrie des relations entre p et f dans ce contexte ne se vérifie pas forcément dans d’autres problèmes d’estimation. En outre, l’expression obtenue repose sur deux approximations successives, de la loi binomiale par la loi normale d’abord, puis de la fraction par les premiers termes du développement asymptotique ensuite.
Les inégalités et k < 2 mènent à l’approximation par un intervalle de confiance légèrement plus grand mais à la formulation plus simple[3] .
Principe général
On considère une famille de variables aléatoires (X1, ... , Xn), dont la loi conjointe est définie par un ou plusieurs paramètres inconnus. Il s’agit souvent d’un échantillon, c’est-à-dire que les variables sont indépendantes et identiquement distribuées, mais on peut traiter également des familles de variables provenant d’un processus stochastique.
Pour obtenir un intervalle de confiance sur l’un des paramètres λ, on peut essayer de calculer une nouvelle variable aléatoire Y = f(X1, ... , Xn, λ) à partir des précédentes et du paramètre à déterminer, dont la loi soit connue et dont on puisse exprimer des quantiles k1 et k2 tels que la probabilité soit égale (ou supérieure) au niveau de confiance souhaité. La résolution algébrique des inéquations k1 < f(X1, ... , Xn, λ) < k2 peut fournir alors un encadrement de λ qui constitue un intervalle de confiance.
Intervalles de référence
Loi normale
L’espérance et la variance d’une loi normale peuvent être estimées[4] à partir d’un échantillon (X1, ... , Xn).
Si l’écart type σ est connu, la moyenne empirique X suit une loi normale de même espérance μ et de variance σ2n, donc le quotient suit la loi normale centrée réduite. En utilisant un quantile k de cette loi, on obtient l'encadrement donc .
Si l’écart type n’est pas connu, il peut être estimé par , puis on calcule qui suit une loi de Student à (n – 1) degrés de liberté. Un encadrement par des quantiles –k < T < k donne l’intervalle de confiance défini par .
Pour estimer la variance, si l’espérance μ est connue, on peut calculer l’estimateur . Sachant que nTσ2 suit une loi du χ² (« khi-deux ») avec n degrés de liberté, l’encadrement par des quantiles k1 < nTσ2 < k2 donne un intervalle de confiance défini par .
Si l’espérance n’est pas connue, on calcule l’estimateur , sachant que nS2σ2 suit une loi du χ² avec (n – 1) degrés de liberté. L’encadrement par des quantiles k1 < nS2σ2 < k2 donne un intervalle de confiance défini par .
Loi uniforme
Pour un échantillon (X1, ... , Xn) de variables uniformes sur un intervalle [0, b], la variable M = max(X1, ... , Xn) a pour fonction de répartition F(x) = xnbn sur le même intervalle, d’où pour c = b n√α.
On obtient alors un intervalle de confiance défini par M < b < M α–1/n au niveau (1 – α).
Loi exponentielle
Si X est la moyenne empirique calculée à partir d’un échantillon (X1, ... , Xn) de variables exponentielles de paramètre λ > 0, le théorème central limite permet d’approcher la loi de par la loi normale centrée réduite, donc en considérant un quantile k de cette loi, on obtient un intervalle de confiance défini par .
Marge d'erreur sur un échantillon
À la fin du XVIIIe siècle, le mathématicien Laplace calcule le taux de natalité[5] sur quelques paroisses et en déduit la population de la France entière à partir du nombre total de naissances, consigné dans les registres de baptêmes de l'année[6]. Mais il va plus loin en joignant à cette évaluation par proportionnalité une estimation de l'erreur commise.
En effet, s'il est théoriquement possible que la valeur observée sur quelques cas particuliers corresponde exactement à la valeur sur l'ensemble de la population, il est théoriquement possible aussi que l'échantillon choisi ne soit pas du tout représentatif. Or le calcul de probabilités, qui s'est développé depuis le XVIe siècle, permet de décrire la probabilité qu'il y ait un écart donné entre ces deux valeurs. En fixant un seuil à cette probabilité, il est alors possible de majorer l'écart.
La dénomination « intervalle de confiance » est due à Jerzy Neyman[7].
Signification
La notion d'intervalle de confiance apparaît lorsqu'on tente d'obtenir des informations synthétiques sur une population que l'on ne connaît pas entièrement. Dans le cas contraire, en statistique descriptive, le problème se résout par des méthodes purement algébriques. Ici il faut associer à la population une loi de probabilité dont la pertinence doit être justifiée. La justification scientifique raisonnable consiste soit en une démonstration, soit en la pratique d'un très grand nombre d'observations, la loi des grands nombres étant la seule justification pratique de la notion de probabilité. Ceci conduit à interpréter un élément de la population comme une variable aléatoire et un échantillon comme un ensemble de telles variables.
En particulier, la moyenne et la variance, dites empiriques, calculées à partir de l'échantillon selon les règles algébriques applicables en statistique descriptive, sont elles-mêmes des variables aléatoires dont il est possible de calculer la moyenne et la variance, sous réserve d'indépendance des éléments de l'échantillon. Dans certains cas il est même possible de déterminer leur loi de probabilité. C'est ce qu'on appelle l'échantillonnage.
La moyenne empirique et la variance empirique calculées à partir de réalisations d'un échantillon fournissent donc des estimations aléatoires de la moyenne et de la variance de la loi de probabilité associée à la population.
Si on connaît la loi de probabilité d'une estimation on peut donc en déduire, pour une probabilité de non-dépassement donnée, un intervalle de confiance autour de la valeur estimée, défini comme l'intervalle dans lequel la probabilité a priori de l'estimateur est supérieure à une valeur donnée si la valeur réelle se trouve dans cet intervalle.
Ces notions, présentées ici de manière élémentaire, se généralisent dans la théorie des estimateurs.
Applications
Estimation d'une moyenne
L'usage le plus simple des intervalles de confiance concerne les populations à distribution normale (en forme de cloche) dont on cherche à estimer la moyenne X. Si on connaît l'écart type σ(X) (ou si on en connaît une estimation assez fiable) de cette distribution, et si on mesure la moyenne x sur un échantillon de taille n pris au hasard, alors
- l'intervalle est un intervalle de confiance de X à environ 68 %
- l'intervalle est un intervalle de confiance de X à environ 95 % [8]
- l'intervalle est un intervalle de confiance de X à environ 99,7 %
Ces formules sont valables pour des échantillons supposés infinis (n > 100). Dans le cas d'échantillon plus petit, la consultation d'une table de distribution de la loi de Student est nécessaire.
Encore faut-il connaître ou avoir une estimation de l'écart type σ(X). En pratique, on prend comme estimation de σ(X) la valeur s, l'écart-type de la série de mesures issues de l'échantillon.
Ainsi l'on voit que pour augmenter la confiance, il faut élargir l'intervalle et pour obtenir un intervalle plus fin avec même degré de confiance, il faut augmenter la taille de l'échantillon.
Sondage d'opinion
On cherche à estimer le pourcentage de personnes ayant une voiture rouge. Pour cela on effectue un sondage. Comme on ne sonde pas toute la population on a de bonnes chances de ne pas tomber exactement sur la bonne valeur mais de faire une erreur. On veut alors donner un intervalle qui a 95 % de chances de contenir la vraie valeur.
Pour cela on effectue un sondage sur 1 000 personnes. Les résultats sont les suivants : 150 personnes ont une voiture rouge, 850 n'en ont pas.
On appelle p la « vraie » proportion de personnes dans la population totale qui ont une voiture rouge. On cherche à estimer p. On appelle N le nombre de personnes ayant été sondées, ici N = 1000. On appelle S le nombre de personnes ayant une voiture rouge parmi les N personnes sondées. L’idée est de présenter comme estimation de p la valeur SN.
On applique le théorème central limite aux variables aléatoires X1,...,Xn où Xi vaut 1 si la i-ème personne sondée a une voiture rouge et 0 sinon. Chaque variable Xi suit une loi de Bernoulli de moyenne p et de variance p(1–p). Ces variables aléatoires ne sont mathématiquement indépendantes que si l'on laisse la possibilité de sonder éventuellement plusieurs fois la même personne dans le sondage (ce qui s'identifie à un tirage avec remise). Compte tenu de cette remarque, on applique le théorème central limite. Alors :
- tend vers une loi normale de moyenne 0 et de variance 1 (car S = X1 + ... + XN et N est assez grand).
Pour une loi normale de moyenne 0 et de variance 1 on a : P(−1,96 < Z < 1,96) = 0,95. La valeur -1,96 est le quantile d'ordre 2,5 % de la loi normale. Ces valeurs peuvent se trouver dans des tables de quantiles ou être calculées à partir de la fonction d'erreur réciproque : q = √2 erf-1(P) par exemple, q = √2 erf-1(0,95) = 1,9599... (voir par exemple les quantiles de la loi de Student pour un exemple de table de quantile.)
Soit encore
En estimant √p(1–p) par on peut alors encadrer p :
En fait si on appelle l'estimateur de la variance constatée, la variable suit une loi de Student à N-1 degrés de libertés. Ici, (N-1)=999 donc les quantiles d'ordre 999 de la loi de Student sont les mêmes d'un point de vue numérique que ceux d'ordre infini qui correspondent à la loi normale. On peut donc remplacer la variance par l'estimateur de la variance constatée.
Ensuite l'on peut remplacer l'erreur en pourcentage sur la variance constatée en omettant la normalisation NN–1 qui pour N = 1 000 est de l'ordre de 5/10000 que l'on néglige pour ne pas alourdir la présentation.- .
L'intervalle de confiance à 95 % vaut alors [0,127 ; 0,172]. On est sûr à environ 95 % qu'entre 12,7 % et 17,2 % de personnes ont une voiture rouge avec ce sondage[9].
Pour avoir une plus grande précision, il faudrait sonder plus de personnes. On remarque en effet l'existence d'un N apparaissant au dénominateur des deux racines carrées. Si on sonde plus de personnes (N plus grand), ces deux termes auront tendance à devenir plus petits et l'intervalle sera plus petit.
- Remarque
À la suite des diverses approximations du raisonnement, le résultat d'une confiance à 95 % n'est pas toujours assuré. On arrive à un résultat inférieur à 95 % pour certaines valeurs de p et N, par exemple
- si N = 100 et p = 0,5, alors ;
- si N = 100 et p = 0,37, alors ;
- si N = 150 et p = 0,4245, alors ...
- Cas particulier où le sondage porte sur un échantillon de taille non négligeable par rapport à celle de la population totale
On effectue un sondage sur N personnes différentes, prises aléatoirement dans une population totale de M individus. On suppose que N n'est pas négligeable devant M (par exemple N / M = 1/3), si bien que le théorème central limite ne s'applique plus vraiment (pour cause de non-indépendance des variables aléatoires décrites au-dessus). On appelle p la « vraie » proportion de personnes dans la population totale, et on appelle N le nombre de personnes ayant été sondées (par exemple N=1000). On appelle S le nombre de personnes ayant une voiture rouge parmi les N personnes différentes. Alors S suit une loi proche de la loi normale d'espérance Np et, non pas de variance Np(1-p), mais de variance Np(1-p)(1-N/M). Cette dernière est plus petite et réduit ainsi d'autant la longueur de l'intervalle de confiance qui est alors
- Cas particulier avec de faibles (ou fortes) probabilités
Si le résultat du sondage est qu'aucune personne n'a de voiture rouge sur les 1 000 interrogés, cela ne signifie pas qu'il n'existe aucune voiture rouge. Selon « la règle de trois »[10], l'estimation de la borne supérieure de l'intervalle de confiance est de 3/n soit 3/1 000 dans l'exemple. D'où l'estimation de 0 % de personnes possédant une voiture rouge avec un intervalle de confiance de [0 % ; 0,3%].
Estimation de l'espérance de la loi exponentielle
On cherche à estimer l'espérance X où X suit la loi exponentielle. On se fixe un niveau de confiance P ∈ ]0;1[ et on calcule q = √2 erf-1(P) (quantile d'ordre de la loi normale). Si on mesure la moyenne x sur un échantillon de taille n pris au hasard, alors l'intervalle est un intervalle de confiance de X à un niveau de confiance proche de P, cela quels que soient le niveau P ∈ ]0;1[ et la taille de l'échantillon n > q².
Par exemple, si la moyenne d'un échantillon de taille n = 20 est x = 3, alors l'intervalle de confiance à P=95 % est . Cela étant, lorsque la taille de l'échantillon et le niveau de confiance sont fixés, on peut calculer facilement un intervalle de confiance J de longueur inférieure à celle de I(n,q) et de manière exacte : par exemple, si on fixe n = 20 et P = 95 %, alors on obtient l'intervalle de confiance (qui donne environ [1,84 ; 4,41] lorsque x = 3) . Le lecteur en trouvera la preuve dans le premier exemple de la page 295 du livre de Delmas "Introduction au calcul des probabilités et à la statistique" (en référence ci-dessous).
De façon plus globale
L'intervalle de confiance mesure le degré de précision que l'on a sur les estimations issues de l'échantillon. Il y a deux sources principales de variations sur les données qui peuvent être la cause d'un manque de précision dans l'estimation d'une grandeur.
- Un nombre insuffisant de données : par exemple, dans le cas d'un sondage, on ne sonde pas toute la population mais qu'une fraction de la population. De même, pour les mesures physiques, on n'effectue qu'un nombre fini de mesures alors qu'il faudrait souvent en théorie pouvoir en faire une infinité pour obtenir un résultat parfait.
- Il peut également y avoir du bruit dans la mesure des données ce qui est pratiquement toujours le cas pour la mesure des grandeurs physiques.
Parmi les méthodes d'estimation, nous pouvons citer l'estimation par intervalle de confiance. Il s'agit de trouver un intervalle contenant un paramètre (inconnu) à estimer avec une probabilité ou niveau de confiance de 1–α. Pour p un paramètre (inconnu) à estimer, on souhaite déterminer a et b tels que :
ce qui est impossible. Par contre, si on appelle p la valeur exacte du paramètre, et que la valeur mesurée suit une loi de probabilité dépendant de p : , l'intervalle de confiance I(x) (au « niveau de confiance » 1–α) relatif à une observation x constatée, est l'intervalle dans lequel, pour toute valeur p,
- .
Pour un p donné, c'est la probabilité d'observer une valeur x pour laquelle le paramètre à estimer soit dans l'intervalle de confiance associé à cette observation x.
Ceci ne signifie pas que « la probabilité que la valeur réelle soit dans I(x) est 1–α », ce qui n'aurait pas de sens puisque la valeur réelle n'est pas une variable aléatoire. Cela signifie que « si la valeur réelle n'est pas dans I(x), la probabilité a priori du résultat de l'observation que l'on a obtenu était inférieure à α ». Par exemple si le paramètre n'est pas dans l'intervalle, c'est que l'observation effectuée correspond à un phénomène rare dans lequel l'intervalle de confiance ne contient pas la vraie valeur.
Notes et références
- Les valeurs de k indiquées correspondent au quantile double, puisque les intervalles sont symétriques par rapport à 0.
- Gilles Saporta, Probabilités, analyse de données et statistique, §13.5.4 « Intervalle de confiance pour une proportion p », Éditions TECHNIP, Paris 2011
- Voir par exemple le document ressource pour les probabilités de la classe de terminale en France, page 32, réalisé par le Ministère de l’éducation nationale en février 2012.
- Gilles Saporta, Probabilités, analyse de données et statistique, §13.5 « L’estimation par intervalles », Éditions TECHNIP, Paris 2011
- Plus précisément, il calcule son inverse, appelé « multiplicateur des naissances ».
- Alain Desrosières, « Le nombre et la constitution », Histoire des nombres, Éditions Tallandier, Paris 2007.
- Georges Morlat, « Statistique », Dictionnaire des mathématiques – fondements, probabilités, applications, Encyclopædia Universalis et Albin Michel, Paris 1998.
- l'intervalle de confiance à 95 % est plus précisément
- L’interprétation correcte de cette probabilité est la suivante. Si l’on prend 100 échantillons de 1 000 personnes et pour chaque échantillon on calcule un intervalle de confiance alors dans 95 de ces intervalles on trouve p et dans 5 la proportion p est en dehors. On a donc une confiance de 95 %.
- Hanley JA L-HA. If nothing goes wrong, is everythingall right?: Interpreting zero numerators. JAMA. avr 1983 ; 249(13):1743-1745.
Voir aussi
Articles connexes
Liens externes
- « Expérience numérique interactive d'intervalles de confiance », sur experiences.math.cnrs.fr
- Introduction au calcul des probabilités et à la statistique, livre de 315 pages.
Bibliographie
- Schenker N & Gentleman JF (2001) On judging the significance of differences by examining the overlap between confidence intervals. Am. Stat. 55, 182–186.
- Portail des probabilités et de la statistique