Intégrale multiple
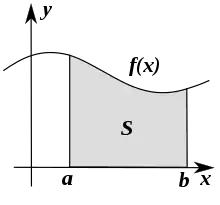
En analyse mathématique, l'intégrale multiple est une forme d'intégrale qui s'applique aux fonctions de plusieurs variables réelles. Les deux principaux outils de calcul sont le changement de variables et le théorème de Fubini. Ce dernier permet de ramener de proche en proche un calcul d'intégrale multiple à des calculs d'intégrales simples, et d'interpréter le « volume » d'un domaine « simple » de dimension n (ou son hypervolume si n > 3) comme l'intégrale d'une fonction de n – 1 variables (Fig. 2), de même que l'intégrale définie d'une fonction continue positive d'une variable est égale à « l'aire sous la courbe » associée (Fig. 1).
Définition
Soit f : D → ℝ une fonction bornée sur une partie bornée D de ℝn. Pour définir (au sens de Riemann) l'intégrabilité de f et, le cas échéant, la valeur de son intégrale, notée
ou plus simplement , on se ramène d'abord au cas où D est un pavé fermé P = I1 × … × In, en choisissant un tel P qui contient D et en prolongeant f par 0 (on démontre après coup que les définitions suivantes sont indépendantes du choix de P). Les définitions sont ensuite identiques, mutatis mutandis, à celles dans le cas n = 1 : à l'aide des notions de volume et subdivision de P et de pas, marquage et raffinement d'une telle subdivision, on définit l'intégrabilité et l'intégrale soit en termes d'intégrales inférieure et supérieure, soit en termes de sommes de Darboux inférieure et supérieure, soit en termes de sommes de Riemann, et l'on montre que ces trois définitions sont équivalentes[1]. La première, par exemple, s'écrit :
(c'est-à-dire que f est intégrable si et seulement si ses intégrales inférieure, , et supérieure, , sont égales, et l'intégrale de f est alors par définition cette valeur commune), et la troisième s'écrit :
où chaque (Pk, ξk)1 ≤ k ≤ N est une subdivision marquée de P de pas δ.
Dans les applications pratiques, comme l'ingénierie ou la physique appliquée, on rencontre quasi exclusivement des intégrales simples, doubles ou triples. L'intégrale, sur un domaine D de dimension n = 1, 2 ou 3, de la fonction constante 1, est respectivement la longueur, l'aire ou le volume de D.
Propriétés
Critère de Lebesgue
Le théorème de Lebesgue-Vitali étend aux fonctions de plusieurs variables le critère de Lebesgue pour l'intégrabilité de Riemann : une fonction bornée sur une partie bornée de ℝn est Riemann-intégrable si et seulement si l'ensemble des points de discontinuité de son prolongement par 0 à ℝn est négligeable[2]. En particulier :
Théorème — Toute fonction continue et bornée sur une partie cubable de ℝn est Riemann-intégrable[2].
En effet, une partie de ℝn est cubable (si et) seulement si elle est bornée et de frontière négligeable. Cette hypothèse de régularité du domaine est indispensable : une fonction continue sur un compact peut ne pas être intégrable (prendre, sur un compact non cubable, une fonction constante non nulle). Mais en pratique, tous les domaines considérés seront cubables, comme intersections finies de domaines « simples », au sens défini ci-dessous.
Propriétés élémentaires
Les autres propriétés des intégrales simples — linéarité, monotonie, etc. se généralisent également. On en déduit par exemple que si D est un compact connexe de ℝn, cubable mais non négligeable, et f : D → ℝ une fonction continue, alors il existe un point m de D en lequel la « valeur moyenne » ou « moyenne intégrale » de f sur D est atteinte, c'est-à-dire tel que
Cette propriété généralise le théorème de la moyenne en dimension 1, à cela près qu'en dimension supérieure, on n'est plus assuré de trouver un m intérieur à D.
Théorème de Fubini
Le théorème de Fubini pour les intégrales de Riemann est énoncé ci-dessous pour une intégrale double pour simplifier les notations, mais il se généralise en remplaçant ℝ×ℝ par ℝp×ℝq. De plus, on peut évidemment intervertir les rôles des deux variables (mono- ou multidimensionnelles) x et y.
Théorème[3] — Pour toute application f : [a, b]×[c, d] → ℝ :
Corollaire[4] — Lorsque f est Riemann-intégrable, les deux fonctions (intégrales inférieure et supérieure)
sont Riemann-intégrables et de même intégrale que f.
L'énoncé de la conclusion se simplifie[5] lorsque de plus, pour tout x ∈ [a, b], la fonction y ↦ f(x, y) est intégrable (sur [c, d]) : alors, son intégrale (fonction de x ∈ [a, b]) est intégrable et
Changement de variables
Soient U et V deux ouverts de ℝn, Φ : U → V un C1-difféomorphisme et f une application de V dans ℝ.
Ces hypothèses sont vérifiées dès que U et V sont cubables, f est continue bornée, et det JΦ est borné[7].
Méthodes d'intégration
Linéarité
Par linéarité, pour toute constante c, En particulier, l'intégrale d'une fonction constante égale à c, sur un domaine cubable D de ℝn, est le produit de c par le volume de D.
De même, l'intégrale d'une somme de fonctions intégrables peut être transformée en la somme de leurs intégrales :
En particulier, on peut partitionner le domaine d'intégration en un nombre fini de sous-domaines — ce qui revient à écrire f comme la somme des produits de f par les indicatrices de ces sous-domaines — puis appliquer la règle précédente. C'est ce qui remplace, en dimensions supérieures, la relation de Chasles propre à la dimension 1 :
Exploitation des symétries
Si la fonction est impaire par rapport à une variable xi et si le domaine est invariant par la symétrie par rapport à l'hyperplan xi = 0, l'intégrale s'annule.
Soit la fonction avec pour domaine d'intégration la boule unité de ℝ3. Le domaine présente une symétrie par rapport aux trois plans de coordonnées, mais comme la fonction est impaire par rapport à la variable x, il suffit de la symétrie par rapport au plan yOz pour annuler toute l'intégrale.
Réduction à des intégrales simples
La réduction en intégrales simples utilise le concept de domaine simple, de façon à exprimer l'intégrale en une composition d'intégrales simples. L'intégration est effectuée de l'intérieur vers l'extérieur, chaque fois par rapport à une seule variable en considérant les autres constantes, de la même façon que pour le calcul de dérivées partielles.
Domaines simples

Si A est une partie cubable de ℝn–1 et si deux fonctions g et h, définies sur A, sont Riemann-intégrables — par exemple si elles sont bornées et continues (éventuellement par morceaux) — alors la partie suivante de ℝn, appelée un « domaine simple orhogonal à l'hyperplan t = 0 », est cubable (Fig. 3) :
On peut bien sûr, dans cette définition et ce théorème, permuter les composantes des n-uplets de ℝn, pour choisir laquelle joue le rôle de t.
On peut également, dans la définition de D, remplacer un ou deux < par des ≤, car le graphe d'une fonction intégrable sur A est Jordan-négligeable.
Théorème
Si f est une fonction continue bornée sur ce domaine simple D, les hypothèses du critère de Lebesgue sont vérifiées, et le théorème de Fubini devient :
Réduction d'une intégrale double
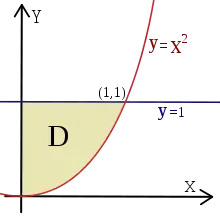
La région (Fig. 4) se présente comme le domaine simple (orthogonal à l'axe y = 0), associé aux deux fonctions g(x) = x2 et h(x) = 1, sur l'intervalle A = [0, 1] (on trouve l'extrémité 1, abscisse du point d'intersection des courbes de g et h, en calculant la solution positive de l'équation g(x) = h(x)).
On se propose d'intégrer sur D la fonction f(x, y) = x + y. Appliquons le théorème :
On calcule donc d'abord, pour x fixé :
puis l'intégrale définie :
Si l'on avait choisi de redéfinir D comme un domaine simple orthogonal à l'axe x = 0, on aurait obtenu les expressions :
conduisant au même résultat.
Réduction d'une intégrale triple
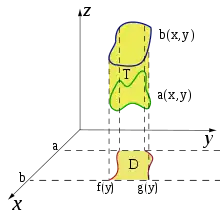
Considérons le domaine T de ℝ3 orthogonal au plan xy (Fig. 5)
Sa projection sur xy est le domaine D de ℝ2 orthogonal à x défini par[8]
Changements de variables usuels
Lorsque les méthodes précédentes ne sont pas efficaces (domaine difficile à exprimer ou fonction difficile à intégrer), un changement de variables permet parfois de reformuler l'intégrale de façon plus commode.
Coordonnées polaires

Dans ℝ2, si le domaine présente une symétrie circulaire (c.-à-d. décrit un secteur annulaire) et que la fonction a des caractéristiques particulières, on peut appliquer une transformation des coordonnées cartésiennes en coordonnées polaires, pour changer la forme du domaine et faciliter l'intégration.
D'après la définition de ce système de coordonnées, la transformation à effectuer est :
(avec r positif, et θ généralement choisi entre 0 et 2π).
Calcul du nouveau domaine
Le calcul du nouveau domaine U = Φ−1(V) s'effectue de façon automatique, en remplaçant x et y en fonction de r et θ dans les conditions sur (x, y) qui définissent l'ancien domaine V.
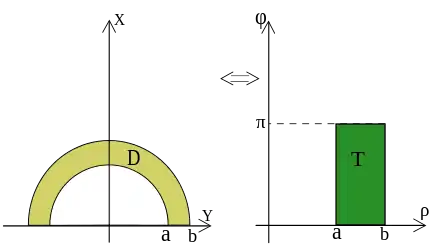
Si D = {(x, y) | a2 < x2 + y2 < b2, y > 0} avec b ≥ a ≥ 0 (Fig. 7), T := Φ−1(D) = {(r, θ) | a2 < r2 < b2, r sinθ > 0} = {(r, θ) | a < r < b, sinθ > 0} = ]a, b[×]0, π[.
Jacobien, intégration
La matrice jacobienne de l'application Φ au point (r, θ) est :
Son déterminant est donc égal à r, et l'on a, sous les hypothèses du théorème de changement de variables :
Soit f(x, y) = y à intégrer sur l'ouvert D de l'exemple précédent, qui correspond via Φ à l'ouvert T (r ∈ ]a, b[ et θ ∈ ]0, π[).
- donc
Coordonnées cylindriques
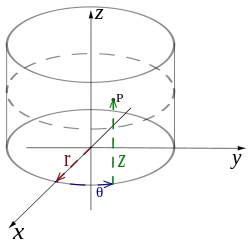
Dans ℝ3, l'intégration sur des domaines ayant pour base une portion de disque peut s'effectuer via un passage en coordonnées cylindriques :
Puisque la composante z est inchangée, le calcul du nouveau domaine et du jacobien sont calqués sur ceux du passage en coordonnées polaires, et l'on a :
Il est conseillé d'utiliser cette méthode dans les cas de domaines cylindriques, coniques, ou tout du moins de régions pour lesquelles il est commode tant de délimiter l'intervalle des z que de transformer la base circulaire et la fonction.
Soit f(x, y) = x2 + y2 + z à intégrer sur V = { (x,y,z) | x2 + y2 ≤ 9, 0 ≤ z ≤ 5 }. Alors,
et
En toute rigueur, U et V ne sont pas ouverts, le jacobien r s'annule en certains points de U, et Φ n'est même pas injective de U vers V. Mais il suffirait, pour remédier à tous ces problèmes, de remplacer le parallélépipède U par son intérieur et le cylindre V par Φ(U), et cela ne modifierait pas les intégrales (puisque les parties fermées qu'on supprime sont négligeables). Ce genre de raccourci, fréquent dans l'application du théorème de changement de variables proprement dit, sera désormais tacite. On obtient donc :
Coordonnées sphériques
.svg.png.webp)
Certains domaines de ℝ3 présentent une symétrie sphérique, ainsi il est possible d'exprimer les coordonnées de leurs points à l'aide de deux angles θ (longitude) et φ (colatitude) et d'une distance à l'origine ρ. Le passage en coordonnées sphériques est la transformation :
(avec ρ positif, θ compris entre 0 et 2π, et φ entre 0 et π) et son jacobien est :
Dès lors, on a (en se rappelant qu'il faut prendre la valeur absolue du jacobien) :
Il est conseillé d'utiliser cette méthode dans le cas de domaines sphériques et de fonctions facilement simplifiables à l'aide des identités trigonométriques, comme dans l'exemple du calcul du volume d'une boule ou l'exemple ci-dessous.
Intégrons f(x, y, z) = x2 + y2 sur V = {(x, y, z) | x2 + y2 + z2 ≤ R2} (boule de rayon R centrée à l'origine).
On termine le calcul en utilisant par exemple le changement de variable t = –cos φ :
et l'on conclut :
(Le passage en coordonnées cylindriques mènerait à des calculs un peu plus compliqués.)
Exemples d'applications : calculs de volumes
Grâce aux méthodes décrites précédemment, il est possible de démontrer les règles de calcul du volume de certains solides, en calculant l'intégrale triple sur ces solides la fonction constante 1.
Le volume d'un cylindre droit P = D×[0, h] (de base D et de hauteur h) se ramène à l'intégrale double ∬Dh dxdy sur le domaine D du plan xy. On retrouve ainsi, dans le cas particulier d'un cylindre droit, la formule classique : Volume d'un cylindre = aire base × hauteur.
Le volume d'une boule de rayon R est :
Grâce aux formules de réduction, on peut calculer le volume du 3-simplexe (le tétraèdre rectangle dont le sommet est à l'origine et les arêtes génératrices sont placées le long des trois axes et de longueur 1), en considérant, par exemple, l'orthogonalité selon le plan xy et l'axe x :
ce qui est conforme à la formule générale : Volume d'un cône = aire base × hauteur / 3, soit ici : (1/2) × 1 / 3.
Intégrale multiple impropre
Dans le cas de domaines non bornés ou d'intégrandes non bornés sur le bord du domaine, on parle d'intégrale multiple impropre.
Notes et références
- Jean-Pierre Ramis, André Warusfel et al., Mathématiques Tout-en-un pour la Licence 3, Dunod, (lire en ligne), p. 130-137.
- Ramis et Warusfel 2015, p. 155.
- (en) Xinwei Yu, « Fubini », sur Université de l'Alberta, (Honors Advanced Calculus I: Math 217).
- Démontré directement dans Ramis et Warusfel 2015, p. 160-161.
- Ramis et Warusfel 2015, p. 162.
- Ramis et Warusfel 2015, p. 165.
- Ramis et Warusfel 2015, p. 166.
- Une coquille s'est glissée dans la Fig. 5 : remplacer f(y) et g(y) par f(x) et g(x).
Voir aussi
Jacques Douchet et Bruno Zwahlen, Calcul différentiel et intégral : Fonctions réelles de plusieurs variables réelles, Lausanne, PPUR, , 2e éd. (1re éd. 1998), 172 p. (ISBN 2-88074-257-9)
- Portail de l'analyse
