Fonction bornée
En mathématiques, une fonction définie sur un ensemble à valeurs réelles ou complexes est appelée bornée si l'ensemble de ses valeurs est borné. Autrement dit, il existe un nombre réel tel que
pour tout x dans (on remarque que est nécessairement positif). Une fonction qui n'est pas bornée est dite non bornée.
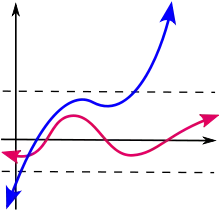
Si est à valeurs réelles et si pour tout dans , alors la fonction est dite majorée par . Si pour tout dans , alors la fonction est dite minorée par . Une fonction à valeurs réelles est bornée si et seulement si elle est à la fois majorée et minorée.
Un cas particulier important est celui d'une suite bornée, où est considéré comme l'ensemble des nombres naturels . Ainsi une suite est bornée s'il existe un nombre réel tel que
pour chaque entier naturel . L'ensemble de toutes les suites bornées forme l'espace des suites bornées, noté .
La définition de borne peut être généralisée aux fonctions à valeurs dans un espace plus général en exigeant que l'image soit un ensemble borné dans .
Notions connexes
La notion de borne locale est plus faible que la notion de borne. Une famille de fonctions bornées peut être uniformément bornée.
Un opérateur borné n'est pas une fonction bornée au sens de la définition de cette page (sauf si est la fonction nulle), mais a la propriété plus faible de préserver la notion de borne : les ensembles bornés sont envoyés sur les ensembles bornés . Cette définition peut être étendue à n'importe quelle fonction si et permettent le concept d'un ensemble borné.
Exemples
- La fonction est bornée.
- La fonction définie pour tous les réels x à l'exception de et est non bornée. À mesure que x s'approche ou , les valeurs de cette fonction deviennent de plus en plus grandes. Cette fonction peut être rendue bornée si l'on considère que son domaine est, par exemple, ou .
- La fonction définie pour tout réel x est bornée.
- La fonction trigonométrique inverse arc tangente définie comme est croissante pour tous les nombres réels x et est bornée pour radians.
- Chaque fonction continue est bornée. Plus généralement, toute fonction continue d'un espace compact dans un espace métrique est bornée (cf Théorème des valeurs extrêmes pour plus de détails).
- Toutes les fonctions à valeurs complexes qui sont entières sont soit non bornées soit constantes, conséquence du théorème de Liouville. En particulier, le sinus complexe doit être illimité car il est entier.
- La fonction qui prend la valeur si est un nombre rationnel et si est un nombre irrationnel (cf. Fonction Dirichlet ) est bornée. Ainsi, une fonction n'a pas besoin d'être "agréable" ou "gentille" pour être bornée. L'ensemble de toutes les fonctions bornées définies sur est beaucoup plus grand que l'ensemble des fonctions continues sur cet intervalle.
Remarques
- L’ensemble des fonctions réelles bornées sur un même ensemble constitue un sous-espace vectoriel stable aussi par multiplication, ce qui en fait une algèbre normée par la norme infini. Plus généralement, cet ensemble est stable par composition par une fonction continue. Cela implique notamment que toute variable aléatoire réelle bornée admet des moments à n’importe quel ordre.
- L’existence de bornes permet de justifier l’existence de limites finies pour une fonction croissante sur un intervalle.