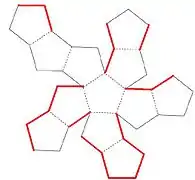
Dodécaèdre régulier
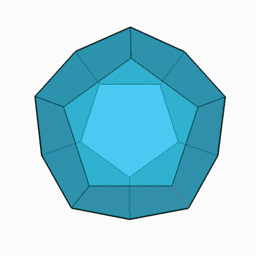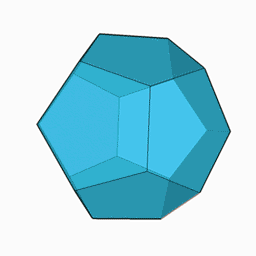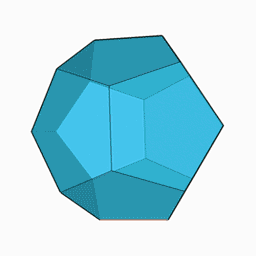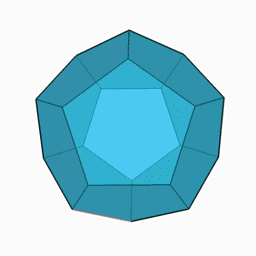
En géométrie, le dodécaèdre régulier (convexe) est un dodécaèdre dont les 12 faces sont des pentagones réguliers. Il possède 30 arêtes et 20 sommets. C'est un des 5 solides de Platon. Il possède une sphère circonscrite passant par ses 20 sommets et une sphère inscrite tangeante à ses 12 faces.
| Dodécaèdre régulier | |
| |
| Type | Solide platonicien |
|---|---|
| Faces | 12 pentagones réguliers |
| Arêtes | 30 |
| Sommets | 20 |
| Faces/sommet | 3 |
| Caractéristique | 2 |
| Symbole de Schläfli | {5,3} |
| Symbole de Wythoff | 3 |
| Diagramme de Coxeter-Dynkin | |
| Dual | Icosaèdre |
| Groupe de symétrie | Ih |
| Volume | |
| Aire | |
| Angle dièdre | arccos(-1/√5) (116,565 05°) |
| Propriétés | Convexe, régulier |
Comme il a 5 sommets par face, et 3 faces par sommet, son symbole de Schläfli est {5,3}.
Le préfixe dodéca-, douze en grec ancien , fait référence au nombre de faces. Son polyèdre dual est l'icosaèdre régulier (convexe).
Grandeurs caractéristiques
Si a est la longueur d'une arête :
- le rayon de sa sphère circonscrite est : où est le nombre d'or ;
- son aire est : ;
- son volume est : ;
- son angle dièdre (entre deux faces) vaut : ;
- les 20 points de coordonnées sont les sommets d'un dodécaèdre régulier centré sur l'origine et d'arête .
Symétries
Le dodécaèdre admet un centre de symétrie.
Les isométries laissant globalement invariant le dodécaèdre régulier forment un groupe. Ce groupe contient :
- les rotations d’axe passant par 2 sommets opposés et d'angle 2π/3 ou 4π/3 (120° et 240°). Il y a 10 couples de sommets opposés, donc 20 rotations de ce type ;
- les rotations d’axe passant par le centre de 2 faces opposées et d'angle 2π/5, 4π/5, 6π/5, ou 8π/5 (72°, 144°, 216° et 288°). Comme il y a 6 couples de faces opposées, il y a 24 rotations de ce type ;
- les rotations d'un angle π (180°) autour d'un axe par le milieu de 2 arêtes opposées (ces rotations sont aussi des symétries axiales). Il y a 15 couples d’arêtes opposées, et donc 15 rotations de ce type ;
- la symétrie s par rapport à son centre;
- les symétries par rapport à un plan passant par le centre et perpendiculaire à un des 15 axes cités plus haut ;
- etc.
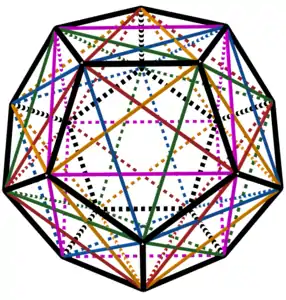
Avec l'identité, les 20 + 24 + 15 rotations énoncées forment un sous-groupe de 60 éléments isomorphe au groupe alterné A5. Une rotation quelconque permute en effet les cinq cubes qui composent le dodécaèdre, et inversement, une quelconque permutation paire des cinq cubes définit une unique rotation.
De même, l'identité et la symétrie s forment un autre sous-groupe noté C2.
Le groupe des isométries noté est le produit de ses deux sous-groupes ;
il contient 120 éléments.
Propriétés diverses
Le dodécaèdre régulier et l'icosaèdre régulier sont duaux l'un de l'autre, c'est-à-dire que le polyèdre ayant pour sommets les centres des faces de l'un est l'homothétique de l'autre.
Le squelette du dodécaèdre régulier — l'ensemble de ses sommets reliés par ses arêtes — forme un graphe appelé graphe dodécaédrique.
Platon mettait en correspondance le dodécaèdre avec le Tout parce que c'est le solide qui ressemble le plus à la sphère. Aristote a nommé ce cinquième élément, aithêr (aether en latin, « éther » en français) et a postulé que l'univers était fait de cet élément, et qu'il était substantiel à tous les autres, qu'il les contenait tous.
Soit O le centre du dodécaèdre (point équidistant de ses sommets) et A un sommet. La droite OA recoupe le dodécaèdre en un second point K, qui est soit le centre d’une face, soit le milieu d’une arête, soit un sommet. Or les deux rotations d’axe OA et d’angles respectifs 1/3 et 2/3 tour transforment le dodécaèdre en lui-même. K ne peut donc être qu'un sommet, et le symétrique du sommet A par rapport à O est le sommet K.
Le dodécaèdre admet cinq triplets de plans orthogonaux passant par le centre et qui sont chacun des plans de symétrie du dodécaèdre.
Soit AB une arête de milieu M et KL l’arête symétrique de AB par rapport au centre O.
La symétrie par rapport au plan perpendiculaire à OM passant par O est le produit de la rotation d’un demi-tour d’axe OM par la symétrie de centre O.
La symétrie S d’axe passant par O et parallèle à AB et qui transforme AB en LK, fait partie des 15 rotations du groupe H d’un demi-tour conservant le dodécaèdre. La symétrie par rapport au plan passant par O et perpendiculaire à AB est le produit de S par la symétrie de centre O.
La symétrie T d’axe passant par O et perpendiculaire au plan AOB et qui transforme AB en KL, fait partie des 15 rotations du groupe H d’un demi-tour conservant le dodécaèdre. La symétrie par rapport au plan passant par AOB est le produit de T parla symétrie de centre O
Les trois plans orthogonaux passant par O, respectivement perpendiculaires à OM, à AB et aux deux précédents, sont donc trois des quinze plans de symétrie du dodécaèdre. Par quatre rotations d’angles 1/5, 2/5, 3/5 et 4/5 de tour, d’axe commun avec la face contenant A et ne contenant pas B, on obtient quatre autres triplets de plans orthogonaux de symétrie.
Construction
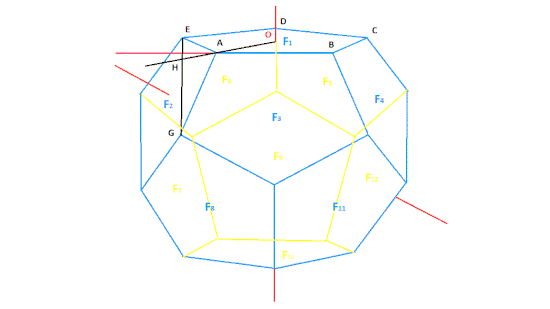
1. Construction des trois premières faces.
Soit ABCDE un pentagone régulier constituant la première face F1, de centre O et d’arête de longueur a. Dans le plan ABC, la perpendiculaire à AB passant par E coupe la droite OA en H. Dans le plan passant par OAH et perpendiculaire au plan ABC, soit G un des deux points d’intersection de la perpendiculaire au plan en H avec le cercle de centre A et de rayon a. Les points E et G sont dans un même plan perpendiculaire à AB, et à la même distance de AB. Il existe donc une rotation d’axe AB transformant E en G. Soit F3 la transformée de F1 par cette rotation : c’est un pentagone régulier ayant l’arête commune AB avec F1. Soit F2 le symétrique de F3 par rapport au plan OAG : c’est un pentagone régulier ayant l’arête commune AB avec F1 et ayant l’arête commune AG avec F3.
2. Construction des trois faces suivantes.
Soit R la rotation d’axe passant par O et perpendiculaire au plan ABC et de 1/5 de tour. Elle transforme la face F2 en la face F3, car les plans EAG et ABG forment le même angle avec le plan ABC. Soient F4, F5 et F6 les transformées de F2 par les rotations respectives R2, R3 et R4. F2 a une arête commune avec F3, donc F6 a une arête commune avec R4(F3), qui est égal à R5(F2), soit F2.
3. Construction des six dernières faces.
Soit S la rotation d’axe passant par le centre de la face F2 et perpendiculaire à celle -ci, et de 1/5 de tour. Elle transforme les faces F1 et F3 respectivement en les faces F6 et F1, car les plans de F1, de F3 et de F6 forment le même angle avec le plan de F2. Par ailleurs, la face F4 a une arête commune avec F1 et une arête commune avec F3, mais aucune arête commune avec F2. Sa transformée S(F4) a donc une arête commune avec F6 et avec F1, mais aucune avec F2 : c’est donc F5.
Soient F7 et F8 les transformées de F1 par les rotations respectives S2 et S3. F1 ayant une arête commune avec F6, F8 a une arête commune avec F3.
Soient F9, F10 et F11 les transformées de F4 par les rotations respectives S2, S3 et S4. F4 ayant une arête commune avec F5, F11 a une arête commune avec F4.
L’arête de F4 qui n’est commune avec aucune des dix autres faces précédemment définies, est transformée par S, S2, S3 et S4 en une arête respectivement de F5, F9, F10, et F11, qui sont dans un même plan et forment un pentagone régulier, douzième face du dodécaèdre.
Utilisations
Le poète médiéval Jean de Meung (1240-1305) a décrit un jeu de société divinatoire, dénommé « dodechedron », qui utilise un dé en forme de dodécaèdre régulier, dont chacune des douze faces représente un des signes du Zodiaque[1].
Le Megaminx est un casse-tête dérivé du Rubik's cube en forme de dodécaèdre régulier.
Certains jeux de rôles sur table utilisent dans leur système de jeu des dés à 12 faces pour la résolution d'actions. Ces dés à 12 faces sont des dodécaèdres.
Notes et références
- Jean de Meung, Le dodechedron de fortune : livre non moins plaisant et récréatif, que subtil et ingénieux entre tous les jeux et passe temps de fortune, Nicolas Bonfons, Paris, 1577.
Articles connexes
- Composé de cinq cubes (en)
- Dodécaèdre romain
- Espace dodécaédrique de Poincaré
- Portail de la géométrie