Coordonnées barycentriques
En géométrie affine, les coordonnées barycentriques d'un point par rapport à un repère barycentrique sont une famille de poids permettant de définir ce point comme un barycentre.
Définitions
Base affine
Une famille finie (P0,…,Pk) de points d'un espace affine E est dite affinement libre, ou encore ces points sont dits affinement indépendants, quand aucun des points Pi n'appartient au sous-espace affine engendré par les k autres points. Dans le cas contraire il est dit affinement lié. Par exemple deux points distincts forment une famille affinement libre, de même 3 points non alignés, et 4 points non coplanaires[1].
De façon équivalente une famille finie (P0,…,Pk) est affinement libre quand l'une des conditions suivantes est réalisée :
- aucun des points Pi n'est barycentre des autres points ;
- la famille de vecteurs est libre (ou la condition analogue en prenant n'importe lequel des Pi comme origine).
Il suit de la seconde condition et des propriétés des familles libres des espaces vectoriels qu'une famille affinement libre d'un espace affine de dimension finie n est d'ordre au plus n + 1. On appelle alors base affine (et très souvent repère affine) une famille affinement libre maximale, et la seconde condition devient :
(P0,…,Pn) est une base affine de l'espace affine E si et seulement si est une base vectorielle de la direction de E, c'est-à-dire si et seulement si P0 muni de cette famille de vecteurs est un repère affine (très souvent appelé un repère cartésien) de E.
Une base affine d'un espace affine E de dimension finie n est donc une famille affine libre (P0,…,Pk) de n + 1 points. Ainsi 2 points distincts d'une droite forment une base affine de celle-ci, 3 points non alignés d'un plan forment une base affine de ce plan, 4 points non coplanaires d'un espace de dimension 3 une base de celui-ci, etc.
L'espace affine engendré par (P0,…,Pn), c'est-à-dire le plus petit sous-espace affine contenant ces points, est l'espace affine E tout entier si ces points forment une base affine de E.
Coordonnées barycentriques
Soit (P0,…,Pn) une base affine, encore appelée repère barycentrique ou encore repère affine d'un espace affine E. Alors, tout point M de l'espace affine peut s'écrire comme un barycentre des points du repère, c'est-à-dire qu'il existe n + 1 scalaires vérifiant :
- avec
et de plus deux systèmes de scalaires vérifiant ceci sont multiples l'un de l'autre.
On appelle alors coordonnées barycentriques, ou coefficients barycentriques, du point M un tel système de « poids » , et les coordonnées barycentriques de M ne sont pas uniques, mais seulement uniques à un coefficient multiplicateur non nul près. Elles peuvent être définies de manière unique en fixant la somme des coordonnées à 1 : de telles coordonnées sont dites normalisées.
Dans le plan
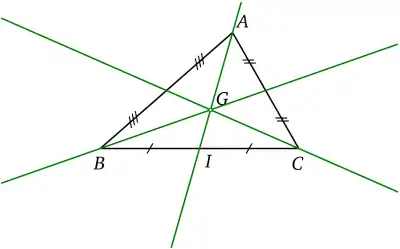
Dans le plan, les trois sommets d'un triangle ABC non aplati constituent un repère barycentrique. Son centre de gravité G est le point de coordonnées barycentriques (1,1,1) par rapport au repère (A,B,C).
En notant I le milieu de [BC], G a pour coordonnées barycentriques (1,2) par rapport au repère (A,I) de la droite (AI).
Dans ce triangle, le point I est de coordonnées (0,1,1) par rapport au repère (A,B,C).

La notion d'aire, bien que souvent introduite en géométrie euclidienne, est une notion affine. Plus précisément, c'est l'aire algébrique d'un triangle orienté dans le plan que l'on définit, rapportée à l'aire d'un triangle orienté choisi comme unité (ou du parallélogramme d'une base constitué de deux vecteurs, l'ordre des vecteurs n'étant pas indifférent)[2]. C'est en fait le rapport d'aires algébriques dans un même plan qui se définit par le déterminant.
Il est alors possible d'interpréter les coordonnées barycentriques dans le plan en terme d'aire[3].
Coordonnées barycentriques, déterminant et aire
Soit ABC un triangle non plat, c'est-à-dire que (A,B,C) est un repère barycentrique. Alors un point quelconque du plan du triangle P, a pour coordonnées les trois déterminants suivants (relatifs à une base quelconque du plan) :
c'est-à-dire que :
avec :
- .
Si la base choisie est , ce sont donc les coordonnées normalisées (α, β, γ) vérifiant
et ces coordonnées normalisées s'interprètent comme des rapports d'aires algébriques de la façon suivante :
En géométrie réelle, l'aire géométrique usuelle est la valeur absolue de l'aire algébrique. Le résultat vaut pour l'aire géométrique si le point est à l'intérieur du triangle. S'il est à l'extérieur, les signes des coefficients dépendent de l'orientation des triangles considérés (positif si l'orientation est la même que celle du triangle ABC, négative dans le cas contraire, voir schéma).
Exemples
Voici les coordonnées barycentriques de quelques points remarquables du triangle :
- milieu de
- milieu de
- milieu de
- centre de gravité
- centre du cercle inscrit ou
- centre du cercle circonscrit ou ou encore .
- orthocentre ou
- centre du cercle d'Euler
- point symédian
On trouvera dans l'encyclopédie des centres de triangle (ETC) les coordonnées barycentriques de milliers de points remarquables du triangle.
Convexité
L'enveloppe convexe d'un ensemble de points E rassemble tous les points admettant des coordonnées barycentriques à coefficients tous positifs par rapport à une famille de points de E[4].
Lien avec les coordonnées cartésiennes
Dans un espace vectoriel muni d'une base , la famille de vecteurs constitue un repère barycentrique pour la structure d'espace affine canonique et tout vecteur de coordonnées relativement à la base , correspond au point affine de coordonnées barycentriques , où s est la somme des coefficients .
Lien avec les coordonnées projectives
Les coordonnées projectives peuvent être interprétées comme des coordonnées barycentriques dans un repère formé de l'origine et des points à l'infini des axes.
Notes et références
- Par exemple Ladegaillerie 2003, p. 27-28, et pour l'ensemble du paragraphe.
- Ladegaillerie 2003, p. 24.
- Ladegaillerie 2003, p. 49.
- Marcel Berger, Géométrie [détail des éditions], Prop. 11.1.8.4, tome 3, p. 26 dans l'édition de 1978.
Bibliographie
- Yves Ladegaillerie, Géométrie : affine, projective, euclidienne et anallagmatique, Paris, Ellipses, , 515 p. (ISBN 2-7298-1416-7).
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-916352-08-4)
- Petite encyclopédie de mathématique, éd. Didier
- Jean Fresnel, Méthodes modernes en géométrie
Voir aussi
Articles connexes
Liens externes
- Les coordonnées barycentriques des points remarquables dans un triangle sur le site Math Web.
- Cours sur les coordonnées barycentriques par Jean-Louis Tu, dans le cadre de la préparation aux Olympiades de mathématiques.
- Méthodes de détermination d'appartenance d'un point à un triangle avec les coordonnées barycentriques.
- Portail de la géométrie