Enveloppe convexe
L'enveloppe convexe d'un objet ou d'un regroupement d'objets géométriques est l'ensemble convexe le plus petit parmi ceux qui le contiennent.
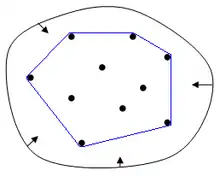
Dans un plan, l'enveloppe convexe peut être comparée à la région limitée par un élastique qui englobe tous les points qu'on relâche jusqu'à ce qu'il se contracte au maximum. L'idée serait la même dans l'espace avec un ballon qui se dégonflerait jusqu'à être en contact avec tous les points qui sont à la surface de l'enveloppe convexe.
Définition et propriétés élémentaires
On supposera être dans un contexte où la notion de sous-ensemble convexe a un sens (par exemple en géométrie affine sur les réels), et l'on notera E le cadre géométrique où l'on se place.
Définition — Soit A une partie de E. L'enveloppe convexe de A est l'intersection de toutes les parties convexes de E qui contiennent A.
Cette définition a un sens, puisqu'il existe au moins une partie convexe de E qui contient A, à savoir E lui-même.
De cette définition et du fait qu'une intersection quelconque d'ensembles convexes est un ensemble convexe, on déduit la caractérisation suivante de l'enveloppe convexe.
Proposition — L'enveloppe convexe de A est la plus petite partie convexe de E qui contient A.
Développé de façon plus détaillée, ce résultat caractérise l'enveloppe convexe Conv(A) comme l'unique sous-ensemble de E qui vérifie les trois conditions suivantes :
- Conv(A) est convexe ;
- A est inclus dans Conv(A) ;
- si C est un sous-ensemble convexe de E contenant A, alors Conv(A) est inclus dans C.
Par exemple, Conv(∅) = ∅.
Description en termes de barycentres
Dans la suite de cette section, on supposera que E est un espace affine réel. On peut alors énoncer[1] :
Proposition — L'enveloppe convexe de A est l'ensemble des combinaisons convexes (c'est-à-dire des barycentres à coefficients positifs ou nuls) de familles de points de A.
Autrement dit : les éléments de l'enveloppe convexe de A sont exactement les points x de E qu'on peut écrire sous la forme :
- , expression dans laquelle p est un entier, les ai sont dans A, les coefficients λi sont réels positifs et de somme
Le cas de la dimension finie : un théorème de Carathéodory
L'énoncé qui précède peut être amélioré en dimension finie, comme remarqué par Constantin Carathéodory en 1907. Si l'on note n la dimension de E, le théorème affirme qu'on peut utiliser des barycentres de p points en se bornant au cas p = n + 1 pour reconstituer toute l'enveloppe convexe. Ainsi dans un plan, étant donné A, on construit mentalement son enveloppe convexe en noircissant par la pensée tous les triangles à sommets dans A ; en dimension 3 on utiliserait des tétraèdres, et ainsi de suite.
Le théorème s'énonce précisément ainsi :
Théorème — Dans un espace affine de dimension n, l'enveloppe convexe d'un sous-ensemble A est l'ensemble des combinaisons convexes de familles de n + 1 points de A.
Une fois cet énoncé connu, il est facile d'en déduire un corollaire important :
Corollaire — Dans un espace affine de dimension finie, l'enveloppe convexe d'un compact est compacte.
(Alors que par exemple dans l'espace de Hilbert ℓ2, de base hilbertienne (δn)n∈ℕ, la suite (δn/n)n∈ℕ et sa limite 0 forment un compact, dont l'enveloppe convexe n'est même pas fermée[2].)
Aspects algorithmiques
En 2D
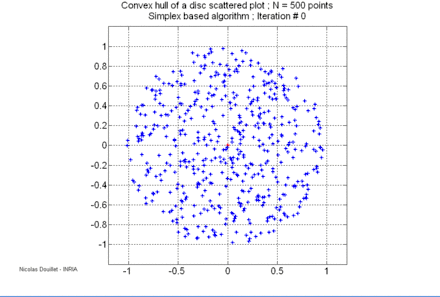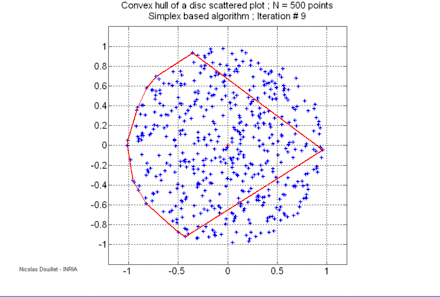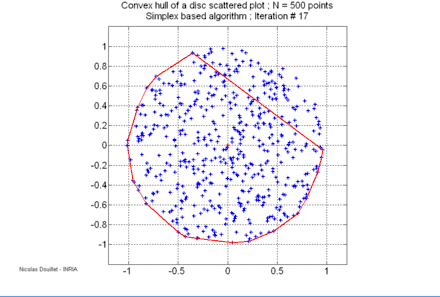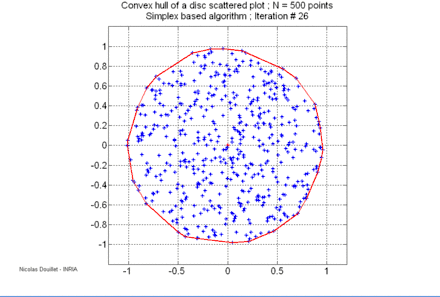
Le calcul de l'enveloppe convexe d'un ensemble de points est un problème classique en géométrie algorithmique. Plusieurs algorithmes ont été inventés pour résoudre ce problème, leur complexité varie :
- marche de Jarvis, en , étant le nombre de points de l'enveloppe convexe ;
- algorithme de Chan, en ;
- parcours de Graham, en ;
- heuristique de Akl-Toussaint ;
- utilisation du diagramme de Voronoï[3], en : les points de l'enveloppe convexe définissent des cellules de Voronoï ouvertes, il suffit de détecter ces cellules et de relier les germes des cellules adjacentes.
Dimensions d'ordres supérieurs
Pour un ensemble fini de points, l'enveloppe convexe est un polyèdre convexe. Cependant, sa représentation n'est pas aussi facile que dans le cas du plan. Pour les dimensions strictement supérieures à 2, même si les arêtes du polyèdre sont connues, la construction des facettes n'est pas une tâche triviale. Un certain nombre d'algorithmes sont quand même connus pour la dimension 3, mais aussi dans le cas général.[réf. nécessaire]
Références
- Marcel Berger, Géométrie [détail des éditions], Prop. 11.1.8.4, tome 3, p. 26 dans l'édition de 1978.
- (en) Charalambos D. Aliprantis et Kim C. Border, Infinite Dimensional Analysis: A Hitchhiker's Guide, Springer, (lire en ligne), p. 185.
- (en) Michael Ian Shamos, Computational Geometry : thèse de doctorat, université Yale,
(en) Michael Ian Shamos et Dan Hoey, « Closest-point problems », dans Proceeding of 16th Annual IEEE Symposium on Foundations of Computer Science, Los Angeles, IEEE Computer Society Press, (lire en ligne), p. 151-162.