Combinaison convexe

Étant donnés trois points ${\displaystyle x_{1},x_{2},x_{3}}$ dans un plan, le point P est une combinaison convexe des trois points, tandis que Q ne l'est pas (Q est seulement une combinaison barycentrique des trois points).

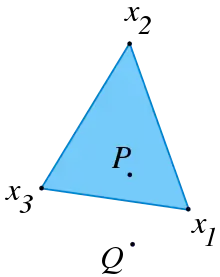
Soit E un espace affine réel (c'est-à-dire que les scalaires sont les nombres réels). Si ${\displaystyle n\in \mathbb {N} ^{*}}$ et ${\displaystyle x_{1},\ldots ,x_{n}}$ sont des points de E, une combinaison convexe des ${\displaystyle x_{i}}$ est[1] un point ${\displaystyle p}$ de la forme

${\displaystyle p=\sum _{i=1}^{n}\lambda _{i}x_{i}~,}$

où ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ sont des réels positifs de somme 1.

Le problème du point extrême consiste à déterminer si un point P₀ est ou non une combinaison convexe de points P_i, 1 ≤ i ≤ n. Dobkin et Reiss[2] ont montré que ce problème avait une complexité linéaire, en O(n), dans ${\displaystyle \mathbb {R} }$ et ${\displaystyle \mathbb {R} ^{2}}$. Megiddo[3] a montré que la complexité était linéaire en dimension finie, dans ${\displaystyle \mathbb {R} ^{d}}$ avec d fini.

La résolution se ramène à savoir s'il existe une droite (dans ${\displaystyle \mathbb {R} ^{2}}$), un plan (dans ${\displaystyle \mathbb {R} ^{3}}$) ou un hyperplan (dans ${\displaystyle \mathbb {R} ^{d}}$, d > 3) passant par P₀, tel que tous les points P_i sont du même côté de la droite, du plan ou de l'hyperplan. Cela revient donc au problème de séparation : séparer un ensemble de points par un hyperplan.

Dans le plan, la recherche peut se faire de la manière suivante[3]. On effectue une transformation affine de sorte que P₀ ait pour coordonnées (0 ; 0) et P₁(0 ; 1) ; de ce fait, la droite de séparation, si elle existe, ne peut pas être l'axe des y. Le point P_i a pour coordonnées (x_i, y_i).

La droite cherchée passe par P₀, l'origine, et a donc pour équation :

y = ax, ce qui s'écrit également si x est non nul y/x = a.

Cette droite délimite deux demi-plans d'équation (y < ax) et (y > ax).

Si P₀ n'est pas dans l'enveloppe convexe, alors tous les points sont dans le même demi plan, c'est-à-dire que tous les points doivent être au-dessus de la droite (puisqu'au moins un point, P₁, l'est). On doit donc avoir pour tout i

y_i > ax_i

soit

• si x_i > 0, alors y_i/x_i > a ;
• si x_i < 0, alors y_i/x_i < a.

On a donc la condition nécessaire et suffisante pour que a existe, c'est-à-dire pour que P₀ soit hors de l'enveloppe convexe :

${\displaystyle \left\{{\begin{aligned}\max\{y_{i}/x_{i}\mid x_{i}<0\}&<\min\{y_{i}/x_{i}\mid x_{i}>0\}\\y_{i}>0&{\text{ si }}x_{i}=0.\end{aligned}}\right.}$

• Calcul de l'enveloppe convexe
• Combinaison barycentrique

• Portail de l'informatique théorique
• Portail des mathématiques