Cercle circonscrit à un triangle

En géométrie du triangle, le cercle circonscrit à un triangle non plat est l'unique cercle passant par ses trois sommets.

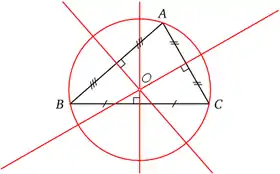
Médiatrices et cercle circonscrit d'un triangle.

Le centre de ce cercle est le point de concours des médiatrices des côtés du triangle.

Propriétés élémentaires

Les trois médiatrices d'un triangle sont concourantes en un point $O$ équidistant des trois sommets (qui est aussi le centre du cercle circonscrit, voir ci-dessous).

Démonstration

Notons $O$ l'intersection des deux médiatrices des segments $[AB]$ et $[AC]$ .

$O$ est sur la médiatrice de $[AB]$ donc $AO = BO$ .
$O$ est sur la médiatrice de $[AC]$ donc $AO = CO$ .

Donc $BO = CO$ : par suite $O$ est sur la médiatrice du segment $[BC]$ . Les trois médiatrices sont donc concourantes en $O$ .

Il existe un et un seul cercle passant à la fois par les trois sommets du triangle. Ce cercle de centre $O$ est appelé cercle circonscrit au triangle.

Démonstration

Existence

Elle a été prouvée ci-dessus : $AO = BO = CO$ , donc le cercle de centre $O$ et passant par A passe aussi par B et C.

Unicité

Si un cercle passe à la fois par A et B, son centre appartient à la médiatrice de $[AB]$ . S'il passe par A et C, son centre appartient à la médiatrice de $[AC]$ . Donc, si un cercle passe par les trois points A, B et C, son centre appartient à la fois aux médiatrices de $[AB]$ et de $[AC]$ , c'est-à-dire à leur intersection. Celle-ci se réduit à un point, $O$ ; le cercle a donc nécessairement pour centre $O$ . Le rayon du cercle est donc égal à $AO$ . On a unicité du centre et du rayon, donc du cercle.

Cercle circonscrit défini par le théorème de l'angle inscrit.

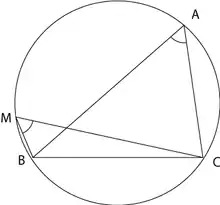
D'après le théorème de l'angle inscrit, le cercle circonscrit au triangle (ABC) est le lieu des points M vérifiant :
$((MB),(MC))=((AB),(AC))\,(1)$
où $(D,D')$ désigne l'angle orienté des droites D et D'. On peut permuter les lettres A,B,C dans la relation (1) , ou l'écrire sous la forme :

((BM),(BA))=((CM),(CA))\,(2)

Il existe une infinité de triangles dont la base est connue et d'angle au sommet opposé connu, et le lieu de ces sommets forme un cercle.

Démonstration

La formule des sinus nous dit que :

{\frac {a}{\sin {\hat {A}}}}=2R

donc le rayon du cercle circonscrit ne dépend que de la longueur de la base a et de l'angle au sommet opposé ${\hat {A}}$ . Il en découle que pour deux points fixes A et B sur un cercle de rayon R et distants de a, tout point C sur ce cercle à l'exception de la coïncidence avec l'un des autres points forme une angle constant ${\widehat {ACB}}$ .

{\widehat {ACB}}=\arcsin {\frac {2R}{a}}

.

Il existe donc bien une infinité de points C tel que l'angle ${\widehat {ACB}}$ soit constant, et le lieu de ces points est un cercle de rayon $R={\frac {a}{2\sin {\hat {A}}}}$ .

Position du centre

Soit $Ω$ le centre du cercle et I le centre de $[AB]$ . $O$ se trouve donc sur la médiatrice de $[AB]$ , et $[AO]$ est un rayon du cercle. On a donc

{AO}^{2}={AI}^{2}+{IO}^{2}

On notera h la distance $I Ω$ .

h^{2}=R^{2}-\left({\frac {a}{2}}\right)^{2}=\left({\frac {a}{2\sin {\hat {A}}}}\right)^{2}-\left({\frac {a}{2}}\right)^{2}

h^{2}=\left({\frac {a}{2}}\right)^{2}\left({\frac {1}{\sin ^{2}{\hat {A}}}}-1\right)=\left({\frac {a}{2}}\right)^{2}\left({\frac {\cos ^{2}{\hat {A}}}{\sin ^{2}{\hat {A}}}}\right)

h={\frac {a}{2\tan {\hat {A}}}}

Le cercle décrit par le sommet C est donc entièrement caractérisé par la longueur de sa base et l'angle au sommet. On peut donc tracer le cercle sans connaitre précisément le point C.

Centre, rayon et équation cartésienne

Centre

On note $O$ le centre du cercle circonscrit, a = BC, b = CA, c = AB les longueur des trois côtés du triangle et ${\hat {A}},{\hat {B}},{\hat {C}}$ les angles opposés respectivement à chacun de ces trois côtés.

Dans le repère barycentrique $(A,B,C)$ , les coordonnées barycentriques du centre $O$ sont $(\sin 2{\hat {A}},\sin 2{\hat {B}},\sin 2{\hat {C}})$ , ou $(a\cos {\hat {A}},b\cos {\hat {B}},c\cos {\hat {C}})$ , ou encore[1] $\left(a^{2}(b^{2}+c^{2}-a^{2}),b^{2}(c^{2}+a^{2}-b^{2}),c^{2}(a^{2}+b^{2}-c^{2})\right)$ .

Ses coordonnées trilinéaires sont $\cos {\hat {A}}:\cos {\hat {B}}:\cos {\hat {C}}$ .

Ses coordonnées cartésiennes dans un repère orthonormé sont, avec $A=(x_{A},y_{A})$ , $B=(x_{B},y_{B})$ , $C=(x_{C},y_{C})$ et $\Delta =2{\begin{vmatrix}x_{A}&y_{A}&1\\x_{B}&y_{B}&1\\x_{C}&y_{C}&1\end{vmatrix}}$ :

x_{O}={\frac {1}{\Delta }}{\begin{vmatrix}x_{A}^{2}+y_{A}^{2}&y_{A}&1\\x_{B}^{2}+y_{B}^{2}&y_{B}&1\\x_{C}^{2}+y_{C}^{2}&y_{C}&1\end{vmatrix}},\qquad y_{O}=-{\frac {1}{\Delta }}{\begin{vmatrix}x_{A}^{2}+y_{A}^{2}&x_{A}&1\\x_{B}^{2}+y_{B}^{2}&x_{B}&1\\x_{C}^{2}+y_{C}^{2}&x_{C}&1\end{vmatrix}}

.

(On le démontre en identifiant les coefficients dans les deux équations cartésiennes équivalentes ci-dessous.)

Rayon

Son rayon $R$ peut s'exprimer grâce à la loi des sinus :

{\frac {a}{\sin {\hat {A}}}}={\frac {b}{\sin {\hat {B}}}}={\frac {c}{\sin {\hat {C}}}}={\frac {abc}{2S}}=2R

où S désigne l'aire du triangle.

On en déduit les expressions symétriques : $R={\frac {p}{\sin {\hat {A}}+\sin {\hat {B}}+\sin {\hat {C}}}}$ où $p = a + b + c / 2$ est le demi-périmètre du triangle et $R^{2}={S \over {2\sin {\hat {A}}\sin {\hat {B}}\sin {\hat {C}}}}$ .

Compte tenu de la formule de Héron, on a : $R={abc \over {4{\sqrt {p(p-a)(p-b)(p-c)}}}}$ .

La relation d'Euler donne la distance $d$ du centre du cercle circonscrit au centre du cercle inscrit, soit $d 2 = R 2 - 2 Rr$ (où $r$ est le rayon du cercle inscrit)[2].

Équation cartésienne

Dans le plan euclidien, il est possible de donner l'équation cartésienne du cercle circonscrit au triangle.

Le cercle circonscrit est l'ensemble des points $M=(x,y)$ tels que $\left\|{\overrightarrow {OM}}\right\|^{2}=R^{2}$ avec $O$ et $R$ comme ci-dessus, soit

(x-x_{O})^{2}+(y-y_{O})^{2}=R^{2}

.

Mais on peut aussi écrire directement cette équation cartésienne (sans calculer au préalable $x_{O}$ , $y_{O}$ et $R$ ).

Première écriture, par un déterminant

L'équation cartésienne du cercle circonscrit s'écrit :

{\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{A}^{2}+y_{A}^{2}&x_{A}&y_{A}&1\\x_{B}^{2}+y_{B}^{2}&x_{B}&y_{B}&1\\x_{C}^{2}+y_{C}^{2}&x_{C}&y_{C}&1\end{vmatrix}}=0

.

Démonstration

L'équation d'un cercle dans un repère orthonormé est de la forme $x^{2}+y^{2}+\alpha x+\beta y+\gamma =0$ . Les quatre points $M,A,B,C$ sont donc cocycliques si et seulement s'il existe trois constantes $\alpha ,\beta ,\gamma$ telles que :

{\begin{cases}x^{2}+y^{2}+\alpha x+\beta y+\gamma &=0\\x_{A}^{2}+y_{A}^{2}+\alpha x_{A}+\beta y_{A}+\gamma &=0\\x_{B}^{2}+y_{B}^{2}+\alpha x_{B}+\beta y_{B}+\gamma &=0\\x_{C}^{2}+y_{C}^{2}+\alpha x_{C}+\beta y_{C}+\gamma &=0\\\end{cases}}

.

L'existence d'un tel triplet de constantes équivaut à l'existence, dans le noyau de la matrice $N:={\begin{pmatrix}x^{2}+y^{2}&x&y&1\\x_{A}^{2}+y_{A}^{2}&x_{A}&y_{A}&1\\x_{B}^{2}+y_{B}^{2}&x_{B}&y_{B}&1\\x_{C}^{2}+y_{C}^{2}&x_{C}&y_{C}&1\end{pmatrix}}$ , d'un vecteur dont la première composante est $1$ .

Comme les trois points $A,B,C$ sont supposés non alignés, le mineur ${\begin{vmatrix}x_{A}&y_{A}&1\\x_{B}&y_{B}&1\\x_{C}&y_{C}&1\end{vmatrix}}$ est non nul, si bien que la condition précédente équivaut simplement à $\ker N\neq \{0\}$ donc à $\det N=0$ .

Deuxième écriture, complexe

Si $a,b,c,z$ sont les affixes respectives de $A,B,C,M$ , l'équation cartésienne du cercle circonscrit s’obtient en écrivant la nullité de la partie imaginaire de

(z-b)({\overline {z}}-{\overline {c}})(a-c)({\overline {a}}-{\overline {b}})

Démonstration

La condition angulaire ci-dessus $((MB),(MC))=((AB),(AC))$ s'écrit en complexes $\arg \left({\frac {z-b}{z-c}}\right)=\arg \left({\frac {a-b}{a-c}}\right)\mod \pi$

D'où en utilisant le birapport, la condition équivalente :

[a,b,c,z]=\left({\frac {z-b}{z-c}}\right):\left({\frac {a-b}{a-c}}\right)

réel

En multipliant par les conjugués des dénominateurs, on obtient bien la condition

\Im {((z-b)({\overline {z}}-{\overline {c}})(a-c)({\overline {a}}-{\overline {b}}))}=0

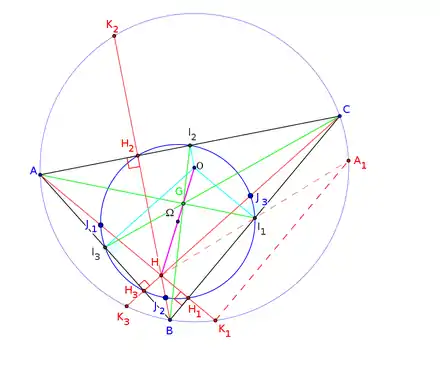
Points remarquables appartenant au cercle circonscrit à un triangle

Appartiennent au cercle circonscrit au triangle :

les symétriques de l'orthocentre par rapport aux côtés ;

Démonstration

L'homothétie de centre H et de rapport $1 / 2$ , transforme A₁ (symétrique de A par rapport à $Ω$ ) en I₁, de même les points I₂ et I₃ sont les images de deux points du cercle circonscrit. Le cercle d'Euler circonscrit au triangle I₁I₂I₃ est l'image du cercle circonscrit à ABC, dans l'homothétie de centre H et de rapport $1 / 2$ .

On note K₁, le point d'intersection (autre que A) de la hauteur (AH₁) avec le cercle circonscrit. Le segment [AA₁] étant un diamètre, le triangle AK₁A₁, inscrit dans un demi-cercle, est rectangle. Les droites (BC) et (K₁A₁), perpendiculaires à la hauteur (AH₁), sont parallèles. La droite (I₁H₁) passe par le milieu I₁ de [HA₁], c'est la droite des milieux de HA₁K₁, H₁ est donc milieu de [HK₁]. La droite (HK₁) étant perpendiculaire à (BC), K₁ est le symétrique de H par rapport à (BC).

Cercle et droite d'Euler.

les symétriques de l'orthocentre par rapport aux milieux des côtés ;

Démonstration

Notons I₁ le milieu de [BC], I₂ le milieu de [AC] et I₃ le milieu de [AB]. Il n'est pas difficile de voir que l'homothétie de centre G et de rapport $- 1 / 2$ transforme le triangle ABC en le triangle médian I₁I₂I₃ et le cercle circonscrit de ABC en cercle circonscrit à I₁I₂I₃ : ce dernier cercle est précisément le cercle d'Euler.

Cette même homothétie de centre G permet de dire que ${\overrightarrow {OI_{1}}}=-{\frac {1}{2}}{\overrightarrow {HA}}={\frac {1}{2}}{\overrightarrow {AH}}$ . Soit A₁ le symétrique de A par rapport à O. Dans le triangle AHA₁, la droite (OI₁) est donc la droite des milieux du triangle et le point I₁ le milieu de [HA₁] : A₁ est le symétrique de H par rapport à I₁.

Cercle et droite d'Euler.

les milieux des segments joignant les centres des cercles exinscrits au triangle ;
les milieux des segments joignant le centre du cercle inscrit et le centre des cercles exinscrits au triangle.

Démonstration

Le cercle circonscrit au triangle est le cercle d'Euler du triangle formé par les centres des cercles exinscrits (Triangle de Bevan). Les sommets du triangle sont les pieds des hauteurs du triangle de Bevan associé. Ainsi, ledit cercle passe également par les milieux des côtés du triangle de Bevan (qui sont les centres des cercles exinscrits au triangle originel) et les milieux des segments joignant l'orthocentre du triangle de Bevan (le centre du cercle inscrit du triangle originel) et les sommets du triangle de Bevan (les milieux des segments joignant le centre du cercle inscrit et le centre des cercles exinscrits au triangle originel).

Références

(en) Eric W. Weisstein, « Barycentric Coordinates », sur MathWorld.
« Distance OI », sur geogebra.org.

Articles connexes

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Eric W. Weisstein, « Barycentric Coordinates », sur MathWorld.

[2] « Distance OI », sur geogebra.org.