Spectroscopie de rayons X à dispersion d'énergie

Principe du détecteur à l'état solide

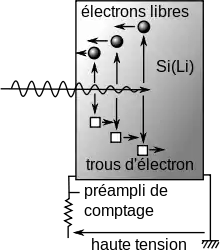
Les photons X sont captés par un détecteur à l'état solide, un semi-conducteur de silicium dopé au lithium (on parle de détecteur Si(Li)) ou un détecteur à dérive en silicium (drift silicon detector, SDD), refroidi à l'azote liquide ou par effet Peltier. Les photons X provoquent des ionisations dans le semiconducteur, les paires électrons-trous libres migrent sous l'effet du champ électrique de polarisation et provoquent des impulsions de courant dont la hauteur est proportionnelle à l'énergie du photon. On peut séparer par un discrimineur les impulsions selon leur hauteur, et donc compter les photons incidents selon leur énergie.

Ce type de détecteur a une bonne sensibilité pour les photons ayant une énergie entre 0.2 et 20 keV ; on détecte les éléments à partir du bore (Z = 5), mais le rendement est très faible car les photons de bore sont absorbés par la fenêtre qui protège le détecteur. Le carbone (Z = 6) est bien détecté.

La principale limitation de ce système d'analyse chimique provient de la largeur des raies, qui est importante (la résolution du système est de 130 eV sur le pic du manganèse, ce qui correspond à 60 eV sur le carbone), les pics de l'azote et de l'oxygène (énergie respective des raies Kα₁ : 0,40 keV et 0,53 keV) ne sont pas totalement séparés. Mais la complexité des spectres augmente surtout lorsque des raies d'une autre transition se superposent, par ex. la série de raies L du chrome et les raies K de l'oxygène. En revanche, l'analyse est très rapide, en effet, le signal est collecté sur plusieurs canaux à la fois (typiquement 1024 ou 2048 canaux, un canal correspondant à division de l'échelle d'énergie, par exemple 10 ou 20 eV) : on analyse toutes les énergies en même temps. Le temps d'acquisition va de quelques secondes à la minute.

Le nombre d'impulsions pour chaque canal est appelé « nombre de coups », on utilise aussi fréquemment le taux de comptage exprimé en « coups par seconde » (cps). Le nombre de coups est proportionnel au nombre de photons passant par le détecteur.

Tension dans un détecteur avec remise à zéro périodique

Le détecteur se comporte comme un condensateur qui se charge à chaque arrivée de photon. Soit il est remis à zéro régulièrement (comme dans l'illustration ci-après), soit le circuit permet un « courant de fuite », le condensateur se décharge au fur et à mesure.

Filtrage numérique du signal

Ce signal doit ensuite être traité. Auparavant, on utilisait des circuits analogiques, maintenant, le signal est collecté tel quel et analysé numériquement. Il est tout d'abord filtré ; en général, on calcule la moyenne du signal sur un intervalle de largeur δt₁, et on remplace le point médian de l'intervalle par cette moyenne. Puis il est dérivé : on calcule simplement (V(t) - V(t-δt₂))/δt₂.

Influence des paramètres de filtrage

Ceci génère des pics trapézoïdaux, ayant deux caractéristiques :

• le temps de montée, et
• la largeur du plateau.

Ces deux caractéristiques dépendent de δt₁ et de δt₂, et conditionnent la détection des photons :

• plus on filtre (δt₁ et δt₂ élevés), mieux on peut déterminer la hauteur des pics avec précision (bon rapport signal/bruit)
• mais plus les pics sont larges, on est alors confronté au phénomène d'empilement (pile-up) qui fait que l'on peut ne pas détecter tous les pics (on augmente le temps mort).

Une autre approche purement numérique est employée: l'énergie du photon qui vient d'arriver est directement proportionnelle à la hauteur de la marche. Il suffit donc de mesurer cette différence et s'assurer que le signal est bien pris sur un palier de part et d'autre de la marche. Pour ceci, la sortie du préamplificateur est numérisée à haute fréquence : 10 GHz. Pour améliorer la précision de la mesure, les valeurs mesurées sont moyennées pendant des durées de 8 à 256 ms selon la « constante de temps » choisie. Un circuit en parallèle détecte l'arrivée du photon pour savoir où se trouve la « marche ». Si un photon arrive avant la fin du temps d'intégration, l'information est rejetée et contribue au temps mort. Cette approche fournit une très grande linéarité du signal.

Les photons d'une raie ayant tous la même énergie, la raie devrait figurer comme un « bâton » sur le spectre. Toutefois, en raison des imperfections des appareils, elles figurent sous la forme d'un pic ayant une forme de cloche (profil globalement gaussien). Certains photons de la raie sont donc détectés pour des hauteurs d'impulsion légèrement différentes de la théorie ; pour prendre tous les photons en compte, il faut donc considérer la surface nette du pic (partie de la surface au-dessus du fond). Par ailleurs, certains photons détectés proviennent d'autres phénomènes (essentiellement diffusion Rayleigh et diffusion Compton du rayonnement du tube, et probablement Bremsstrahlung des photoélectrons), ce qui forme le fond continu (le terme "bruit de fond" étant injustement utilisé).

Il faut donc déterminer la surface nette, c'est-à-dire la surface au-dessus de la ligne de bruit de fond, pour déterminer l'intensité.

Dans le cas de l'analyse dispersive en énergie, la forme du pic n'est pas constante, plus un pic est haut, plus il est large. On ne peut donc pas, comme en analyse dispersive en longueur d'onde, se contenter de mesurer la hauteur. De ce fait, cette méthode est plus sensible aux problèmes de superposition de pic (interférences entre les raies), et ce d'autant plus que les pics sont larges.

On peut utiliser des méthodes mathématiques de déconvolution pour séparer les pics, ou plus précisément de simulation de spectre : on simule un spectre à partir d'un échantillon fictif ayant des concentrations a priori, et on ajuste les concentrations afin que le spectre simulé soit le plus proche possible du spectre mesuré. Cette démarche s'approche de la méthode de Rietveld utilisée en diffraction de rayons X.