Variables aléatoires continues/Loi normale

Présentation

La loi normale est la loi de probabilité continue la plus connue. Nous avons amorcé son étude au niveau 13, au chapitre 4 de la leçon sur les lois de probabilité continues.

On la retrouve dans de nombreuses situations concrètes, et aussi dans de nombreux résultats théoriques.

Sa densité de probabilité est la célèbre « courbe en cloche » de Gauss.

Définition

La loi normale est une loi de probabilité pour les variables aléatoires continues.

On la définit au moyen d'une densité de probabilité (voir chap. 1) :

Définition

La densité de probabilité d'une variable aléatoire continue suivant une loi normale ${\mathcal {N}}(\mu ,\sigma ^{2})$ (dite aussi loi de Laplace-Gauss) est :

f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\mathrm {e} ^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}

.

Remarques

Le fait que cette fonction est bien une densité de probabilité sur $\mathbb {R}$ se déduit de la valeur de l'intégrale de Gauss : $\int _{\mathbb {R} }\mathrm {e} ^{-u^{2}}\mathrm {d} u={\sqrt {\pi }}$ .
Nous démontrerons plus loin que les paramètres $\mu$ et $\sigma$ sont respectivement égaux à l'espérance et à l'écart-type de la loi normale ${\mathcal {N}}(\mu ,\sigma ^{2})$ .
La notation ${\mathcal {N}}(\mu ,\sigma )$ peut aussi être rencontrée. Il faut donc faire attention à la valeur (variance $\sigma ^{2}$ ou écart-type $\sigma$ ) considérée comme deuxième paramètre.

Courbes en cloche

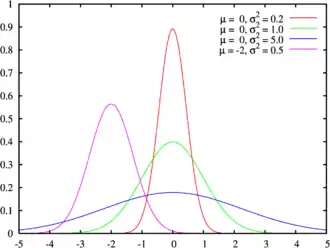
Exemples de densités gaussiennes pour différentes valeurs des paramètres.

On observe la forme « en cloche », que l’on peut observer en statistiques quand on construit l'histogramme d'un caractère dépendant d'un grand nombre de données :

la taille d'un individu (dépend de la taille de ses parents, de son alimentation, de son mode de vie…) ;
la conformité d'une pièce technologique ;
etc.

Loi normale centrée réduite

Définition

La loi normale centrée réduite est celle dont l'espérance vaut 0 (centrée) et l'écart-type 1 (réduite), c'est-à-dire ${\mathcal {N}}(0,1)$ . Sa densité est :

f(t)={\frac {1}{\sqrt {2\pi }}}\,\mathrm {e} ^{-{\frac {t^{2}}{2}}}

.

Un simple changement de variable dans le calcul de la fonction de répartition montre que :

Propriété

$X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ si et seulement si ${\frac {X-\mu }{\sigma }}\sim {\mathcal {N}}(0,1)$ .

Moments

Fonction génératrice des moments

Théorème

La fonction génératrice des moments d'une variable aléatoire $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ est :

M_{X}(t):=\mathbb {E} \left(\mathrm {e} ^{tX}\right)=\exp \left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)

.

Démonstration

Effectuons le changement de variable $x=y+\sigma ^{2}t$ :

{\begin{aligned}\mathbb {E} \left(\mathrm {e} ^{tX}\right)&={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }\exp \left(tx-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} x\\&={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }\exp \left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}-{\frac {(y-\mu )^{2}}{2\sigma ^{2}}}\right)\,\mathrm {d} y\\&=\exp \left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right){\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{+\infty }\mathrm {e} ^{-{\frac {1}{2}}\left({\frac {y-\mu }{\sigma }}\right)^{2}}\,\mathrm {d} y\\&=\exp \left(\mu t+{\frac {\sigma ^{2}t^{2}}{2}}\right)\end{aligned}}

Remarque

Ceci prouve au passage que $X$ a des moments à tout ordre.

Espérance et formule de récurrence

Proposition

Soit $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ .

L'espérance de $X$ est égale à $\mu$ :
$\mathbb {E} (X)=\mu$ .
Les moments de $X$ vérifient la relation de récurrence :
$\forall n\geq 1\quad \mathbb {E} (X^{n+1})=\mu \mathbb {E} (X^{n})+n\sigma ^{2}\mathbb {E} (X^{n-1})$ .

Démonstration

D'après la proposition précédente, $M'_{X}(t)=\left(\mu +t\sigma ^{2}\right)M_{X}(t)$ donc

\sum _{n\geq 0}\mathbb {E} (X^{n+1}){\frac {t^{n}}{n!}}=M'_{X}(t)=\left(\mu +t\sigma ^{2}\right)\sum _{n\geq 0}\mathbb {E} (X^{n}){\frac {t^{n}}{n!}}=\mu +\sum _{n\geq 1}\left(\mu \mathbb {E} (X^{n})+n\sigma ^{2}\mathbb {E} (X^{n-1})\right){\frac {t^{n}}{n!}}

.

Variance et autres moments centrés

Si $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ alors $X-\mathbb {E} (X)=X-\mu \sim {\mathcal {N}}(0,\sigma ^{2})$ . Par conséquent :

Proposition

Soit $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ .

La fonction génératrice des moments centrés de $X$ est :

\mathbb {E} \left(\mathrm {e} ^{t(X-\mu )}\right)=\exp \left({\frac {\sigma ^{2}t^{2}}{2}}\right)

.

Autrement dit : les moments centrés d'ordres impairs sont nuls et ceux d'ordres pairs sont donnés par :

\mathbb {E} \left((X-\mu )^{2n}\right)={\frac {(2n)!}{2^{n}n!}}\sigma ^{2n}

.

Corollaire

La variance et l'écart-type d'une variable aléatoire $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ sont :
$\mathrm {V} (X)=\sigma ^{2},\quad \sigma (X)=\sigma$ .
Le coefficient d'asymétrie d'une loi normale est nul.
Le kurtosis d'une loi normale vaut 3.

Cette valeur est significative : si $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ alors $\mathbb {P} (-3\sigma \leq X-\mu \leq 3\sigma )\approx 0{,}997$ .

Souvent, on normalise le kurtosis d'une loi en lui soustrayant 3.

Table de probabilité

Dans les applications calculatoires, on se ramène à la table de probabilité de la loi normale centrée réduite.

Dans ce tableau, pour $T\sim {\mathcal {N}}(0,1)$ , on donne $\mathbb {P} (T\leq a)$ pour $a\in [0{,}00,\,3{,}99]$ .

L'entrée en lignes représente les chiffres des unités et des dixièmes de $a$ et l'entrée en colonnes représente le chiffre des centièmes de $a$ .

Exemples

Si T suit une loi normale centrée réduite, déterminer à l'aide de la table la probabilité que T soit inférieure ou égale à 1,00.

Solution

On trouve dans la table 84134.

thumr

On en déduit que la probabilité cherchée est de 0,84134.

Si X suit une loi normale d'espérance 1 et d'écart-type 2, déterminer la probabilité pour que $X\leq 3$ .

Solution

X\leq 3\Leftrightarrow X-1\leq \Leftrightarrow T:={\frac {X-1}{2}}\leq 1

.

Or, d’après le théorème de changement de variable, T suit une loi centrée réduite. Donc

\mathbb {P} (T\leq 1)=0{,}84134

d'après l'exemple précédent. Finalement,

\mathbb {P} (X\leq 3)=0{,}84134

.

Une entreprise produit des boules, dont le diamètre d (en millimètres) suit une loi ${\mathcal {N}}\left(73,\sigma ^{2}\right)$ . Une boule sera dite « conforme » si $72{,}7\leq d\leq 73{,}3$ .

On suppose que $\sigma =0{,}2$ . Calculer la probabilité qu'une boule soit conforme.
Quelle valeur devrait prendre $\sigma$ pour que la probabilité d'obtenir une boule conforme soit supérieure à 0,9 ?

Solution

$72{,}7\leq d\leq 73{,}3\Leftrightarrow -1{,}5\leq {\frac {d-73}{0{,}2}}\leq 1{,}5$ , or $X:={\frac {d-73}{0{,}2}}\sim {\mathcal {N}}(0,1)$ .
La table donne $\mathbb {P} (X\leq 1{,}5)\approx 0{,}93319$ , or $\mathbb {P} (X\leq -1{,}5)=1-\mathbb {P} (X\leq 1{,}5)$ donc
$\mathbb {P} (72{,}7\leq d\leq 73{,}3)=\mathbb {P} (-1{,}5\leq X\leq 1{,}5)=2\mathbb {P} (X\leq 1{,}5)-1\approx 2\times 0{,}43319=0{,}86638$ .
$72{,}7\leq d\leq 73{,}3\Leftrightarrow -{\frac {0{,}3}{\sigma }}\leq {\frac {d-73}{\sigma }}\leq {\frac {0{,}3}{\sigma }}$ , or $Y:={\frac {d-73}{\sigma }}\sim {\mathcal {N}}(0,1)$ .
$2\mathbb {P} \left(Y\leq {\frac {0{,}3}{\sigma }}\right)-1>0{,}9\Leftrightarrow \mathbb {P} \left(Y\leq {\frac {0{,}3}{\sigma }}\right)>0{,}95\Leftrightarrow$ (d'après la table) ${\frac {0{,}3}{\sigma }}\geq 1{,}65\Leftrightarrow \sigma \leq {\frac {0{,}3}{1{,}65}}\approx 0{,}182$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.