Soit ${\displaystyle \sigma }$ un nombre réel strictement positif et ${\displaystyle \mu }$ un nombre réel quelconque. On appelle loi normale ou loi de Gauss ou loi de Laplace-Gauss de paramètres ${\displaystyle \mu }$ et ${\displaystyle \sigma }$, la loi de probabilité dont la densité est définie par :

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\mathrm {e} ^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$.

Nous l'étudierons plus en détail au niveau 14, au chapitre 3 de la leçon sur les variables aléatoires continues.

Nous admettons ici que cette fonction (continue, positive) est bien une densité de probabilité, c'est-à-dire que ${\displaystyle \lim _{a\to -\infty \atop b\to +\infty }\int _{a}^{b}f(x)\,\mathrm {d} x=1}$.

Cette loi est utilisée pour les variables aléatoires dont la valeur dépend d'un grand nombre de causes indépendantes dont les effets s'additionnent et dont aucune n'est prépondérante.

Espérance mathématique et écart-type

Proposition

L'espérance d'une variable aléatoire suivant une loi normale de paramètres ${\displaystyle \mu }$ et ${\displaystyle \sigma }$ est égale au paramètre ${\displaystyle \mu }$.

${\displaystyle E(X)=\mu }$.

On montre aussi (admis) que l'écart-type est égal à ${\displaystyle \sigma }$.

Loi normale centrée réduite

La loi normale d'espérance ${\displaystyle \mu =0}$ et d'écart-type ${\displaystyle \sigma =1}$ est appelée la loi normale centrée réduite.

Loi normale centrée réduite

On appelle loi normale centrée réduite, la loi de probabilité dont la densité est donnée par :

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi }}}\mathrm {e} ^{-{\frac {x^{2}}{2}}}}$.

Graphe de ${\displaystyle f}$.

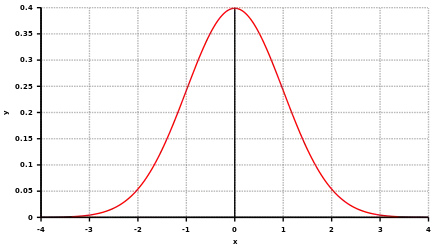
Relation entre loi normale et loi normale centrée réduite

La loi normale dans le cas le plus général, c'est-à-dire dont la fonction densité de probabilité est :

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$,

n'est pas facile à étudier du fait que l'on ne connait pas la primitive de la fonction ${\displaystyle f}$. Heureusement, on se ramène très facilement à une loi normale centrée réduite en faisant le changement de variable :

${\displaystyle T={\frac {X-\mu }{\sigma }}}$.

On a, en effet, la propriété suivante :

Propriété

Soit ${\displaystyle X}$ une variable aléatoire suivant une loi normale d'espérance ${\displaystyle \mu }$ et d'écart-type ${\displaystyle \sigma }$, alors la variable aléatoire ${\displaystyle T}$ définie par :

${\displaystyle T={\frac {X-\mu }{\sigma }}}$

suit une loi normale centrée réduite.

Cette propriété permet de simplifier l'étude d'une loi normale quelconque en la ramenant à une loi normale centrée réduite. Par exemple, à l'époque où les calculatrices n'existaient pas, on pouvait se contenter de tables sur la loi normale centrée réduite pour pouvoir étudier des phénomènes suivant une loi normale quelconque.

Théorème de Moivre-Laplace

Nous avons le théorème suivant :

Théorème de Moivre-Laplace

Soit ${\displaystyle X_{n}}$ une variable aléatoire suivant une loi binomiale ${\displaystyle {\mathcal {B}}(n;\,p)}$. Soit ${\displaystyle Z_{n}}$ une autre variable aléatoire définie en fonction de ${\displaystyle X_{n}}$ par la relation :

${\displaystyle Z_{n}={\frac {X_{n}-np}{\sqrt {np(1-p)}}}}$.

Alors, pour tous réels ${\displaystyle a}$ et ${\displaystyle b}$, nous avons :

${\displaystyle \lim _{n\to \infty }P(a\leqslant Z_{n}\leqslant b)=\int _{a}^{b}{\frac {1}{\sqrt {2\pi }}}\mathrm {e} ^{-{\frac {t^{2}}{2}}}\,\mathrm {d} t}$.

Le changement de variable aléatoire :

${\displaystyle Z_{n}={\frac {X_{n}-np}{\sqrt {np(1-p)}}}}$

est à rapprocher du changement de variable aléatoire :

${\displaystyle T={\frac {X-\mu }{\sigma }}}$

vu au paragraphe précédent puisque pour une loi binomiale ${\displaystyle {\mathcal {B}}(n;\,p)}$, l'espérance ${\displaystyle \mu }$ et l'écart-type ${\displaystyle \sigma }$ sont donnés par :

Le théorème précédent nous montre donc que la loi normale peut être vue comme la limite d'une loi binomiale lorsque n tend vers ${\displaystyle +\infty }$. Ceci est une propriété appréciable dans la mesure où la loi binomiale est d'autant plus difficile à calculer que la valeur de n est élevée.

Intervalles symétriques

La loi normale exprime comment fluctue une variable aléatoire autour d'une valeur moyenne ${\displaystyle \mu }$. Nous sommes alors intéressés par la probabilité qu'a la variable aléatoire de sortir d'un intervalle symétrique par rapport à cette valeur ${\displaystyle \mu }$.

Soit ${\displaystyle X}$ une variable aléatoire suivant une loi normale centrée réduite. Soit ${\displaystyle \alpha }$ un réel compris entre ${\displaystyle 0}$ et ${\displaystyle 1}$ (exprimant une probabilité). Il existe un unique réel positif ${\displaystyle u_{\alpha }}$ tel que :

${\displaystyle P(-u_{\alpha }\leqslant X\leqslant u_{\alpha })=1-\alpha }$.

Autrement dit ${\displaystyle \alpha }$ exprime la probabilité de sortir d'un intervalle ${\displaystyle [-u_{\alpha },\,u_{\alpha }]}$, symétrique par rapport à l'origine.

Nous connaissons en général par cœur les deux valeurs suivantes :

• ${\displaystyle u_{0{,}05}\simeq 1{,}96}$ ;
• ${\displaystyle u_{0{,}01}\simeq 2{,}58}$.

Nous retrouverons cette notion d'intervalle symétrique par rapport à une valeur donnée dans l'étude sur l'échantillonnage et l'estimation.