Variables aléatoires continues/Définitions

Variable aléatoire continue

Quand le résultat d'une expérience aléatoire n’est pas un entier et n'appartient pas à un ensemble fini,

le mieux est de définir la variable aléatoire correspondante directement sur $\mathbb {R}$ ou sur un intervalle de $\mathbb {R}$ .

Définition

Une variable aléatoire continue $X$ est une fonction qui associe à chaque résultat d'une expérience aléatoire un nombre réel.

On note :

X:\Omega \to \mathbb {R}

.

Remarques

Dans ce cours tourné vers les applications et destiné à des étudiants n'ayant pas abordé la théorie de l'intégration de Lebesgue, nous laisserons de côté les difficultés techniques liées à la définition des ensembles boréliens et des fonctions mesurables.
Le terme « variable aléatoire continue » en probabilités n’est pas synonyme de « fonction continue » en analyse, même si l’idée de départ est similaire. Il s'agit réellement d'un autre concept.

Exemple

On considère une variable aléatoire $X$ prenant une valeur aléatoire entre 0 et 1,

et ce de manière uniforme (cette v.a. est similaire au générateur de nombres pseudo-aléatoires d'une calculatrice).

Toutes les valeurs de [0, 1] ont la même probabilité d’être obtenues.

Mais quelle est alors cette probabilité ?

Solution

Si $x$ appartient à [0, 1], alors $\mathbb {P} (X=x)=0$ . En effet comme il y a une infinité de nombres entre 0 et 1, ils se partagent une probabilité de 1 en une infinité de possibilités. Si elles ont toutes la même probabilité, elles doivent donc avoir une probabilité nulle.
On constate que l’on ne peut pas définir de manière satisfaisante la loi de probabilité d'une v.a. continue en fixant $\mathbb {P} (X=x)$ . La notion de fonction de répartition permet de le faire.

Fonction de répartition

Définition

On appelle fonction de répartition d'une v.a. continue X la fonction F définie sur $\mathbb {R}$ par :

F(x)=\mathbb {P} (X\leq x)

.

Propriétés

Comme une probabilité est toujours inférieure ou égale à 1, on a $F(x)\leq 1$ .
Si on englobe toujours plus de valeurs de $\mathbb {R}$ dans le calcul, la probabilité augmente et tend vers 1.
De même, si on englobe de moins en moins de valeurs de $\mathbb {R}$ , la probabilité tend vers 0.

En résumé :

Proposition

$F$ est croissante.
$\lim _{+\infty }F=1$ .
$\lim _{-\infty }F=0$ .

Finalement, on admettra sans démonstration que F est continue à droite, et que si la variable aléatoire X ne se concentre pas sur des valeurs spécifiques de $\mathbb {R}$ , alors F est continue.
Une fonction de répartition a typiquement cette allure-là :

Exemple

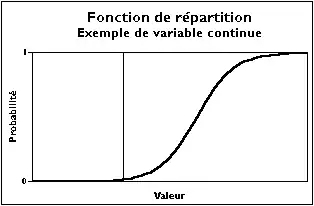
Reprenons l'exemple de la loi uniforme sur [0, 1]. Alors :

F(x)={\begin{cases}0&{\text{si }}x<0\\x&{\text{si }}0\leq x\leq 1\\1&{\text{si }}x>1.\end{cases}}

On constate que cette fonction vérifie les propriétés ci-dessus.

Densité de probabilité

Définition

En général, la fonction de répartition F d'une variable aléatoire X continue (au sens probabiliste)

est continue (au sens analytique) et dérivable par morceaux.

Sa dérivée

f=F'

est appelée densité de probabilité de X.

Propriétés d'une densité de probabilités

Propriété

La densité de probabilité f est positive car F est croissante.
$\int _{-\infty }^{+\infty }f(x)\,\mathrm {d} x=1$ .
$\int _{-\infty }^{a}f(x)\,\mathrm {d} x=\mathbb {P} (X\leq a)=F(a)$ .

Une densité de probabilité a en général cette allure :

Exemple

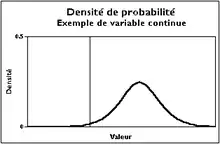
Reprenons l'exemple de la loi uniforme sur [0, 1]. Alors, en dérivant F, on obtient :

f(x)={\begin{cases}0&{\text{ si }}x<0,\\1&{\text{ si }}0<x<1,\\0&{\text{ si }}1<x.\end{cases}}

On constate que cette fonction $f$ vérifie les propriétés ci-dessus.

Espérance, variance, moments

Espérance

Définition

L'espérance d'une variable aléatoire continue possédant une densité

est définie par analogie avec les variables discrètes comme :

\mathbb {E} (X)=\int _{-\infty }^{+\infty }x\ f(x)\,\mathrm {d} x

(sous réserve d'existence, c'est-à-dire ici d'intégrabilité).

Exemple

Reprenons l'exemple de la loi uniforme sur [0, 1]. Alors :

\mathbb {E} (X)=\int _{-\infty }^{+\infty }xf(x)\,\mathrm {d} x=0+\int _{0}^{1}x\,\mathrm {d} x+0={\frac {1}{2}}

.

La v. a. X vaut en moyenne ${\frac {1}{2}}$ .

Variance et écart-type

Définition

La variance d'une variable aléatoire continue possédant une densité f est définie par analogie avec les variables discrètes comme :

\mathrm {V} (X)=\int _{-\infty }^{+\infty }(x-\mathbb {E} (X))^{2}\ f(x)\,\mathrm {d} x

.

Formule

Le calcul de la variance est plus facile avec la formule suivante :

Théorème de König-Huygens

\mathrm {V} (X)=\int _{-\infty }^{+\infty }x^{2}\ f(x)\ dx-\mathbb {E} (X)^{2}=\mathbb {E} (X^{2})-\mathbb {E} (X)^{2}

Démonstration

Il suffit d'appliquer la propriété de linéarité de l'espérance :

\mathrm {V} (X)=\mathbb {E} [(X-\mathbb {E} (X))^{2}]=\mathbb {E} [X^{2}-2\mathbb {E} (X)X+\mathbb {E} (X)^{2}]=\mathbb {E} (X^{2})-2\mathbb {E} (X)\mathbb {E} (X)+\mathbb {E} (X)^{2}\mathbb {E} (1)=\mathbb {E} (X^{2})-\mathbb {E} (X)^{2}

.

Écart-type

Définition

L'écart-type d'une variable aléatoire continue est défini par :

\sigma (X)={\sqrt {\mathrm {V} (X)}}

.

Exemple

Reprenons l'exemple de la loi uniforme sur [0, 1]. Alors :

\mathrm {V} (X)=\int _{-\infty }^{+\infty }x^{2}f(x)\,\mathrm {d} x-\left({\frac {1}{2}}\right)^{2}=0+\int _{0}^{1}x^{2}\,\mathrm {d} x+0-{\frac {1}{4}}={\frac {1}{3}}-{\frac {1}{4}}={\frac {1}{12}}

et

\sigma ={\sqrt {\frac {1}{12}}}={\frac {1}{2{\sqrt {3}}}}

.

Autres moments

Deux autres moments, bien entendu sous réserve d'existence, sont parfois considérés pour affiner la prévision du comportement d'une variable aléatoire :

Le coefficient d'asymétrie $\gamma _{1}=\mathbb {E} \left({\frac {(X-\mathbb {E} (X))^{3}}{\sigma ^{3}}}\right)={\frac {\mu _{3}}{\mu _{2}^{3/2}}}$ permet, selon le signe, de prédire où se trouve l'étalement de la distribution par rapport à l'espérance, soit si la décroissance de la fonction de densité est plus forte à gauche ou à droite.
Le kurtosis $\gamma _{2}=\mathbb {E} \left({\frac {(X-\mathbb {E} (X))^{4}}{\sigma ^{4}}}\right)={\frac {\mu _{4}}{\mu _{2}^{2}}}$ donne une mesure de l'aplatissement de la densité, c'est-à-dire qu’il permet de prédire si la mesure est fortement concentrée autour de l'espérance ou non.

Fonction génératrice des moments

Cette fonction permet de regrouper le calcul de l'intégralité des moments d'une loi, s'ils existent.

Fonction génératrice des moments

Si X est une variable aléatoire qui admet pour fonction de densité $f_{X}$ , on appelle la fonction génératrice des moments :

$M_{X}(t)=\mathbb {E} \left(\mathrm {e} ^{tX}\right)=\int _{-\infty }^{+\infty }\mathrm {e} ^{tx}f_{X}(x)\,\mathrm {d} x$ .

Son nom est justifié par le fait qu'en utilisant le développement en série entière de la fonction exponentielle, on a :

M_{X}(t)=\mathbb {E} \left(\mathrm {e} ^{tX}\right)=\mathbb {E} \left(\sum _{n=0}^{+\infty }{\frac {t^{n}X^{n}}{n!}}\right)=\sum _{n=0}^{+\infty }{\frac {t^{n}}{n!}}\mathbb {E} (X^{n})

.

Ainsi, on trouve :

Propriété

$\mathbb {E} (X^{n})=M_{X}^{(n)}(0)$ .

Fonction caractéristique

Cette fonction, semblable à la fonction génératrice mais à valeurs dans $\mathbb {C}$ , est une autre fonction qui caractérise la loi d'une variable aléatoire.

Fonction caractéristique

Si X est une variable aléatoire qui admet pour fonction de densité $f_{X}$ , sa fonction caractéristique est définie par :

$\varphi _{X}(t)=\mathbb {E} \left(\mathrm {e} ^{\mathrm {i} tX}\right)=\int _{-\infty }^{+\infty }\mathrm {e} ^{\mathrm {i} tx}f_{X}(x)\,\mathrm {d} x$ .

De même façon que pour la fonction génératrice, on trouve :

Propriété

$\mathbb {E} (X^{n})=\mathrm {i} ^{n}\varphi _{X}^{(n)}(0)$ .

Il existe cependant un autre théorème, très important :

Théorème

Soient X et Y deux variables aléatoires réelles. Alors X et Y ont même loi si et seulement si $\forall t\in \mathbb {R} \quad \mathbb {E} \left(\mathrm {e} ^{\mathrm {i} tX}\right)=\mathbb {E} \left(\mathrm {e} ^{\mathrm {i} tY}\right)$ .

Ce théorème sera admis.

Médiane, mode

Quand les moments ne peuvent être calculés, on peut néanmoins donner une idée de l'allure de la densité en déterminant la (ou les) médiane(s) et le(s) mode(s).

La médiane se définit comme une valeur qui permet de séparer en deux parties les échantillons ou la distribution d'une variable aléatoire de sorte que chacune des deux parties contiennent le même nombre de valeurs.

Médiane

On appelle médiane d'une variable aléatoire, tout nombre m qui satisfait l'égalité :

$\mathbb {P} (X\leq m)=\mathbb {P} (X\geq m)$

Le mode, quant à lui, représente la valeur la plus représentée dans la densité.

Mode

On appelle mode d'une variable aléatoire, toute valeur $c_{0}$ qui satisfait :

$f_{X}(X=c_{0})=\max _{c\in \mathbb {R} }f_{X}(X=c)$

Il n'y a aucune garantie de l'unicité des médianes ou des modes dans le cas général.

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.