Suites et séries de fonctions/Suites de fonctions

On considère dans cette leçon des fonctions d'une variable réelle.

Définition : Suite de fonctions

Une suite de fonctions est une suite $(f_{n})$ à valeurs dans $\mathbb {R} ^{\mathbb {R} }$ (l'ensemble des fonctions d'une variable réelle), c'est-à-dire qu'elle associe à chaque entier naturel $n$ la fonction $f_{n}$ :

(f_{n}):{\begin{array}{lcl}\mathbb {N} &\rightarrow &\mathbb {R} ^{\mathbb {R} }\\n&\mapsto &f_{n}\end{array}}

Exemple

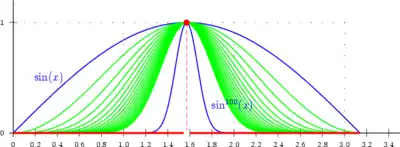
Voici la représentation graphique pour quelques valeurs de $n$ de la suite de fonctions $(f_{n})$ définie par $f_{n}(x)=\sin ^{n}x\;\forall n\in \mathbb {N}$ sur l'intervalle $[0;\pi ]$ .

Convergence simple

Définition : Convergence simple d'une suite de fonctions

Soit $(f_{n})$ une suite de fonctions définies sur ${\mathcal {D}}\subset \mathbb {R}$ .

On dit que $(f_{n})$ converge simplement vers la fonction $f$ si pour chaque réel $x$ de ${\mathcal {D}}$ , la suite numérique $(f_{n}(x))$ converge vers le réel $f(x)$ .

Dans le « langage des $\varepsilon$ », cela donne :

$\forall x\in {\mathcal {D}}\quad \forall \varepsilon >0\quad \exists n_{\varepsilon ,x}\in \mathbb {N} \quad \forall n\in \mathbb {N} \quad n\geq n_{\varepsilon ,x}\Rightarrow |f_{n}(x)-f(x)|<\varepsilon$ .

Cela signifie qu'on se fixe une valeur de $x\in {\mathcal {D}}$ et qu'on étudie la convergence d'une suite « paramétrée par $x$ » qui est la suite $(f_{n}(x))$ .

Exemple

La figure ci-dessus permet de penser que la suite de fonctions $(f_{n})$ converge simplement vers la fonction $f$ définie sur $[0,\pi ]$ par :

f:x\mapsto {\begin{cases}0,\mathrm {\;si\;} x\neq {\frac {\pi }{2}}\\1,\mathrm {\;si\;} x={\frac {\pi }{2}}\end{cases}}

Pour le démontrer, il suffit de remarquer que $\forall x\in [0,\pi ]\setminus \left\{{\frac {\pi }{2}}\right\}\quad |\sin x|<1$ . On a donc dans ce cas affaire à une suite $(f_{n}(x))$ géométrique de raison $\sin x$ qui converge donc vers $0$ . La suite $(f_{n}({\frac {\pi }{2}}))$ est constante et converge vers $1$ .

On remarque dans cet exemple que la convergence simple ne permet pas de maîtriser les propriétés analytiques de la fonction limite : la suite de fonctions ici considérée est une suite de fonctions continues mais la fonction limite présente une discontinuité en ${\frac {\pi }{2}}$ . C'est ce qui motive l’introduction de la notion de convergence uniforme.

Convergence uniforme

Intuitivement, la convergence uniforme est une convergence qui a lieu "uniformément" (c'est-à-dire "à la même vitesse") sur tout le domaine de définition ${\mathcal {D}}$ . Ce n’est pas le cas pour l'exemple choisi ici : en effet, il existe une "bosse" en ${\frac {\pi }{2}}$ qui "persiste" lors du passage à la limite.

Définition : Convergence uniforme d'une suite de fonctions

Soit $(f_{n})$ une suite de fonctions définies sur ${\mathcal {D}}\subset \mathbb {R}$ .

On dit que $(f_{n})$ converge uniformément vers la fonction $f$ si :
$\forall \varepsilon >0\quad \exists n_{\varepsilon }\in \mathbb {N} \quad \forall n\in \mathbb {N} \quad n\geq n_{\varepsilon }\Rightarrow \forall x\in {\mathcal {D}}\quad |f_{n}(x)-f(x)|\leq \varepsilon$ .
Cela équivaut à dire que la suite de terme général $\|f_{n}-f\|_{\infty }=\sup _{x\in {\mathcal {D}}}|f_{n}(x)-f(x)|$ converge vers $0$ , c'est-à-dire :
$\forall \varepsilon >0\quad \exists n_{\varepsilon }\in \mathbb {N} \quad \forall n\in \mathbb {N} \quad n\geq n_{\varepsilon }\Rightarrow \|f_{n}-f\|_{\infty }<\varepsilon$ .

On abrègera « convergence simple » en « CVS » et « convergence uniforme » en « CVU ».

Remarque Sur l'espace ${\mathcal {C}}^{0}({\mathcal {D}})$ , (où ${\mathcal {D}}$ est un compact), la norme « infinie » ou norme sup ou encore norme de la convergence uniforme s'écrit :

{\|f\|}_{\infty }=\sup _{t\in {\mathcal {D}}}|f(t)|

.

Exemple

Soit la suite de fonctions $f_{n}:x\mapsto \mathrm {e} ^{-nx}$ définies sur $\left[1,+\infty \right[$ .

Montrer que cette suite converge uniformément vers la fonction nulle.

Solution

Pour tout réel $x\geq 1$ , on a $0<f_{n}(x)\leq f_{n}(1)=\mathrm {e} ^{-n}$ . Donc

\|f_{n}-f\|_{\infty }=\mathrm {e} ^{-n}{\xrightarrow[{n\to +\infty }]{}}0

.

On en déduit le résultat voulu :

(f_{n}){\xrightarrow[{n\to +\infty }]{CVU}}0

.

Propriétés des suites de fonctions

Propriétés de la convergence simple

La convergence simple possède des propriétés assez faibles. On peut toutefois énoncer les propriétés suivantes :

Propriétés

Soit $(f_{n}){\xrightarrow[{n\to +\infty }]{CVS}}f$ sur ${\mathcal {D}}\subset \mathbb {R}$ .
Si $\forall n\in \mathbb {N}$ la fonction $f_{n}$ est croissante sur ${\mathcal {D}}$ , alors la fonction limite $f$ est croissante sur ${\mathcal {D}}$ .
La propriété reste vraie en remplaçant "croissante" par "décroissante", "paire", "impaire" (pour la parité, le domaine ${\mathcal {D}}$ doit être symétrique par rapport à $0$ ).

(démonstration et exemple à faire)

Propriétés de la convergence uniforme

Elles sont beaucoup plus nombreuses et fortes. Tout d’abord :

Théorème

Toute suite de fonctions uniformément convergente est simplement convergente.

La réciproque est fausse (voyez le premier exemple ci-dessus).

Démonstration

Si $\forall \varepsilon >0,\exists n_{\varepsilon }\in \mathbb {N} |\forall x\in {\mathcal {D}},\forall n\in \mathbb {N} ,n\geq n_{\varepsilon ,}\Rightarrow |f_{n}(x)-f(x)|<\varepsilon$ , alors $\forall x\in {\mathcal {D}},\forall \varepsilon >0,\exists n_{\varepsilon ,x}=n_{\varepsilon }\in \mathbb {N} |\forall n\in \mathbb {N} ,n\geq n_{\varepsilon ,x}\Rightarrow |f_{n}(x)-f(x)|<\varepsilon$ .
"En clair", si pour tout $\varepsilon >0$ , je peux trouver un rang $n_{\varepsilon }$ tel que la convergence ait lieu indépendamment de $x$ alors, pour tout $x$ , je peux trouver un rang $n_{\varepsilon ,x}=n_{\varepsilon }$ tel que la convergence ait lieu.

Théorème d'interversion des limites

Soit $(f_{n}){\xrightarrow[{n\to +\infty }]{CVU}}f$ sur ${\mathcal {D}}\subset \mathbb {R}$ et soit $a$ un point adhérent à ${\mathcal {D}}$ .

Si pour tout $n$ , $\ell _{n}=\lim _{a}f_{n}$ existe, alors les deux limites $\lim _{a}f$ et $\lim _{n\to +\infty }\ell _{n}$ existent et sont égales, autrement dit :

$\lim _{x\to a}\left(\lim _{n\to +\infty }f_{n}(x)\right)=\lim _{n\to +\infty }\left(\lim _{x\to a}f_{n}(x)\right)$ .

La démonstration repose de façon cruciale sur la convergence des suites de Cauchy dans $\mathbb {R}$ . Pour un énoncé plus général — dans lequel le critère de Cauchy pour les suites est étendu aux fonctions — voir « Corollaire : théorème d'interversion des limites » dans la leçon de topologie (de niveau 16).

Démonstration

Par hypothèse, pour tout $\varepsilon >0$ :

puisque $(f_{n}){\xrightarrow[{n\to +\infty }]{CVU}}f$ : $\exists n_{\varepsilon }\in \mathbb {N} \quad \forall x\in {\mathcal {D}}\quad \forall n\in \mathbb {N} \quad n\geq n_{\varepsilon }\Rightarrow |f_{n}(x)-f(x)|<\varepsilon \qquad (*)$ ;
puisque $\lim _{a}f_{n}=\ell _{n}$ : $\forall n\in \mathbb {N} \quad \exists \eta _{\varepsilon ,n}>0\quad \forall x\in {\mathcal {D}}\quad |x-a|<\eta _{\varepsilon ,n}\Rightarrow |f_{n}(x)-\ell _{n}|<\varepsilon$ .

Pour $p,q\geq n_{\varepsilon }$ fixés, on déduit de $(*)$ que $\forall x\in {\mathcal {D}}\quad |f_{p}(x)-f_{q}(x)|<2\varepsilon$ donc (par passage à la limite quand $x\to a$ ) $|\ell _{p}-\ell _{q}|\leq 2\varepsilon$ .

Ceci prouve que la suite $(\ell _{n})$ est de Cauchy. Elle admet donc une limite $\ell$ , qui vérifie (par passage à la limite quand $q\to +\infty$ ) : $\forall p\geq n_{\varepsilon }\quad |\ell _{p}-\ell |\leq 2\varepsilon$ .

Soit $\delta _{\varepsilon }=\eta _{\varepsilon ,n_{\varepsilon }}$ . Pour tout $x\in {\mathcal {D}}\cap \left]a-\delta _{\varepsilon },a+\delta _{\varepsilon }\right[$ , on a :

|f(x)-\ell |\leq |f(x)-f_{n_{\varepsilon }}(x)|+|f_{n_{\varepsilon }}(x)-\ell _{n_{\varepsilon }}|+|\ell _{n_{\varepsilon }}-\ell |<4\varepsilon

,

ce qui prouve que $\lim _{a}f=\ell$ .

Corollaire

La limite d'une suite uniformément convergente de fonctions continues est continue.

La contraposée de ce corollaire est pariculièrement utile : si une suite de fonctions continues converge vers une fonction discontinue, alors cette convergence n'est pas uniforme.

Exemple

On considère une fonction $f:[0,1]\to [0,1]$ strictement croissante telle que $f(1)=1$ . Étudier la convergence (simple et uniforme) de la suite $(f^{n})$ .

Solution

$(f^{n})$ converge simplement vers la fonction $f$ indicatrice de $\{1\}$ , qui est discontinue. La convergence n’est donc pas uniforme. Remarquons qu'on a tout de même $\int _{0}^{1}f^{n}\to 0=\int _{0}^{1}f$ . En effet, pour tout $\varepsilon >0$ , $\int _{0}^{1-\varepsilon }f^{n}\to 0$ (par convergence uniforme sur $[0,1-\varepsilon ]$ ou simplement par majoration par $(1-\varepsilon )f^{n}(1-\varepsilon )$ ) et $\int _{1-\varepsilon }^{1}f^{n}\leq \varepsilon$ .

Théorème d'interversion limite-dérivée

Soit $f_{n},g$ définies sur un intervalle ouvert ${\mathcal {D}}\subset \mathbb {R}$ .

Si :

$(f'_{n}){\xrightarrow[{n\to +\infty }]{CVU}}g$ sur ${\mathcal {D}}$ ;
il existe un point $a\in {\mathcal {D}}$ tel que $\left(f_{n}\left(a\right)\right)$ converge ;

alors :

la suite $\left(f_{n}\right)$ converge simplement vers une fonction $f$ définie sur ${\mathcal {D}}$ (la convergence est même uniforme sur tout sous-intervalle borné de ${\mathcal {D}}$ ) ;
cette fonction $f$ est dérivable et $f'=g$ , autrement dit :

${\frac {\mathrm {d} }{\mathrm {d} x}}\left(\lim _{n\to +\infty }f_{n}\right)=\lim _{n\to +\infty }\left({\frac {\mathrm {d} }{\mathrm {d} x}}f_{n}\right)$

.

(Si les $f'_{n}$ sont continues, $f'$ le sera donc également.)

Démonstration

Calcul différentiel/Théorèmes utiles#Théorème de différentiation terme à terme

Exemple

Pour $n\in \mathbb {N}$ et $x\in [0,\pi /2]$ , on note $f_{n}(x)=n\cos ^{n}x\sin x$ .

Montrer que la suite de fonctions $(f_{n})$ converge simplement mais pas uniformément.

Solution

$f_{n}(0)=0$ et pour tout $x\in \left]0,\pi /2\right]$ , $f_{n}(x)\to 0$ (par croissances comparées). Cependant, $\int _{0}^{\pi /2}f_{n}=\int _{1}^{0}nt^{n}\,(-\mathrm {d} t)={\frac {n}{n+1}}\to 1$ . La convergence de $(f_{n})$ vers $0$ n'est donc pas uniforme sur $[0,\pi /2]$ (elle l'est seulement sur $[\varepsilon ,\pi /2]$ pour tout $\varepsilon >0$ ). C'est même pire et l'on peut d'ailleurs le redémontrer directement : $\forall x\in [0,\pi /2]\quad 0\leq f_{n}(x)\leq f_{n}\left(\arctan {\frac {1}{\sqrt {n}}}\right)$ donc $\|f_{n}\|_{\infty }={\sqrt {n}}\left(1+{\frac {1}{n}}\right)^{-{\frac {n+1}{2}}}\sim {\sqrt {\frac {n}{\mathrm {e} }}}\to +\infty$ .

Théorème d'interversion limite-intégrale

Soit $(f_{n}){\xrightarrow[{n\to +\infty }]{CVU}}f$ sur ${\mathcal {D}}\subset \mathbb {R}$ et soient $a<b\in {\mathcal {D}}$ . On suppose de plus que $f_{n}$ est continue par morceaux sur $[a,b]\subset {\mathcal {D}}$ pour tout $n\in \mathbb {N}$ .

Alors :

$\int _{a}^{b}\lim _{n\to +\infty }f_{n}(x)\;\mathrm {d} x=\lim _{n\to +\infty }\int _{a}^{b}f_{n}(x)\;\mathrm {d} x$ .

C'est un corollaire du théorème précédent, grâce au théorème fondamental de l'analyse.

Avertissement :

Sur un intervalle non borné, la convergence uniforme d'une suite de fonctions n'implique pas la convergence de la suite de leurs intégrales.

Exemple : soit $f:\mathbb {R} \to \mathbb {R}$ une fonction bornée, intégrable et d'intégrale non nulle. Posons $f_{n}(x)={\frac {1}{n}}f\left({\frac {x}{n}}\right)$ .

Alors, $\|f_{n}\|_{\infty }={\frac {1}{n}}\|f\|_{\infty }\to 0$ mais $\int _{-\infty }^{+\infty }f_{n}=\int _{-\infty }^{+\infty }f\neq 0$ .

Enfin, on a le

Théorème de convergence dominée (Lebesgue)

Si :

$f_{n}$ est continue par morceaux sur $[a,b]$ pour tout $n\in \mathbb {N}$ ;
la suite de fonctions $(f_{n})$ converge simplement vers une fonction $f$ continue par morceaux sur $[a,b]$ ;
il existe une fonction $g$ continue par morceaux sur $[a,b]$ telle que :

\forall n\in \mathbb {N} \quad \forall x\in [a,b]\quad |f_{n}(x)|\leq g(x)

(hypothèse de domination) ;

alors

$\int _{a}^{b}\lim _{n\to +\infty }f_{n}(x)\;\mathrm {d} x=\lim _{n\to +\infty }\int _{a}^{b}f_{n}(x)\;\mathrm {d} x$ .

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.