Calcul différentiel/Exercices/Courbes paramétrées

Exercice 1

Soit un réel $a>0$ .

Étudier et tracer la courbe paramétrée $x=a\cos ^{3}t,y=a\sin ^{3}t$ .
Pour $t\in \left]0,{\frac {\pi }{2}}\right[$ , on note $A(t)$ et $B(t)$ les points d'intersection de la tangente à cette courbe au point $M(t)$ avec, respectivement, $(Ox)$ et $(Oy)$ . Calculer la distance $A(t)B(t)$ .

Solution

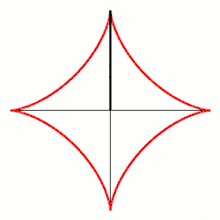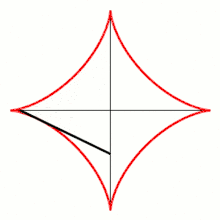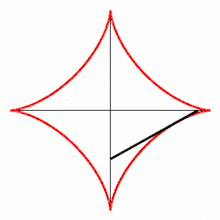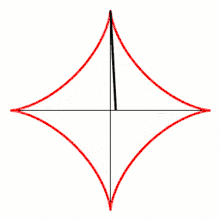
http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 1, question 1.

- On peut se limiter à $t\in \left[-\pi ,\pi \right]$ par périodicité, puis se restreindre à $\left[0,\pi \right]$ car $M(-t)$ est le symétrique de $M(t)$ par rapport à $(Ox)$ , puis à $\left[0,\pi /2\right]$ car $M(\pi -t)$ est le symétrique de $M(t)$ par rapport à $(Oy)$ , puis à $\left[0,\pi /4\right]$ car $M(\pi /2-t)$ est le symétrique de $M(t)$ par rapport à la droite $y=x$ .
- $\left(x'(t),y'(t)\right)=3a\cos t\sin t\left(-\cos t,\sin t\right)$ s'annule en $t=0$ et vaut ${\frac {3a}{2{\sqrt {2}}}}\left(-1,1\right)$ en $t={\frac {\pi }{4}}$ .
- $M(0)=\left(a,0\right)$ et $M\left(\pi /4\right)={\frac {a}{2{\sqrt {2}}}}\left(1,1\right)$ . Quand $t$ croît de $0$ à $\pi /4$ , $x(t)$ décroît et $y(t)$ croît.
- Au voisinage de $t=0$ , $M(t)=a\left(1-3t^{2}/2,t^{3}\right)+o\left(t^{3}\right)$ donc il s'agit d'un point de rebroussement de première espèce à tangente horizontale.
$\left(x'(t),y'(t)\right)\perp \left(\sin t,\cos t\right)$ donc la tangente au point $M(t)$ a pour équation : $\left(x-a\cos ^{3}t\right)\sin t+\left(y-a\sin ^{3}t\right)\cos t=0$ , soit $x\sin t+y\cos t=a\cos t\sin t$ . Par conséquent, $A(t)=\left(a\cos t,0\right)$ et $B(t)=\left(0,a\sin t\right)$ donc $A(t)B(t)=a$ .

Exercice 2

Soit un réel $R>0$ .

Un cercle ${\mathcal {C}}$ , de rayon $R$ , roule sans glisser sur l'axe $(Ox)$ . On note $I$ le point de contact entre ${\mathcal {C}}$ et $(Ox)$ et $\Omega$ le centre du cercle ${\mathcal {C}}$ ( $I$ et $\Omega$ sont donc mobiles). $M$ est un point donné de ${\mathcal {C}}$ (mobile, mais solidaire de ${\mathcal {C}}$ ). Déterminer un paramétrage par $t:={\widehat {M\Omega I}}$ de la courbe décrite par le point $M$ .
Étudier et tracer la courbe paramétrée $x=R\left(t-\sin t\right),y=R\left(1-\cos t\right)$ .

Solution

http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 1, question 2.

Quand $t$ augmente de $\mathrm {d} t$ , l'abscisse $a(t)$ de $I$ et $\Omega$ augmente de $R\mathrm {d} t$ . Donc $M(t)=\left(a(t)-R\sin t,R\left(1-\cos t\right)\right)$ avec $a'(t)=R$ , c.-à-d.
$\left(x(t),y(t)\right)=\left(a(0)+R\left(t-\sin t\right),R\left(1-\cos t\right)\right)$ .
- On peut se limiter à étudier la courbe pour $t\in \left[-\pi ,\pi \right]$ car $M(t+2\pi )$ est le translaté de $M(t)$ par $\left(2\pi R,0\right)$ , puis se restreindre à $\left[0,\pi \right]$ car $M(-t)$ est le symétrique de $M(t)$ par rapport à $(Oy)$ .
- $\left(x'(t),y'(t)\right)=R\left(1-\cos t,\sin t\right)$ s'annule en $t=0$ et vaut $R\left(2,0\right)$ (donc tangente horizontale) en $t=\pi$ .
- $M(0)=\left(0,0\right)$ et $M(\pi )=R\left(\pi ,2\right)$ . Quand $t$ croît de $0$ à $\pi$ , $x(t)$ et $y(t)$ croissent.
- Au voisinage de $t=0$ , $M(t)=R\left(t^{3}/6,t^{2}/2\right)+o\left(t^{3}\right)$ donc il s'agit d'un point de rebroussement de première espèce à tangente verticale.

Exercice 3

1. On considère

x(\theta )=\sin(p\theta ),\,y(\theta )=\sin(q\theta ),\quad \theta \in [0,2\pi ]

.

Dans les deux cas suivants, établir le double tableau de variations et tracer la courbe associée :

{\text{a) }}p=1,\,q=2\,;\quad {\text{b) }}p=2,\,q=3

.

2. Étudier et tracer la courbe paramétrée

x={\frac {t}{1+t^{4}}},\,y={\frac {t^{3}}{1+t^{4}}}

.

En donner une équation cartésienne.

Solution

1. a) $M(t+\pi )$ est l'image de $M(t)$ par la symétrie orthogonale par rapport à l'axe $Oy$ . On peut donc restreindre $t$ à $\left[0,\pi \right]$ . Puis, $M(\pi -t)$ est l'image de $M(t)$ par la symétrie orthogonale par rapport à l'axe $Ox$ . On peut donc même restreindre $t$ à $\left[0,\pi /2\right]$ .
Sur cet intervalle, $x'=\cos >0,\,y'(t)=2\cos(2t)$ , d'où le tableau de variations suivant :

{\begin{array}{|c|lcccc|}\hline t&0&&\pi /4&&\pi /2\\\hline &&&&&1\\&&&&\nearrow &\\x&&&1/{\sqrt {2}}&&&\\&&\nearrow &&\\&0&&&&\\\hline &&&1&&\\y&&\nearrow &&\searrow &\\&0&&&&0\\\hline \end{array}}

La tangente en $M(0)$ a pour pente $y'(0)/x'(0)=2$ , et la tangente en $M(\pi /2)$ est verticale (car $x'(\pi /2)=0\neq y'(\pi /2)$ ).

Courbe sous google.com (c'est à peu de chose près la lemniscate de Gerono).

1. b) http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 1, question 3.

2. http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 1, question 4.

$y=t^{2}x$ donc $x^{2}={\frac {y/x}{(1+(y/x)^{2})^{2}}}$ , soit encore : $xy=(x^{2}+y^{2})^{2}$ .

Exercice 4

Construire les courbes paramétrées :

$x={\frac {t^{3}}{\left(t+1\right)^{2}\left(t-1\right)}},\,y={\frac {t^{2}}{t^{2}-1}}$ ;
$x=\left(t+2\right)\operatorname {e} ^{1/t},\,y=\left(t-2\right)\operatorname {e} ^{1/t}$ ;
$x=\left(t-1\right)\ln |t|,\,y=\left(t+1\right)\ln |t|$ ;
$x={\frac {2t}{1+t^{2}}},\,y={\frac {t+2}{1-t^{2}}}$ ;
$x={\frac {t}{t^{2}-1}},\,y={\frac {t+2}{\left(t-1\right)^{2}}}$ ;
$x={\frac {t^{3}}{t^{2}-9}},\,y={\frac {t\left(t-2\right)}{t-3}}$ ;
$x={\frac {t^{3}}{1+3t}},\,y={\frac {3t^{2}}{1+3t}}$ ;
$x=t^{2}+t^{3},\,y=t^{2}+t^{3}-2t^{4}-2t^{5}$ ;
$x=t-{\frac {1}{t}},\,y=t-{\frac {\ln {(2\operatorname {e} ^{t}-1)}}{2}}$ ;
$x=t^{2}+{\frac {2}{t}},\,y=t^{2}+{\frac {1}{t^{2}}}$ .

Solution

Pour les questions 1 à 8, voir aussi http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 2.

On étudie $x={\frac {t^{3}}{\left(t+1\right)^{2}\left(t-1\right)}},\,y={\frac {t^{2}}{t^{2}-1}}$ pour $t\neq \pm 1$ . Calculons les dérivées logarithmiques pour $t\in \mathbb {R} \setminus \{-1,0,1\}$ :
${\frac {x'}{x}}={\frac {3}{t}}-{\frac {2}{t+1}}-{\frac {1}{t-1}}={\frac {3\left(t^{2}-1\right)-2\left(t^{2}-t\right)-\left(t^{2}+t\right)}{t\left(t+1\right)\left(t-1\right)}}={\frac {t-3}{t\left(t+1\right)\left(t-1\right)}}$ et
${\frac {y'}{y}}={\frac {2}{t}}-{\frac {1}{t+1}}-{\frac {1}{t-1}}={\frac {2\left(t^{2}-1\right)-\left(t^{2}-t\right)-\left(t^{2}+t\right)}{t\left(t+1\right)\left(t-1\right)}}={\frac {-2}{t\left(t+1\right)\left(t-1\right)}}$ donc
$x'={\frac {t^{2}\left(t-3\right)}{\left(t+1\right)^{3}\left(t-1\right)^{2}}}$ et $y'={\frac {-2t}{\left(t+1\right)^{2}\left(t-1\right)^{2}}}$ .
Par continuité, ces égalités sont encore vraies pour $t=0$ .
On en déduit le tableau de variations suivant :
${\begin{array}{|c|lccccc|}\hline t&-\infty &-1&0&1&3&+\infty \\\hline x&{\begin{matrix}&&+\infty \\&\nearrow &\\1&&\\&&\end{matrix}}&{\Big \Vert }&{\begin{matrix}+\infty &&&&\\&\searrow &&&\\&&0&&\\&&&&\searrow &\\&&&&&-\infty \end{matrix}}&{\Big \Vert }&{\begin{matrix}+\infty &&&&\\&\searrow &&&1\\&&&\nearrow &&\\&&{\frac {27}{32}}&&\end{matrix}}\\\hline y&{\begin{matrix}&&+\infty \\&\nearrow &\\1&&\\&&\end{matrix}}&{\Big \Vert }&{\begin{matrix}&&&&\\&&0&&\\&\nearrow &&\searrow &\\-\infty &&&&+\infty \end{matrix}}&{\Big \Vert }&{\begin{matrix}+\infty &&&&\\&\searrow &&&\\&&{\frac {9}{8}}&&\\&&&&\searrow &\\&&&&&1\end{matrix}}\\\hline \end{array}}$
Quand $t\to \pm \infty$ , ${\frac {y-1}{x-1}}\sim {\frac {1/t^{2}}{-1/t}}=-{\frac {1}{t}}\to 0$ donc au point limite $\left(1,1\right)$ , la tangente est horizontale.
Quand $t\to -1$ , ${\frac {y}{x}}\sim {\frac {\frac {1}{-2\left(t+1\right)}}{\frac {1}{2\left(t+1\right)^{2}}}}=-\left(t+1\right)\to 0$ donc la courbe a deux branches paraboliques de direction horizontale.
Quand $t\to +1$ , ${\frac {y}{x}}\sim {\frac {\frac {1}{2\left(t-1\right)}}{\frac {1}{4\left(t-1\right)}}}=2$ et $y-2x={\frac {t^{2}\left(t+1\right)-2t^{3}}{\left(t+1\right)^{2}\left(t-1\right)}}={\frac {-t^{2}}{\left(t+1\right)^{2}}}\to -{\frac {1}{4}}$ donc la courbe a une asymptote d'équation $y=2x-{\frac {1}{4}}$ .
Quand $t\to 0$ , $x\sim -t^{3}$ et $y\sim -t^{2}$ donc le point singulier $\left(0,0\right)$ est un point de rebroussement de première espèce à tangente verticale.
Il y a nécessairement un point d'inflexion sur la branche parabolique qui part du point limite. Calculons-le. La courbure ${\frac {x'y''-y'x''}{\left(x'^{2}+y'^{2}\right)^{3/2}}}$ s'annule lorsque les dérivées logarithmiques de $x'$ et $y'$ sont égales, c'est-à-dire ${\frac {2}{t}}+{\frac {1}{t-3}}-{\frac {3}{t+1}}-{\frac {2}{t-1}}={\frac {1}{t}}-{\frac {2}{t+1}}-{\frac {3}{t-1}}$ soit, après simplification : $0=t^{2}+2t-3=\left(t-1\right)\left(t+3\right)$ donc $t=-3,x={\frac {27}{16}},y={\frac {9}{8}},{\frac {y'}{x'}}={\frac {2}{9}}$ .
$x'={\frac {(t+1)(t-2)}{t^{2}}}\operatorname {e} ^{1/t},\,y'={\frac {t^{2}-t+2}{t^{2}}}\operatorname {e} ^{1/t}>0$ . En calculant les limites aux bornes, on aboutit au tableau suivant :
${\begin{array}{|c|lcccccc|}\hline t&-\infty &&-1&&&0&&&2&&+\infty \\\hline &&&{\frac {1}{2}}&&&{\Big \Vert }&+\infty &&&&+\infty \\x&&\nearrow &&\searrow &&{\Big \Vert }&&\searrow &&\nearrow &\\&-\infty &&&&0&{\Big \Vert }&&&4{\sqrt {\mathrm {e} }}&&\\\hline &&&&&0&{\Big \Vert }&&&&&+\infty \\&&&&\nearrow &&{\Big \Vert }&&&&\nearrow &\\y&&&-3/2&&&{\Big \Vert }&&&0&&\\&&\nearrow &&&&{\Big \Vert }&&\nearrow &&&\\&-\infty &&&&&{\Big \Vert }&-\infty &&&&\\\hline \end{array}}$
Quand $t\to \pm \infty$ , $y-x\to -4$ donc asymptote d'équation $y=x-4$ .
Quand $t\to 0^{+}$ , $y/x\to -1$ et $y+x\to +\infty$ donc branche parabolique de direction $y=-x$ .
Au point limite $M(0^{-})=(0,0)$ , la tangente a pour pente $\lim _{t\to 0}{\frac {y}{x}}=-1$ .
$M(-t)$ est l'image de $M(t)$ par la symétrie orthogonale par rapport à la droite $y=-x$ . On peut donc restreindre $t$ à $\left]0,+\infty \right[$ .
Sur cet intervalle, $x'=\ln t+1-{\frac {1}{t}},\,y'=\ln t+1+{\frac {1}{t}}$ ; $x''={\frac {1}{t}}+{\frac {1}{t^{2}}}>0,\,y''={\frac {t-1}{t^{2}}}$ ; $x'(1)=0,\,y'(1)=2>0$ , d'où le tableau de variations suivant :
${\begin{array}{|c|lccccc|}\hline t&0&&1&&+\infty \\\hline &+\infty &&&&+\infty \\x&&\searrow &&\nearrow &\\&&&0&&\\\hline &&&&&+\infty \\&&&&\nearrow &\\y&&&0&&\\&&\nearrow &&&\\&-\infty &&&&\\\hline \end{array}}$
Quand $t\to 0^{+}$ , $y/x\to -1$ et $y+x\to -\infty$ , d'où une branche parabolique de direction $y=-x$ .
Quand $t\to +\infty$ , $y/x\to 1$ et $y-x\to -\infty$ , d'où une branche parabolique de direction $y=x$ .
$M(1/t)$ est l'image de $M(t)$ par la symétrie orthogonale par rapport à la droite $y=1$ . On peut donc restreindre $t$ à $\left]-1,1\right[$ .
Sur cet intervalle, $x'=2{\frac {1-t^{2}}{1+t^{2}}}>0,\,y={\frac {(t+2)^{2}-3}{1-t^{2}}}$ , d'où le tableau de variations suivant :
${\begin{array}{|c|lcccc|}\hline t&-1&&{\sqrt {3}}-2&&1\\\hline &&&&&1\\&&&&\nearrow &\\x&&&-1/2&&&\\&&\nearrow &&\\&-1&&&&\\\hline &+\infty &&&&+\infty \\y&&\searrow &&\nearrow &\\&&&1+{\frac {\sqrt {3}}{2}}&&\\\hline \end{array}}$
On étudie $x={\frac {t}{t^{2}-1}},y={\frac {t+2}{\left(t-1\right)^{2}}}$ pour $t\in \mathbb {R} \setminus \{-1,1\}$ .
$x'=-{\frac {t^{2}+1}{\left(t^{2}-1\right)^{2}}}<0,\quad y'={\frac {-t^{2}-4t+5}{\left(t-1\right)^{4}}}=-{\frac {t+5}{\left(t-1\right)^{3}}}$ .
Il n'y a donc pas de point singulier, et au point $\left(x,y\right)\left(-5\right)=\left(-{\frac {5}{24}},-{\frac {3}{16}}\right)$ , la tangente est horizontale.
La courbe coupe l'axe des abscisses en $\left(x,y\right)\left(-2\right)=\left(-{\frac {2}{3}},0\right)$ , avec une tangente de pente ${\frac {y'\left(-2\right)}{x'\left(-2\right)}}=-{\frac {1}{5}}$ , et l'axe des ordonnées en $\left(x,y\right)\left(0\right)=\left(0,2\right)$ , avec une tangente de pente ${\frac {y'\left(0\right)}{x'\left(0\right)}}=-5$ .
$\left(x,y\right)\sim _{t\to \pm \infty }\left({\frac {1}{t}},{\frac {1}{t}}\right)$ donne un point limite $\left(0,0\right)$ à tangente de pente $1$ .
$\left(x,y\right)\sim _{t\to -1}\left({\frac {1}{2\left(t+1\right)}},{\frac {1}{4}}\right)$ donne une asymptote horizontale.
La position de la courbe par rapport à cette asymptote est donnée par le signe de $y\left(t\right)-{\frac {1}{4}}=-{\frac {(t+1)(t-7)}{4\left(t-1\right)^{2}}}$ , donc la courbe est au-dessus si $-1<t<7$ et en dessous sinon.
$\left(x,y\right)\sim _{t\to 1}\left({\frac {1}{2\left(t-1\right)}},{\frac {3}{\left(t-1\right)^{2}}}\right)$ donne deux branches paraboliques de direction verticale car ${\frac {y}{x}}\sim _{t\to 1}{\frac {6}{t-1}}\to \pm \infty$ .
La courbe s'auto-intersecte au point $\left({\frac {1}{3}},1\right)$ ( $t_{1}t_{2}=-1,t_{1}+t_{2}=3,t_{i}^{2}=3t_{i}+1$ ).
$x'={\frac {t^{2}\left(t^{2}-27\right)}{\left(t^{2}-9\right)^{2}}},\,y'=1-{\frac {3}{(t-3)^{2}}}$ , d'où le tableau suivant :
${\begin{array}{|c|lcccccccccccccccccc|}\hline t&-\infty &&-3{\sqrt {3}}&&&-3&&&3-{\sqrt {3}}&&&3&&&3+{\sqrt {3}}&&3{\sqrt {3}}&&+\infty \\\hline &&&&&&{\Big \Vert }&+\infty &&&&&{\Big \Vert }&+\infty &&&&&&+\infty \\&&&&&&{\Big \Vert }&&\searrow &&&&{\Big \Vert }&&\searrow &&&&\\x&&&{\frac {-9{\sqrt {3}}}{2}}&&&{\Big \Vert }&&&{\frac {2(21+13{\sqrt {3}})}{11}}&&&{\Big \Vert }&&&{\frac {2(21-13{\sqrt {3}})}{11}}&&&\nearrow &\\&&\nearrow &&\searrow &&{\Big \Vert }&&&&\searrow &&{\Big \Vert }&&&&\searrow &&&\\&-\infty &&&&-\infty &{\Big \Vert }&&&&&-\infty &{\Big \Vert }&&&&&{\frac {9{\sqrt {3}}}{2}}&&\\\hline &&&&&&&&&2-2{\sqrt {3}}&&&{\Big \Vert }&+\infty &&&&&&+\infty \\&&&&&&&&\nearrow &&&&{\Big \Vert }&&&&&&\nearrow &\\&&&&&&{\frac {-5}{2}}&&&&&&{\Big \Vert }&&\searrow &&&{\frac {3+7{\sqrt {3}}}{2}}&&\\y&&&&\nearrow &&&&&&\searrow &&{\Big \Vert }&&&&\nearrow &&&\\&&&{\frac {3-7{\sqrt {3}}}{2}}&&&&&&&&&{\Big \Vert }&&&2+2{\sqrt {3}}&&&&\\&&\nearrow &&&&&&&&&&{\Big \Vert }&&&&&&&\\&-\infty &&&&&&&&&&-\infty &{\Big \Vert }&&&&&&&\\\hline \end{array}}$
Quand $t\to \pm \infty$ , $y-x={\frac {t^{2}-6t}{t^{2}-9}}\to 1$ donc asymptote $y=x+1$ .
Quand $t\to 3$ , $y-{\frac {2}{3}}x={\frac {t(t+6)}{3(t+3)}}\to {\frac {3}{2}}$ donc asymptote $y={\frac {2}{3}}x+{\frac {3}{2}}$ .
$M(0)=(0,0)$ est un point d'inflexion à tangente verticale.
On étudie $x={\frac {t^{3}}{1+3t}},y={\frac {3t^{2}}{1+3t}}$ pour $t\in \mathbb {R} \setminus \left\{-{\frac {1}{3}}\right\}$ .
$x'=3t^{2}{\frac {1+2t}{\left(1+3t\right)^{2}}},y'=3t{\frac {2+3t}{\left(1+3t\right)^{2}}}$ donc le point $\left(x,y\right)\left(0\right)=\left(0,0\right)$ est singulier (rebroussement de première espèce à tangente verticale car ${\frac {y}{x}}={\frac {3}{t}}$ ), et deux autres points remarquables sont $\left(x,y\right)\left(-{\frac {1}{2}}\right)=\left({\frac {1}{4}},-{\frac {3}{2}}\right)$ (tangente verticale), $\left(x,y\right)\left(-{\frac {2}{3}}\right)=\left({\frac {8}{27}},-{\frac {4}{3}}\right)$ (tangente horizontale).
$\left(x,y\right)\sim _{t\to \pm \infty }\left({\frac {t^{2}}{3}},t\right)$ donne deux branches paraboliques de direction horizontale.
Quand $t\to -{\frac {1}{3}}$ , $y+9x=3t^{2}\to {\frac {1}{3}}$ donne une asymptote $y=-9x+{\frac {1}{3}}$ .
La position de la courbe par rapport à cette asymptote est donnée par le signe de $y\left(t\right)-\left(-9x\left(t\right)+{\frac {1}{3}}\right)=3t^{2}-{\frac {1}{3}}={\frac {\left(3t-1\right)\left(3t+1\right)}{3}}$ , donc la courbe est en dessous si $-{\frac {1}{3}}<t<{\frac {1}{3}}$ et au-dessus sinon (en particulier : au-dessus pour les deux points remarquables correspondant à $t=-{\frac {1}{2}}$ et $t=-{\frac {2}{3}}$ ).
$x=t^{2}+t^{3}=t^{2}\left(1+t\right),y=t^{2}+t^{3}-2t^{4}-2t^{5}=x\left(1-2t^{2}\right)$ .
Deux branches paraboliques de direction verticale quand $t\to \pm \infty$ .
Point singulier avec rebroussement de deuxième espèce pour $t=0$ , avec tangente $y=x$ .
La courbe repasse par ce point $\left(0,0\right)$ pour $t=-1$ , avec tangente $y=-x$ .
La courbe est définie pour $t$ non nul et $>-\ln 2$ .
$x'>0$ , et $y'$ est du signe de $t$ . En calculant les limites aux bornes, on aboutit au tableau suivant, avec $\alpha ={\frac {1-\ln ^{2}2}{\ln 2}}>0$ :
${\begin{array}{|c|lcccccc|}\hline t&-\ln 2&&&0&&&+\infty \\\hline &&&+\infty &{\Big \Vert }&&&+\infty \\x&&\nearrow &&{\Big \Vert }&&\nearrow &\\&\alpha &&&{\Big \Vert }&-\infty &&\\\hline &+\infty &&&&&&+\infty \\y&&\searrow &&&&\nearrow &\\&&&&0&&&\\\hline \end{array}}$
La courbe a donc pour asymptotes l'axe des abscisses (quand $t\to 0^{\pm }$ , $y\to 0^{+}$ et $x\to \mp \infty$ ) et la verticale $x=\alpha$ (quand $t\to (-\ln 2)^{+}$ , $x\to \alpha ^{+}$ et $y\to +\infty$ ). La quatrième branche infinie est aussi asymtotique : quand $t\to +\infty$ , $2y-x=t-\ln(2\operatorname {e} ^{t}-1)+{\frac {1}{t}}=-\ln 2-\ln(1-\operatorname {e} ^{-t}/2)+{\frac {1}{t}}\to (-\ln 2)^{+}$ donc l'asymptote a pour équation $x=2y+\ln 2$ et la courbe est au-dessus.
$x'=2t-{\frac {2}{t^{2}}},\,y'=2t-{\frac {2}{t^{3}}}$ $x'=2t-{\frac {2}{t^{2}}},\,y'=2t-{\frac {2}{t^{3}}}$ .
${\begin{array}{|c|lcccccc|}\hline t&-\infty &&-1&&&0&&&1&&+\infty \\\hline &+\infty &&&&&{\Big \Vert }&+\infty &&&&+\infty \\&&\searrow &&&&{\Big \Vert }&&\searrow &&\nearrow &\\x&&&-1&&&{\Big \Vert }&&&3&&\\&&&&\searrow &&{\Big \Vert }&&&&&\\&&&&&-\infty &{\Big \Vert }&&&&&\\\hline &+\infty &&&&+\infty &{\Big \Vert }&+\infty &&&&+\infty \\y&&\searrow &&\nearrow &&{\Big \Vert }&&\searrow &&\nearrow &\\&&&2&&&{\Big \Vert }&&&2&&\\\hline \end{array}}$ ${\begin{array}{|c|lcccccc|}\hline t&-\infty &&-1&&&0&&&1&&+\infty \\\hline &+\infty &&&&&{\Big \Vert }&+\infty &&&&+\infty \\&&\searrow &&&&{\Big \Vert }&&\searrow &&\nearrow &\\x&&&-1&&&{\Big \Vert }&&&3&&\\&&&&\searrow &&{\Big \Vert }&&&&&\\&&&&&-\infty &{\Big \Vert }&&&&&\\\hline &+\infty &&&&+\infty &{\Big \Vert }&+\infty &&&&+\infty \\y&&\searrow &&\nearrow &&{\Big \Vert }&&\searrow &&\nearrow &\\&&&2&&&{\Big \Vert }&&&2&&\\\hline \end{array}}$
- Point singulier pour $t=1$ : $x(1+h)=3+3h^{2}-2h^{3}+o(h^{3}),\,y(1+h)=2+4h^{2}-4h^{3}+o(h^{3})$ .
  $M(1+h)=M(1)+h^{2}u+h^{3}v+o(h^{3})$ . Donc rebroussement de première espèce, vecteur tangent $u=(3,4)$ .
- Branches infinies quand $t\to \pm \infty$ : $y-x\sim _{t\to \pm \infty }{\frac {-2}{t}}$ . Courbe en-dessous de l'asymptote $y=x$ quand $t\to +\infty$ et au-dessus quand $t\to -\infty$ .
- Branches infinies quand $t\to 0^{\pm }$ : ${\frac {y}{x}}\sim _{t\to 0}{\frac {1}{t}}$ donc branches paraboliques de direction verticale. Plus précisément, $y-{\frac {x^{2}}{4}}\sim -t$ donc parabole asymptote $y=x^{2}$ , et courbe au-dessus quand $t\to 0^{-}$ et en dessous en $t\to 0^{+}$ .

Exercice 5

Soit un réel $R>0$ .

Trouver les trajectoires orthogonales à la famille des cercles de rayon $R$ et centrés sur $(Ox)$ .
Étudier et tracer la courbe paramétrée $x=R\left(\ln \left|\tan {\frac {t}{2}}\right|+\cos t\right),y=R\sin t$ .

Solution

Cherchons les solutions sous la forme $x=f(t)+R\cos t,\quad y=R\sin t$ . Au point $M(t)$ , la courbe est orthogonale au cercle (de centre $\Omega (t)=\left(f(t),0\right)$ et de rayon $R$ ) si et seulement si le vecteur dérivé $\left(x',y'\right)$ est colinéaire au rayon ${\overrightarrow {\Omega (t)M(t)}}$ , c'est-à-dire si $0={\begin{vmatrix}f'(t)-R\sin t&\cos t\\R\cos t&\sin t\end{vmatrix}}=f'(t)\sin t-R$ . Or une primitive de ${\frac {1}{\sin t}}$ est $\ln {\frac {|\sin t|}{1+\cos t}}=\ln \left|\tan {\frac {t}{2}}\right|$ (cf. Changement de variable en calcul intégral/Exercices/Changement de variable facile#Exercice 2-10). Les courbes solutions sont donc :
$x=R\left(\ln \left|\tan {\frac {t}{2}}\right|+\cos t\right)+C,\quad y=R\sin t$ .
On peut restreindre l'intervalle d'étude à $\left]-\pi ,0\right[\cup \left]0,\pi \right[$ par périodicité, puis à $\left]0,\pi \right[$ par symétrie par rapport à $(Ox)$ (via $t\mapsto -t$ ), puis à $\left]0,\pi /2\right]$ par symétrie par rapport à $(Oy)$ (via $t\mapsto \pi -t$ ). $\lim _{0^{+}}x=-\infty ,\quad \lim _{0^{+}}y=0^{+}$ , donc $Ox$ est asymptote. Sur $\left]0,\pi /2\right[$ , $x'(t)=R\left({\frac {1}{\sin t}}-\sin t\right)={\frac {\cos ^{2}t}{\sin t}}>0$ et $y'(t)=R\cos t>0$ , donc $x$ et $y$ sont croissantes et le vecteur $\left(x',y'\right)=R\cot t\left(\cos t,\sin t\right)$ s'annule pour $t={\frac {\pi }{2}}$ donc le point $M(\pi /2)=\left(0,R\right)$ est singulier. Pour étudier la courbe quand $t\to {\frac {\pi }{2}}$ , posons $t={\frac {\pi }{2}}+h$ avec $h\to 0$ . Ainsi, ${\frac {x}{R}}=\ln {\frac {\sin \left({\frac {\pi }{2}}+h\right)}{1+\cos \left({\frac {\pi }{2}}+h\right)}}+\cos \left({\frac {\pi }{2}}+h\right)=\ln {\frac {\cos h}{1-\sin h}}-\sin h=-{\frac {h^{2}}{2}}-\left(-\sin h-{\frac {1}{2}}\sin ^{2}h-{\frac {1}{3}}\sin ^{3}h\right)-\sin h+o\left(h^{3}\right)={\frac {1}{3}}\sin ^{3}h+o\left(h^{3}\right)\sim {\frac {h^{3}}{3}}$ et ${\frac {y-R}{R}}=\sin \left({\frac {\pi }{2}}+h\right)-1=\cos h-1\sim -{\frac {h^{2}}{2}}$ donc $M(\pi /2)$ est un point de rebroussement de première espèce, à demi-tangente verticale, dirigée vers le bas.

Voir aussi http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 1, question 5, ainsi que l'exercice 10 ci-dessous.

Exercice 6

En un point $M(t_{0})$ d'une courbe paramétrée, le rayon de courbure est donné par
$\rho (t_{0})={\frac {(x'(t_{0})^{2}+y'(t_{0})^{2})^{3/2}}{\vert x'(t_{0})y''(t_{0})-y'(t_{0})x''(t_{0})\vert }}$ et le centre de courbure est le point $\Omega (t_{0})$ qui est à distance $\rho (t_{0})$ de $M(t_{0})$ ,

tel que la droite $(\Omega (t_{0})M(t_{0}))$ est normale à la tangente $T_{t_{0}}$ , et placé dans l'intérieur de la courbe.

La développée est l'ensemble des centres de courbure.

Déterminer le rayon de courbure en tout point de :
1. l'astroïde $\left(x,y\right)=a\left(\cos ^{3}t,\sin ^{3}t\right)$ ;
2. la cycloïde $\left(x,y\right)=R\left(t-\sin t,1-\cos t\right)$ ;
3. la lemniscate $\left(x,y\right)=\left({\frac {t}{1+t^{4}}},{\frac {t^{3}}{1+t^{4}}}\right)$ .
Déterminer la développante de la cycloïde qui passe par le milieu d'une arche.
Déterminer la développée de l'ellipse d'équation ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ , dont la paramétrisation naturelle est donnée par
$x(\theta )=a\cos \theta ,\quad y(\theta )=b\sin \theta ,\quad \theta \in [0,2\pi ]$ .

Solution

$\rho ={\frac {\left(x^{\prime 2}+y^{\prime 2}\right)^{3/2}}{x'y''-y'x''}}$ $\rho ={\frac {\left(x^{\prime 2}+y^{\prime 2}\right)^{3/2}}{x'y''-y'x''}}$ .
1. Astroïde : $\left(x,y\right)=a\left(\cos ^{3}t,\sin ^{3}t\right)\Rightarrow \left(x',y'\right)=3a\cos t\sin t\left(-\cos t,\sin t\right)\Rightarrow$
  $x''=3a\left(2\cos t\sin ^{2}t-\cos ^{3}t\right)=3a\cos t\left(\cos ^{2}t-2\sin ^{2}t\right)=3a\cos t\left(1-3\sin ^{2}t\right)$ ,
  
  $y''=3a\left(2\sin t\cos ^{2}t-\sin ^{3}t\right)=3a\sin t\left(2\cos ^{2}t-\sin ^{2}t\right)=3a\sin t\left(3\cos ^{2}t-1\right)$ ,
  
  ${\sqrt {x^{\prime 2}+y^{\prime 2}}}=\left|3a\sin t\cos t\right|$ ,
  
  $x'y''-y'x''=9a^{2}\cos ^{2}t\sin ^{2}t\left(3\cos ^{2}t-1-1+3\sin ^{2}t\right)=\left(3a\cos t\sin t\right)^{2}$ ,
  
  $\rho ={\frac {1}{3a\left|\sin t\cos t\right|}}$ .
2. Cycloïde : $\left(x,y\right)=R\left(t-\sin t,1-\cos t\right)\Rightarrow \left(x',y'\right)=R\left(1-\cos t,\sin t\right)\Rightarrow \left(x'',y''\right)=R\left(\sin t,\cos t\right)$ ,
  $x^{\prime 2}+y^{\prime 2}=R^{2}\left(2-2\cos t\right)=4R^{2}\sin ^{2}{\frac {t}{2}}$ ,
  
  $x'y''-y'x''=R^{2}\left(\cos t\left(1-\cos t\right)-\sin ^{2}t\right)=R^{2}\left(\cos t-1\right)=-2R^{2}\sin ^{2}{\frac {t}{2}}$ ,
  
  $\rho =-4R\left|\sin {\frac {t}{2}}\right|$ .
3. Lemniscate $\left(x,y\right)=\left({\frac {t}{1+t^{4}}},{\frac {t^{3}}{1+t^{4}}}\right)\Rightarrow \left(x',y'\right)=\left({\frac {1-3t^{4}}{\left(1+t^{4}\right)^{2}}},{\frac {3t^{2}-t^{6}}{\left(1+t^{4}\right)^{2}}}\right)\Rightarrow$
  $x''={\frac {-12t^{3}\left(1+t^{4}\right)-8t^{3}\left(1-3t^{4}\right)}{\left(1+t^{4}\right)^{3}}}={\frac {4t^{3}\left(3t^{4}-5\right)}{\left(1+t^{4}\right)^{3}}}$ ,
  
  $y''={\frac {6t\left(1-t^{8}\right)-8t^{5}\left(3-t^{4}\right)}{\left(1+t^{4}\right)^{3}}}={\frac {2t\left(3-12t^{4}+t^{8}\right)}{\left(1+t^{4}\right)^{3}}}$ ,
  
  $x^{\prime 2}+y^{\prime 2}={\frac {\left(1-3t^{4}\right)^{2}+\left(3t^{2}-t^{6}\right)^{2}}{\left(1+t^{4}\right)^{4}}}={\frac {1+3t^{4}+3t^{8}+t^{12}}{\left(1+t^{4}\right)^{4}}}={\frac {1}{1+t^{4}}}$ ,
  
  ${\begin{aligned}x'y''-y'x''&={\frac {2t}{\left(1+t^{4}\right)^{5}}}\left(\left(1-3t^{4}\right)\left(3-12t^{4}+t^{8}\right)-2t^{4}\left(3t^{4}-5\right)\left(3t^{4}-5\right)\right)\\&={\frac {2t}{\left(1+t^{4}\right)^{5}}}\left(3+9t^{4}+9t^{8}+3t^{12}\right)^{3}={\frac {6t}{\left(1+t^{4}\right)^{2}}}\end{aligned}}$ ,
  
  $\rho ={\frac {\sqrt {1+t^{4}}}{6t}}$ . Remarque : $\rho ^{2}={\frac {1}{6\left(x^{2}+y^{2}\right)}}$ .
Prenons, comme origine de l'abscisse curviligne $s(t)$ , le point $M(\pi )$ (sommet de la première arche) et étudions la développante pour $\pi <t<2\pi$ (donc $\sin {\frac {t}{2}}>0$ et $\cos {\frac {t}{2}}<0$ ). Elle est paramétrée par
$N=M-s{\overrightarrow {T}}$ avec, puisque $\left(x',y'\right)=2R\sin {\frac {t}{2}}\left(\sin {\frac {t}{2}},\cos {\frac {t}{2}}\right)$ :

${\overrightarrow {T}}(t)=\left(\sin {\frac {t}{2}},\cos {\frac {t}{2}}\right)$ et $s(t)=\int _{\pi }^{t}2R\sin {\frac {u}{2}}\,\mathrm {d} u=-4R\cos {\frac {t}{2}}$ , donc

$N(t)=R\left(t-\sin t,1-\cos t\right)+4R\cos {\frac {t}{2}}\left(\sin {\frac {t}{2}},\cos {\frac {t}{2}}\right)=R\left(t+\sin t,3+\cos t\right)$ .

Par translation temporelle et spatiale, on retrouve donc la même cycloïde :

$N(\pi +h)=R\left(\pi +h-\sin h,3-\cos h\right)=\left(\pi R,2R\right)+R\left(h-\sin h,1-\cos h\right)$ .
$\rho (\theta )={\frac {\left((-a\sin \theta )^{2}+(b\cos \theta )^{2}\right)^{3/2}}{ab\sin ^{2}\theta +ab\cos ^{2}\theta }}={\frac {\left(a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta \right)^{3/2}}{ab}}$
et un vecteur unitaire normal pointant vers l'intérieur est $(-b\cos \theta ,-a\sin \theta )/{\sqrt {a^{2}s^{2}+b^{2}c^{2}}}$ ,

donc $\Omega (\theta )$ a pour coordonnées :
$x_{\Omega }(\theta )=a\cos \theta -{\frac {a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta }{ab}}b\cos \theta ={\frac {a^{2}-b^{2}}{a}}\cos ^{3}\theta$ ,

$y_{\Omega }(\theta )=b\sin \theta -{\frac {a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta }{ab}}a\sin \theta ={\frac {b^{2}-a^{2}}{b}}\sin ^{3}\theta$ .

Ceci constitue une paramétrisation de la développée de l'ellipse.

Exercice 7

1. Trouver les droites à la fois tangentes et normales à la courbe paramétrée $x=3t^{2},y=4t^{3}$ .

Solution

Cherchons $t_{1},t_{2}$ distincts et non nuls (on examinera à part le point singulier) tels que la tangente en $M(t_{1})$ soit normale en $M(t_{2})$ , c'est-à-dire tels que ${\overrightarrow {M(t_{1})M(t_{2})}}$ soit colinéaire à $\left(x'(t_{1}),y'(t_{1})\right)$ et orthogonal à $\left(x'(t_{2}),y'(t_{2})\right)$ .

$\left(x',y'\right)=6t\left(1,2t\right)$ donc la condition est :

${\begin{vmatrix}3\left(t_{2}^{2}-t_{1}^{2}\right)&1\\4\left(t_{2}^{3}-t_{1}^{3}\right)&2t_{1}\end{vmatrix}}=0$ et $1^{2}+\left(2t_{1}\right)\left(2t_{2}\right)=0$ , ce qui équivaut (en simplifiant la première équation par $t_{2}-t_{1}$ ) à

$6t_{1}\left(t_{2}+t_{1}\right)-4\left(t_{2}^{2}+t_{1}t_{2}+t_{1}^{2}\right)=0$ et $t_{1}t_{2}=-{\frac {1}{4}}$ , ou encore :

$t_{2}=-{\frac {1}{4t_{1}}}$ et $t_{1}^{2}-{\frac {1}{8t_{1}^{2}}}={\frac {1}{4}}$ .

$t_{1}^{2}$ est la solution positive de l'équation $x^{2}-{\frac {1}{8}}={\frac {x}{4}}$ , c'est-à-dire $t_{1}^{2}={\frac {1}{2}}$ .

Variante : cherchons $t_{1},t_{2}$ distincts et non nuls tels que la tangente en $M(t_{1})$ , d'équation $0={\begin{vmatrix}x-3t_{1}^{2}&1\\y-4t_{1}^{3}&2t_{1}\end{vmatrix}}=2t_{1}x-y-2t_{1}^{3}$ , soit égale à la normale en $M(t_{2})$ , d'équation $0=\langle {\begin{pmatrix}x-3t_{2}^{2}\\y-4t_{2}^{3}\end{pmatrix}},{\begin{pmatrix}1\\2t_{2}\end{pmatrix}}\rangle =x+2t_{2}y-3t_{2}^{2}-8t_{2}^{4}$ . Ces deux équations représentent la même droite si et seulement si les deux triplets de coefficients $\left(2t_{1},-1,-2t_{1}^{3}\right)$ et $\left(1,2t_{2},-3t_{2}^{2}-8t_{2}^{4}\right)$ sont proportionnels, c'est-à-dire (en simplifiant la deuxième équation par $2t_{1}$ ) :

$-1=2t_{1}\times 2t_{2}$ et $t_{1}^{2}=3t_{2}^{2}+8t_{2}^{4}$ , ou encore :

$t_{1}=-{\frac {1}{4t_{2}}}$ et ${\frac {1}{4^{2}t_{2}^{2}}}=3t_{2}^{2}+8t_{2}^{4}$ .

$t_{2}^{2}$ est une racine positive du polynôme $8x^{3}+3x^{2}-{\frac {1}{16}}=\left(8x-1\right)\left(x+{\frac {1}{4}}\right)^{2}$ , donc $t_{2}^{2}={\frac {1}{8}}$ .

Finalement, que ce soit par la première méthode ou par la variante, il y a donc deux solutions : $\left(t_{1},t_{2}\right)=\varepsilon \left({\frac {1}{\sqrt {2}}},-{\frac {1}{2{\sqrt {2}}}}\right)$ avec $\varepsilon =\pm 1$ , d'où $M(t_{1})=\left({\frac {3}{2}},\varepsilon {\sqrt {2}}\right)$ , $M(t_{2})=\left({\frac {3}{8}},-{\frac {\varepsilon }{4{\sqrt {2}}}}\right)$ et les deux droites (symétriques par rapport à $(Ox)$ , comme la courbe) ont pour équation : $0={\begin{vmatrix}x-{\frac {3}{2}}&1\\y-\varepsilon {\sqrt {2}}&\varepsilon {\sqrt {2}}\end{vmatrix}}=\varepsilon {\sqrt {2}}\left(x-{\frac {1}{2}}\right)-y$ .

Examinons maintenant le point singulier $t=0$ , $x=y=0$ (rebroussement de première espèce). La tangente et la normale ce point sont $(Ox)$ et $(Oy)$ , qui ne touchent la courbe qu'en ce point donc ne donnent pas de solution supplémentaire.

Zoomer sur l'image.

2. La normale en un point M de la parabole $x=y^{2}$ recoupe cette parabole en N. La parallèle en M à la tangente en N coupe en un point P la parallèle en N à la tangente en M. Déterminer le lieu de P et le tracer.

Solution

Notons respectivement $(x,y)$ , $(x',y')$ et $(x'',y'')$ les coordonnées de M, N et P.

N se déduit de M par :

0=2y(x'-x)+1(y'-y)=(y'-y)(2y(y'+y)+1)

donc

y'=-{\frac {1}{2y}}-y\quad {\text{et}}\quad x'={y'}^{2}={\frac {1}{4y^{2}}}+1+y^{2}

.

Puis P s'en déduit par :

x''-x'=2y(y''-y')\quad {\text{et}}\quad x''-x=2y'(y''-y)

soit

x'+2yy''=x''+2yy'=x+2y'y''

donc

y''={\frac {x'-x}{2(y'-y)}}={\frac {y'+y}{2}}=-{\frac {1}{4y}}

et

x''=x'+2y(y''-y')={\frac {1}{4y^{2}}}+1+y^{2}+2y(-{\frac {1}{4y}}+{\frac {1}{2y}}+y)={\frac {1}{4y^{2}}}+{\frac {3}{2}}+3y^{2}

.

Le lieu de P est donc la courbe d'équation

x''=4{y''}^{2}+{\frac {3}{2}}+{\frac {3}{16{y''}^{2}}}

. Tracé par google.

Exercice 8

L'orthoptique d'une courbe ${\mathcal {C}}$ est le lieu des points du plan d'où l'on peut mener (au moins) deux tangentes à ${\mathcal {C}}$ , orthogonales. Soient $a,b>0$ . Déterminer l'orthoptique de :

l'astroïde $x=a\cos ^{3}t,y=a\sin ^{3}t$ ;
la courbe $x=t^{2}-2t,y=2t^{3}-3t^{2}$ ;
l'ellipse d'équation ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ . (Indication : étant donné un point $M_{0}(x_{0},y_{0})$ , chercher la condition sur $m$ pour que la droite passant par $M_{0}$ et de coefficient directeur $m$ soit tangente à l'ellipse.)

Solution

L'orthoptique d'une astroïde est un quadrifolium.

1°) http://exo7.emath.fr/ficpdf/fic00112.pdf exercice 3, question 1 : $2\left(x^{2}+y^{2}\right)^{3}=a^{2}\left(x^{2}-y^{2}\right)^{2}$ .

2°) $\left(x,y\right)=\left(t^{2}-2t,2t^{3}-3t^{2}\right)\Rightarrow \left(x',y'\right)=\left(2t-2,6t^{2}-6t\right)=\left(2t-2\right)\left(1,3t\right)$ donc la tangente a pour pente $3t$ .

Cela est encore valable au point singulier

t=1

car en posant

t=1+h

, on trouve

\left(x,y\right)=\left(-1+h^{2},-1+3h^{2}+2h^{3}\right)

.

Si

t\neq 0

, une tangente orthogonale aura pour pente

3t'=-1/(3t)

. Calculons le point d'intersection des tangentes (orthogonales) aux points

M(t)

et

M(t')

, pour

t\in \mathbb {R} ^{*}

et

t'=-{\frac {1}{9t}}

.

La première tangente a pour équation :

y-2t^{3}+3t^{2}=3t(x-t^{2}+2t)\Leftrightarrow y-3tx=-t^{3}+3t^{2}\Leftrightarrow y-sx=-s^{3}/27+s^{2}/3

, en posant

3t=s

pour simplifier les notations, donc

3t'=-1/s

.

Le point d'intersection vérifie donc :

{\begin{cases}y-sx&=-{\frac {s^{3}}{27}}+{\frac {s^{2}}{3}}\\y+{\frac {x}{s}}&={\frac {1}{27s^{3}}}+{\frac {1}{3s^{2}}}\end{cases}}\Leftrightarrow {\begin{cases}\left({\frac {1}{s}}+s\right)x&={\frac {1}{27}}\left({\frac {1}{s^{3}}}+s^{3}\right)+{\frac {1}{3}}\left({\frac {1}{s^{2}}}-s^{2}\right)\\\left({\frac {1}{s}}+s\right)y&={\frac {1}{27}}\left({\frac {1}{s^{2}}}-s^{2}\right)+{\frac {1}{3}}\left({\frac {1}{s}}+s\right)\end{cases}}\Leftrightarrow {\begin{cases}x&={\frac {1}{27}}\left({\frac {1}{s^{2}}}-1+s^{2}\right)+{\frac {1}{3}}\left({\frac {1}{s}}-s\right)\\y&={\frac {1}{27}}\left({\frac {1}{s}}-s\right)+{\frac {1}{3}}\end{cases}}\Leftrightarrow {\begin{cases}x&={\frac {u^{2}+1}{27}}+{\frac {u}{3}}\\y&={\frac {u}{27}}+{\frac {1}{3}}\end{cases}}

avec comme nouveau paramètre

u={\frac {1}{s}}-s\in \mathbb {R}

. On a ainsi paramétré la courbe orthoptique.

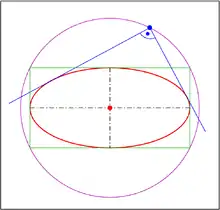
L'orthoptique d'une ellipse est un cercle.

3°) Une droite de pente $m$ passant par un point $\left(x_{0},y_{0}\right)$ a pour équation $y=y_{0}+m\left(x-x_{0}\right)$ donc un point $\left(x,y\right)$ de cette droite appartient à l'ellipse si et seulement si

b^{2}x^{2}+a^{2}\left(y_{0}+m\left(x-x_{0}\right)\right)^{2}=a^{2}b^{2}

,

ce qui se réécrit

\left(b^{2}+a^{2}m^{2}\right)x^{2}+2a^{2}m\left(y_{0}-mx_{0}\right)x+a^{2}\left[\left(y_{0}-mx_{0}\right)^{2}-b^{2}\right]=0

.

La droite est tangente à l'ellipse si cette équation en

x

a une racine double, c'est-à-dire si son discriminant est nul.

{\begin{aligned}\Delta '&=a^{4}m^{2}\left(y_{0}-mx_{0}\right)^{2}-a^{2}\left(b^{2}+a^{2}m^{2}\right)\left[\left(y_{0}-mx_{0}\right)^{2}-b^{2}\right]\\&=a^{2}\left[a^{2}m^{2}\left(y_{0}-mx_{0}\right)^{2}-\left(b^{2}+a^{2}m^{2}\right)\left(y_{0}-mx_{0}\right)^{2}+\left(b^{2}+a^{2}m^{2}\right)b^{2}\right]\\&=a^{2}b^{2}\left[\left(b^{2}+a^{2}m^{2}\right)-\left(y_{0}-mx_{0}\right)^{2}\right]\end{aligned}}

Donc

\Delta '=0\Leftrightarrow \left(a^{2}-x_{0}^{2}\right)m^{2}+2x_{0}y_{0}m+b^{2}-y_{0}^{2}=0

.

Lorsque $x_{0}\neq \pm a$ , cette équation en $m$ a deux solutions complexes. Le point $\left(x_{0},y_{0}\right)$ appartient alors à l'orthoptique de l'ellipse si et seulement si ces deux solutions ont pour produit $-1$ (ce qui implique qu'elles sont réelles et distinctes), c'est-à-dire si $b^{2}-y_{0}^{2}=-\left(a^{2}-x_{0}^{2}\right)$ , ou encore :
$x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}$ .
Lorsque $x_{0}=\pm a$ , l'une des deux tangentes à l'ellipse issues de $\left(x_{0},y_{0}\right)$ est verticale, donc l'autre lui est orthogonale si et seulement si $y_{0}=\pm b$ , ce qui, à nouveau, équivaut à $x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}$ .

L'orthoptique de l'ellipse est donc le cercle d'équation

x^{2}+y^{2}=a^{2}+b^{2}

.

« Orthoptique », sur mathcurve.com

Exercice 9

Soit ${\mathcal {C}}$ le cercle de centre $O=\left(0,0\right)$ et de rayon $R$ .

Donner un paramétrage de la développante $\Gamma$ de ${\mathcal {C}}$ passant par le point $\left(R,0\right)$ .
Soit $\Gamma '$ $\Gamma '$ la translatée de $\Gamma$ $\Gamma$ par le vecteur $\left(0,2\pi R\right)$ $\left(0,2\pi R\right)$ . Justifier que :
- $\Gamma$ et $\Gamma '$ sont tangentes ;
- le point de tangence appartient à l'axe vertical $T$ d'équation $x=R$ .
- la tangente est horizontale.
Soit $\Gamma ''$ la courbe symétrique de $\Gamma '$ par rapport à $T$ . Justifier que $\Gamma$ et $\Gamma ''$ sont tangentes.
Quel est l'intérêt mécanique de cette propriété ?

Solution

$\left(x,y\right)=R\left(\cos t+t\sin t,\sin t-t\cos t\right)$ .
Ces trois conditions sont réunies en un point $M(t)\in \Gamma$ $M(t)\in \Gamma$ égal à un point $M(u)+\left(0,2\pi R\right)\in \Gamma '$ $M(u)+\left(0,2\pi R\right)\in \Gamma '$ si et seulement si :
- $\cos t+t\sin t=\cos u+u\sin u=1$ ;
- $\sin t-t\cos t=\sin u-u\cos u+2\pi$ ;
- $t\sin t=u\sin u=0$ ,
c.-à-d. : $u=2k\pi$ et $t=2\left(k-1\right)\pi$ , $k\in \mathbb {Z}$ . Le point de tangence est alors : $R\left(1,-t\right)$ .
Ce point de tangence appartient à $T$ donc à $\Gamma ''$ , et la tangente en ce point à $\Gamma ''$ est la même que la tangente à $\Gamma '$ , puisque cette dernière est horizontale donc égale à sa symétrique par rapport à $T$ .
Cette propriété permet de réaliser des engrenages : voir l'article de Wikipédia.

Exercice 10

Soit un réel $a>0$ . On note :

$T$ l'intersection de $(Ox)$ et de la tangente en $M$ ;
$H$ le projeté orthogonal de $M$ sur $(Ox)$ .

Trouver les courbes telles que $HT=a$ ;
Trouver les courbes telles que $MT=a$ .

Solution

La tangente en $M(t)=\left(x(t),y(t)\right)$ a pour équation $\left(x-x(t)\right)y'(t)=\left(y-y(t)\right)x'(t)$ donc $T(t)$ a pour abscisse $x(t)-{\frac {y(t)}{y'(t)}}x'(t)$ .

Les sous-tangentes HT d'une courbe exponentielle ont toutes même longueur.

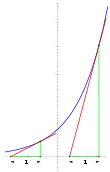
1. $HT=a\Leftrightarrow \left|{\frac {y}{y'}}x'\right|=a$ donc $y$ ne s'annule pas, et l'on peut se restreindre aux courbes telles que $y>0$ (les courbes telles que $y<0$ seront leurs symétriques par rapport à $(Ox)$ ). Il est commode de choisir $t=y$ comme paramètre (donc $t>0$ ) car l'équation différentielle se simplifie alors en

x'(t)=\pm {\frac {a}{t}}

,

dont la solution est : $x=\pm a\ln t+C,\quad y=t$ , ou encore :

y=\exp \left(\pm {\frac {x-C}{a}}\right)

.

Il était dès le départ prévisible que l'ensemble des courbes solutions est invariant, en plus de la symétrie par rapport à $(Ox)$ déjà mentionnée, par translations horizontales et par symétries par rapport aux verticales, et il en sera de même dans la question suivante.

2. $MT=a\Leftrightarrow \left({\frac {y}{y'}}x'\right)^{2}+y^{2}=a^{2}$ . On peut, comme dans la première question, supposer $y>0$ . Il est plus commode ici de choisir $t={\frac {y}{a}}$ comme paramètre (donc, à nouveau, $t>0$ ) car l'équation différentielle devient ainsi

a^{2}t^{2}+\left(tx'\right)^{2}=a^{2}

,

ce qui équivaut à

x'(t)=\pm a\,{\frac {\sqrt {1-t^{2}}}{t}}

.

Justification du nom « tractrice » pour la courbe d'équation MT = constante.

On est dans le deuxième cas d'une intégrale contenant une racine carrée d'un polynôme du second degré.

Méthode avec la trigonométrie circulaire :

On peut poser $u=\arccos t\in \left[0,\pi /2\right[$ donc $\sin u\geq 0,\quad t=\cos u,\quad \mathrm {d} t=-\sin u\,\mathrm {d} u$ ,

$\int {\frac {\sqrt {1-t^{2}}}{t}}\,\quad \mathrm {d} t=\int {\frac {-\sin ^{2}u}{\cos u}}\,\mathrm {d} u=\int \left(\cos u-{\frac {1}{\cos u}}\right)\,\mathrm {d} u$ .

Or sur $\left]-\pi /2,\pi /2\right[$ , une primitive de ${\frac {1}{\cos u}}$ est $\ln {\frac {1+\sin u}{\cos u}}=\ln \tan {\frac {u+\pi /2}{2}}$ (voir Changement de variable en calcul intégral/Exercices/Changement de variable facile#Exercice 2-10).

Donc $\int {\frac {\sqrt {1-t^{2}}}{t}}\,\quad \mathrm {d} t=\left[\sin u+\ln {\frac {\cos u}{1+\sin u}}\right]$ et la solution est :

x=\pm a\left(\sin u+\ln {\frac {\cos u}{1+\sin u}}\right)+C,\quad y=a\cos u

,

ou encore, en posant $v=u+{\frac {\pi }{2}}$ :

x=\mp a\left(\cos v+\ln \tan {\frac {v}{2}}\right)+C,\quad y=a\sin v

.

On reconnaît ainsi la courbe étudiée dans l'exercice 5 (voir supra).

Méthode avec la trigonométrie hyperbolique :

On peut poser $t={\frac {1}{\cosh u}},\quad \mathrm {d} t=-{\frac {\sinh u}{\cosh ^{2}u}}\,\mathrm {d} u$ ,

$\int {\frac {\sqrt {1-t^{2}}}{t}}\,\quad \mathrm {d} t=\int {\frac {-\sinh ^{2}u}{\cosh ^{2}u}}\,\mathrm {d} u=\int \left(1-{\frac {1}{\cosh ^{2}u}}\right)\,\mathrm {d} u=\left[u-\tanh u\right]$ et la solution est :

$x=\pm a\left(u-\tanh u\right)+C,\quad y={\frac {a}{\cosh u}}$ .

Exercice 11

Tracer la courbe d'équation polaire $r=a\left(1+\cos \theta \right)$ .

Solution

La cardioïde comme épicycloïde (ici, l'origine du repère est le centre du cercle fixe).

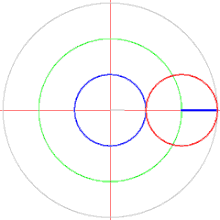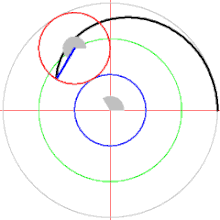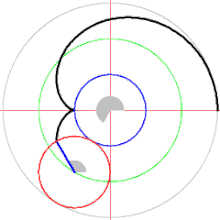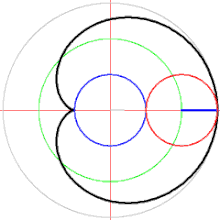
http://exo7.emath.fr/ficpdf/fic00113.pdf exercice 3, question 1.

Remarque : cette courbe est la trajectoire d'un point fixé à un cercle de diamètre $a=2R$ qui roule sans glisser sur un second cercle de même diamètre et de centre $\left(R,0\right)$ . En effet :

R+2R\cos \theta +R\cos \left(2\theta \right)=2R\left(1+\cos \theta \right)\cos \theta

;

2R\sin \theta +R\sin \left(2\theta \right)=2R\left(1+\cos \theta \right)\sin \theta

.

Exercice 12

Soit $\Gamma$ une spirale logarithmique, c'est-à-dire une courbe d'équation polaire $r=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}$ ( $k\in \mathbb {R} ^{*},\theta _{0}\in \mathbb {R}$ ).

Soit $M\in \Gamma$ . Que dire de l'angle $\alpha$ entre $(OM)$ et la tangente à $\Gamma$ en $M$ ? Montrer que cette propriété caractérise les spirales logarithmiques.
Calculer l'abscisse curviligne le long de $\Gamma$ .
En déduire qu'on peut former un engrenage avec deux spirales logarithmiques isométriques.
Si l'on fait rouler une spirale logarithmique sur une droite, quelle est la trajectoire du centre ?

Solution

L'angle entre le rayon et la tangente est constant.

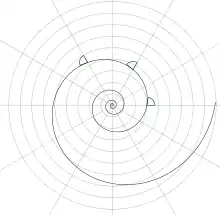
${\overrightarrow {OM}}=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}{\overrightarrow {u}}(\theta )\Rightarrow {\frac {\mathrm {d} {\overrightarrow {OM}}}{\mathrm {d} \theta }}=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}\left(k{\overrightarrow {u}}(\theta )+{\overrightarrow {u}}(\theta +\pi /2)\right)\Rightarrow \tan \alpha ={\frac {1}{k}}$ donc l'angle $\alpha$ est constant et non nul. Réciproquement, si ${\overrightarrow {OM}}=f(\theta ){\overrightarrow {u}}(\theta )$ avec ${\frac {f}{f'}}=\tan \left({\overrightarrow {OM}},{\frac {\mathrm {d} {\overrightarrow {OM}}}{\mathrm {d} \theta }}\right)={\frac {1}{k}}$ pour un certain $k\in \mathbb {R} ^{*}$ alors $f(\theta )=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}$ (avec $\theta _{0}\in \mathbb {R}$ ).
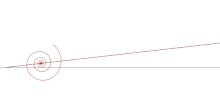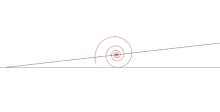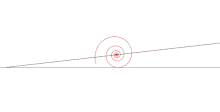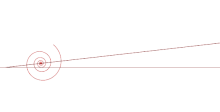$s'(\theta )=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}{\sqrt {1+k^{2}}}$ donc $s(\theta )=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}{\frac {\sqrt {1+k^{2}}}{k}}$ (en convenant que l'abscisse curviligne est nulle au centre, c'est-à-dire pour $\theta \to -\infty$ si $k>0$ et pour $\theta \to +\infty$ si $k<0$ ).
Quand la spirale roule sur une droite, son centre décrit une droite.
Si l'on enroule une spirale de caractéristique $k$ (autour de son centre) et qu'on déroule une spirale de même caractéristique (autour d'un autre centre) en gardant le contact en un point qui circule sur le segment qui joint leurs centres, alors les spirales restent tangentes (question 1) et sans glissement (question 2). Voir l'animation sur mathcurve.
Faisons rouler la spirale par exemple sur l'axe $(Ox)$ , en plaçant au départ son centre en $O$ . Lorsque ce centre a pour abscisse $x=s$ , il a pour ordonnée $y$ sa distance au point de contact donc $y=\operatorname {e} ^{k\left(\theta -\theta _{0}\right)}={\frac {k}{\sqrt {1+k^{2}}}}\,x$ : le centre de la spirale se déplace sur une droite.

Exercice 13

On considère un point mobile $M$ de vitesse ${\vec {v}}:={\frac {\mathrm {d} {\vec {M}}}{\mathrm {d} t}}$ et d'accélération ${\vec {a}}:={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}$ non colinéaires. On note $v:=\|v\|$ , ${\vec {T}}:={\frac {\vec {v}}{v}}$ et $s$ l'abscisse curviligne ( ${\frac {\mathrm {d} s}{\mathrm {d} t}}=v$ ).

Exprimer ${\vec {a}}$ comme combinaison linéaire de ${\vec {T}}$ et ${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}$ .
En déduire que ${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}\neq {\vec {0}}$ , et démontrer que ${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}\perp {\vec {T}}$ .
En déduire qu'il existe un vecteur unitaire ${\vec {N}}\perp {\vec {T}}$ et un réel $R\neq 0$ (rayon de courbure) tels que ${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}={\frac {1}{R}}{\vec {N}}$ .
Exprimer ${\vec {a}}$ comme combinaison linéaire de ${\vec {T}}$ et ${\vec {N}}$ .
On pose ${\vec {B}}={\vec {T}}\land {\vec {N}}$ (produit vectoriel). Démontrer que $({\vec {T}},{\vec {N}},{\vec {B}})$ est une base orthonormée directe.

Solution

${\vec {a}}={\frac {\mathrm {d} }{\mathrm {d} t}}\left(v{\vec {T}}\right)=v{\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} t}}+{\frac {\mathrm {d} v}{\mathrm {d} t}}{\vec {T}}=v^{2}{\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}+{\frac {\mathrm {d} v}{\mathrm {d} t}}{\vec {T}}$ .
${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}$ est donc non nul car sinon, ${\vec {a}}$ serait colinéaire à ${\vec {T}}$ donc à ${\vec {v}}$ .
$\|{\vec {T}}\|^{2}=1\Rightarrow 2{\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}\cdot {\vec {T}}=0\Rightarrow {\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}\perp {\vec {T}}$ .
On peut définir $R$ comme l'inverse de la norme de ${\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}$ , puis poser ${\vec {N}}:=R{\frac {\mathrm {d} {\vec {T}}}{\mathrm {d} s}}$ . Remarquons que $(-R,-{\vec {N}})$ convient également.
D'après les questions 1 et 3, ${\vec {a}}={\frac {\mathrm {d} v}{\mathrm {d} t}}{\vec {T}}+{\frac {v^{2}}{R}}{\vec {N}}$ .
$\|{\vec {N}}\|=\|{\vec {T}}\|=1$ , ${\vec {N}}\perp {\vec {T}}$ et ${\vec {B}}={\vec {T}}\land {\vec {N}}$ .

Exercice 14

Représenter graphiquement la parabole ${\displaystyle \Gamma$ .
Calculer l'équation cartésienne et l'équation paramétrique de la tangente à $\Gamma$ au point $(2,2)$ .

Solution

Tracé Google
En tout point $M(y):=(y^{2}/2,y)\in \Gamma$ , un vecteur tangent à $\Gamma$ est $M'(y)=(y,1)$ . La droite passant par $M(2)=(2,2)$ et dirigée par $M'(2)=(2,1)$ a pour équation cartésienne $0={\begin{vmatrix}x-2&2\\y-2&1\end{vmatrix}}=x-2y+2$ et pour équation paramétrique $x=2+2t,\,y=2+t$ .

Exercice 15

En quels points la courbe d'équation $(y-x^{2})^{2}+x^{2}=1$ a-t-elle une tangente parallèle à l'axe des $x$ ou celui des $y$ ?
À partir de ces informations, dessiner l'allure de la courbe.

Solution

En tout point $(x,y)$ de cette courbe d'équation $f(x,y)=0$ , un vecteur normal est $\operatorname {grad} f=2(x(-2(y-x^{2})+1),y-x^{2})$ .
Par conséquent, la tangente est est parallèle à l'axe des $y$ si $y=x^{2}$ (donc $(x,y)=(\pm 1,1)$ ), et à l'axe des $x$ si $x=0$ ou $y-x^{2}=1/2$ (donc $(x,y)=(0,\pm 1)$ ou $(\pm {\sqrt {3}}/2,5/4)$ ).
Tracé Google

Exercice 16

Dans les quatre cas suivants, trouver une paramétrisation rationnelle de la courbe :

$x\left(y^{2}-x^{2}\right)=2y^{2}-x^{2}$ ;
$\left(x^{2}+y^{2}\right)^{2}=x^{2}-y^{2}$ (lemniscate de Bernoulli) ;
$x^{3}+y^{3}=3xy$ (folium de Descartes) ;
$x^{3}-y^{3}+xy-2x+2y+3=0$ .

Solution

En posant $t={\frac {y}{x}}$ , l'équation équivaut à $x^{3}(t^{2}-1)=x^{2}(2t^{2}-1)$ .
La courbe est donc paramétrable par : $x={\frac {2t^{2}-1}{t^{2}-1}},\quad y={\frac {t(2t^{2}-1)}{t^{2}-1}}$ .
En posant $t={\frac {y}{x}}$ , l'équation équivaut à $x^{4}\left(1+t^{2}\right)^{2}=x^{2}\left(1-t^{2}\right)$ .
La courbe est donc paramétrable par : $\left(x,y\right)=\pm {\frac {\sqrt {1-t^{2}}}{1+t^{2}}}\left(1,t\right)$ .
En posant $t={\frac {y}{x}}$ , l'équation équivaut à $x^{3}\left(1+t^{3}\right)^{2}=3x^{2}t$ .
La courbe est donc paramétrable par : $x={\frac {3t}{1+t^{3}}},\quad y={\frac {3t^{2}}{1+t^{3}}}$ . Gerard Eguether, « Étude et tracé du folium de Descartes », 2012
Le seul point singulier étant $(1,-1)$ , posons $u=x-1$ et $v=y+1$ .
L'équation équivaut alors à $u^{3}-v^{3}+3u^{2}+3v^{2}+uv=0$ , soit, en posant $t={\frac {v}{u}}$ : $u^{3}(1-t^{3})+u^{2}(3+3t^{2}+t)=0$ .
La courbe est donc paramétrable par : $x=1+{\frac {3+3t^{2}+t}{t^{3}-1}},\quad y=-1+{\frac {t(3+3t^{2}+t)}{t^{3}-1}}$ .

Exercice 17

Étude locale.

Déterminez la nature, au point correspondant à la valeur $t=0$ $t=0$ du paramètre, des courbes paramétrées suivantes :
1. $t\mapsto (t+2t^{2}-t^{3},t+2t^{2}-t^{7})$ ;
2. $t\mapsto (-t+t^{2},t^{2}+t^{3})$ ;
3. $t\mapsto (t^{2}+3t^{3}+t^{4},-2t^{2}-6t^{3}+t^{4})$ ;
4. $t\mapsto (-t^{2}-2t^{3},-t^{3}-t^{5})$ .
Déterminez les points d'inflexion de la courbe $t\mapsto ((t-2)^{3},t^{2}-4)$ .

Solution

1. $\gamma '(t)=(1+4t-3t^{2},1+4t-7t^{6}),\;\gamma ''(t)=(4-6t,4-42t^{5}),\;\gamma '''(t)=(-6,-210t^{4})$ donc $\gamma '(0)=(1,16),\;\gamma ''(0)=4\gamma '(0),\;\gamma '''(0)=(-6,0)$ et $\gamma (0)$ est un point d'inflexion (car $p=1,q=3$ ).
2. $\gamma '(t)=(-1+2t,2t+3t^{2}),\;\gamma ''(t)=(2,2+6t)$ donc $\gamma '(0)=(-1,0),\;\gamma ''(0)=(2,2)$ et $\gamma (0)$ est un point ordinaire (car $p=1,q=2$ ).
3. $\gamma '(t)=(2t+9t^{2}+4t^{3},-4t-18t^{2}+4t^{3}),\;\gamma ''(t)=(2+18t+12t^{2},-4-36t+12t^{2}),\;\gamma '''(t)=(18+24t,-36+24t),\;\gamma ^{(4)}(t)=(24,24)$ donc $\gamma '(0)={\vec {0}},\;\gamma ''(0)=(2,-4),\;\gamma '''(0)=9\gamma ''(0),\;\gamma ^{(4)}(0)=(24,24)$ et $\gamma (0)$ est un point de rebroussement de deuxième espèce (car $p=2,q=4$ ).
4. $\gamma '(t)=(-2t-6t^{2},-3t^{2}-5t^{4}),\;\gamma ''(t)=(-2-12t,-6t-20t^{3}),\;\gamma '''(t)=(-12,-6-60t^{2})$ donc $\gamma '(0)={\vec {0}},\;\gamma ''(0)=(-2,0),\;\gamma '''(0)=(-12,-6)$ et $\gamma (0)$ est un point de rebroussement de première espèce (car $p=2,q=3$ ).
$\forall t\quad \gamma '(t)=(3(t-2)^{2},2t)\neq {\vec {0}}$ donc $p=1$ . $\gamma ''(t)=(6(t-2),2)$ est colinéaire à $\gamma '(t)$ si et seulement si $3(t-2)^{2}=6(t-2)t$ , c.-à-d. $t=\pm 2$ . $\gamma '''(\pm 2)=(6,0)$ n'est colinéaire ni à $\gamma '(2)=(0,4)$ , ni à $\gamma '(-2)=(48,-4)$ donc il y a deux points d'inflexion : $\gamma (\pm 2)$ , avec $p=1,q=3$ .

Liens externes

Gerard Eguether, « Etude de courbes paramétrées », 2012

Cet article est issu de Wikiversity. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.