Comme dans le chapitre précédent, nous n'allons pas dans ce chapitre refaire l'étude complète de la fonction dérivée. Nous supposerons que le lecteur a assimilé cette notion. Si besoin, il peut commencer par étudier la leçon « Dérivation » avant de poursuivre la lecture de ce chapitre. Nous nous contenterons ici de rappeler les principaux résultats et d'essayer de mieux comprendre tous les services que la fonction dérivée peut rendre dans l'étude d'une fonction et le tracé de sa courbe représentative.

Définition de la dérivée d'une fonction et principale propriété

Nous rappelons les définitions du nombre dérivé et de la fonction dérivée données dans les deux chapitres correspondants de la leçon « Dérivation » :

Définition

Soit ${\displaystyle f}$ une fonction. On appelle fonction dérivée de ${\displaystyle f}$, que l'on note ${\displaystyle f'}$, la fonction définie par :

${\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}$.

Le principal intérêt de la fonction dérivée est donné par le chapitre « Rapport entre dérivée et sens de variation » de la leçon « Dérivation » et résumé dans le théorème suivant :

Théorème

Soit ${\displaystyle f}$ une fonction dérivable sur un intervalle I.

• Si sa fonction dérivée ${\displaystyle f'}$ est positive (au sens large) sur I, alors la fonction ${\displaystyle f}$ est croissante sur I.
• De même, si sa fonction dérivée ${\displaystyle f'}$ est négative sur I, alors la fonction ${\displaystyle f}$ est décroissante sur I.
• Par conséquent, si ${\displaystyle f'}$ est nulle sur I, alors ${\displaystyle f}$ est constante sur I.

Nous voyons que le calcul de la fonction dérivée est une excellente méthode de déterminer des intervalles sur lesquels la fonction ƒ est croissante et d'autres sur lesquels ƒ est décroissante.

Exemple

Soit la fonction ${\displaystyle f}$ définie par :

${\displaystyle f(x)=x^{2}-2x+3}$.

Le calcul de la dérivée nous donne :

${\displaystyle f'(x)=2x-2=2(x-1)}$.

La dérivée est du même signe que ${\displaystyle x-1}$ :

• si x > 1, la dérivée est positive et l'on en déduit que la fonction est croissante sur ${\displaystyle \left[1,+\infty \right[}$.
• si x < 1, la dérivée est négative et l'on en déduit que la fonction est décroissante sur ${\displaystyle \left]-\infty ,1\right]}$.

Pour bien visualiser les variations de la courbe, on visualise les résultats dans un tableau de variation.

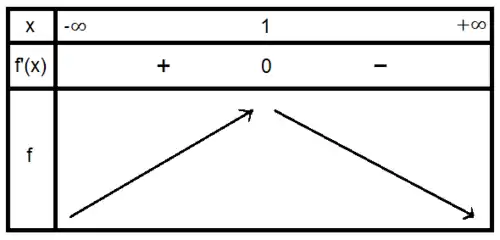
Maximum et minimum

Maximum local, minimum local

Soit f une fonction définie sur un intervalle I et soit x₀ un élément de I. On dit que f admet

• un maximum local en x₀ s'il existe un réel non nul a tel que :

  ${\displaystyle \forall x\in I\cap [x_{0}-a;x_{0}+a[\qquad f(x)\leqslant f(x_{0})}$ ;

• un minimum local en x₀ s'il existe un réel non nul a tel que :

  ${\displaystyle \forall x\in I\cap [x_{0}-a;x_{0}+a[\qquad f(x)\geqslant f(x_{0})}$.

Nous sommes donc amenés à nous poser la question suivante :

Comment, à partir de l'observation de la dérivée, peut-on en déduire que l'on a un maximum ou un minimum local ?

Théorème

Soit f une fonction numérique définie et dérivable sur un intervalle [a, b] et soit x₀ appartenant à ]a, b[.

• Si, pour tout réel x de ]a, x₀[, f'(x) est positif et pour tout réel x de ]x₀, b[, f'(x) est négatif, alors f admet un maximum (local) en x₀.
• Si, pour tout réel x de ]a, x₀[, f'(x) est négatif et pour tout réel x de ]x₀, b[, f'(x) est positif, alors f admet un minimum (local) en x₀.
• Si la fonction admet un maximum ou un minimum en x₀, alors la dérivée est nulle en x₀.

La réciproque du troisième point est fausse. En effet, il se peut que la dérivée s’annule en un point. Mais si avant et après ce point le signe de la dérivée est le même, alors la fonction n'aura pas de maximum ou de minimum en ce point. Elle marquera juste un palier. Les deux premiers points restent valables si, en x0, f est continue mais pas dérivable. Nous étudierons ce cas particulier dans un prochain chapitre. Les deux premiers points restent valables si x0 est égal à a ou b, mais pas le troisième point.

Tangente à la courbe

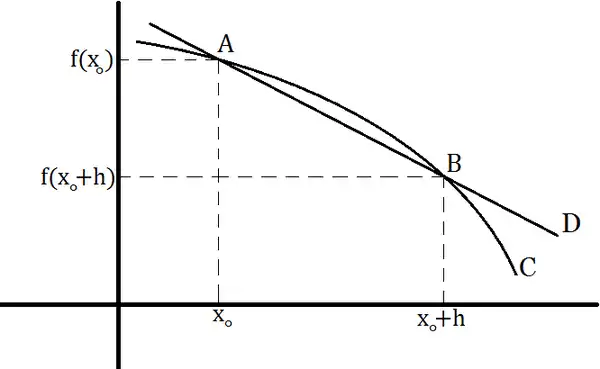
Soit C, la courbe représentative d'une fonction f. Soit A un point de la courbe C. Soit x₀, l'abscisse du point A.

Nous allons essayer de déterminer l'équation de la tangente à la courbe en A.

Soit D une droite passant par A et recoupant la courbe C en un point B d'abscisse x₀+h.

Intuitivement nous admettrons que la tangente à la courbe en A est la droite limite obtenue en rapprochant indéfiniment le point B de A, ce qui revient à faire tendre h vers 0.

Pour calculer l'équation de la tangente à la courbe en A, nous commencerons donc par établir l'équation de la droite (AB) et ensuite nous ferons tendre h vers 0.

Soit y = ax + b l'équation de la droite passant par A et B. Pour déterminer a et b, nous écrirons que la relation y = ax + b est vérifiée par les coordonnées des points A et B, on obtient :

${\displaystyle {\begin{cases}f(x_{0}+h)=a(x_{0}+h)+b\\f(x_{0})=ax_{0}+b\end{cases}}}$

Par soustraction membre à membre, nous en déduisons a :

${\displaystyle {\begin{cases}a={\frac {f(x_{0}+h)-f(x_{0})}{h}}\\f(x_{0})=ax_{0}+b\end{cases}}}$

Et en reportant a dans la deuxième équation, on obtient finalement :

${\displaystyle {\begin{cases}a={\frac {f(x_{0}+h)-f(x_{0})}{h}}\\b=f(x_{0})-{\frac {f(x_{0}+h)-f(x_{0})}{h}}x_{0}\end{cases}}}$

En reportant les valeurs de a et b dans l'équation y = ax + b, nous obtenons :

${\displaystyle y={\frac {f(x_{0}+h)-f(x_{0})}{h}}(x-x_{0})+f(x_{0})}$.

L'équation de la tangente est obtenue en faisant tendre h vers 0. L'équation de la tangente en A est donc :

${\displaystyle y=\lim _{h\to 0}{\frac {f(x_{0}+h)-f(x_{0})}{h}}(x-x_{0})+f(x_{0})}$

Mais en facteur de (x - x₀), nous reconnaissons l'expression de la dérivée en x₀. Si la fonction est dérivable en x₀, l'équation de la tangente en A peut donc s'écrire :

${\displaystyle y=f'(x_{0})(x-x_{0})+f(x_{0})}$

Nous retiendrons :

Théorème

Soit A un point d'abscisse x₀, appartenant à la courbe représentative d'une fonction f.

Si f est dérivable en x₀, alors la courbe représentative de la fonction f admet en A une tangente d'équation :

${\displaystyle y=f'(x_{0})(x-x_{0})+f(x_{0})}$.

Point d'inflexion

Un point d'inflexion.

Nous allons dire deux mots des points d'inflexion.

Définition

On appelle point d'inflexion un point où la courbe traverse sa tangente.

On définit la dérivée seconde d'une fonction f comme étant la dérivée de sa dérivée f'.

On a alors le théorème suivant permettant de trouver les abscisses des points d'inflexion :

Théorème

Un point de la courbe représentative d'une fonction f est un point d'inflexion si et seulement si la dérivée seconde f" de la fonction f s'annule en changeant de signe en l'abscisse du point considéré.

Nous admettrons ce théorème qui n'est pas toujours au programme à ce niveau.