Méthode du vecteur spatial
La méthode du vecteur spatial (Space vector modulation en anglais) est un algorithme utilisé pour réaliser la Modulation de largeur d'impulsion (MLI). Elle sert dans les onduleurs à produire la tension alternative sinusoïdale à partir d'une tension continue. Elle est principalement utilisée pour les machines électriques tournantes. L'un des objectifs de la méthode est d'obtenir un bon compromis entre la réduction le contenu harmonique[Quoi ?] de la tension produite et la réduction des pertes par commutations. Elle est intimement liée à la transformation de Clarke.
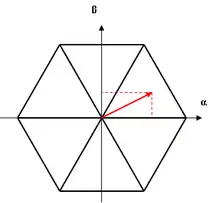
Principe
Hypothèses
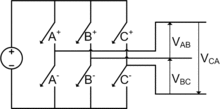
Un onduleur triphasé comme représenté ci-contre permet de créer une tension alternative triphasée, par exemple pour alimenter un moteur électrique, à partir d'une tension continue.
À aucun moment, il ne faut que deux interrupteurs en série (par exemple A- et A+) soient fermés simultanément sous peine de court-circuit. En supposant qu'au moins un des interrupteur en série est toujours fermé, on obtient huit états possibles. On note par un « 1 » l'état quand l'interrupteur du haut est fermé et par un « 0 » l'état lorsque celui du bas est fermé[1]:
| Vecteur | A+ | B+ | C+ | A− | B− | C− | VAB | VBC | VCA | |
|---|---|---|---|---|---|---|---|---|---|---|
| V0 = {000} | OFF | OFF | OFF | ON | ON | ON | 0 | 0 | 0 | vecteur de roue libre |
| V1 = {100} | ON | OFF | OFF | OFF | ON | ON | +Vdc | 0 | −Vdc | vecteur actif |
| V2 = {110} | ON | ON | OFF | OFF | OFF | ON | 0 | +Vdc | −Vdc | vecteur actif |
| V3 = {010} | OFF | ON | OFF | ON | OFF | ON | −Vdc | +Vdc | 0 | vecteur actif |
| V4 = {011} | OFF | ON | ON | ON | OFF | OFF | −Vdc | 0 | +Vdc | vecteur actif |
| V5 = {001} | OFF | OFF | ON | ON | ON | OFF | 0 | −Vdc | +Vdc | vecteur actif |
| V6 = {101} | ON | OFF | ON | OFF | ON | OFF | +Vdc | −Vdc | 0 | vecteur actif |
| V7 = {111} | ON | ON | ON | OFF | OFF | OFF | 0 | 0 | 0 | vecteur de roue libre |
On note qu'en parcourant périodiquement les états de V1 à V6, les trois phases obtenues sont distantes d'un angle de 120°, comme dans un système triphasé[1]. Toutefois, cette simple succession d'états ne permet pas d'avoir une forme d'onde sinusoïdale satisfaisante.
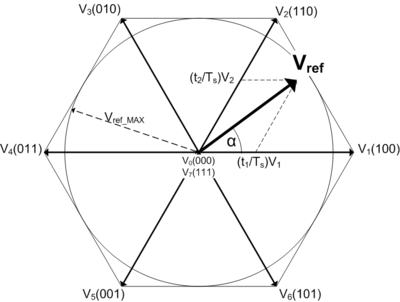
Réglage de l'angle
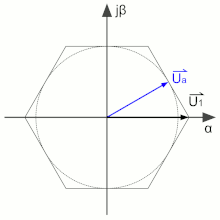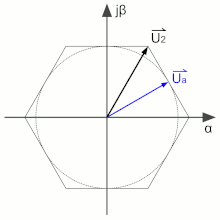
La tension alternative produite par l'onduleur permet d'alimenter une machine tournante et d'en déterminer le flux.
La modulation de largeur d'onde permet de produire un vecteur quelconque Ua (voir ci-contre) en appliquant alternativement les tensions proches (ici U1 et U2). Les enroulements du stator de la machine tournante étant fortement inductifs, le courant est lissé. La machine se comporte donc comme si elle recevait réellement la tension Ua[1].
La logique de l'algorithme commence par déterminer dans lequel des six secteurs la tension souhaitée se trouve afin de sélectionner les deux tensions à utiliser. La durée d'application de chacune des tensions permet de régler précisément l'angle de la tension résultante[1].
Afin d'avoir une tension sinusoïdale de fréquence f, la tension souhaitée tourne dans le repère à la même fréquence.
Réglage de l'amplitude
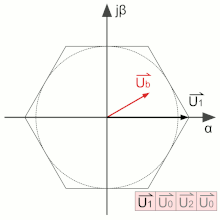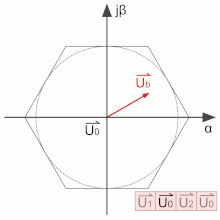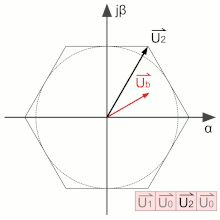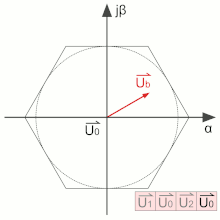
En utilisant uniquement les états allant de U1 à U6, on obtient une tension résultante maximale. Afin de réduire l'amplitude, ce qui est souhaitable pour la commande d'une machine tournante, des passages par les vecteurs de roue libre, U0 ou U7, sont insérés dans la suite des commutations. Dans l'exemple ci-contre, le temps passé dans l'état U1 relativement à celui passé dans l'état U2 est constant quelle que soit l'amplitude. Ce rapport réglant l'angle. Le passage plus ou moins long par le vecteur de roue libre permet de réduire l'amplitude. Une période de commutation alterne donc trois états : deux vecteurs actifs et un vecteur de roue libre[1].
Optimisation et surmodulation
Afin d'améliorer la forme de la tension résultante, il est possible d'appliquer le vecteur de roue libre deux fois au lieu d'une durant une période, avant et après chaque passage par un vecteur actif. La durée totale de son application restant la même.
Afin d'avoir une tension de forme sinusoïdale, la tension résultante doit rester dans le cercle de rayon dessiné. Toutefois, de manière transitoire, il est possible d'en sortir, en allant dans les coins, afin de produire un moment important dans le moteur. On parle de surmodulation. La tension n'est donc plus sinusoïdale, elle présente un contenu harmonique important qui entraîne des pertes plus élevées.
La SVM Optimisée
Plus récemment, la SVM optimisée a fait son apparition dont le principe est de ne plus considérer les secteurs de la SVM comme étant de taille égale et constant mais comme étant variables. Des méthodes d'optimisation sont alors employées afin de choisir la taille des secteurs. L'optimisation est classiquement faite de manière à minimiser le WTHD, qui a pour avantage de ne pas dépendre de la charge considérée.
Lien avec les MLI intersectives
Il est possible de démontrer que la SVM classique peut se ramener à une MLI intersective par injection d'harmoniques dans la modulante (ou ajout d'une tension de mode commun) à la tension de référence. la tension de mode commun à ajouter est alors égale à : .
Avec Vref, le vecteur de tension de référence noté: .
Ainsi la modulante à comparer avec la porteuse triangulaire devient:
.
Les notations utilisées sont les suivantes:
- Tension de Bus.
- Tension de mode commun.
- indice de modulation.
- pulsation de référence.
Tension de consigne
La méthode a besoin d'une tension de référence échantillonnée à une fréquence fs (Ts = 1/fs). L'utilisation de la transformée de Clarke permet d'obtenir une tension de référence unique à partir d'un système triphasé.
Vecteur spatial 3D
Une méthode du vecteur spatial en 3D existe également. Elle permet de commander les onduleurs à quatre branches. Le vecteur n'est plus représenté dans un hexagone mais dans un prisme en trois dimensions, comme un prisme hexagonal si on utilise la transformée de Clarke[2] ou un dodécaèdre sinon[3].
Applications
La méthode est utilisée pour commander les onduleurs connectés à des machines électriques asynchrones, synchrones ou à courant continu sans balais. Elle est souvent utilisée en combinaison avec une commande vectorielle pour produire la consigne de tension.
Notes et références
- (de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Raumzeigermodulation » (voir la liste des auteurs).
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Space vector modulation » (voir la liste des auteurs).
- « Les Différents Stratégies de Modulation » (consulté le )
- (en) R. Zhang, V. Himamshu Prasad, D. Boroyevich et F.C. Lee, « Three-Dimensional Space Vector Modulation for Four-Leg Voltage-Source Converters », IEEE Power Electronics Letters, vol. 17, no 3,
- (en) M.A. Perales, M.M. Prats, R. Portillo, J.L. Mora, J.I. León et L.G. Franquelo, « Three-Dimensional Space Vector Modulation in abc Coordinates for Four-Leg Voltage Source Converters », IEEE Power Electronics Letters, vol. 1, no 4,
Bibliographie
- (de) Dierk Schröder, Elektrische Antriebe : Grundlagen, Berlin, Heidelberg, Springer, (ISBN 978-3-642-02989-9)
- (de) Dierk Schröder, Antriebe : Regelung von Antriebssystemen, Berlin, Heidelberg, Springer, , 1336 p. (ISBN 978-3-540-89612-8)
- Portail de l’électricité et de l’électronique