Transformée de Clarke

La transformée de Clarke, est un outil mathématique utilisé en électrotechnique, et en particulier pour la commande vectorielle, afin de modéliser un système triphasé grâce à un modèle diphasé. Il s'agit d'un changement de repère. Les deux premiers axes dans la nouvelle base sont traditionnellement nommés α, β. Les grandeurs transformées sont généralement des courants, des tensions ou des flux.

La transformée de Clarke modélise une machine tournante à trois enroulements alimentés par des courants triphasés par deux enroulements perpendiculaires fixes, alimentés par des courants sinusoïdaux

Dans le cas d'une machine synchrone, le repère de Clarke est fixé au stator.

La transformée de Concordia est très similaire à la transformée de Clarke, à la différence qu'elle est unitaire. Les puissances calculées après transformation sont donc les mêmes que dans le système initial, ce qui n'est pas le cas pour la transformée de Clarke.

Transformée de Clarke

Matrices de Clarke

Edith Clarke a proposé la transformation en 1951[1]. Soit a, b et c le repère initial d'un système triphasé. α, β et o est le repère d'arrivée. La matrice de Clarke vaut :

i_{\alpha \beta o}(t)=Pi_{abc}(t)={\frac {2}{3}}{\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\\\end{bmatrix}}{\begin{bmatrix}i_{a}(t)\\i_{b}(t)\\i_{c}(t)\end{bmatrix}}

La matrice inverse est :

i_{abc}(t)=P^{-1}i_{\alpha \beta o}(t)={\begin{bmatrix}1&0&1\\-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}&1\\-{\frac {1}{2}}&-{\frac {\sqrt {3}}{2}}&1\end{bmatrix}}{\begin{bmatrix}i_{\alpha }(t)\\i_{\beta }(t)\\i_{o}(t)\end{bmatrix}}

L’axe $0_{\beta }$ est indirect par rapport à l’axe $0_{\alpha }$ .

Intérêt

Considérons un système de trois courants triphasés équilibrés:

{\begin{aligned}i_{a}(t)=&{\sqrt {2}}I\cos(\theta (t)),\\i_{b}(t)=&{\sqrt {2}}I\cos \left(\theta (t)-{\frac {2}{3}}\pi \right),\\i_{c}(t)=&{\sqrt {2}}I\cos \left(\theta (t)+{\frac {2}{3}}\pi \right).\end{aligned}}

Où $I$ est la valeur effective du courant et $\theta (t)$ l'angle. On pourrait tout aussi bien remplacer $\theta (t)$ par $\omega t$ sans perte de généralité. En appliquant la transformation de Clarke, on obtient :

{\begin{aligned}i_{\alpha }=&{\sqrt {2}}I\cos \theta (t),\\i_{\beta }=&{\sqrt {2}}I\sin \theta (t),\\i_{o}=&0.\end{aligned}}

$i_{o}$ est nul dans le cas d'un système triphasé équilibré. Les problèmes de dimension trois se réduisent donc à des problèmes de dimension deux. L'amplitude des courants $i_{\alpha }$ et $i_{\beta }$ est la même que celles des courants $i_{a}$ , $i_{b}$ et $i_{c}$ .

Forme simplifiée

$i_{o}$ étant nul dans le cas d'un système triphasé équilibré, une forme simplifiée de la transformée dans ce cas est [2]:

i_{\alpha \beta }(t)={\frac {2}{3}}{\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\end{bmatrix}}{\begin{bmatrix}i_{a}(t)\\i_{b}(t)\\i_{c}(t)\end{bmatrix}}

La matrice inverse vaut alors :

i_{abc}(t)={\frac {3}{2}}{\begin{bmatrix}{\frac {2}{3}}&0\\-{\frac {1}{3}}&{\frac {\sqrt {3}}{3}}\\-{\frac {1}{3}}&-{\frac {\sqrt {3}}{3}}\end{bmatrix}}{\begin{bmatrix}i_{\alpha }(t)\\i_{\beta }(t)\end{bmatrix}}

Électrotechnique

Une composante homopolaire $x_{0}$ est rajoutée afin de prendre en compte un système déséquilibré. La composante homopolaire est la somme des trois grandeurs divisée par trois dans la théorie des composants symétriques $x_{0}={\frac {1}{3}}(x_{a}+x_{b}+x_{c})$ .

${\begin{bmatrix}x_{a}\\x_{b}\\x_{c}\end{bmatrix}}={\begin{bmatrix}1&0&1\\-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}&1\\-{\frac {1}{2}}&-{\frac {\sqrt {3}}{2}}&1\end{bmatrix}}{\begin{bmatrix}x_{\alpha }\\x_{\beta }\\x_{0}\end{bmatrix}}$

Associée à la transformée de Park, permettant de représenter le système triphasé dans un repère tournant, la transformation Park-Clark devient :

${\begin{bmatrix}x_{d}\\x_{q}\end{bmatrix}}={\frac {2}{3}}{\begin{bmatrix}cos(\theta )&cos(\theta -{\frac {2.\pi }{3}})&cos(\theta -{\frac {4.\pi }{3}})\\-sin(\theta )&-sin(\theta -{\frac {2.\pi }{3}})&-sin(\theta -{\frac {4.\pi }{3}})\end{bmatrix}}{\begin{bmatrix}x_{a}\\x_{b}\\x_{c}\end{bmatrix}}$

Noter que la transformée de Park-Clark assure la conservation des amplitudes des grandeurs, mais pas des puissances électriques, à la différence de la transformée de Park-Concordia.

Noter également que l'amplitude d'un vecteur dans le repère de Park ne dépend pas de l'angle $\theta$ , et peut être obtenu par la formule suivante :

${\begin{vmatrix}x_{d}\\x_{q}\end{vmatrix}}=x_{a}^{2}+x_{b}^{2}+x_{c}^{2}-x_{a}.x_{b}-x_{a}.x_{c}-x_{b}.x_{c}$

Interprétation géométrique

Géométriquement la transformation de Clarke est une combinaison de rotations. En partant d'un espace en trois dimensions ayant pour axes orthogonaux a, b, et c.

Une rotation d'axe a d'angle -45° est effectuée. La matrice de rotation est :

{\begin{bmatrix}1&0&0\\0&\cos(-\pi /4)&\sin(-\pi /4)\\0&-\sin(-\pi /4)&\cos(-\pi /4)\end{bmatrix}}

Soit

{\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&{\frac {-1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}

On obtient donc le nouveau repère suivant :

Une rotation d'axe b' et d'angle environ 35.26° ( $\phi =\cos ^{-1}{\sqrt {\frac {2}{3}}}$ ) est ensuite effectué :

{\begin{bmatrix}\cos(\phi )&0&-\sin(\phi )\\0&1&0\\\sin(\phi )&0&\cos(\phi )\end{bmatrix}}

Soit

{\begin{bmatrix}{\frac {\sqrt {2}}{\sqrt {3}}}&0&{\frac {-1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\frac {\sqrt {2}}{\sqrt {3}}}\end{bmatrix}}

La composition de ces deux rotations a pour matrice :

{\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}={\begin{bmatrix}{\frac {\sqrt {2}}{\sqrt {3}}}&0&{\frac {-1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\frac {\sqrt {2}}{\sqrt {3}}}\end{bmatrix}}\cdot {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&{\frac {-1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}

Cette matrice est appelée matrice de Clarke.

Les axes sont renommés α, β et z. L'axe z est à 'égales distances' des trois axes initiaux a, b, et c (il passe par le centre du triangle (a,b,c)). Si le système initial est équilibré, la composante en z est donc nulle, et le système est simplifié.

Transformée de Concordia

A la différence de la transformée de Clarke qui n'est pas unitaire, la transformée de Concordia conserve la puissance. Les puissances actives et réactives calculées dans le nouveau système ont donc les mêmes valeurs que dans le système initial. La matrice de Concordia vaut :

i_{\alpha \beta o}(t)=Pi_{abc}(t)={\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}}{\begin{bmatrix}i_{a}(t)\\i_{b}(t)\\i_{c}(t)\end{bmatrix}}

La matrice inverse de Concordia est égale à la transposée de la matrice Concordia[3] :

i_{abc}(t)=P^{-1}i_{\alpha \beta o}(t)={\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&0&{\frac {\sqrt {2}}{2}}\\-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}&{\frac {\sqrt {2}}{2}}\\-{\frac {1}{2}}&-{\frac {\sqrt {3}}{2}}&{\frac {\sqrt {2}}{2}}\\\end{bmatrix}}{\begin{bmatrix}i_{\alpha }(t)\\i_{\beta }(t)\\i_{o}(t)\end{bmatrix}}

Si les puissances sont conservées, les amplitudes des grandeurs initiales ne le sont pas. Dans le détail :

{\begin{aligned}i_{\alpha }=&{\sqrt {3}}I\cos \theta (t),\\i_{\beta }=&{\sqrt {3}}I\sin \theta (t),\\i_{o}=&0.\end{aligned}}

Transformation de Park

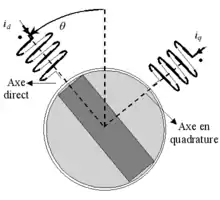
La transformée de Park modélise une machine tournante à trois enroulements alimentés par des courants triphasés par deux enroulements perpendiculaires tournant avec le rotor, alimentés par des courants continus

La transformée de Park reprend les principes de la transformée de Clarke, mais la pousse plus loin. Après la transformée de Clarke d'un système triphasé équilibré, on obtient le système suivant :

{\begin{aligned}i_{\alpha }=&{\sqrt {2}}I\cos \theta (t),\\i_{\beta }=&{\sqrt {2}}I\sin \theta (t),\\i_{o}=&0.\end{aligned}}

La transformée de Park vise à supprimer le caractère oscillatoire de $i_{\alpha }$ et $i_{\beta }$ en effectuant une rotation supplémentaire d'angle $\theta$ par rapport à l'axe o.

L'idée est de faire tourner le repère à la vitesse du rotor de la machine tournante. Le repère de Clarke est fixé au stator, tandis que celui de Park est fixé au rotor. Cela permet de simplifier certaines équations électromagnétiques.

Voir aussi

Liens internes

Liens externes

Transformation des systèmes triphasés Fortescue, Clarke, Park et Ku

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Alpha–beta transformation » (voir la liste des auteurs).

(en) W. C. Duesterhoeft, Max W. Schulz et Edith Clarke, « Determination of Instantaneous Currents and Voltages by Means of Alpha, Beta, and Zero Components », Transactions of the American Institute of Electrical Engineers, vol. 70, n^o 2,‎ juillet 1951, p. 1248–1255 (ISSN 0096-3860, DOI 10.1109/T-AIEE.1951.5060554)
(en) F. Tahri, A. Tahri, Eid A. AlRadadi et A. Draou Senior, Analysis and Control of Advanced Static VAR compensator Based on the Theory of the Instantaneous Reactive Power, Bodrum, ACEMP, 2007
(en) S. Chattopadhyay, M. Mitra et S. Sengupta, « Area Based Approach for Three Phase Power Quality Assessment in Clarke Plane », Journal of Electrical Systems, vol. 04, n^o 01,‎ 2008, p. 62 (lire en ligne, consulté le 2 mai 2015)

Portail de l’électricité et de l’électronique
Portail de l’énergie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) W. C. Duesterhoeft, Max W. Schulz et Edith Clarke, « Determination of Instantaneous Currents and Voltages by Means of Alpha, Beta, and Zero Components », Transactions of the American Institute of Electrical Engineers, vol. 70, n^o 2,‎ juillet 1951, p. 1248–1255 (ISSN 0096-3860, DOI 10.1109/T-AIEE.1951.5060554)

[Tahri-2] (en) F. Tahri, A. Tahri, Eid A. AlRadadi et A. Draou Senior, Analysis and Control of Advanced Static VAR compensator Based on the Theory of the Instantaneous Reactive Power, Bodrum, ACEMP, 2007

[3] (en) S. Chattopadhyay, M. Mitra et S. Sengupta, « Area Based Approach for Three Phase Power Quality Assessment in Clarke Plane », Journal of Electrical Systems, vol. 04, n^o 01,‎ 2008, p. 62 (lire en ligne, consulté le 2 mai 2015)