Formule de Stirling
La formule de Stirling, du nom du mathématicien écossais James Stirling, donne un équivalent de la factorielle d'un entier naturel n quand n tend vers l'infini :
Pour les articles homonymes, voir Stirling.
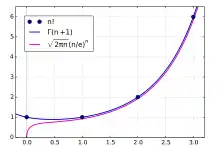
que l'on trouve souvent écrite ainsi :
où le nombre e désigne la base de l'exponentielle.
Histoire
C'est Abraham de Moivre[1] qui a initialement démontré la formule suivante :
où C est une constante réelle (non nulle).
L'apport de Stirling[2] fut d'attribuer la valeur C = √2π à la constante et de donner un développement de ln(n!) à tout ordre.
Démonstration
- La détermination de la constante n'est pas immédiate, mais il est facile de montrer le résultat de De Moivre, en vérifiant que est la n-ième somme partielle d'une série télescopique convergente[3]. La façon classique d'en déduire ensuite la formule asymptotique est exposée dans l'article sur les intégrales de Wallis.
- Pour introduire le facteur de De Moivre, une autre manière de présenter est la suivante : la formule d'Euler-Maclaurin appliquée à la fonction ln entre 1 et n donne
On prend alors l'exponentielle et cela donne l'idée du calcul ci-dessus. - On peut même introduire le facteur √2π par la méthode de la descente rapide. Cette méthode est assez puissante et en l'appliquant, on « comprend » l'apparition du √2π et l'on trouve immédiatement le résultat de Stirling.
- Mais on peut aussi démontrer directement, et de façon élémentaire, un résultat plus précis sur la fonction Γ d'Euler[4], dont le cas particulier pour la factorielle s'écrit :
- .
Développement asymptotique
En supposant le coefficient C = √2π déjà connu, la formule d'Euler-Maclaurin donne le développement asymptotique de ln(n!) au voisinage de l’infini à l’ordre K ≥ 1 :
où les Bi sont les nombres de Bernoulli. Il est à noter que la somme ci-dessus ne tend pas vers une limite finie lorsque K tend vers l’infini.
Sachant que, à part B1 (qui n’intervient pas dans la formule), tous les nombres de Bernoulli de rang impair sont nuls, on peut réécrire le développement (à l’ordre 2K) :
On définit la fonction de Binet μ en faisant tendre formellement K vers l’infini :
ce qui permet d’écrire :
En calculant les premiers termes de e μ(n) grâce à la formule exponentielle (en) (laquelle fait intervenir les polynômes de Bell), on a alors le développement asymptotique de n! au voisinage de l’infini :
développement dont les numérateurs et dénominateurs sont référencés respectivement par les suites ![]() A001163 et
A001163 et ![]() A001164 de l'OEIS.
Il s’agit également du développement asymptotique de la fonction gamma.
A001164 de l'OEIS.
Il s’agit également du développement asymptotique de la fonction gamma.
Version continue
La formule précédente est une conséquence, pour le cas particulier d'un argument entier, de la formule asymptotique de Stirling pour la fonction gamma :
Calculs numériques
Précision de la formule de Stirling
Pour juger de sa précision, on peut faire le tableau des premières valeurs de n :
| n | n ! | ||
|---|---|---|---|
| 1 | 1 | 0,92 | 0,999 |
| 2 | 2 | 1,92 | 1,999 |
| 3 | 6 | 5,84 | 5,998 |
| 4 | 24 | 23,51 | 23,996 |
| 5 | 120 | 118,02 | 119,99 |
| 6 | 720 | 710,08 | 719,94 |
| 7 | 5 040 | 4 980,4 | 5 039,7 |
| 8 | 40 320 | 39 902,4 | 40 318,1 |
| 9 | 362 880 | 359 536,9 | 362 866,0 |
| 10 | 3 628 800 | 3 598 696 | 3 628 685 |
| 15 | 1 307 674 368 000 | 1,300 431 × 1012 | 1,307 665 × 1012 |
| 20 | 2 432 902 008 176 640 000 | 2,422 787 × 1018 | 2,432 882 × 1018 |
| 25 | 15 511 210 043 330 985 984 000 000 | 1,545 959 × 1025 | 1,551 113 × 1025 |
| 30 | 265 252 859 812 191 058 636 308 480 000 000 | 2,645 171 × 1032 | 2,652 519 × 1032 |
| 40 | 815 915 283 247 897 734 345 611 269 596 115 894 272 000 000 000 | 8,142 173 × 1047 | 8,159 136 × 1047 |
Dans √n, si l'on remplace n par n + 16, les calculs sont nettement améliorés, pour les petites valeurs de n (approximation de Gosper) ; on peut aussi préférer un encadrement[5] ; enfin, on peut prendre la suite A055775 de l'OEIS.
Approximations exploitables pour des machines à calculer
L'approximation
- ,
ou de façon équivalente
- ,
peut être obtenue en réarrangeant la formule étendue de Stirling et en remarquant une coïncidence entre la série des puissances résultante et le développement en série de Taylor de la fonction sinus hyperbolique. Cette approximation est valable jusqu'à plus de 8 décimales pour z ayant une partie réelle supérieure à 8. Robert H. Windschitl l'a suggérée en 2002 pour calculer la fonction gamma avec une bonne précision sur des machines à calculer à programme ou mémoire de registre limité(e)[6].
Gergő Nemes a proposé en 2007 une approximation qui donne le même nombre de chiffres exacts que celle de Windschitl mais qui est bien plus simple[7] :
- ,
ou de façon équivalente
- .
Approximation logarithmique
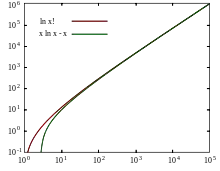
Dans le cadre de la thermodynamique statistique (distribution de Boltzmann) il est commode de considérer le logarithme népérien d'une factorielle en faisant l'approximation de Stirling[8]. L'approximation consiste à assimiler la somme à une intégrale quand n est suffisamment grand[9].
On obtient finalement l'approximation suivante :
pour laquelle l'erreur relative est inférieure à 1 % quand n > 100. Cette approximation est considérée comme valable (l'erreur est négligeable) dans le cadre de la distribution de Boltzmann étant donné les grandes valeurs de n utilisées (représentant les configurations microscopiques d'un état macroscopique).
Une approximation bien plus précise de ln(n!) a été donnée par Srinivasa Ramanujan[10] :
Notes et références
- À l'occasion de sa démonstration du théorème central limite dans le cas particulier de la loi binomiale.
- (la) Jacobo Stirling, Methodus Differentialis sive Tractatus de Summatione et Interpolatione Serierum Infinitarum (1730), proposition 28, p.135. La valeur du logarithme décimal de √2π est donnée p. 137.
- Voir par exemple .
- Voir le document .
- (en) Eric W. Weisstein, « Stirling's Approximation », sur MathWorld.
- (en) V. T. Toth, Programmable Calculators: Calculators and the Gamma Function (2006).
- (en) Gergő Nemes, « New asymptotic expansion for the Gamma function », Archiv der Mathematik, vol. 95, no 2, , p. 161-169 (ISSN 0003-889X, DOI 10.1007/s00013-010-0146-9).
- Atkins, Chimie Physique, 3e éd., deBoeck, Bruxelles, 2008.
- Jannès, Chimie Physique : Distribution de Boltzmann, HELdB IMC, Bruxelles, 2010.
- (en) M. Trott, The Mathematica GuideBook for Symbolics, Birkhäuser, , 1454 p. (ISBN 978-0-387-95020-4, lire en ligne), p. 359.
- Portail de l'analyse