Modèle ellipsoïdal de la Terre
La Terre fut longtemps considérée comme étant sphérique, tout d'abord par Parménide (v. 515-450 av. J.-C.) essentiellement pour des raisons esthétiques et géométriques, puis par Platon (v. 428-348 av. J.-C.) pour qui la forme des éclipses de Lune montre que l'ombre projetée de la Terre est toujours circulaire. Cette idée de Terre sphérique sera peu à peu remplacée par l'idée que la Terre présente une forme ellipsoïdale.
Premières idées que la Terre n'est pas sphérique, mais ellipsoïdale

Les premières indications que la Terre dans son ensemble est légèrement ellipsoïdale, sont à la fois de nature empirique et de nature théorique. Ainsi, Jean-Dominique Cassini avait observé dès 1666 que Jupiter était fortement aplatie. Cette découverte avait aussi été faite en Angleterre par John Flamsteed. L'aplatissement en cause vaut environ 1/15. Il était tentant de mettre ce fait en rapport avec la rotation rapide de Jupiter sur lui-même en un peu moins de 10 heures. Il en allait de même pour Saturne. Par analogie, il était naturel de penser que la Terre elle-même fût quelque peu aplatie.
D'autre part, l'observation de Jean Richer montrant que la longueur du pendule qui battait la seconde était plus grande à Paris qu'à Cayenne fut connue de Newton et de Huyghens, et suscita leur réflexion. Huyghens en déduisit dans son « Discours sur la cause de la pesanteur », paru en 1690, que la Terre est un corps de révolution aplati et, compte tenu de la force centrifuge dont il avait fait lui-même la théorie, il trouve[1],[2] un aplatissement de 1/578.
En 1687, Newton considère dans les « Principia mathematica philosophiae naturalis » une Terre fluide dont la masse volumique est constante du centre à la surface[3], valant environ 5,5 fois celle de l'eau, tournant sur elle-même en 24 heures. S'appuyant sur sa théorie de la gravitation universelle, il trouve que dans ces circonstances, l'aplatissement des surfaces de niveau internes est lui-même constant du centre à la surface et vaut 1/230, à peu de chose près.
Le résultat de Richer s'interprète en notant que sur l'ellipsoïde, la pesanteur g n'est pas constante : pour un ellipsoïde aplati aux pôles, où un point de la surface situé à une latitude plus élevée se trouve plus près du centre de masse qu'un tel point situé à une latitude moins élevée, elle est plus grande aux pôles qu'à l'équateur. Sachant que la période propre d'un pendule simple vaut 2π (ℓ/g)1/2, où ℓ est la longueur du pendule, et que g possède une valeur supérieure à Paris qu'à Cayenne, on comprend que Richer ait dû raccourcir la longueur de son pendule près de l'équateur pour qu'il batte au même rythme qu'à Paris.
Il convient de noter que l'idée d'une Terre aplatie était en rupture complète avec les idées philosophiques traditionnelles héritées des Anciens. En effet, selon les auteurs comme Pythagore, Platon, Aristote, Ptolémée et leur disciples, la Terre devait nécessairement être une sphère, puisque la Terre érigée en divinité cosmique devait être parfaite, et que la sphère est le corps solide «parfait» par excellence. C'est sans aucun doute l'œuvre de Kepler, qui avait osé remplacer les orbites planétaires circulaires par des ellipses, qui fut à l'origine de l'évolution des idées conduisant finalement à ce changement radical des conceptions philosophiques[4].
Les « Principia » connaîtront plusieurs éditions au cours des décennies suivantes et exerceront une très grande influence sur la Science et la Philosophie. Au fur et à mesure de la parution de ces nouvelles éditions, l'ouvrage fut complété et mis à jour.
En 1683, donc un peu avant la parution de la première édition des « Principia », la méridienne de Picard entre Sourdon et Malvoisine commençait à être prolongée sous la direction de Jean-Dominique Cassini, vers le nord par La Hire, disciple de Picard, et vers le sud par Cassini lui-même. La méridienne de Cassini a joué un rôle historique suffisamment important pour qu'il soit utile de fournir quelques détails à son sujet[5]. Les travaux furent interrompus dès la fin de l'année à cause de la mort de Colbert et son remplacement comme protecteur de l'Académie et surintendant des bâtiments du Roi par Louvois. Ce dernier avait d'autres priorités. La Hire était parvenu à Béthune, et Cassini à Bourges.
La méridienne de Cassini
Louvois mourut en 1691, mais les travaux ne reprenaient qu'en 1700, toujours sous la direction de Jean-Dominique Cassini. Ce dernier s'adjoignit son fils Jacques (1677-1756). Les travaux poursuivis jusqu'au pic du Canigou dans les Pyrénées orientales, non loin de Perpignan, se terminèrent en 1701 par la mesure de la base de Leucate-Saint Nazary. Autant dire qu'on avait fait vite : lever en un an et demi la méridienne Bourges–Canigou, avec les moyens de transport et de communication de l'époque, apparaît encore maintenant comme une gageure. La raison de cette rapidité d'exécution fut sans doute la guerre de Succession d'Espagne, qui absorbait pratiquement tous les crédits, et qui laissait la partie nord de la méridienne inachevée. Ce n'est qu'après une longue interruption que les travaux purent être repris en 1718 par Jacques Cassini, Maraldi et La Hire fils. La méridienne put ainsi être achevée entre Sourdon et Montdidier, puis prolongée jusqu'à Dunkerque où l'on mesura une base. La chaîne complète de la méridienne de Cassini est appuyée sur trois bases. Du nord au sud, on trouve la base de Dunkerque (5564 toises, soit environ 10 844 mètres), la base mesurée par Picard à Villejuif (5663 toises, ou 11 037 mètres), et la base de Leucate (7246 toises, ou 14 122 mètres). Les stations astronomiques fondamentales en sont l'Observatoire de Paris, à une latitude de +48°50′10″, Dunkerque à 2°12′15,5″ au nord de Paris (donc à une latitude de +51°02′25,5″), et Collioure à 6°18′56″ au sud de Paris (donc à une latitude de +42°31′14″).
Les travaux de cette méridienne historique sont résumés dans un livre de Jacques Cassini paru en 1723, le « Traité de la grandeur et de la Figure de la Terre ». L'auteur y fournit les valeurs numériques citées ci-dessus, et y annonce 57097 toises pour le degré de méridien du segment sud (Paris–Collioure), et 56960 toises pour le segment nord (Paris–Dunkerque). Rappelons que Picard avait trouvé 57060 toises pour le segment central Paris–Amiens.
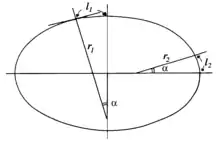
Jacques Cassini annonce 57061 toises pour le degré de méridien de la sphère moyenne, et il ramène le degré de Picard à 57030 toises. Il conclut «… ainsi, il paraît avec assez d'évidence que les degrés d'un méridien sont plus grands plus ils sont près de l'équateur et diminuent au contraire à mesure qu'ils s'approchent du pôle ». Cela signifiait que la forme de la Terre était un ellipsoïde allongé aux pôles. En effet, la sphère tangente au pôle possède un plus grand rayon (r = r1) que la sphère tangente à l'équateur (r = r2). Par conséquent, un angle α sous-tend un arc de méridien ℓ = α r plus grand au pôle qu'à l'équateur : ℓ1 > ℓ2. Pour un ellipsoïde aplati aux pôles, c'est l'inverse qui a lieu, c'est–à-dire ℓ1 < ℓ2. En extrapolant la méridienne de Cassini vers le pôle nord et vers l'équateur, on trouve ℓ1 < ℓ2.
Étant en contradiction avec les travaux théoriques de Huyghens et de Newton, qui démontraient au contraire que la Terre, du fait de sa rotation, devait être un ellipsoïde aplati aux pôles, et non pas allongé, cette thèse de Cassini fut le point de départ d'une controverse scientifique, à laquelle se mêlait la politique, qui allait durer quinze ans. Le débat fut finalement tranché en 1737 par l'expérience en faveur d'un sphéroïde, c'est-à-dire d'un ellipsoïde de révolution aplati aux pôles. La moisson scientifique de ce débat ne peut guère être exagérée, car le problème de la figure de la Terre donna lieu à de nombreux progrès en géodésie astronomique bien sûr, mais aussi en hydrostatique, en physique et en mathématiques. La plupart des fonctions dites « spéciales » de la physique mathématique et théorique, inventées au cours des XVIIIe et XIXe siècles, prennent leur origine dans des travaux consacrés à la forme de la Terre. Le problème reste toujours actuel, mais à un niveau de complexité plus élevé.
En fait, si l'on examine la méridienne de Cassini hors de tout contexte polémique, on se rend compte que la configuration de la chaîne laisse fort à désirer. Cela est surtout vrai dans sa partie sud, où la conformation des triangles est fort médiocre.
Les conceptions de Newton ont été vite acceptées par les savants britanniques, mais sur le continent — et particulièrement en France — les opinions restaient partagées. La vieille théorie des tourbillons due à Descartes, revue et corrigée par Huyghens, emportait encore de nombreux suffrages, et la liaison entre attraction gravitationnelle et pesanteur n'était pas perçue clairement. D'autre part, Jacques Cassini continuait, non sans aigreur, à défendre ses mesures, et donc l'idée d'une Terre allongée aux pôles. On assistait ainsi à ce qu'on a appelé la «querelle entre les têtes pointues (les Cassiniens) et les têtes plates (les Newtoniens)». Voltaire se rangeait parmi les philosophes célèbres qui s'étaient ralliés aux thèses de Newton. Parmi les savants français acquis à celles-ci figurait notamment Maupertuis. C'est à ce dernier qu'allait échoir l'honneur de démontrer empiriquement, lors d'une expédition en Laponie, que la Terre était bien aplatie aux pôles.
Notes et références
- Si l'on désigne par ω la vitesse angulaire de la rotation terrestre et par m le rapport ω²R/g de l'accélération centrifuge équatoriale ω²R à l'accélération de la pesanteur g, la mesure astronomique de ω combinée avec le résultat obtenu par Picard pour la valeur du rayon terrestre R fournit approximativement m = 1/289. Huyghens considère une Terre sphérique en rotation à la vitesse ω et se demande quelle forme adopterait un fluide superficiel soumis à la fois à l'attraction centrale de la Terre et à l'accélération centrifuge. En composant les deux vecteurs, il montre que leur résultante est normale à un sphéroïde d'aplatissement f valant ½m. On a donc : f = 1/576. En réalité, la Terre étant un corps déformable, toutes les couches internes sont elles-mêmes aplaties et l'attraction n'est pas centrale. Pour que l'attraction sur la couche fluide superficielle fût centrale, il faudrait que toute la masse fût concentrée au centre et que l'enveloppe possédât une masse négligeable. Un tel modèle représente le cas-limite d'une distribution de masse volumique infiniment concentrée et fournit une limite inférieure pour l'aplatissement terrestre en surface.
- Œuvres complètes de Huygens, tome XXI, p.383
- Il est évident que la Terre réelle ne peut pas posséder une masse volumique constante du centre à la surface, mais que celle-ci doit être plus petite à la surface qu'au centre, notamment à cause de la pression qui croît avec la profondeur. La formule établie par Newton pour l'aplatissement d'un fluide homogène, à savoir f = (5/4)m [qui donne : f = (5/4)x(1/288) = 1/230,4], fournit une borne supérieure pour l'aplatissement réel. Ce dernier vaut 1/298,3 ; il se situe donc effectivement entre la borne inférieure de Huyghens (1/578) et la borne supérieure de Newton (1/230).
- Selon K.E. Bullen The Earth's Density, Chapman and Hall, London, 1975, p. 7), la plus ancienne suggestion connue que la forme de la Terre est aplatie est fournie par Strabon, dans un ouvrage paru quelques années avant notre ère. Strabon y fait référence à une supposition de Polybius (env. 203–120 av. J.-C.) que les régions équatoriales de la Terre seraient élevées. Il s'agit sans doute ici d'une hypothèse sans fondement scientifique. Elle ne fut guère retenue au cours des siècles suivants et n'a joué aucun rôle dans l'émergence du modèle de Terre aplatie, tel qu'il est envisagé ici. Celui-ci repose sur de solides bases observationnelles et mécaniques.
- Pour de nombreux autres détails sur l'histoire de la géodésie en France depuis trois siècles, le lecteur intéressé pourra se rapporter au magnifique ouvrage de Jean-Jacques Levallois Mesurer la Terre (300 ans de géodésie française — De la toise du Châtelet au satellite), Association française de topographie – Presses de l'École nationale des Ponts et Chaussées, 1988.
Voir aussi
Bibliographie
- Dugas, R. (1950). Histoire de la Mécanique, Éditions du Griffon, Neuchâtel & Éditions Dunod, Paris.
- Lacombe, H. & P. Costabel, éditeurs (1988). La figure de la Terre du XVIIIe siècle à l'ère spatiale, Académie des Sciences et Gauthier-Villars, Paris.
- Levallois, J.-J. (1988). Mesurer la Terre (300 ans de géodésie française — De la toise du Châtelet au satellite), Association française de topographie — Presses de l'École nationale des Ponts et Chaussées.
- Taton, R. (1994). Histoire générale des sciences (4 volumes), Quadrige/Presses universitaires de France.
Articles connexes
Voici quelques liens vers des articles ayant trait à l'histoire de la géodésie et de la Figure de la Terre :
- Figure de la Terre dans l'Antiquité
- Figure de la Terre au Moyen Âge
- Figure de la Terre à la Renaissance
- Figure de la Terre et gravitation universelle
- Expéditions géodésiques françaises
- Figure de la Terre et méridienne de Delambre et Méchain
- Figure de la Terre et histoire du mètre
- Masse de la Terre
- Sphéroïde de Clairaut
Liens externes
- Champs géophysiques, pour une description du géoïde par décomposition en harmoniques sphériques
- Portail de la géodésie et de la géophysique
- Portail de l’astronomie
- Portail de la physique
- Portail de la géographie