Convection thermique

La convection (thermique) désigne le transfert d'énergie thermique au sein d'un fluide en mouvement ou entre un fluide en mouvement et une paroi solide. Ce transfert d'énergie est réalisé par deux modes de transfert élémentaire combinés que sont l'advection et la diffusion.

La convection constitue, avec la conduction et le rayonnement, l'un des trois modes d'échange de chaleur entre deux systèmes, et diffère de ces derniers par la méthode de transfert.

Convection forcée

On parle de convection forcée lorsque l'écoulement du fluide est provoquée par un organe « artificiel » (pompe, turbine, ventilateur...).

Voici quelques exemples de convection forcée dans des appareillages : chauffage central avec accélérateur, chauffages électriques avec soufflerie, chauffe-eau solaire et four à convection (four à chaleur tournante). Le corps humain a son propre système de convection forcée, la circulation sanguine.

Convection naturelle

Convection naturelle.

La convection naturelle est un phénomène de la mécanique des fluides, qui se produit lorsqu'un gradient induit un mouvement dans le fluide. Le gradient peut concerner différentes grandeurs intensives telles que la température (« convection thermique »), la concentration d'un soluté (« convection solutale ») ou la tension superficielle (« convection thermo-capillaire »). La masse volumique dépendant de la température (et, le cas échéant, de la concentration), un gradient de température ou de concentration engendre des différences de masse volumique au sein du fluide, d'où résultent des variations latérales de la poussée d'Archimède qui sont à l'origine du mouvement. De tels déplacements s'appellent des mouvements de convection. Ils sont à l'origine de certains phénomènes océanographiques (courants marins), météorologiques (orages), géologiques (remontées de magma) par exemple.

La convection thermique n'est pas le seul moyen de créer des mouvements verticaux dans des fluides. Ceux-ci vont se stratifier selon leur densité, à température uniforme, par l'effet de la gravité. Cette convection gravitationnelle se déroule comme la convection thermique avec les zones du fluide plus denses descendant et les parties moins denses poussées vers le haut. Cependant, il n'y a pas de variation de températures dans ces échanges. On peut citer la diffusion de la salinité dans une couche isothermale ou le déplacement du sel vers le bas dans une terre humide[1].

Dans un environnement à microgravité comme dans l'espace, la convection naturelle n'est pas possible puisque la poussée d'Archimède s'exerce par la différence de force gravitationnelle sur des volumes de densités différentes. Ainsi la circulation de la chaleur doit être forcée dans une capsule spatiale. Une flamme aurait également de la difficulté à exister car les gaz de combustion resteraient près de la flamme, la coupant de l'apport d'oxygène. Il faut pour l'entretenir une circulation forcée pour éloigner ces gaz et amener l'oxygène[2].

Une particule de fluide chauffée à la base devient moins dense du fait de sa dilatation thermique et remonte sous l'action de la poussée d'Archimède. Arrivée au sommet de la couche, le fluide échange sa chaleur, se refroidit et s'alourdit. Il redescend alors et crée un transfert retour de chaleur. La première approche physique a été mise en place par Henri Bénard, avec l'étude de la convection dans une couche de fluide soumise à un gradient de température vertical. Ces expériences sont connues sous le nom de cellules de Bénard.

Vie courante

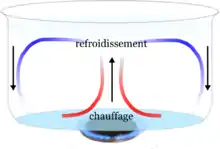
Présentation de la convection dans une casserole.

Le mouvement dans une casserole posée sur le feu s'explique par les différences de densité créées par le chauffage. Le fluide se met en mouvement spontanément, par convection naturelle, quand la différence de température entre le haut et le bas de la couche d'eau atteint une valeur critique.
La fumée de cigarette ou de cheminée monte car la combustion crée une zone très chaude et très peu dense par rapport à l'air environnant. Cette zone de fluide monte sous l'action de la poussée d'Archimède.
Le chauffage par le sol relève du même principe. La couche chaude à la base des pièces, du fait de la dilatation thermique, devient plus légère (relativement) et engendre une circulation dans la maison.
Le fonctionnement de la lampe à lave repose sur ce même phénomène : la cire est chauffée par le fond jusqu'à ce que sa densité soit inférieure à celle du fluide environnant. Elle s'élève alors en formant des panaches qui, une fois au sommet de la lampe, refroidissent et retombent au fond du récipient.
Dans le manteau terrestre, des courants de convection mantellique sont à l'origine des contraintes de compression et des contraintes d'expansion (selon leurs mouvements), ce qui cause la déformation des roches.
Pour l'isolation thermique d'une habitation, l'air enfermé entre la toiture et le plancher des combles, ou entre un mur porteur et un mur intérieur, n'assure aucunement l'isolation à cause du phénomène de convection accéléré par une différence de température entre paroi chaude et paroi froide. Pour réaliser l'isolation, il faut ajouter dans cet espace un matériau isolant dans lequel l'air enfermé dans des bulles ou entre des fibres ne peut pas participer à la convection.

Mise en équation du phénomène physique

Approche de la physique des milieux continus

Notation :

$\lambda$ désigne la conductivité thermique du fluide ;
$\rho$ désigne la masse volumique du fluide ;
$c_{p}$ désigne la capacité thermique massique du fluide ;
$T$ désigne la température du fluide ;
${\overrightarrow {u}}$ désigne la vitesse du fluide ;
${\overrightarrow {\varphi }}$ désigne la densité de flux thermique.

Hypothèses simplificatrices :

Propriétés ( $\lambda$ , $\rho$ , $c_{p}$ ) du fluide constantes.
Pas de changement de phase.
Milieu stationnaire.
Fluide incompressible.

La mise en équation de la diffusion de la chaleur (loi de Fourier) au sein du fluide aboutit à :

${\overrightarrow {\varphi }}_{dif}$ = $-\lambda$ ${\overrightarrow {\nabla }}$ $T$

La mise en équation de l'advection de la chaleur au sein du fluide aboutit à :

${\overrightarrow {\varphi }}_{adv}=\rho \,c_{p}T{\overrightarrow {u}}$

La densité de flux de chaleur par convection est la somme de la densité de flux de chaleur par diffusion et par advection, soit :

${\overrightarrow {\varphi }}_{conv}=-\lambda {\overrightarrow {\nabla }}T+\rho \,c_{p}T{\overrightarrow {u}}$

Le premier principe de la thermodynamique affirme que l'énergie se conserve, ce qui se traduit en équation par :

${\overrightarrow {\nabla }}\cdot {\overrightarrow {\varphi }}=-\rho \,c_{p}{\frac {\partial T}{\partial t}}$

Ce qui permet d'écrire l'équation d'advection-diffusion de la chaleur :

$\rho \,c_{p}{\frac {\partial T}{\partial t}}=-{\overrightarrow {\nabla }}\cdot \left(-\lambda {\overrightarrow {\nabla }}T+\rho \,c_{p}T{\overrightarrow {u}}\right)$

Puisqu'il a été supposé que le fluide est incompressible ${\overrightarrow {\nabla }}\cdot {\overrightarrow {u}}=0$ . Cela donne :

$\rho \,c_{p}{\frac {\partial T}{\partial t}}=\lambda \Delta T-\rho c_{p}\left({\overrightarrow {u}}\cdot {\overrightarrow {\nabla }}\right)T$

Les solutions de cette équation ne peuvent être trouvées que si le champ de vitesse est connue. Sinon il est nécessaire de résoudre, préalablement ou en parallèle, les équations de Navier-Stokes. C'est, entre autres, l'un des objectifs de la mécanique des fluides numérique.

Approche phénoménologique

Pour un écoulement à température $T_{\infty }$ autour d'une structure à température de surface uniforme $T_{\mathrm {S} }$ et d'aire $A$ , l'expression du flux de chaleur convectif $φ$ est donnée par la loi de Newton :

\varphi =hA(T_{\mathrm {S} }-T_{\infty })

où :

$φ$ est exprimé en watts (W) ;
$h$ est le coefficient de transfert thermique, en watts par mètre carré et par kelvin (W/m²/K, W⋅m⁻²⋅K⁻¹).

Pour une convection en air calme, dans des conditions normales de température et de pression, on a typiquement h compris entre 5 et 25 W m⁻² K⁻¹

L’existence de la fonction est connue, mais pas la fonction elle-même. De nombreuses études expérimentales ont permis d’identifier des corrélations empiriques s'approchant de la fonction reliant ces deux nombres. Ces corrélations sont souvent regroupées dans des abaques, utiles à l'ingénieur qui pourra ainsi déduire le coefficient de transfert thermique pour des configurations typiques.

Analyse adimensionnelle de la convection forcée

L'analyse dimensionnelle et l'application du théorème de Vaschy-Buckingham à un problème (simplifié) de convection forcée permet de montrer que seuls deux nombres adimensionnels suffisent pour décrire le problème. Conventionnellement, on utilise le nombre de Reynolds et le nombre de Nusselt :

$\mathrm {Re} ={\frac {\rho \,U\,L}{\mu }}$ , nombre de Reynolds
$\mathrm {Nu} ={\frac {h\,L}{\lambda }}$ , nombre de Nusselt

avec :

$\rho$ - masse volumique
$U$ - vitesse caractéristique du problème
$L$ - longueur caractéristique du problème
$\mu$ - viscosité dynamique
$\lambda$ - conductivité thermique

Le théorème de Vaschy-Buckingham affirme qu'il existe une fonction reliant ces deux nombres adimensionnels :

$\mathrm {Nu} =f(\mathrm {Re} )$

Analyse adimensionnelle de la convection naturelle/libre

L'analyse dimensionnelle et l'application du théorème de Vaschy-Buckingham à un problème (simplifié) de convection libre permet de montrer que seulement deux nombres adimensionnels suffisent pour décrire le problème. Conventionnellement on utilise le nombre de Rayleigh et le nombre de Nusselt :

$\mathrm {Ra} ={\frac {g\beta }{\nu \alpha }}(T_{\mathrm {s} }-T_{\infty }){L_{\mathrm {c} }}^{3}$
$\mathrm {Nu} ={\frac {h\,L}{\lambda }}$ , nombre de Nusselt ;

avec :

g - accélération de la pesanteur
L_c - longueur caractéristique
T_s - température de la paroi
T_∞ - température du fluide loin de la paroi
ν - viscosité cinématique
α - Diffusivité thermique
β - coefficient de dilatation thermique volumétrique

Le théorème de Vaschy-Buckingham affirme qu'il existe une fonction reliant ces deux nombres adimensionnels :

$\mathrm {Nu} =f(\mathrm {Ra} )$

Notes et références

Notes

Références

(en) P. A. C. Raats, « Steady Gravitational Convection Induced by a Line Source of Salt in a Soil », Soil Science Society of America Journal, n^o 33,‎ 1969, p. 483-487 (résumé)
(en) Cecil Adams, « If you lit a match in zero gravity, would it smother in its own smoke? », The Straight Dope (consulté le 22 mars 2008).

(en) Adrian Bejan, Convection Heat Transfer, John Wiley & Sons, 2013 (ISBN 978-1-118-33008-1)
(en) Oleg G. Martynenko et A. F. Polijakov, « Free Convection », sur Thermopedia
(en) A. V. Getling, « Rayleigh-Bénard convection », sur Scholarpedia

Articles connexes

Portail de la physique
Portail de l’énergie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) P. A. C. Raats, « Steady Gravitational Convection Induced by a Line Source of Salt in a Soil », Soil Science Society of America Journal, n^o 33,‎ 1969, p. 483-487 (résumé)

[2] (en) Cecil Adams, « If you lit a match in zero gravity, would it smother in its own smoke? », The Straight Dope (consulté le 22 mars 2008).